Графический метод
в задачах с параметром
Введение.
Я выбрала эту тему, так как она является неотъемлемой частью изучения школьного курса алгебры. Готовя данную работу, я ставила цель более глубокого изучения этой темы, выявления наиболее рационального решения, быстро приводящего к ответу. Мой реферат поможет понять применение графического метода решения уравнений с параметрами, узнать о происхождении, развитии этого метода.
В современной жизни изучение многих физических процессов и геометрических закономерностей часто приводит к решению задач с параметрами.
Для решения таких уравнений графический метод является весьма эффективным, когда нужно установить, сколько корней имеет уравнение в зависимости от параметра а.
Задачи с параметрами представляют чисто математический интерес, способствуют интеллектуальному развитию учащихся, служат хорошим материалом для отработки навыков. Они обладают диагностической ценностью, так как с помощью них можно проверить знание основных разделов математики, уровень математического и логического мышления, первоначальные навыки исследовательской деятельности и перспективные возможности успешного овладения курса математики в высших учебных заведениях.
В моём реферате рассмотрены часто встречающиеся типы заданий и, я надеюсь, что знания, полученные мной в процессе работы, помогут мне при сдаче школьных экзаменов, ведь уравнения с параметрами по праву считаются одними из самых сложных задач в курсе школьной математики. Именно такие задачи и попадают в список заданий на едином государственном экзамене ЕГЭ.
§1 Что такое параметр.
Толковый словарь определяет «параметр» как величину, характеризующую какое - нибудь основное свойство машины, устройства, системы или явления, процесса. (Ожегов С.И. , Шведова Н.Ю. Толковый словарь русского языка. Москва. 1999). Рассмотрение параметров - это всегда выбор. Покупая какую-то вещь, мы внимательно изучаем ее основные характеристики. Так, приобретая компьютер, мы обращаем внимание на следующие его параметры: производительность, габариты, состав комплектующих, цену и др. Перед выбором мы стоим и в различных жизненных ситуациях.
Что такое параметр в математике? Если вы вспомните некоторые основные уравнения (например, kx+l=0, ax²+bx+c=0), то обратите внимание, что при поиске их корней значения остальных переменных, входящих в уравнения, считаются фиксированными и заданными. Все разночтения в существующей литературе связаны с толкованием того, какими фиксированными и заданными могут быть эти значения остальных переменных.
Поскольку в школьных учебниках нет определения параметра, возьмем за основу следующий его простейший вариант.
Определение: параметром называется независимая переменная, значение которой в задаче считается заданным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству.
Независимость параметра заключается в его «неподчинении» свойствам, вытекающим из условия задачи. Например, из неотрицательности левой части уравнения |x|=a–1 не следует неотрицательность значений выражения a–1, и если a–1
§2 Что означает «решить задачу с параметром»
и основные типы задач с параметрами.
Естественно, это зависит от вопроса в задаче. Если, например, требуется решить уравнение, неравенство, их систему или совокупность, то это означает предъявить обоснованный ответ либо для любого значения параметра, либо для значения параметра, принадлежащего заранее оговоренному множеству.
Если же требуется найти значения параметра, при которых множество решений уравнения, неравенства и т. д. удовлетворяет объявленному условию, то, очевидно, решение задачи и состоит в поиске указанных значений параметра.
На ЕГЭ встречаются два типа задач с параметрами. Первый «для каждого значения параметра найти все решения некоторого уравнения или неравенства». Второй «найти все значения параметра, при каждом из которых решения уравнения или неравенства удовлетворяют заданным условиям».
И ответы в задачах этих двух типов различаются по существу. В задачах первого типа ответ выглядит так: перечисляются все возможные значения параметра и для каждого из этих значений записываются решения уравнения. В ответах второго типа задач с параметром перечисляются все значения параметра, при которых выполнены условия задачи.
§3 Основные способы решения задач с параметром.
Аналитический - способ прямого решения, повторяющего стандартные процедуры нахождения ответа в уравнении без параметров.
Графический - в зависимости от условия задачи рассматривается положение графика функции в системе координат.
Графический способ. В зависимости от того, какая роль параметру отведена в задаче, можно соответственно выделить два основных графических приёма:
первый – построение графика на координатной плоскости (х;у),
второй – построение графика на координатной плоскости на (х;а).
На плоскости (х;у) или (х;а) функция y=f(x;a) задаёт семейство кривых, зависящих от параметра а. Понятно, что каждое семейство f обладает определёнными свойствами. Нас же в первую очередь будет интересовать с помощью какого преобразования плоскости (параллельный перенос, поворот и т.д.) можно перейти от одной прямой к какой-нибудь другой.
Если уравнение одной из фигур не зависит от изменяющегося параметра, то график этой фигуры неподвижен относительно системы координат. Если в уравнение другой фигуры входит параметр, то от его изменения зависит расположение и даже форма графика. Тогда суть решения уравнения состоит в определении числа точек пересечения графиков построенных уравнений, а значит в определении количества возможных решений в зависимости от конкретных числовых значений параметра.
Графический способ определения числа корней уравнения в зависимости от входящего в него параметра является более удобным, чем аналитический.
§4. «Базовые элементы» для решения задач с параметрами
Понятие функции — одно из ключевых в математике.
И конечно, в задачах части 2 Профильного ЕГЭ по математике без них не обойтись.
Математические функции, изучением которых мы занимаемся, — это не что-то такое выдуманное или существующее только в замкнутом пространстве учебника. Они являются отражением реальных взаимосвязей и процессов, происходящих в природе и обществе.
Существует всего пять типов элементарных функций:
1. Степенные
К этому типу относятся линейные, квадратичные, кубические,
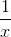 ,
,  ,
, 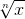 Все они содержат выражения вида xα.
Все они содержат выражения вида xα.
2. Показательные
Это функции вида y = ax
3. Логарифмические
y = logax.
4. Тригонометрические
В их формулах присутствуют синусы, косинусы, тангенсы и котангенсы.
5. Обратные тригонометрические
Содержат arcsinx, arccosx, arctgx, arcctgx.
Элементарными они называются потому, что из них, как из элементов, получаются все остальные, встречающиеся в школьном курсе. Например, y = x2 · ex — произведение квадратичной и показательной функций; y = sin(ax) — сложная функция, то есть комбинация двух функций — показательной и тригонометрической.
В задачах с параметрами Профильного ЕГЭ по математике встречаются не только графики функций (в школьном смысле этого слова), но и множества точек на плоскости.
Вот несколько уравнений и неравенств, задающих окружность, круг, ромбик, отрезок. Заметим, что окружность или ромбик, хотя и задаются уравнениями, не являются графиками функций в школьном смысле этого слова.
Задачи с параметрами на ЕГЭ по математике считаются одними из самых сложных. Однако на самом деле они похожи на конструктор, где вы собираете решение из готовых элементов. Чтобы уверенно решать задачи с параметрами, необходимо отлично знать типы элементарных функций и их графики. Преобразования графиков функций. И вот эти базовые элементы:
1. Уравнение 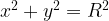 задает окружность с центром в начале координат и радиусом
задает окружность с центром в начале координат и радиусом 
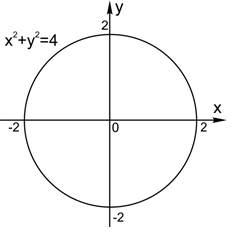
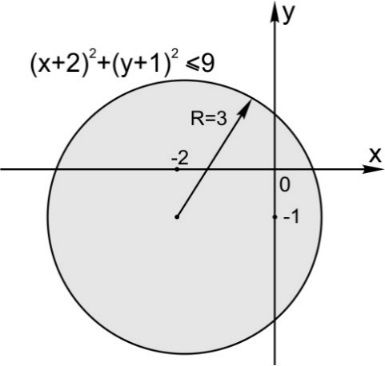
2. Уравнение  задает окружность с центром в точке (a;b) и радиусом
задает окружность с центром в точке (a;b) и радиусом 

3. Неравенство  задает круг вместе с границей
задает круг вместе с границей
4. Уравнение 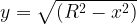 задает верхнюю полуокружность с центром в начале координат и радиусом
задает верхнюю полуокружность с центром в начале координат и радиусом 

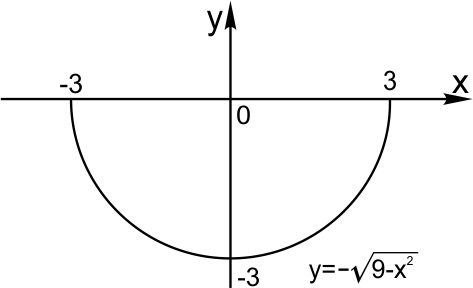
5. Уравнение 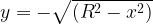 задает нижнюю полуокружность с центром в начале координат и радиусом
задает нижнюю полуокружность с центром в начале координат и радиусом 
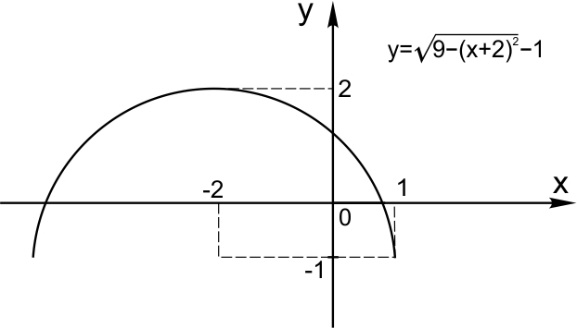
6. Уравнение 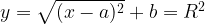 задает верхнюю полуокружность центром в точке
задает верхнюю полуокружность центром в точке  и радиусом
и радиусом 
7. Уравнение 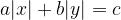 при положительных
при положительных 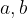 и
и  задает ромбик, симметричный относительно начала координат.
задает ромбик, симметричный относительно начала координат.

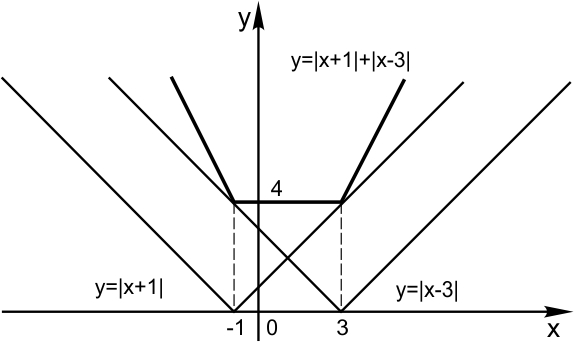
8. Уравнение 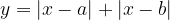 (сумма модулей) задает график следующего вида:
(сумма модулей) задает график следующего вида:
§5 Преобразование графиков функций
В своей работе я рассмотрела основные преобразованиях графиков функций. Что нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали. Как задать растяжение графика по горизонтали или вертикали. Как отразить график относительно оси Х или Y.
Эта тема - полезная и очень интересная — выпадает из школьной программы. Для того, чтобы решать задачи с параметрами, стоит научиться строить графики функций.
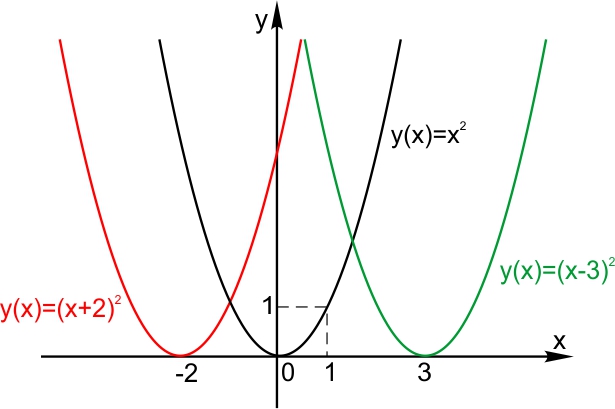
Начнем со сдвигов графиков по Х и по Y.
Сдвиг по горизонтали.
Пусть функция задана формулой 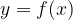 и
и  Тогда график функции
Тогда график функции 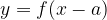 сдвинут относительно исходной на а вправо. График функции
сдвинут относительно исходной на а вправо. График функции 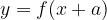 сдвинут относительно исходной на а влево.
сдвинут относительно исходной на а влево.
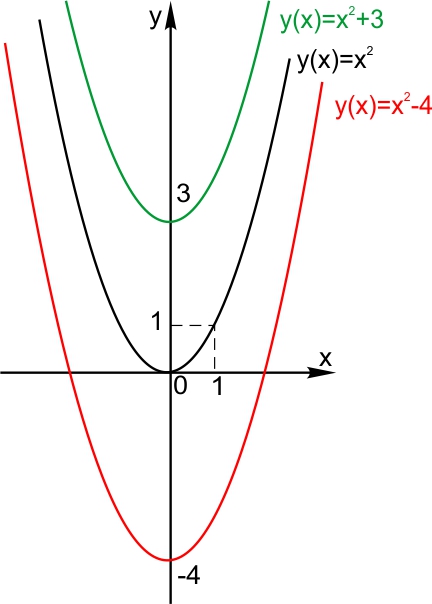
Сдвиг по вертикали.
Пусть функция задана формулой 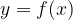 и С — некоторое положительное число. Тогда график функции
и С — некоторое положительное число. Тогда график функции  сдвинут относительно исходного на С вверх. График функции
сдвинут относительно исходного на С вверх. График функции 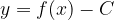 сдвинут относительно исходного на С вниз.
сдвинут относительно исходного на С вниз.
Теперь растяжение графика или сжатие.
Растяжение (сжатие) по горизонтали.
Пусть функция задана формулой 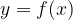 и
и 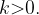 Тогда график функции
Тогда график функции  растянут относительно исходного в k раз по горизонтали, если
растянут относительно исходного в k раз по горизонтали, если  , и сжат относительно исходного в k раз по горизонтали, если
, и сжат относительно исходного в k раз по горизонтали, если 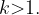

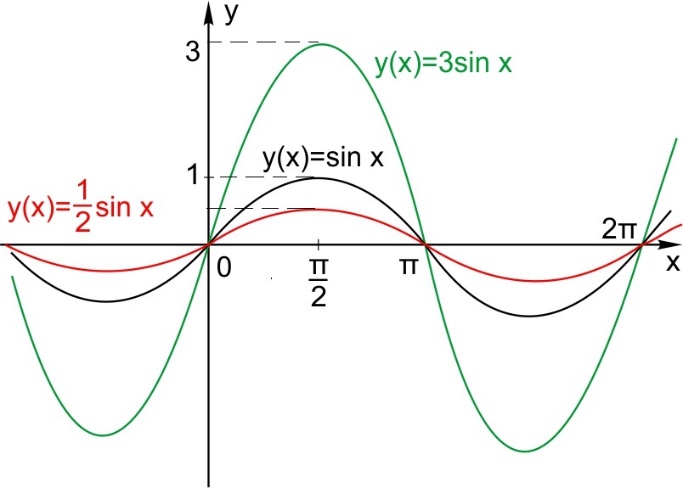
Растяжение (сжатие) по вертикали
Пусть функция задана формулой 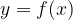 и
и 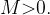 Тогда график функции
Тогда график функции 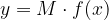 растянут относительно исходного в М раз по вертикали, если
растянут относительно исходного в М раз по вертикали, если  , и сжат относительно исходного в М раз по вертикали, если
, и сжат относительно исходного в М раз по вертикали, если 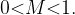
Отражение по горизонтали.
График функции 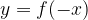 симметричен графику функции
симметричен графику функции 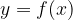 относительно оси Y.
относительно оси Y.

Отражение по вертикали.
График функции 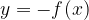 симметричен графику функции
симметричен графику функции 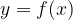 относительно оси Х.
относительно оси Х.
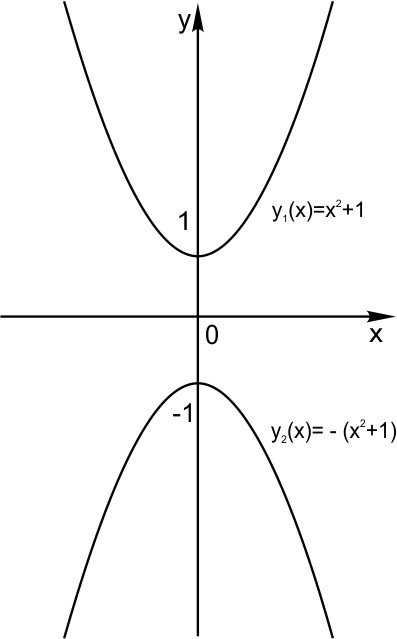
И еще два интересных преобразования.
Здесь в формулах присутствует знак модуля
Графики функций 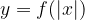 и
и 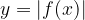
На рисунке изображен график функции  Она специально взята такая — несимметричная относительно нуля.
Она специально взята такая — несимметричная относительно нуля.
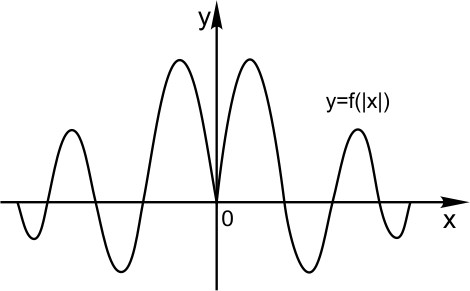
Построим график функции 
Конечно же, мы пользуемся определением модуля.

Это мы и видим на графике. Для неотрицательных значений х график остался таким же, как был. А вместо каждого отрицательного х мы взяли противоположное ему положительное число. И поэтому вся та часть графика функции, что лежала слева от оси Х, заменилась на зеркально отраженную правую часть графика.
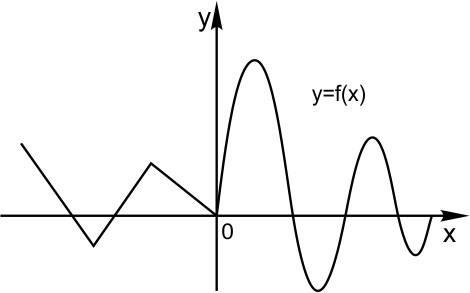
Теперь график функции  Вся часть графика, лежащая ниже оси Х, зеркально отражается в верхнюю полуплоскость. А верхняя часть графика, лежащая выше оси Х, остается на месте.
Вся часть графика, лежащая ниже оси Х, зеркально отражается в верхнюю полуплоскость. А верхняя часть графика, лежащая выше оси Х, остается на месте.
Как определить по формуле функции, будет график преобразован по горизонтали (по Х) или по вертикали (по Y)? Разница очевидна. Если сначала мы что-либо делаем с аргументом х (прибавляем к нему какое-либо число, умножаем на какое-либо число или берем модуль) — преобразование по Х. Если сначала мы нашли функцию, а затем уже к значению функции что-то прибавили, или на какое-нибудь число умножили, или взяли модуль, - преобразование по Y.
§6. Решение задач.
Задача 1. Сколько корней имеет уравнение | | x | – 2 | = a в зависимости от параметра a?
Решение. В системе координат (x; y) построим графики функций y = | | x | – 2 | и y = a. График функции y = | | x | – 2 | изображен на рисунке.
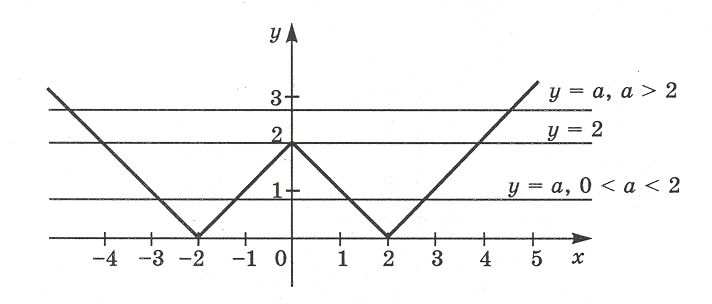
Графиком функции y = а является прямая, параллельная оси Ox или с ней совпадающая (при a = 0).
Из графика видно, что:
Если a = 0, то прямая y = a совпадает с осью Ox и имеет с графиком функции y = | | x | – 2 | две общие точки; значит, исходное уравнение имеет два корня (в данном случае корни можно найти: x1,2 = + 2).
Если 0 a Если a = 2, то прямая y = 2 имеет с графиком функции три общие точки. Тогда исходное уравнение имеет три корня.
Если a 2, то прямая y = a будет иметь с графиком исходной функции две точки, то есть данное уравнение будет иметь два корня.
Ответ: если a если a = 0, a 2, то два корня;
если a = 2, то три корня;
если 0 a
Задача 2. Сколько корней имеет уравнение | x2 – 2| x | – 3 | = a в зависимости от параметра a?
Решение. В системе координат (x; y) построим графики функций
y = | x2 – 2| x | – 3 | и y = a.
График функции y = | x2 – 2| x | – 3 | изображен на рисунке. Графиком функции y = a является прямая, параллельная Ox или с ней совпадающая (когда a = 0).
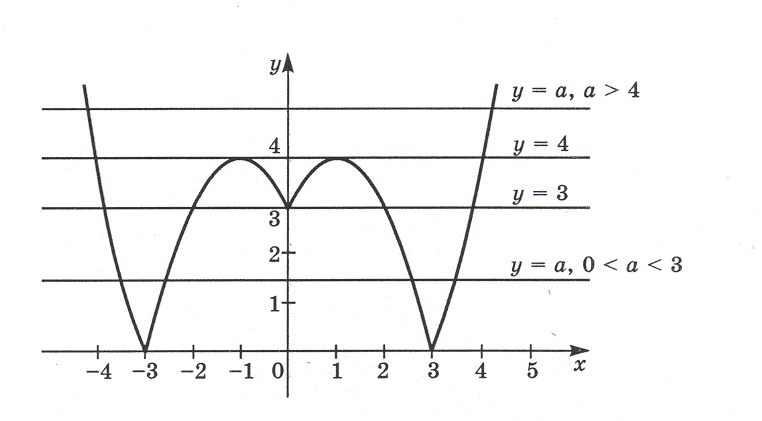
Из графика видно:
Если a = 0, то прямая y = a совпадает с осью Ox и имеет с графиком функции
y = | x2 – 2| x | – 3 | две общие точки, а также прямая y = a будет иметь с графиком функции y = | x2 – 2| x | – 3 | две общие точки при a 4. Значит, при a = 0 и a 4 исходное уравнение имеет два корня.
Если 0 a a имеет с графиком функции y = | x2 – 2| x | – 3 | четыре общие точки, а также прямая y=a будет иметь с графиком построенной функции четыре общие точки при a = 4. Значит, при 0 a a = 4 исходное уравнение имеет четыре корня.
Если a = 3, то прямая y = a пересекает график функции в пяти точках; следовательно, уравнение имеет пять корней.
Если 3 a Если a 2 – 2| x | – 3 |.
Ответ: если a если a = 0, a 4, то два корня;
если 0 a a = 4, то четыре корня;
если a = 3, то пять корней;
если 3 a
Задача 3. Найдите все значения а, при каждом из которых решения неравенства 
 образуют отрезок длины 1.
образуют отрезок длины 1.
Решение. Перенесем единицу: 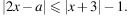

Построим графики функций 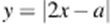 и
и 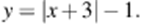

На рисунке видно, что неравенство имеет решения только при 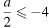 или
или 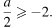

1)
Решения образуют отрезок длины 1, если 
 откуда
откуда 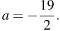
2) 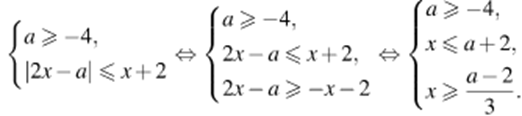
Решения образуют отрезок длины 1, если 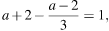
 откуда
откуда 
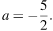

Ответ: 
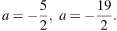

Задача 4. Сколько корней имеет уравнение
x + 2 = a | x – 1 |
в зависимости от параметра a?
Решение. Заметим, что x = 1 не является корнем данного уравнения, так как равенство 3 = a0 не может быть верным ни при каком значении параметра a. Разделим обе части уравнения на | x – 1 |(| x – 1 | 0), тогда уравнение примет вид 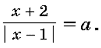 В системе координат xOy построим график функции
В системе координат xOy построим график функции 

График этой функции изображен на рисунке. Графиком функции y = a является прямая, параллельная оси Ox или с ней совпадающая (при a = 0).
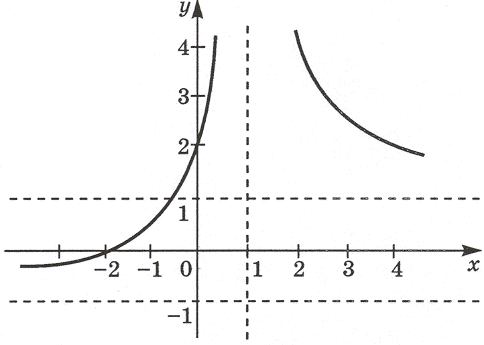
Далее рассуждая так же, как и в предыдущей задаче, получаем ответ.
Ответ: если a – 1, то корней нет;
если – 1 a 1, то один корень;
если a 1, то два корня.
Задача 5. При каких значениях параметра a уравнение
ax2 + | x – 1 | = 0 имеет три решения?
Решение. 1. Контрольным значением параметра для данного уравнения будет число a = 0, при котором уравнение примет вид 0 + | x – 1 | = 0, откуда x = 1. Следовательно, при a = 0 уравнение имеет один корень, что не удовлетворяет условию задачи.
2.Рассмотрим случай, когда a ax2 = – | x – 1 |. Заметим, что уравнение будет иметь решения только при a
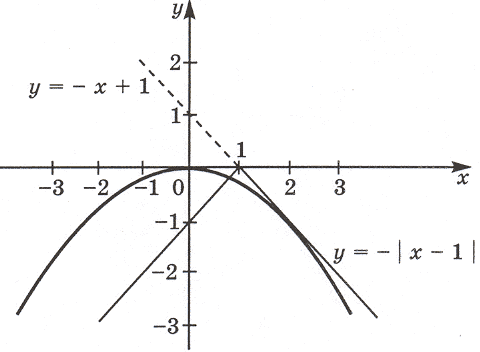
В системе координат xOy построим графики функций y = | x – 1 | и y = ax2. График функции y = | x – 1 | изображен на рисунке. Графиком функции y = ax2 является парабола, ветви которой направлены вниз, так как a
Уравнение будет иметь три решения только тогда, когда прямая y = – x + 1 будет касательной к графику функции y=ax2.
Пусть x0 — абсцисса точки касания прямой y = – x + 1 с параболой y = ax2. Уравнение касательной имеет вид
y = y(x0) + y '(x0)(x – x0).
Запишем условия касания:
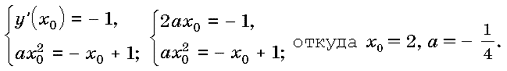
Данное уравнение можно решить без использования понятия производной.
Рассмотрим другой способ. Воспользуемся тем, что если прямая y = kx + b имеет единственную общую точку с параболой y = ax2 + px + q, то уравнение ax2 + px + q = kx + b должно иметь единственное решение, то есть его дискриминант равен нулю. В нашем случае имеем уравнение ax2 = – x + 1 (a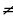 0). Дискриминант уравнения
0). Дискриминант уравнения 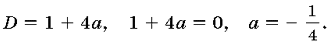
Ответ: 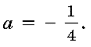
Задача 6. Найдите все значения 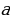 , при каждом из которых система неравенств
, при каждом из которых система неравенств 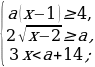 имеет хотя бы одно решение на отрезке [4; 5].
имеет хотя бы одно решение на отрезке [4; 5].
Преобразуем систему: 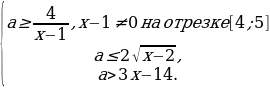
Построим прямоугольную систему координат xOa. Изобразим множество точек, координаты которых удовлетворяют системе неравенств.
Гипербола  и график корня
и график корня  пересекаются в точке N(3; 2). Гипербола и прямая
пересекаются в точке N(3; 2). Гипербола и прямая 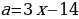 пересекаются в точке M(5; 1). График корня и прямая пересекаются в точке K(6; 4). Множество точек, координаты которых удовлетворяют заданной системе состоит из точек криволинейного треугольника NMK, не включая границу, лежащую на прямой КМ.
пересекаются в точке M(5; 1). График корня и прямая пересекаются в точке K(6; 4). Множество точек, координаты которых удовлетворяют заданной системе состоит из точек криволинейного треугольника NMK, не включая границу, лежащую на прямой КМ.
Поскольку система должна иметь хотя бы одно решение на отрезке [4; 5], определим наименьшую и наибольшую ординаты проекции выделенного на рисунке четырехугольника на ось ординат.
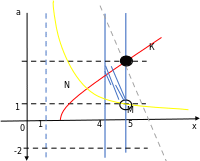
Найдём координаты точки P:
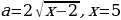 =
=
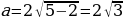
Проекции точек P и M дают искомое множество: заданная система неравенств имеет хотя бы одно решение на отрезке [4; 5] при  (выделено штриховкой на рисунке).
(выделено штриховкой на рисунке).
Ответ: (1; 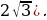
Задача 7. Найдите все значения а, при каждом из которых уравнение 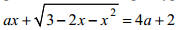 имеет единственный корень.
имеет единственный корень.
Запишем уравнение в виде  и рассмотрим две функции
и рассмотрим две функции 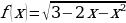 и
и 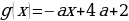 .
.
Рассмотрим функцию 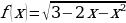 , преобразовывая подкоренное выражение, получим:
, преобразовывая подкоренное выражение, получим:
 .
.
Таким образом, получаем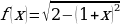 .функцию, графиком которой является полуокружность с радиусом 2 в центре с точкой (-1;0), лежащей в верхней полуплоскости.
.функцию, графиком которой является полуокружность с радиусом 2 в центре с точкой (-1;0), лежащей в верхней полуплоскости.
Г рафиком функции
рафиком функции 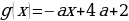 является прямая с угловым коэффициентом -а, проходящая через точку М (4;2)
является прямая с угловым коэффициентом -а, проходящая через точку М (4;2)
Уравнение имеет единственный корень, если графики функций имеют одну общую точку (т.е. прямая касается или пересекает полуокружность в единственной точке).
Рассмотрим рисунок: 1. Прямая МС является касательной к полуокружности, следовательно, МС и полуокружность пересекаются в единственной точке. Так как МС параллельна оси ОХ ( У точки М (4,2) и С(-1,2)), то угловой коэффициент 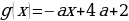 равен нулю. Таким образом, найдено первое значение а=0, при котором уравнение имеет один единственный корень.
равен нулю. Таким образом, найдено первое значение а=0, при котором уравнение имеет один единственный корень.
2. Проведем прямую через точки М(4;2) и А(-3;0) ( так как координаты известны). Прямая МА пересекает график полуокружности в двух точках, но такая ситуация не удовлетворяет условию задачи. Поэтому надо найти значения углового коэффициента, при которых вышеназванное условие не выполняется. Чтобы найти значения –а подставим координаты точек М и А в функцию 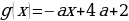 .
.
-4а+16а+2=2 3а+4а+2=0
12а=0 7а=-2
а=0. а=
Получаем, -а=0 и –а=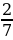 .
.
При условии 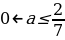 прямые имеют с графиком две общие точки, а это не удовлетворяет условию задачи.
прямые имеют с графиком две общие точки, а это не удовлетворяет условию задачи.
3. Проведем прямую МВ через точки М(4;2) и В(1;0). Чтобы найти значения –а подставим координаты точек М и А в функцию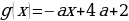 .
.
3а+4а+2=0 -а+4а+2=0
7а=-2 3а=-2
а= а =
а =
Получаем –а= и –а=
и –а=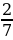 . При условии
. При условии 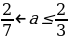 прямые имеют с графиком одну общие точки и это удовлетворяет условию задачи.
прямые имеют с графиком одну общие точки и это удовлетворяет условию задачи.
Ответ: а=0, 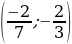
Задача 8. Найдите все значения 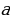 , для каждого из которых уравнение
, для каждого из которых уравнение
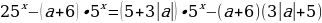
имеет единственное решение.
Аналитический способ:
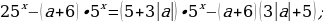
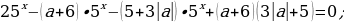
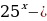 ;
;
Пусть 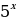 = t 0, тогда:
= t 0, тогда:
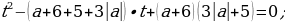 (*)
(*)
Исходное уравнение будет иметь единственное решение:
1 случай: еcли уравнение (*) имеет единственное решение (D=0);
2 случай: если уравнение (*) имеет два корня (D0), один из которых меньше нуля или равен нулю.
Пусть n=a+6, m=5+3|a|;
1 случай:
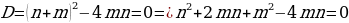 =
=  =
= 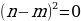 =
= 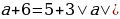 =
=  ;
;
если a 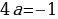 =
= 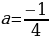 ; если a0, то
; если a0, то  =
= 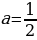 .
.
2 случай:
 ;
;  ;
;
если nm, то:
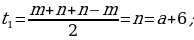
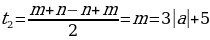 ;
;
если n
 ;
; 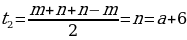 ;
;
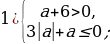
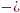 система не имеет решений, т.к. выражение 3|a|+5 всегда положительно.
система не имеет решений, т.к. выражение 3|a|+5 всегда положительно.
 =
= 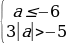 =
=
или 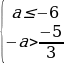 =
= 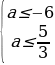 =
= 
или 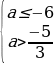 =
= 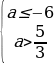 = система не имеет решений.
= система не имеет решений.
Ответ: 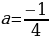 ;
; 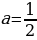 ;
;  .
.
Графический способ:
Преобразуем исходное уравнение:
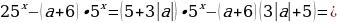
 =
=
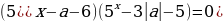 =
= 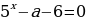 или
или 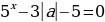 .
.
Построим графики функций 
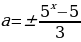 на координатной плоскости xOa:
на координатной плоскости xOa:
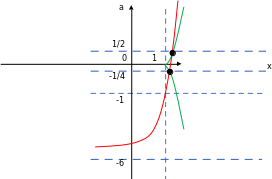
На чертеже заметим, что система имеет единственное решение при 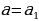 ,
, 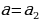 и
и  . Найдём
. Найдём  и
и 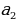 :
:
Если a0, то: 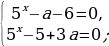 =
= 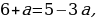 =
=  .
.
Если а 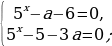 =
= 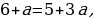 =
=  .
.
Ответ: 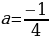 ;
; 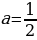 ;
;  .
.
Задача 9. Найдите все значения 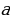 , при каждом из которых имеет ровно три различных решения система уравнений
, при каждом из которых имеет ровно три различных решения система уравнений 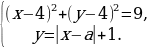
Первое уравнение системы является уравнением окружности с центром в точке 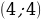 и радиусом 3. График функции
и радиусом 3. График функции  получается параллельным переносом на вектор
получается параллельным переносом на вектор 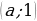 графика функции
графика функции 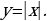 Поскольку график функции
Поскольку график функции  представляет собой прямой угол с вершиной в точке
представляет собой прямой угол с вершиной в точке 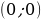 и сторонами лежащими на прямых
и сторонами лежащими на прямых 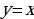 и
и 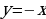 выше оси абсцисс, график функции
выше оси абсцисс, график функции  также представляет собой прямой угол, но с вершиной в точке
также представляет собой прямой угол, но с вершиной в точке 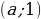 и сторонами, параллельными прямым
и сторонами, параллельными прямым  Заметим, что прямая
Заметим, что прямая 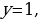 на которой лежит вершина угла, является касательной к окружности.
на которой лежит вершина угла, является касательной к окружности.

Ровно три общие точки фигуры имеют в следующих случаях:
1. Вершина прямого угла лежит в точке 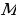 касания окружности и прямой
касания окружности и прямой  , а его стороны пересекают окружность в двух точках (первый случай). Это возможно, только если
, а его стороны пересекают окружность в двух точках (первый случай). Это возможно, только если 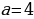 .
.
2. Одна из сторон прямого угла пересекает окружность в двух точках, а другая касается окружности в точке 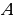 (второй случай) или в точке
(второй случай) или в точке 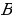 (третий случай). Найдём значения параметра для этих двух случаев. Поскольку радиус окружности, проведённый в точку касания окружности и прямой, перпендикулярен прямой, четырёхугольник
(третий случай). Найдём значения параметра для этих двух случаев. Поскольку радиус окружности, проведённый в точку касания окружности и прямой, перпендикулярен прямой, четырёхугольник  является квадратом со стороной
является квадратом со стороной 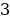 и диагональю
и диагональю  . Тогда
. Тогда  . Следовательно, для случая касания в точке
. Следовательно, для случая касания в точке 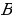 получаем
получаем 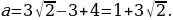 Для касания стороны угла и окружности в точке
Для касания стороны угла и окружности в точке 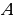 аналогично получаем ещё одно значение параметра:
аналогично получаем ещё одно значение параметра: 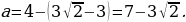
При 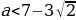 или
или 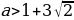 прямой угол имеет не более двух общих точек с окружностью.
прямой угол имеет не более двух общих точек с окружностью.
При 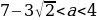 или
или 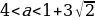 прямой угол имеет четыре общие точки с окружностью.
прямой угол имеет четыре общие точки с окружностью.
Ответ: 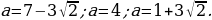
 Задача 10. Найдите все значения параметра а, при каждом из которых система уравнений имеет ровно 4 решения.
Задача 10. Найдите все значения параметра а, при каждом из которых система уравнений имеет ровно 4 решения.
П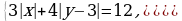 реобразуем данную систему:
реобразуем данную систему:
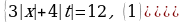
Пусть t = y – 3, тогда система примет вид:
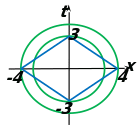
Количество решений полученной системы совпадает с количеством решений исходной системы.
Построим графики уравнений (1) и (2) в системе координат Oxt. График первого уравнения – ромб, диагонали которого, равные 8 и 6, лежат на осях Ох и Оt, а графиком второго уравнения является окружность с центром в начале координат и радиусом r = |a|.
С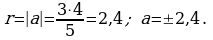 истема имеет 4 решения, так как графики уравнений системы пересекаются в четырех общих точках. Значит, окружность либо вписана в ромб, либо ее радиус удовлетворяет условию 3
истема имеет 4 решения, так как графики уравнений системы пересекаются в четырех общих точках. Значит, окружность либо вписана в ромб, либо ее радиус удовлетворяет условию 3
Во втором случае получаем 3 |a |
Ответ: а = ± 2,4; −4
Заключение
Работая над это темой, я провела большую работу: изучила литературу по выбранной теме; разобралась, что такое параметр и задачи с параметрами; познакомилась с методами их решения.
Выполняя практическую часть, было решено много уравнений, неравенств и их систем, я приобрела опыт и научилась решать определённый круг задач и пришла к некоторым выводам.
Решение каждого задания требует к себе индивидуального подхода, но при этом задачи с параметрами чем-то похожи на детский конструктор. Разобрав много таких примеров, можно заметить, как решение «собирается» из мелких деталей – хорошо знакомых нам фактов.
Для себя я выделила два основных способа решения №17 из ЕГЭ:
аналитический и графический.
Графический способ является наиболее наглядным, простым и доступным способом решения задач с параметрами. Если задачу с параметром можно нарисовать – рисуем. То есть применяем графический метод. Размытость в решение уравнения, неравенства или их системы с помощью графика, можно подкрепить аналитическим выводом, что поможет подтвердить правоту выбранного решения и ответа.
Сочетание аналитического способа решения с графической интерпретацией полученных результатов позволяет сделать процесс решения уравнений с параметрами более осознанным, способствуя при этом формированию элементов исследовательской деятельности.
Мне эта работа интересна.
Задачи с параметрами помогают в формировании логического мышления, в приобретении навыков исследовательской деятельности. Возможность и умение решать задачи с параметрами демонстрируют владение методами решения уравнений и неравенств, осмысленное понимание теоретических сведений, уровень логического мышления, стимулируют познавательную деятельность.
Список литературы
1.Корянов А.Г., Прокофьев А.А. Уравнения и неравенства с параметрами. Количество решений.
2.Шарыгин И.Ф., В.И.Голубев. Факультативный курс по математике. Решение задач. Учебное пособие для 11 класса. Москва «Просвещение». 1991 г.
3.Моденов В.П. Задачи с параметрами Москва «Экзамен» 2017
Интернет – ресурсы:
http://reshuege.ru "Решу ЕГЭ" - образовательный портал
https://egemaximum.ru/category/17/
https://ege-study.ru/graficheskij-metod-resheniya-zadach-s-parametrami/
34
























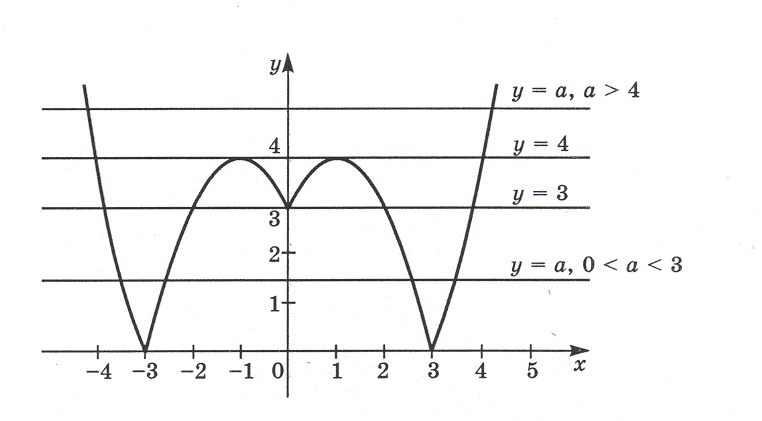
 образуют отрезок длины 1.
образуют отрезок длины 1.

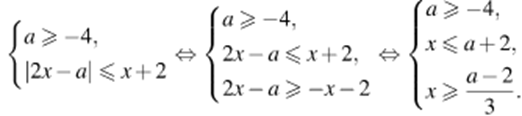



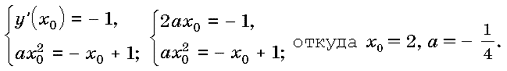
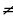 0). Дискриминант уравнения
0). Дискриминант уравнения 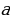 , при каждом из которых система неравенств
, при каждом из которых система неравенств 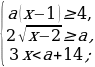 имеет хотя бы одно решение на отрезке [4; 5].
имеет хотя бы одно решение на отрезке [4; 5].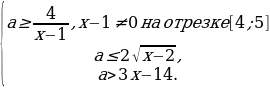
 и график корня
и график корня  пересекаются в точке N(3; 2). Гипербола и прямая
пересекаются в точке N(3; 2). Гипербола и прямая 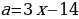 пересекаются в точке M(5; 1). График корня и прямая пересекаются в точке K(6; 4). Множество точек, координаты которых удовлетворяют заданной системе состоит из точек криволинейного треугольника NMK, не включая границу, лежащую на прямой КМ.
пересекаются в точке M(5; 1). График корня и прямая пересекаются в точке K(6; 4). Множество точек, координаты которых удовлетворяют заданной системе состоит из точек криволинейного треугольника NMK, не включая границу, лежащую на прямой КМ.
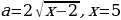 =
=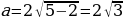
 (выделено штриховкой на рисунке).
(выделено штриховкой на рисунке).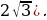
 и рассмотрим две функции
и рассмотрим две функции 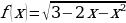 и
и 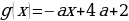 .
. .
. 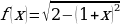 .функцию, графиком которой является полуокружность с радиусом 2 в центре с точкой (-1;0), лежащей в верхней полуплоскости.
.функцию, графиком которой является полуокружность с радиусом 2 в центре с точкой (-1;0), лежащей в верхней полуплоскости. рафиком функции
рафиком функции 
 .
. 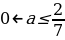 прямые имеют с графиком две общие точки, а это не удовлетворяет условию задачи.
прямые имеют с графиком две общие точки, а это не удовлетворяет условию задачи. 
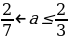 прямые имеют с графиком одну общие точки и это удовлетворяет условию задачи.
прямые имеют с графиком одну общие точки и это удовлетворяет условию задачи.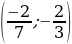
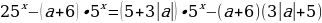
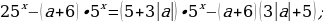
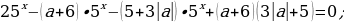
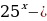 ;
;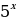 = t 0, тогда:
= t 0, тогда: 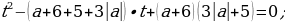 (*)
(*)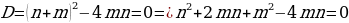 =
=  =
= 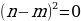 =
= 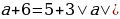 =
=  ;
;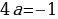 =
= 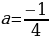 ; если a0, то
; если a0, то  =
= 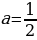 .
. ;
;  ;
;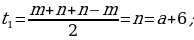
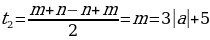 ;
; ;
; 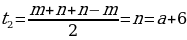 ;
;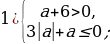
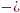 система не имеет решений, т.к. выражение 3|a|+5 всегда положительно.
система не имеет решений, т.к. выражение 3|a|+5 всегда положительно.  =
= 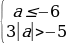 =
=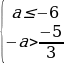 =
= 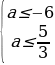 =
= 
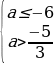 =
= 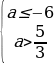 = система не имеет решений.
= система не имеет решений. 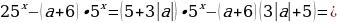
 =
=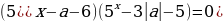 =
= 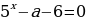 или
или 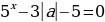 .
.
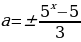 на координатной плоскости xOa:
на координатной плоскости xOa: 
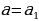 ,
, 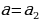 и
и  и
и 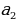 :
: 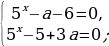 =
= 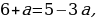 =
=  .
.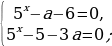 =
= 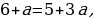 =
=  .
.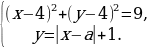
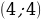 и радиусом 3. График функции
и радиусом 3. График функции  получается параллельным переносом на вектор
получается параллельным переносом на вектор 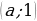 графика функции
графика функции 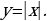 Поскольку график функции
Поскольку график функции  представляет собой прямой угол с вершиной в точке
представляет собой прямой угол с вершиной в точке 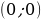 и сторонами лежащими на прямых
и сторонами лежащими на прямых 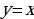 и
и 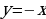 выше оси абсцисс, график функции
выше оси абсцисс, график функции 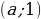 и сторонами, параллельными прямым
и сторонами, параллельными прямым  Заметим, что прямая
Заметим, что прямая 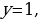 на которой лежит вершина угла, является касательной к окружности.
на которой лежит вершина угла, является касательной к окружности.
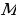 касания окружности и прямой
касания окружности и прямой  , а его стороны пересекают окружность в двух точках (первый случай). Это возможно, только если
, а его стороны пересекают окружность в двух точках (первый случай). Это возможно, только если 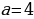 .
. 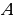 (второй случай) или в точке
(второй случай) или в точке 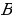 (третий случай). Найдём значения параметра для этих двух случаев. Поскольку радиус окружности, проведённый в точку касания окружности и прямой, перпендикулярен прямой, четырёхугольник
(третий случай). Найдём значения параметра для этих двух случаев. Поскольку радиус окружности, проведённый в точку касания окружности и прямой, перпендикулярен прямой, четырёхугольник  является квадратом со стороной
является квадратом со стороной 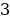 и диагональю
и диагональю  . Тогда
. Тогда  . Следовательно, для случая касания в точке
. Следовательно, для случая касания в точке 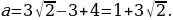 Для касания стороны угла и окружности в точке
Для касания стороны угла и окружности в точке 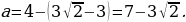
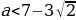 или
или 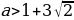 прямой угол имеет не более двух общих точек с окружностью.
прямой угол имеет не более двух общих точек с окружностью.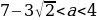 или
или 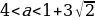 прямой угол имеет четыре общие точки с окружностью.
прямой угол имеет четыре общие точки с окружностью. 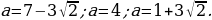
 Задача 10. Найдите все значения параметра а, при каждом из которых система уравнений имеет ровно 4 решения.
Задача 10. Найдите все значения параметра а, при каждом из которых система уравнений имеет ровно 4 решения.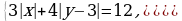 реобразуем данную систему:
реобразуем данную систему: 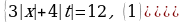

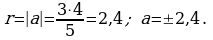 истема имеет 4 решения, так как графики уравнений системы пересекаются в четырех общих точках. Значит, окружность либо вписана в ромб, либо ее радиус удовлетворяет условию 3
истема имеет 4 решения, так как графики уравнений системы пересекаются в четырех общих точках. Значит, окружность либо вписана в ромб, либо ее радиус удовлетворяет условию 3 
















