
Мультимедийное учебное пособие Графические методы решения задач с параметрами
Авторы: Сунгатуллина Малика Наилевна
Ибрагимова Альфия Рустемовна,
Научный руководитель: Гайнанова Мадина Газизовна, учитель высшей категории
МБОУ «Гимназия №7» г. Казани.

Изучению функций и их свойств посвящена значительная часть курса алгебры. Понятие функции имеет огромное прикладное значение. Они широко используются при изучении, как курса математики, так и других школьных предметов, находят широкое применение в практической деятельности человека.

Цель работы :
рассмотрение преобразования графиков элементарных функций, изучение алгоритма решения задач графическим методом.

Задачи работы :
- Систематизировать и обобщить знания по преобразованию графиков;
- изучить функционально-графический, координатно-параметрический методы и метод областей;
- разобрать примеры применения графических методов при решении различных задач;
- создать электронное учебное пособие для изучения преобразований графиков и алгоритмов решения задач с параметрами графическим методом и проверить его эффективность в учебном эксперименте .

Преобразования графиков.
Построение графиков функций и уравнений вида:
у=f(-x)
y=f(x)+m
у=|f(x)|
у=f(x+n)
у=kf(x)
у=f(|x|)
у=f(bx)
|у|=f(x)
у=-f(x)
 0, и на |А| единиц вниз, если А = = y cos x -3 = y cos x + 3 y cos x y 1 O x -1 список Следующее преобразование другой пример " width="640"
0, и на |А| единиц вниз, если А = = y cos x -3 = y cos x + 3 y cos x y 1 O x -1 список Следующее преобразование другой пример " width="640"
Сдвиг вдоль оси ординат Преобразование у =f(х) → у =f(х)+А Параллельный перенос графика функции у =f(х) вдоль оси ОУ на А единиц вверх, если А0, и на |А| единиц вниз, если А
=
=
y
cos x -3
=
y
cos x + 3
y
cos x
y
1
O
x
-1
список
Следующее преобразование
другой пример

y
y = x 2
y = x 2 +3
y = x 2 -3
x
1
0
Следующее преобразование
список
 0, и на |а| единиц вправо, если а x 0 1 y = x 2 y = (x-2) 2 y = (x+2) 2 Следующее преобразование список " width="640"
0, и на |а| единиц вправо, если а x 0 1 y = x 2 y = (x-2) 2 y = (x+2) 2 Следующее преобразование список " width="640"
y
Сдвиг вдоль оси абсцисс
Преобразование у =f(х) → у =f(х+ а)
Параллельный перенос графика функции у =f(х) вдоль оси ОХ на а единиц влево, если а 0, и на |а| единиц вправо, если а
x
0
1
y = x 2
y = (x-2) 2
y = (x+2) 2
Следующее преобразование
список
 0, k≠1). Растяжение графика функции у =f(х) вдоль оси ОУ от оси ОХ в k раз, если к 1, и сжатие в 1/k раз вдоль оси ОУ к оси ОХ, если 0 y = cos x y = 0,5cos x y = 1,5cos x y 1 O x -1 Следующее преобразование список подробнее " width="640"
0, k≠1). Растяжение графика функции у =f(х) вдоль оси ОУ от оси ОХ в k раз, если к 1, и сжатие в 1/k раз вдоль оси ОУ к оси ОХ, если 0 y = cos x y = 0,5cos x y = 1,5cos x y 1 O x -1 Следующее преобразование список подробнее " width="640"
Растяжение и сжатие вдоль оси ординат
Преобразование у =f(х) →
у = k f(х) (k 0, k≠1).
Растяжение графика функции у =f(х) вдоль оси ОУ от оси ОХ в k раз, если
к 1, и сжатие в 1/k раз вдоль оси ОУ к оси ОХ, если 0
y = cos x
y = 0,5cos x
y = 1,5cos x
y
1
O
x
-1
Следующее преобразование
список
подробнее

y
y = 1,5cos x
1
O
x
-1
y = cos x
y
1
O
x
-1
y = 0,5cos x
Следующее преобразование
список
 0, k≠1). Сжатие графика функции у =f(х) вдоль оси ОХ к оси ОУ в k раз, если k1, и растяжение в 1/k раз вдоль оси ОХ от оси ОУ, если 0 список " width="640"
0, k≠1). Сжатие графика функции у =f(х) вдоль оси ОХ к оси ОУ в k раз, если k1, и растяжение в 1/k раз вдоль оси ОХ от оси ОУ, если 0 список " width="640"
Растяжение и сжатие вдоль оси абсцисс
Преобразование у = f(х) →
у = f(k х)
( k 0, k≠1).
Сжатие графика функции у =f(х) вдоль оси ОХ к оси ОУ в k раз, если k1, и растяжение в 1/k раз вдоль оси ОХ от оси ОУ, если
0
список

y
y = cos 2x
x
O
y = cos x
y
x
O
y = cos 0,5x
Следующее преобразование
список

Симметричное отражение относительно оси абсцисс
y
Преобразование у = f(х) → у = - f(х).
Симметричное отражение графика функции у =f(х) относительно оси ОХ
x
0
1
Следующее преобразование
список

y
Симметричное отражение относительно оси ординат
Преобразование
у = f(х) → у = f(-х).
Симметричное отражение графика функции у =f(х) относительно оси ОУ
x
1
0
Следующее преобразование
список

Модуль функции
Преобразование у = f(х) → у =|f(х)|.
Часть графика, расположенная ниже оси ОХ, симметрично отражается относительно оси ОХ, остальная часть остается без изменений
y
O
x
1
-1
Следующее преобразование
список
другой пример

y
x
1
0
y = x 2 -4
| |
Следующее преобразование
список

y
Модуль аргумента
Преобразование у = f(х) →
у =f(|х|).
Часть графика у = f(х), расположенная левее оси ОУ исчезает, а расположенная правее оси ОУ остается без изменений, включая точку на оси, правая часть симметрично отражается относительно оси ОУ налево
x
1
0
| |
y = x 2 - 4 x +3
Следующее преобразование
список

| у| =f(х).
Преобразование у = f(х) →
| у| =f(х).
Часть графика у = f(х),
расположенная ниже
оси ОХ исчезает, а распо-
ложенная выше оси ОХ,
остается без изменений,
включая точку на оси,
верхняя часть симметрично
отражается относительно
оси ОХ в нижнюю
полуплоскость
х
x
0
1
| |
y = x 2 -4
список
![Семейства линий Уравнение F(x, у, а) = 0 при каждом фиксированном значении параметра а задает на плоскости XOY линию. При изменении параметра а получают множество линий, которое называется семейством линий [1].](https://fsd.multiurok.ru/html/2017/06/10/s_593c1db406cfa/img18.jpg)
Семейства линий
Уравнение F(x, у, а) = 0 при каждом фиксированном значении параметра а задает на плоскости XOY линию. При изменении параметра а получают множество линий, которое называется семейством линий [1].

Примеры семейств
Семейство окружностей
Семейство прямых y = kx
Семейство парабол y = kx 2
Семейство парабол y = (x+a) 2
Семейство окружностей (x+3) 2 +(y-a) = 4

Семейство
окружностей
x 2 +y 2 =R 2
x
0
1
список

y
Семейство прямых
y=kx
x
1
0
список

y
Семейство парабол
y = kx 2
k≠0
x
1
0
список
пропустить

(x+3) 2 +(y-a)=4
y
x
0
1
список
x
0
1
y = (x+a) 2
список
Функционально-графический метод решения задач с параметрами

Алгоритм решения в общем виде
- Уравнение приводится к виду f(x)=g(x;а) или f(x)
- Строятся графики левой и правой части уравнения или неравенства.
- По полученному графику «считывается» нужная информация.

Простейшие задачи с параметрами

1.1 Определите при каком значении параметра а система уравнений x 2 +(y+2) 2 =4,
y=|x|+a имеет а) 1 решение; б) 3 решения; в) 2 решения.
Ответ: а) 0; б)-4; в) (-4;0) U 2+2
Решение
1.2 Определите, при каком значении параметра а система уравнений
x 2 +у 2 =9
у=-х 2 +a имеет а) 1 решение; б) 3 решения.
Решение
Ответ: а)-3; б)3.
1.3 Определите при каком значении а данное уравнение
имеет 5 корней.
Ответ:-4
Решение

y
x 2 +(y+2) 2 =4
y=|x|+a
x
1
0
задачи

y
x 2 +(y+2) 2 =4
y=|x|+a
x
0
1
а) 1 решение;
б) 3 решения;
в) 2 решения.
задачи

O
задачи

y
х 2 +у 2 =9
у=-х 2 +a
x
1
0
задачи

y
х 2 +у 2 =9
у=-х 2 +a
x
1
0
а) 1 решение;
Ответ: а)-3;
б) 3 решения.
б) 3
задачи

Найдите всезначения a при которых данное уравнение
имеет 5 корней.
Рассмотрим два графика
парабола галочка
Подсказка
График
Решение
Ответ: -4
Ответ
задачи

Задачи повышенной сложности
 а – х не имеет решений [1]. 1.5 При каких значениях параметра а данное уравнение имеет единственный корень 1.6 При каком значении параметра а уравнение a = | -6|x|+3| имеет а) 4 корня; б) 8 корней? Ответ: a Решение Решение Ответ: -2 Решение Ответ: а) 0; 6; б) (0; 3). " width="640"
а – х не имеет решений [1]. 1.5 При каких значениях параметра а данное уравнение имеет единственный корень 1.6 При каком значении параметра а уравнение a = | -6|x|+3| имеет а) 4 корня; б) 8 корней? Ответ: a Решение Решение Ответ: -2 Решение Ответ: а) 0; 6; б) (0; 3). " width="640"
1.4 При каких значениях параметра а неравенство
а – х не имеет решений [1].
1.5 При каких значениях параметра а данное уравнение
имеет единственный корень
1.6 При каком значении параметра а уравнение
a = | -6|x|+3| имеет а) 4 корня; б) 8 корней?
Ответ: a
Решение
Решение
Ответ: -2
Решение
Ответ: а) 0; 6; б) (0; 3).
 неравенство не имеет решений. Ответ: а задачи " width="640"
неравенство не имеет решений. Ответ: а задачи " width="640"
4. При каких значениях параметра а неравенство не имеет решений.
Решение. Рассмотрим функции у =и у = а – х. Поскольку уравнение у =равносильно системе
графиком первой функции является полуокружность. Графиком функции у= а – х является семейство прямых, параллельных прямой у = -х. Условие задачи выполняется в тех случаях, когда нет точек полуокружности, расположенных выше соответствующих точек прямой. По графику можно определить, что при анеравенство не имеет решений.
Ответ: а
задачи

y
у = а – х
x
0
1
задачи
 a ϵ(-∞;-2] Рассмотрим два графика галочка, вершины которой имеют координаты (-а;а+2) Подсказка График Решение Ответ Ответ: (-∞;-2] задачи " width="640"
a ϵ(-∞;-2] Рассмотрим два графика галочка, вершины которой имеют координаты (-а;а+2) Подсказка График Решение Ответ Ответ: (-∞;-2] задачи " width="640"
Найдите всезначения a при которых данное уравнение
имеет единственный корень.
(-a ;)=
a ϵ(-∞;-2]
Рассмотрим два графика
галочка, вершины
которой имеют
координаты (-а;а+2)
Подсказка
График
Решение
Ответ
Ответ: (-∞;-2]
задачи

y
6.При каком значении параметра а уравнение a = |x 2 -6|x|+3 | имеет
а) 4 корня; б) 8 корней?
Построим графики функций
| |
| |
y = x 2 -6 x +3
и
x
у=а
1
0
задачи

y
x
0
1
Ответ: а) 0 и 6
б) (0;3)
задачи

Трудные задачи

7. Семенов А. Л., Ященко И.В. Типовые тестовые задания ЕГЭ. Вар.3,С5.
Найти все значения а, при каждом из которых система
(х+3) 2 + (у-9) 2 =25
y = |х-а|+4 имеет три различных решения.
8. А.Л. Семенов, И.В. Ященко. Типовые тестовые задания.2013 год. Вар.7, С5.
При каких значениях параметра а уравнение | x 2 -4х-5|-3а=|х-а|-1 имеет ровно три корня?
9. А.Л.Семенов,И.В. Ященко. Типовые тестовые задания.2013 год. Вар. 15, С5.
Найти все значения параметра а, при каждом из которых система уравнений имеет ровно четыре решения.
Решение
Ответ: о или
Решение
Ответ: -0,25; -0,125.
Решение
№ 10,11

10. ЕГЭ 2013 года, задача С5.
Найдите все значения а, при каждом из которых уравнение
ax + =4a+2 имеет единственный корень.
11. Найдите все значения параметра а, при которых уравнение
имеет единственный корень
Решение
Ответ: (-2 ; +∞)
Решение

y
(х+3) 2 + (у-9) 2 =25
y = |х-а|+4
O
0
1
x
задачи

y
(х+3) 2 + (у-9) 2 =25
y = |х-а|+4
O
0
1
x
задачи

y
O
К
А
Т
В
С
Р
-3
0
1
x
задачи

задачи

y
у= |х 2 -4х-5| ; у=|х-а|+3а-1
0
1
x
задачи

y
А
0
1
x
задачи

y
у = -х 2 +4х+5
0
1
x
задачи

1)Левая сторона угла (прямая у =|х-а|+3а-1=а-х+3а-1=4а-х-1) касается параболы
у = - х 2 +4х+5, т. е., уравнение
– х 2 +4х+5=4а-х-1 имеет единственный корень. Упростим его: – х 2 +5х+6 - 4а=0.
D=49 - 16а.
D=0 при
задачи

2)Левая сторона угла, т. е., прямая у=а-х+3а-1 проходит через точку А(-1;0). Тогда выполняется равенство: а+1+3а-1=0, откуда а=0.
Ответ: 0 и
задачи

Задача. Найти все значения параметра а, при каждом из которых система уравнений
имеет ровно 4 решения.
Решение: Введем новые переменные: х-1=m, 7у=n. Тогда система примет вид:
Графиком 1 уравнения в системе координат (m,n) является квадрат c вершинами (1;0), 0;1), (-1;0), (0;-1), а 2 уравнения – окружность с центром в начале координат и радиусом , , где а ≤ 0
задачи

Графики имеют ровно 4 точки пересечения в 2 случаях:
1)Окружность описана около квадрата, т. е., R=1. Тогда =1, откуда а = .
2)Окружность вписана в квадрат, тогда R = , т.е., = ;
а = .
n
m
1
Ответ: ;
задачи

Найдите все значения а , при каждом из которых уравнение ax + =4a+2 имеет единственный корень.
Решение: ах + =4а+2
Приведем к виду = -ах+4а+2. Рассмотрим две функции: у = и у=-ах+4а+2.
1) y = 3–2x–x 2
y 2 =3-2x-x 2 , где y 0
y 2 +x 2 +2x-3=0
y 2 +(x 2 +2x+1)=4
y 2 +(x+1) 2 =2 2
Графиком уравнения является
полуокружность с центром
в точке (0; -1), R =2.
2)y= –ax+4a+2
y= - a(x-4)+2.
Графиком функции является семейство прямых, проходящих через точку (4; 2).
задачи
![y x 0 1 4 Условие задачи выполняется, если а=0, или точка пересечения данной прямой с осью Х находится в промежутке ( -3; 1]. y 2 +(x+1) 2 =2 2 , y= - a(x+4)+2 где y 0 задачи](https://fsd.multiurok.ru/html/2017/06/10/s_593c1db406cfa/img57.jpg)
y
x
0
1
4
Условие задачи выполняется, если а=0, или точка пересечения данной прямой с осью Х находится в промежутке
( -3; 1].
y 2 +(x+1) 2 =2 2 ,
y= - a(x+4)+2
где y 0
задачи

задачи

задачи

Найдите всезначения a при которых данное уравнение
имеет 1 корень
Подсказка
Рассмотрим два графика
График
Решение
Ответ
Ответ: (- ∞ ;4 )
задачи

Задачи для самопроверки
Задача 1
Задача 2

о
Рассмотрим два графика
Подсказка
График
Решение
Ответ
Ответ: 0; (2; + ∞ )
задачи

Найдите всезначения a при которых данное уравнение
имеет 5 корней.
Подсказка
График
Решение
Ответ
Ответ: 3
задачи

Координатно-параметрический метод решения задач с параметрами
![Иногда параметр удобно рассматривать как полноценную переменную, аргумент или функцию. Тогда одна из осей будет координатной, а другая называется параметрической, а координатная плоскость – координатно-параметрической. Данный способ основан на нахождении множества всех точек координатно-параметрической плоскости, значения координаты и параметра а каждой из которых удовлетворяют заданному в условиях задачи соотношению. Этот метод называется координатно-параметрическим и впервые был применен преподавателем МГУ В.П. Моденовым более тридцати лет назад [2].](https://fsd.multiurok.ru/html/2017/06/10/s_593c1db406cfa/img65.jpg)
Иногда параметр удобно рассматривать как полноценную переменную, аргумент или функцию. Тогда одна из осей будет координатной, а другая называется параметрической, а координатная плоскость – координатно-параметрической. Данный способ основан на нахождении множества всех точек координатно-параметрической плоскости, значения координаты и параметра а каждой из которых удовлетворяют заданному в условиях задачи соотношению.
Этот метод называется координатно-параметрическим и впервые был применен преподавателем МГУ В.П. Моденовым более тридцати лет назад [2].
![х 2 +a 2 =4, a=|x| 2.1 При каких значениях параметра а система имеет 2 решения? 2.2 При каких значениях параметра уравнение |2x+3|+|2x-3|= ах + 6 имеет более двух корней [4]. 2.3 Найти все значения параметра а, при каждом из которых уравнение (а+4х-х 2 -1)(а + 1-|x-2|)=0 имеет ровно три корня [1]. Ответ: Решение Ответ: 0. Решение Ответ:-1 Решение 6](https://fsd.multiurok.ru/html/2017/06/10/s_593c1db406cfa/img66.jpg)
х 2 +a 2 =4,
a=|x|
2.1 При каких значениях параметра а система
имеет 2 решения?
2.2 При каких значениях параметра уравнение |2x+3|+|2x-3|= ах + 6 имеет более двух корней [4].
2.3 Найти все значения параметра а, при каждом из которых уравнение (а+4х-х 2 -1)(а + 1-|x-2|)=0 имеет ровно три корня [1].
Ответ:
Решение
Ответ: 0.
Решение
Ответ:-1
Решение
6

2.1 При каких значениях параметра а система
имеет 2 решения?
Решение: Построим множество решений данной
системы уравнений на плоскости (а; х).
Окружность и «уголок» пересекаются в 2 точках
при а =
Ответ:
задачи
6

2.2 При каких значениях параметра а уравнение имеет более двух корней
Решение . При х = 0 получим 6 = 6, что означает, что число 0 является корнем уравнения при любом х.
При х ≠ 0, уравнение примет вид:
а =
Раскрыв модули в каждом промежутке, получим:
а =
задачи

Построим в плоскости (х, а) точки, координаты которых удовлетворяют полученным уравнениям. По графику можно определить, что условие задачи выполняется, если а = 0.
а
1
х
Ответ: а = 0.
задачи

2.3 Найти все значения параметра а, при каждом из которых уравнение (а+4х-х 2 -1)(а+1-|x-2|)=0 имеет ровно три корня
a
Решение:Приведем к виду:
a = х 2 -4х+1,
a=|x-2|-1.
Графиком этой совокупности
является объединение «уголка»
и параболы.
Очевидно, что лишь
прямая a=-1 пересекает данное
объединение в трех точках.
Ответ: a=-1.
1
x
-1
задачи

Метод областей
 0. Пусть уравнение Р(х;у)=0 задает некоторые линии на плоскости. Разобьем этими линиями координатную плоскость на конечное число областей G 1, G 2, …G i , ограниченных линиями Р=0 Теорема: В каждой из областей G i, на которые линии Р(х;у)=0 делят координатную плоскость, многочлен Р(х; у) либо положителен, либо отрицателен. Таким образом, решение неравенства Р(х;у)0 - множество всех пар (х;у), при которых неравенство выполняется, образует объединение тех областей G i , в которых значение многочлена Р(х;у) положительно. Для определения знака многочлена в областях достаточно определить знак в любой точке из этой области [2]. " width="640"
0. Пусть уравнение Р(х;у)=0 задает некоторые линии на плоскости. Разобьем этими линиями координатную плоскость на конечное число областей G 1, G 2, …G i , ограниченных линиями Р=0 Теорема: В каждой из областей G i, на которые линии Р(х;у)=0 делят координатную плоскость, многочлен Р(х; у) либо положителен, либо отрицателен. Таким образом, решение неравенства Р(х;у)0 - множество всех пар (х;у), при которых неравенство выполняется, образует объединение тех областей G i , в которых значение многочлена Р(х;у) положительно. Для определения знака многочлена в областях достаточно определить знак в любой точке из этой области [2]. " width="640"
Рассмотрим неравенство Р(х;у)0.
Пусть уравнение Р(х;у)=0 задает некоторые линии на плоскости. Разобьем этими линиями координатную плоскость на конечное число областей G 1, G 2, …G i , ограниченных линиями Р=0
Теорема: В каждой из областей G i, на которые линии Р(х;у)=0 делят координатную плоскость, многочлен Р(х; у) либо положителен, либо отрицателен.
Таким образом, решение неравенства Р(х;у)0 - множество всех пар (х;у), при которых неравенство выполняется, образует объединение тех областей G i , в которых значение многочлена Р(х;у) положительно.
Для определения знака многочлена в областях достаточно определить знак в любой точке из этой области [2].
 0. Алгоритм Найти на КП-плоскости ОДЗ. Построить на КП-плоскости линии, состоящие из точек, в которых Р(х;а)=0 или не существует. Определить знаки выражения Р(х;а) в каждой из областей (для этого достаточно установить знак выражения в какой-нибудь точке области). Найти ответ. " width="640"
0. Алгоритм Найти на КП-плоскости ОДЗ. Построить на КП-плоскости линии, состоящие из точек, в которых Р(х;а)=0 или не существует. Определить знаки выражения Р(х;а) в каждой из областей (для этого достаточно установить знак выражения в какой-нибудь точке области). Найти ответ. " width="640"
Аналогично применяется метод областей и для КП-плоскости, при решении неравенства вида Р(х; а) 0.
Алгоритм
- Найти на КП-плоскости ОДЗ.
- Построить на КП-плоскости линии, состоящие из точек, в которых Р(х;а)=0 или не существует.
- Определить знаки выражения Р(х;а) в каждой из областей (для этого достаточно установить знак выражения в какой-нибудь точке области).
- Найти ответ.
![3.1 Изобразите множество точек, координаты которых удовлетворяют неравенству (х-у)(ху-1)≤0 на координатной плоскости 3.2 Изобразите множество точек, координаты которых удовлетворяют на координатной плоскости неравенству 0 [9]. 3.3 А. Л. Семенов, И. В. Ященко. Типовые тестовые задания.2013 год. Вар. 5, С5 . Найти все значения параметра а, при каждом из которых система неравенств не имеет решения. 3.4 А. Л. Семенов, И. В. Ященко. Типовые тестовые задания.2014 год. Вар. 2, С5 . Найти все значения параметра а, при каждом из которых неравенство | | имеет единственное решение на отрезке [ 1;3 ] Решение Решение Решение Решение](https://fsd.multiurok.ru/html/2017/06/10/s_593c1db406cfa/img74.jpg)
3.1 Изобразите множество точек, координаты которых удовлетворяют неравенству (х-у)(ху-1)≤0 на координатной плоскости
3.2 Изобразите множество точек, координаты которых удовлетворяют на координатной плоскости неравенству
0 [9].
3.3 А. Л. Семенов, И. В. Ященко. Типовые тестовые задания.2013 год. Вар. 5, С5 .
Найти все значения параметра а, при каждом из которых система неравенств
не имеет решения.
3.4 А. Л. Семенов, И. В. Ященко. Типовые тестовые задания.2014 год. Вар. 2, С5 .
Найти все значения параметра а, при каждом из которых неравенство | | имеет единственное решение на отрезке [ 1;3 ]
Решение
Решение
Решение
Решение

3.1 Изобразите множество точек, координаты которых удовлетворяют неравенству (х-у)(ху-1)≤0 на координатной плоскости.
Решение:
Найдем уравнения «граничных» линий: (х-у)(ху-1)=0,
Построим «граничные» линии, которые разбивают координатную плоскость на несколько областей. Определим знак выражения (х-у)(ху-1) в одной области, подставив в нее координаты произвольной точки из этой области. Например, в области, содержащей точку (0;1), получится знак +, и т. д.
задачи

у
-
+
+
1
х
-
-
+
задачи

3.2 Изобразите множество точек, координаты которых удовлетворяют на координатной плоскости неравенству
ноон
задачи

у
-
+
+
+
-
-
1
х
+
-
задачи

3.3 А. Л. Семенов, И. В. Ященко. Типовые тестовые задания.
2013 год. Вар. 5, С5
Найти все значения параметра а , при каждом из которых система неравенств
не имеет решений.
Решение:
1)х-а=0 и ах-2а-3=0
2)построим в системе координат (а ; х) графики функций х = а и х = 2 +
Расставим знаки в этих областях, определив координаты в отдельных точках каждой области. Решением первого неравенства являются координаты точек из областей со знаком + .
задачи

Х = а
х
+
-
-
-2
1
+
0
а
+
-
задачи

3)Решением второго неравенства является координаты точек,
расположенных выше правой
ветви гиперболы х =
и ниже левой ее ветви.
x
-2
а
0
задачи

4) Найдем решение системы, т. е., пересечение двух множеств.
5) По графику можно определить, что система не имеет решений при значениях параметра -2 0.
задачи
![Х = а х + - - -2 0 а + + - Ответ: (-2;0] задачи](https://fsd.multiurok.ru/html/2017/06/10/s_593c1db406cfa/img83.jpg)
Х = а
х
+
-
-
-2
0
а
+
+
-
Ответ: (-2;0]
задачи
![3.4 А. Л. Семенов, И. В. Ященко. Типовые тестовые задания.2014 год. Вар. 2, С5 . Найти все значения параметра а, при каждом из которых неравенство | | имеет единственное решение на отрезке [ 1;3 ] Решение: Приведем к виду: . ОДЗ: х ≠а |х 2 -2х-а| |2х-2а|; 0; (х 2 -2х-а+2х-2а)(х 2 -2х-а-2х+2а) 0; (х 2 -3а)(х 2 -4х+а) 0; (*) Решим методом областей. Решением уравнения (х 2 -3а)(х 2 -4х+а=0 является объединение двух парабол: а= х 2 и а=4х-х 2 , которые разбивают координатную плоскость на 5 областей. Расставим знаки левой части неравенства (*) в полученных областях. задачи](https://fsd.multiurok.ru/html/2017/06/10/s_593c1db406cfa/img84.jpg)
3.4 А. Л. Семенов, И. В. Ященко. Типовые тестовые задания.2014 год. Вар. 2, С5 .
Найти все значения параметра а, при каждом из которых неравенство | | имеет единственное решение на отрезке [ 1;3 ]
Решение: Приведем к виду: .
ОДЗ: х ≠а
|х 2 -2х-а| |2х-2а|;
0;
(х 2 -2х-а+2х-2а)(х 2 -2х-а-2х+2а) 0;
(х 2 -3а)(х 2 -4х+а) 0; (*)
Решим методом областей. Решением уравнения (х 2 -3а)(х 2 -4х+а=0 является объединение двух парабол:
а= х 2 и а=4х-х 2 , которые разбивают координатную плоскость на 5 областей.
Расставим знаки левой части неравенства (*) в полученных областях.
задачи
![a a ≠х а=4х- х 2 a = По графику можно опреде лить, что неравенство имеет единственное решение на отрезке[1; 3] при а=3. Ответ: 3 - + a =3. + x 0 1 + - задачи](https://fsd.multiurok.ru/html/2017/06/10/s_593c1db406cfa/img85.jpg)
a
a ≠х
а=4х-
х 2
a =
По графику можно опреде
лить, что неравенство имеет
единственное решение
на отрезке[1; 3]
при а=3.
Ответ: 3
-
+
a =3.
+
x
0
1
+
-
задачи

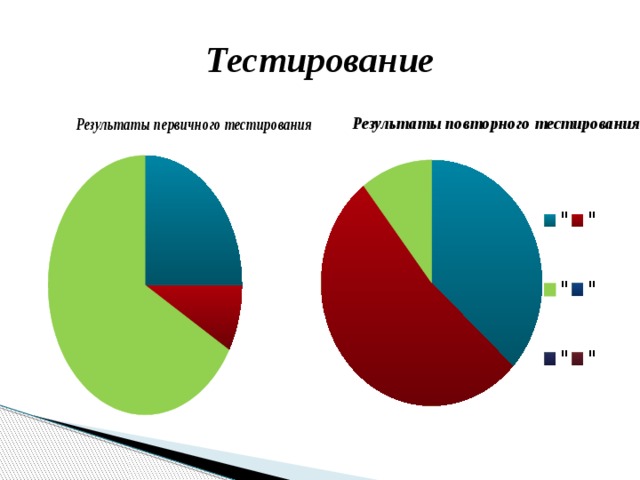
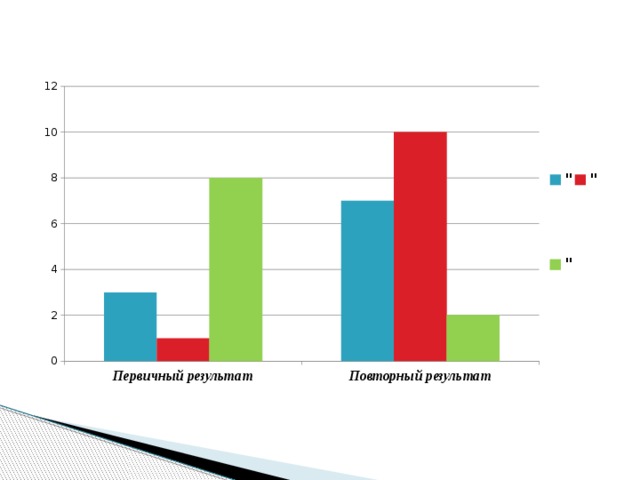
Тестирование


Выполняя эту работу, мы хотели обосновать
возможности графического способа решения уравнений с
параметрами. Рациональность любого верного решения
опирается на условия задачи и напрямую зависит от них.
Иногда графический метод помогает наиболее быстро и
удобно решить задачу, но не стоит забывать, что не все
решения можно увидеть. Графический способ сам по себе не
позволяет найти точные решения, поэтому при решении
задач подобным способом не обойтись без аналитических
формул и вычислений.
Данное пособие предназначено для учащихся выпускных
классов как помощь в самоподготовке. Надеемся, что она
также будет полезна и для учителей.
Литература.
- Горнштейн П.И., Полонский В.Б., Якир М.С. Задачи с параметрами. «Илекса», «Гимназия», Москва – Харьков, 2002.
- В. П. Моденов. Задания с параметрами. Координатно-параметрический метод. «Экзамен» 2007 г.
- Панферов В.С., Сергеев И.Н. Отличник ЕГЭ. Математика. Решение сложных задач; ФИПИ – М.: Интеллект-Центр, 2010.
- Прокофьев А.А. Задачи с параметрами. Учебное пособие. – М.: МИЭТ, 2004.
- www.mathege.ru – Математика ЕГЭ 2012, 2013 (открытый банк заданий).
- www.alexlarin. narod.ru – сайт по оказанию информационной поддержки студентам и абитуриентам при подготовке к ЕГЭ.
- Корянов А.Г., Прокофьев А.А. Использование метода наглядной графической интерпретации при решении уравнений и неравенств с параметрами. // Математика в школе. 2011. №1. – стр. 18-26.и 2011. №2. – стр. 25-32.
- http://gym1.ucoz.ru - сайт гимназии №1 Полярные зори Мурманской области. Мастерская. Мультимедийные презентации к уроку.
- В.С. Высоцкий. – Задачи с параметрами при подготовке к ЕГЭ, 2011 г. Москва, Научный мир.
- Математика. Типовые тестовые задания. – Под редакцией А. Л. Семенова, И. В. Ященко. Издательство «Экзамен», Москва, 2014 г.
- Математика. Типовые тестовые задания. – Под редакцией А. Л. Семенова, И. В. Ященко. Издательство «Экзамен», Москва, 2013 г.

Спасибо за внимание!










 0, и на |А| единиц вниз, если А = = y cos x -3 = y cos x + 3 y cos x y 1 O x -1 список Следующее преобразование другой пример " width="640"
0, и на |А| единиц вниз, если А = = y cos x -3 = y cos x + 3 y cos x y 1 O x -1 список Следующее преобразование другой пример " width="640"

 0, и на |а| единиц вправо, если а x 0 1 y = x 2 y = (x-2) 2 y = (x+2) 2 Следующее преобразование список " width="640"
0, и на |а| единиц вправо, если а x 0 1 y = x 2 y = (x-2) 2 y = (x+2) 2 Следующее преобразование список " width="640"
 0, k≠1). Растяжение графика функции у =f(х) вдоль оси ОУ от оси ОХ в k раз, если к 1, и сжатие в 1/k раз вдоль оси ОУ к оси ОХ, если 0 y = cos x y = 0,5cos x y = 1,5cos x y 1 O x -1 Следующее преобразование список подробнее " width="640"
0, k≠1). Растяжение графика функции у =f(х) вдоль оси ОУ от оси ОХ в k раз, если к 1, и сжатие в 1/k раз вдоль оси ОУ к оси ОХ, если 0 y = cos x y = 0,5cos x y = 1,5cos x y 1 O x -1 Следующее преобразование список подробнее " width="640"

 0, k≠1). Сжатие графика функции у =f(х) вдоль оси ОХ к оси ОУ в k раз, если k1, и растяжение в 1/k раз вдоль оси ОХ от оси ОУ, если 0 список " width="640"
0, k≠1). Сжатие графика функции у =f(х) вдоль оси ОХ к оси ОУ в k раз, если k1, и растяжение в 1/k раз вдоль оси ОХ от оси ОУ, если 0 список " width="640"







![Семейства линий Уравнение F(x, у, а) = 0 при каждом фиксированном значении параметра а задает на плоскости XOY линию. При изменении параметра а получают множество линий, которое называется семейством линий [1].](https://fsd.multiurok.ru/html/2017/06/10/s_593c1db406cfa/img18.jpg)

















 а – х не имеет решений [1]. 1.5 При каких значениях параметра а данное уравнение имеет единственный корень 1.6 При каком значении параметра а уравнение a = | -6|x|+3| имеет а) 4 корня; б) 8 корней? Ответ: a Решение Решение Ответ: -2 Решение Ответ: а) 0; 6; б) (0; 3). " width="640"
а – х не имеет решений [1]. 1.5 При каких значениях параметра а данное уравнение имеет единственный корень 1.6 При каком значении параметра а уравнение a = | -6|x|+3| имеет а) 4 корня; б) 8 корней? Ответ: a Решение Решение Ответ: -2 Решение Ответ: а) 0; 6; б) (0; 3). " width="640"
 неравенство не имеет решений. Ответ: а задачи " width="640"
неравенство не имеет решений. Ответ: а задачи " width="640"

 a ϵ(-∞;-2] Рассмотрим два графика галочка, вершины которой имеют координаты (-а;а+2) Подсказка График Решение Ответ Ответ: (-∞;-2] задачи " width="640"
a ϵ(-∞;-2] Рассмотрим два графика галочка, вершины которой имеют координаты (-а;а+2) Подсказка График Решение Ответ Ответ: (-∞;-2] задачи " width="640"

















![y x 0 1 4 Условие задачи выполняется, если а=0, или точка пересечения данной прямой с осью Х находится в промежутке ( -3; 1]. y 2 +(x+1) 2 =2 2 , y= - a(x+4)+2 где y 0 задачи](https://fsd.multiurok.ru/html/2017/06/10/s_593c1db406cfa/img57.jpg)







![Иногда параметр удобно рассматривать как полноценную переменную, аргумент или функцию. Тогда одна из осей будет координатной, а другая называется параметрической, а координатная плоскость – координатно-параметрической. Данный способ основан на нахождении множества всех точек координатно-параметрической плоскости, значения координаты и параметра а каждой из которых удовлетворяют заданному в условиях задачи соотношению. Этот метод называется координатно-параметрическим и впервые был применен преподавателем МГУ В.П. Моденовым более тридцати лет назад [2].](https://fsd.multiurok.ru/html/2017/06/10/s_593c1db406cfa/img65.jpg)
![х 2 +a 2 =4, a=|x| 2.1 При каких значениях параметра а система имеет 2 решения? 2.2 При каких значениях параметра уравнение |2x+3|+|2x-3|= ах + 6 имеет более двух корней [4]. 2.3 Найти все значения параметра а, при каждом из которых уравнение (а+4х-х 2 -1)(а + 1-|x-2|)=0 имеет ровно три корня [1]. Ответ: Решение Ответ: 0. Решение Ответ:-1 Решение 6](https://fsd.multiurok.ru/html/2017/06/10/s_593c1db406cfa/img66.jpg)





 0. Пусть уравнение Р(х;у)=0 задает некоторые линии на плоскости. Разобьем этими линиями координатную плоскость на конечное число областей G 1, G 2, …G i , ограниченных линиями Р=0 Теорема: В каждой из областей G i, на которые линии Р(х;у)=0 делят координатную плоскость, многочлен Р(х; у) либо положителен, либо отрицателен. Таким образом, решение неравенства Р(х;у)0 - множество всех пар (х;у), при которых неравенство выполняется, образует объединение тех областей G i , в которых значение многочлена Р(х;у) положительно. Для определения знака многочлена в областях достаточно определить знак в любой точке из этой области [2]. " width="640"
0. Пусть уравнение Р(х;у)=0 задает некоторые линии на плоскости. Разобьем этими линиями координатную плоскость на конечное число областей G 1, G 2, …G i , ограниченных линиями Р=0 Теорема: В каждой из областей G i, на которые линии Р(х;у)=0 делят координатную плоскость, многочлен Р(х; у) либо положителен, либо отрицателен. Таким образом, решение неравенства Р(х;у)0 - множество всех пар (х;у), при которых неравенство выполняется, образует объединение тех областей G i , в которых значение многочлена Р(х;у) положительно. Для определения знака многочлена в областях достаточно определить знак в любой точке из этой области [2]. " width="640"
 0. Алгоритм Найти на КП-плоскости ОДЗ. Построить на КП-плоскости линии, состоящие из точек, в которых Р(х;а)=0 или не существует. Определить знаки выражения Р(х;а) в каждой из областей (для этого достаточно установить знак выражения в какой-нибудь точке области). Найти ответ. " width="640"
0. Алгоритм Найти на КП-плоскости ОДЗ. Построить на КП-плоскости линии, состоящие из точек, в которых Р(х;а)=0 или не существует. Определить знаки выражения Р(х;а) в каждой из областей (для этого достаточно установить знак выражения в какой-нибудь точке области). Найти ответ. " width="640"
![3.1 Изобразите множество точек, координаты которых удовлетворяют неравенству (х-у)(ху-1)≤0 на координатной плоскости 3.2 Изобразите множество точек, координаты которых удовлетворяют на координатной плоскости неравенству 0 [9]. 3.3 А. Л. Семенов, И. В. Ященко. Типовые тестовые задания.2013 год. Вар. 5, С5 . Найти все значения параметра а, при каждом из которых система неравенств не имеет решения. 3.4 А. Л. Семенов, И. В. Ященко. Типовые тестовые задания.2014 год. Вар. 2, С5 . Найти все значения параметра а, при каждом из которых неравенство | | имеет единственное решение на отрезке [ 1;3 ] Решение Решение Решение Решение](https://fsd.multiurok.ru/html/2017/06/10/s_593c1db406cfa/img74.jpg)








![Х = а х + - - -2 0 а + + - Ответ: (-2;0] задачи](https://fsd.multiurok.ru/html/2017/06/10/s_593c1db406cfa/img83.jpg)
![3.4 А. Л. Семенов, И. В. Ященко. Типовые тестовые задания.2014 год. Вар. 2, С5 . Найти все значения параметра а, при каждом из которых неравенство | | имеет единственное решение на отрезке [ 1;3 ] Решение: Приведем к виду: . ОДЗ: х ≠а |х 2 -2х-а| |2х-2а|; 0; (х 2 -2х-а+2х-2а)(х 2 -2х-а-2х+2а) 0; (х 2 -3а)(х 2 -4х+а) 0; (*) Решим методом областей. Решением уравнения (х 2 -3а)(х 2 -4х+а=0 является объединение двух парабол: а= х 2 и а=4х-х 2 , которые разбивают координатную плоскость на 5 областей. Расставим знаки левой части неравенства (*) в полученных областях. задачи](https://fsd.multiurok.ru/html/2017/06/10/s_593c1db406cfa/img84.jpg)
![a a ≠х а=4х- х 2 a = По графику можно опреде лить, что неравенство имеет единственное решение на отрезке[1; 3] при а=3. Ответ: 3 - + a =3. + x 0 1 + - задачи](https://fsd.multiurok.ru/html/2017/06/10/s_593c1db406cfa/img85.jpg)






















