Предмет: математика
Дата проведения: 6.12.2021г
Преподаватель: Касымова У.Ш.
Группа:1-9 « сварщики»
Тема программы: Декартовы КООРДИНАТЫ ВЕКТОРА В ПРОСТРАНСТВЕ.
Тема: Векторы в пространстве
Цели урока: Обучающая: Изучить, что такое “вектор в пространстве", как определяются координаты, вектора, если известны координаты его начала и конца, научитесь решать задачи, связанные с вектором. Обобщить свои знания о векторах в координатах также научитесь выполнять эти действия.
Развивающая: Развивать мышление, память.
Воспитывающая: Воспитать интерес к уроку.
Литература:(А.В. Погорелов «Геометрия» 10-11 класс)
Ход урока
В пространстве, как и на плоскости, вектором называется величина, которая задается своей длиной и направлением. Вектор изображается направленным отрезком, длина которого равна длине вектора. Буквально так же, как и на плоскости, определяются основные понятия для векторов в пространстве: абсолютная величина вектора, направление вектора, равенство векторов.
Но это не простое повторение, а обобщение, распространение свойств двумерной геометрии на трехмерную. Если в планиметрии для задания вектора достаточно указать две его координаты, то в стереометрии — три координаты.
Определение. Координатами вектора  , начало которого точка A(x1,y1,z1), а конец — точка В(х2, у2, z2), называются числа a1= х2- x1, a2=y2-y1, a3=z2-z1.
, начало которого точка A(x1,y1,z1), а конец — точка В(х2, у2, z2), называются числа a1= х2- x1, a2=y2-y1, a3=z2-z1.
Записывают такой вектор, указывая его координаты:  (a1 а2, а3) или
(a1 а2, а3) или  (a1 а2, а3).
(a1 а2, а3).
Например, если точки А(4; 0; 3) и B(0; 6; 4) — начало и конец направленного отрезка  , тогда
, тогда
а1 = 0 - 4 = -4, а2 = 6 - 0 = 6, а3 = 4 - 3 = 1.
Значит, направленному отрезку  соответствует вектор
соответствует вектор  (-4; 6; 1
(-4; 6; 1
Так же, как и на плоскости, равные векторы имеют соответственно равные координаты и, обратно, векторы с соответственно равными координатами равны. Это дает основание говорить о том, что любой вектор можно отложить от любой точки пространства. 
Длину вектора  (a1 а2, а3) можно выразить через его координаты. Отложим вектор
(a1 а2, а3) можно выразить через его координаты. Отложим вектор  от начала координат (рис. 68). Тогда четырехугольник OPAN — прямоугольник. Его стороны равны а1 и а2, поэтому ОАz2 = а12 + а22. В прямоугольном треугольнике ОА2 А второй катет Аz А = а3 и ОА2 = ОА2г + а32 = а12 + а22+ а32. Отсюда |
от начала координат (рис. 68). Тогда четырехугольник OPAN — прямоугольник. Его стороны равны а1 и а2, поэтому ОАz2 = а12 + а22. В прямоугольном треугольнике ОА2 А второй катет Аz А = а3 и ОА2 = ОА2г + а32 = а12 + а22+ а32. Отсюда | | =
| = 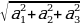
Длина любого ненулевого вектора — число положительное. Длина нулевого вектора равна нулю.
Вспомним, что два вектора, лежащих на одной прямой или параллельных прямых, называют коллинеарными. Коллинеарные векторы бывают сонаправлены (а 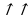 b) или противоположно направлены (а
b) или противоположно направлены (а  b). Если векторы ON и ОМ коллинеарны, то точки О, N, М лежат на одной прямой. Нулевые векторы не имеют направлений и считаются коллинеарными к любому вектору.
b). Если векторы ON и ОМ коллинеарны, то точки О, N, М лежат на одной прямой. Нулевые векторы не имеют направлений и считаются коллинеарными к любому вектору.
4. Закрепление
1.Точки С(4;1;-1) и D(0;5;5) делят отрезок АВ на три равные части. Найдите длину отрезка АВ.
а) 6 в)11 . с)9 d) 8

uma.kasymova@mail.ru
Указать дату, Ф.И.О и группу
Предмет: математика
Дата проведения:7.12.2021
Преподаватель: Касымова У.Ш.
Группа:1-8 « сварщики»
Тема программы: Декартовы КООРДИНАТЫ ВЕКТОРА В ПРОСТРАНСТВЕ.
Тема: Действия над векторами в координатах.
Цель: Обучающая: ввести понятие вектора в пространстве, равенства векторов. Рассмотреть правила действия над векторами, правило сложения.
Развивающая: Развивать умение быстро ориентироваться в пространстве
Воспитывающая: Воспитать доброжелательность по отношению к окружающим, внимательность, дисциплинированность.
Литература: (А.В. Погорелов «Геометрия» 10-11 класс)
Ход урока.
Действия над векторами в пространстве осуществляются аналогично тому, как они определялись для векторов на плоскости.
Определение. Суммой векторов a (a1 а2, а3) и b(b1 b2, b3) называется вектор а + b с координатами (а1 + b1; а2 + b2 ; а3 + b3)
Для любых векторов а , b и с справедливы равенства:
а+b=b+а — переместительный закон сложения;
а + (b + с) = (а+ b) + с — сочетательный закон сложения.
Чтобы доказать эти свойства, достаточно сравнить соответствующие
координаты левой и правой частей каждого векторного равенства.
Для любых трех точек А, В, С в пространстве имеет место векторное равенство  +
+ 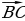 =
= 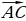 .
.
Действительно, для любых трех точек A(a1 а2, а3), B(b1 b2, b3), C(c1, с2, с3)  (b1 – а1; b2 - а2; b3 - а3) и
(b1 – а1; b2 - а2; b3 - а3) и 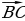 (с1 - bг; с2 - b2, с3 - b3).
(с1 - bг; с2 - b2, с3 - b3).
Отсюда  +
+ 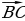 =
= 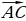 (с1 – а1; с2 - а2; с3 - а3).
(с1 – а1; с2 - а2; с3 - а3).
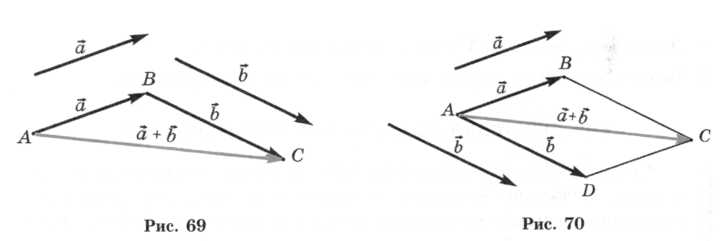
Геометрически сумму двух векторов пространства можно находить, пользуясь правилам треугольника (рис. 69).
Также применяется и правило параллелограмма. Оно часто используется в физике.
Если ABCD — параллелограмм (рис. 70), то  +
+  =
= 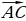 .
.
Чтобы найти сумму нескольких векторов, используем правило многоугольника. Например, если в пространстве даны точки А, В, С, D, Е, F, то всегда
АВ + ВС +CD + DE + EF = AF.
Определение. Два вектора, сумма которых равна нулевому вектору, называются противоположными.
Из определения следует, что у противоположных векторов соответствующие координаты имеют противоположные знаки.
Определение. Разностью векторов а и b называется такой вектор с , который в сумме с вектором b дает вектор а .
Если а (а1; а2; а3) и b( b1; b2; b3), то 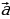 -
-  =
=  (а1 –b1; а2 - b2; а3 – b3).
(а1 –b1; а2 - b2; а3 – b3).
Определение. Произведением вектора  (a1; а2; a3) на число k называется вектор k
(a1; а2; a3) на число k называется вектор k 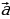 = (k а1; k а2; k а3).
= (k а1; k а2; k а3).
Из определения вытекают следующие свойства: 1)k( +
+ 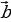 ) =k
) =k + k
+ k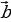 ,
,
2)(т + n) • 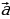 =т
=т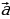 +п
+п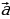 и равенство | k •
и равенство | k • 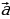 | = | k |•|
| = | k |•| 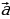 | (здесь k, т, п — числа). Скалярным произведением (а1;а2;а3) и (в1;в2;в3) наз. число а1в1+а2в2+а3в3
| (здесь k, т, п — числа). Скалярным произведением (а1;а2;а3) и (в1;в2;в3) наз. число а1в1+а2в2+а3в3
Ненулевые векторы а и b коллинеарные тогда и только тогда, когда найдется такое число х, что выполняется равенство 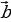 = х
= х 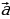 . При этом число х единственно.
. При этом число х единственно.
4. Закрепление 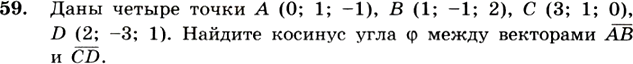

6.Подведение итогов урока. Указать дату, Ф.И.О и группу
uma.kasymova@mail.ru
Предмет: математика
Дата проведения:8.12.2021г
Группа: 1-8 « сварщики»
Преподаватель: Касымова У.Ш
Тема программы: Декартовы координаты и векторы
Тема урока: решение задач
Цель: Обучающая: закрепить понятие о векторах , решать задачи по теме урока
Развивающая: развивать мышление, сообразительность, навыки.
Воспитывающая: воспитать работу в коллективе
Литература: Погорелов 10-11кл.
Ход урока:
2. Повторение
Как найти угол между скрещивающимися прямыми?
Как найти угол между плоскостями?
Как найти сумму векторов?
Чтобы найти координаты вектора  , если заданы координаты его начала и конца, необходимо от координат конца отнять соответствующие координаты начала. В случае если точки заданы на плоскости и имеют соответственно координаты
, если заданы координаты его начала и конца, необходимо от координат конца отнять соответствующие координаты начала. В случае если точки заданы на плоскости и имеют соответственно координаты  и
и 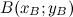 , то координаты вектора
, то координаты вектора  вычисляются по формуле:
вычисляются по формуле: 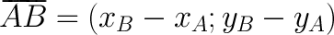
Если точки заданы в пространстве и имеют координаты  и
и 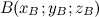 соответственно, то координаты вектора
соответственно, то координаты вектора  вычисляются по следующей формуле:
вычисляются по следующей формуле:
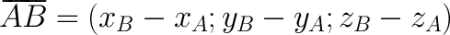
Примеры нахождения координат вектора Задание№1. Даны точки 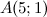 и
и 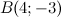 . Найти координаты векторов
. Найти координаты векторов  и
и 
Решение. Точки заданны на плоскости, поэтому координаты вектора  вычислим по формуле:
вычислим по формуле:
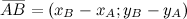
Подставляя координаты заданных точек, получим:
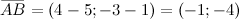
Для нахождения вектора  исходная формула примет вид:
исходная формула примет вид:
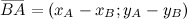
то есть

Ответ. 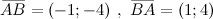 Пример
Пример
Задание№2. Даны точки 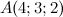 ,
,  и
и  . Найти координаты вектора
. Найти координаты вектора  ,
,  .
.
Решение. Точки заданны в пространстве, поэтому для нахождения координат искомых векторов будем пользоваться формулой
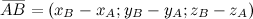
Подставляя заданные координаты, получим:
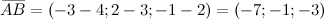
Для вектора  имеем:
имеем:

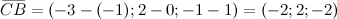
Ответ. 
Задача № 3 Найти координаты вектора АВ, если А(-3;3;12)и В(5;-2;-4)
Решение: Чтобы найти сумму векторов 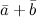 , которые заданны координатами
, которые заданны координатами 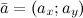 и
и  , необходимо сложить соответствующие координаты этих векторов, то есть
, необходимо сложить соответствующие координаты этих векторов, то есть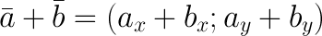
В случае если векторы заданы в пространстве, то есть 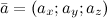 и
и 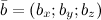 , то их сумма равна
, то их сумма равна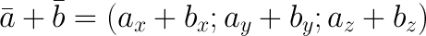
Примеры нахождения суммы векторов мер
Задание№4. Найти сумму векторов 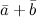 ,
, 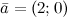 и
и 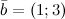
Решение. Для нахождения суммы векторов, сложим их соответствующие координаты
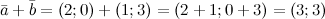
Ответ. 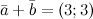
Задание№5. Найти суммы векторов 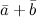 ,
, 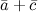 ,
, 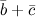 и
и 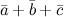 , если
, если 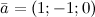 ,
,  и
и 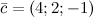
Решение. Для нахождения искомой суммы векторов сложим их соответствующие координаты:

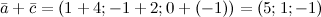
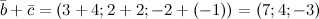
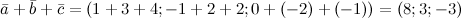
Ответ. 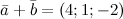 ,
, 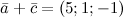 ,
, 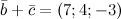 ,
, 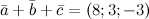
Задача № 6найти сумму векторов а(-3; -5;-4) и b(-6; -4; -10)
Задача № 7 Найдите сумму векторов: а) АВ и АС б) PR и PS в) AB,BD,CD и DA
Решение: А) АВ + АС=ВС; б) PR + PS=RS; в) AB+BD+CD+DA=AD+CD=AC+DA=CD
4 этап: домашнее задание 1) Найти координаты вектора АВ, если А(-3;7;1)и В(-1;2;5
2)найти сумму векторов а(3; --2;-4) и b(-4; -2; 10) 5 этап:
итог урока Указать дату, Ф.И.О и группу uma.kasymova@mail.ru
Дата проведения:10.12.2021г
Преподаватель: Касымова У.Ш
Группа:1-8 «сварщики»
Тема урока: «Двугранный угол» Трехгранные и многогранные углы.
Цели урока:
Образовательные: Знакомство с понятием двугранного угла и его линейного угла, обучение построению линейного угла данного двугранного угла путем поисковой, исследовательской деятельности
Развивающие: Развитие навыков построения перпендикуляра к плоскости, формирование конструктивного навыка нахождения угла между плоскостями, развитие памяти, логического мышления, любознательности.
Воспитательные: Воспитание усидчивости, внимания, взаимоуважения, целеустремленности, самостоятельности учащихся
Ход урока:
1. Организационный момент.
Включает в себя приветствие учителем класса, подготовку помещения к уроку, проверку отсутствующих.
2. Проверка домашней работы.
Постановка цели урока.
Сегодня мы с вами должны подняться ещё на одну ступеньку вверх, «преодолевая» задачи, которые будут рассматриваться на уроке. Мы познакомимся с новым понятием «Двугранный угол» .
Актуализация опорных знаний.
Ответ: Наименьший из четырех углов, получающихся при пересечении двух прямых.
Ответ: Угол между прямой и ее проекцией.
Ответ: Сама точка, если она лежит в плоскости проекции, основание перпендикуляра, проведенного из точки к плоскости, для точки не принадлежащей плоскости проекций.
Что является проекцией прямой на плоскость, не перпендикулярную данной прямой?
Ответ: Проекцией наклонной является прямая.
3 . Изучение нового материала.
Запишем определение двугранного угла:
Определение. Двугранным углом, называется фигура, образованная прямой и двумя полуплоскостями с общей границей , не принадлежащими одной плоскости.
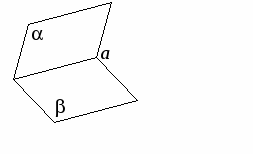
Полуплоскости, образующие двугранный угол называются его гранями. У двугранного угла две грани, отсюда и название – двугранный угол. Прямая – общая граница полуплоскостей – называется ребром двугранного угла.
Мы знаем, что углы на плоскости ( обычные углы ) измеряются в градусах. А как измеряются двугранные углы? Это делается следующим образом. Отметим на ребре двугранного угла какую – нибудь точку и в каждой грани из этой точки проведем луч перпендикулярно к ребру. Образованный этими лучами угол называется линейным углом двугранного угла.

Все линейные углы двугранного угла равны друг другу.
Два двугранных угла считаются равными, если они при вложении могут совместиться; в противном случае тот из углов, который составит часть другого угла, считается меньшим.
Градусной мерой двугранного угла называется градусная мера его линейного угла.
Можно рассматривать сумму, разность, произведение и частное двугранных углов в том же смысле, как и для углов планиметрии. Подобно этим углам, двугранные углы могут быть смежные и вертикальные. Если два смежных двугранных угла равны между собой, то каждый из них называется прямым двугранным углом.
4.Закрепление
Задача 2. - ромб, см, прямая перпендикулярна плоскости , см. Двугранный угол с ребром равен 45о. Найти площадь ромба.

Решение: Опустим перпендикуляр на , - точка пересечения диагоналей. Двугранный угол равен линейному углу , тогда см, отсюда следует, что см и см. Тогда (см2)
Указать дату, Ф.И.О и группу uma.kasymova@mail.ru






 , начало которого точка A(x1,y1,z1), а конец — точка В(х2, у2, z2), называются числа a1= х2- x1, a2=y2-y1, a3=z2-z1.
, начало которого точка A(x1,y1,z1), а конец — точка В(х2, у2, z2), называются числа a1= х2- x1, a2=y2-y1, a3=z2-z1. (a1 а2, а3).
(a1 а2, а3). (-4; 6; 1
(-4; 6; 1
 (a1 а2, а3) можно выразить через его координаты. Отложим вектор a
(a1 а2, а3) можно выразить через его координаты. Отложим вектор a
 b) или противоположно направлены (а ↑↓
b) или противоположно направлены (а ↑↓ b). Если векторы ON и ОМ коллинеарны, то точки О, N, М лежат на одной прямой. Нулевые векторы не имеют направлений и считаются коллинеарными к любому вектору.
b). Если векторы ON и ОМ коллинеарны, то точки О, N, М лежат на одной прямой. Нулевые векторы не имеют направлений и считаются коллинеарными к любому вектору. , начало которого точка A(x1,y1,z1), а конец — точка В(х2, у2, z2), называются числа a1= х2- x1, a2=y2-y1, a3=z2-z1.
, начало которого точка A(x1,y1,z1), а конец — точка В(х2, у2, z2), называются числа a1= х2- x1, a2=y2-y1, a3=z2-z1.  (a1 а2, а3).
(a1 а2, а3).
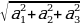
 b) или противоположно направлены (а
b) или противоположно направлены (а  b). Если векторы ON и ОМ коллинеарны, то точки О, N, М лежат на одной прямой. Нулевые векторы не имеют направлений и считаются коллинеарными к любому вектору.
b). Если векторы ON и ОМ коллинеарны, то точки О, N, М лежат на одной прямой. Нулевые векторы не имеют направлений и считаются коллинеарными к любому вектору.
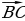 =
= 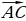 .
. =
= 
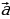 -
- 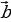 =
= 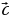 (а1 –b1; а2 - b2; а3 – b3).
(а1 –b1; а2 - b2; а3 – b3).




















