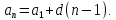ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
Числовой последовательностью называется бесконечное множество чисел 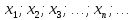 следующих одно за другим в определённом порядке и построенных по определённому закону, с помощью которого
следующих одно за другим в определённом порядке и построенных по определённому закону, с помощью которого 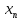 задаётся как функция целочисленного аргумента n, то есть
задаётся как функция целочисленного аргумента n, то есть 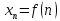 .
.
Существует несколько способов задания числовой последовательности.
Аналитический. Этот способ состоит в том, что задана формула п-го члена.
Например, 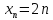 - последовательность чётных положительных чисел;
- последовательность чётных положительных чисел;
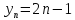 – последовательность нечётных положительных чисел;
– последовательность нечётных положительных чисел;
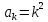 – последовательность квадратов целых чисел.
– последовательность квадратов целых чисел.
Описательный (или словесный). Этот способ задания последовательности состоит в том, что объясняется, из каких элементов строится последовательность.
Например, «все члены последовательности равны 1». Это означает, что речь идёт о стационарной последовательности 1; 1; 1; 1; …
«Последовательность состоит из всех простых чисел в порядке возрастания», т.е. задана последовательности 2; 3; 5; 7; 11; 13; …
Рекуррентный. Этот способ задания последовательности состоит в том, что указывается правило, позволяющее вычислить n-й член последовательности, если известны её предыдущие члены.
Например, 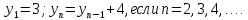
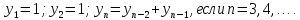
Графический. В этом случае числовая последовательность задаётся графиком, который представляет собой изолированные точки. Абсциссы этих точек — натуральные числа: 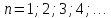 . Ординаты — значения членов последовательности:
. Ординаты — значения членов последовательности: 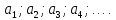
Например, каждая точка в этой координатной плоскости имеет координаты 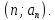 Выпишем координаты отмеченных точек по возрастанию абсциссы n.
Выпишем координаты отмеченных точек по возрастанию абсциссы n.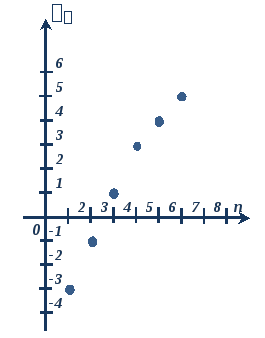
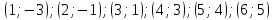
Значит, 
Последовательность  называют возрастающей, если каждый её член (кроме первого) больше предыдущего:
называют возрастающей, если каждый её член (кроме первого) больше предыдущего: 
Последовательность 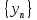 называют убывающей, если каждый её член (кроме первого) меньше предыдущего:
называют убывающей, если каждый её член (кроме первого) меньше предыдущего: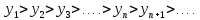
Возрастающие и убывающие последовательности объединяют общим термином – монотонные последовательности.
Например, 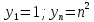 – возрастающая последовательность;
– возрастающая последовательность;
 – убывающая последовательность;
– убывающая последовательность;
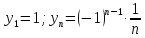 – эта последовательность не является ни возрастающей, ни убывающей.
– эта последовательность не является ни возрастающей, ни убывающей.
АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
Арифметическая прогрессия — это последовательность, каждый член которой (начиная со второго) равен сумме предыдущего члена и некоторого фиксированного числа:
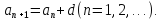
Фиксированное число d называется разностью арифметической прогрессии.
Например, последовательность 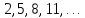 является арифметической прогрессией с первым членом 2 и разностью 3.
является арифметической прогрессией с первым членом 2 и разностью 3.
,
Формула для 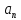 имеет вид:
имеет вид:
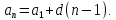
Формула суммы  первых n членов арифметической прогрессии имеет вид:
первых n членов арифметической прогрессии имеет вид:
 .
.
или
.
Свойство арифметической прогрессии. Если числа  образуют арифметическую прогрессию, то
образуют арифметическую прогрессию, то 
ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
Геометрическая прогрессия — это последовательность, каждый член которой (начиная со второго) равен произведению предыдущего члена и некоторого фиксированного числа:

Фиксированное число q называется знаменателем геометрической прогрессии.
Например, последовательность  является геометрической прогрессией с первым членом 2 и знаменателем 3.
является геометрической прогрессией с первым членом 2 и знаменателем 3.
Если знаменатель  то такая последовательность называется бесконечной убывающей геометрической прогрессией.
то такая последовательность называется бесконечной убывающей геометрической прогрессией.
Формула n-го члена геометрической прогрессии имеет вид:

Формула суммы  первых n членов геометрической прогрессии:
первых n членов геометрической прогрессии:

Сумма бесконечной убывающей геометрической прогрессии вычисляется по формуле:

Свойство геометрической прогрессии. Пусть числа  образуют геометрическую прогрессию. Тогда
образуют геометрическую прогрессию. Тогда  .
.
В геометрической прогрессии  известно, что
известно, что  . Найти пятый член этой прогрессии.
. Найти пятый член этой прогрессии.
Решение. 
Ответ: 
Геометрическая прогрессия  задана формулой п-го члена
задана формулой п-го члена  . Укажите четвёртый член этой прогрессии.
. Укажите четвёртый член этой прогрессии.
Решение.
Ответ: 
Дана геометрическая прогрессия  , знаменатель которой равен 2, а
, знаменатель которой равен 2, а  . Найдите сумму первых шести её членов.
. Найдите сумму первых шести её членов.
Решение.
Ответ: 
В геометрической прогрессии сумма первого и второго членов равна 75, а сумма второго и третьего членов равна 150. Найдите первые три члена этой прогрессии.
В ответе запишите первый, второй и третий члены прогрессии без пробелов.
Решение.
Решим систему:


Ответ: 
Геометрическая прогрессия задана условием  . Найдите сумму первых её 4 членов.
. Найдите сумму первых её 4 членов.
Решение.
Ответ: 
Выписаны первые несколько членов геометрической прогрессии:  Найдите её четвёртый член.
Найдите её четвёртый член.
Решение.
Ответ: 
Выписано несколько последовательных членов геометрической прогрессии:  Найдите член прогрессии, обозначенный буквой x.
Найдите член прогрессии, обозначенный буквой x.
Решение. Воспользуемся свойством геометрической прогрессии: 
. Так как члены прогрессии положительны, то 
Ответ: 
Выписаны первые несколько членов геометрической прогрессии:  Найдите сумму первых пяти её членов.
Найдите сумму первых пяти её членов.
Решение.
Ответ: 
Дана геометрическая прогрессия  , для которой
, для которой  Найдите знаменатель прогрессии.
Найдите знаменатель прогрессии.
Решение.
Ответ: 
Геометрическая прогрессия задана условием  . Найдите сумму первых 5 её членов.
. Найдите сумму первых 5 её членов.
Решение.
Ответ: 
Дана арифметическая прогрессия:  . Найдите сумму первых 10 её членов.
. Найдите сумму первых 10 её членов.
Решение. 
Ответ: 
Дана арифметическая прогрессия  :
:  . Найдите
. Найдите  .
.
Решение.
Ответ: 
Выписаны первые несколько членов арифметической прогрессии:  Какое из следующих чисел есть среди членов этой прогрессии?
Какое из следующих чисел есть среди членов этой прогрессии?
1) 83 2) 95 3) 100 4) 102
Решение. . Значит, эта прогрессия состоит из чисел, кратных 3. Из перечисленных чисел только 102 делится на 3, поэтому это число является членом данной арифметической прогрессии.
Ответ: 
Арифметические прогрессии  заданы формулами n-го члена:
заданы формулами n-го члена:  ,
, ,
,  . Укажите те из них, у которых разность равна 4.
. Укажите те из них, у которых разность равна 4.
1)  и
и  2)
2)  и
и  3)
3)  и
и  4)
4) 
Решение.
Ответ: 
В первом ряду кинозала 30 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в ряду с номером n?
1)  2)
2)  3)
3)  4)
4) 
Решение.
Ответ: 
Дана арифметическая прогрессия:  Найдите первый отрицательный член этой прогрессии.
Найдите первый отрицательный член этой прогрессии.
1)  2)
2)  3)
3)  4)
4) 
Решение.
Т.к.  , то . Т.к.
, то . Т.к.  – порядковый номер, то
– порядковый номер, то  . Значит,
. Значит, 
Ответ: 
Арифметическая прогрессия задана условиями:  , . Какое из данных чисел является членом этой прогрессии?
, . Какое из данных чисел является членом этой прогрессии?
1)  2)
2)  3)
3)  4)
4) 
Решение. 
. Значит, членами данной прогрессии являются числа, кратные 6. Из всех приведённых чисел только число 48 кратно 6.
Ответ: 
Найдите сумму всех отрицательных членов арифметической прогрессии: 
Решение. . Найдём количество отрицательных членов: . Т.к.  , то . Значит,
, то . Значит,  .
.
Ответ: 
Какое наибольшее число последовательных натуральных чисел, начиная с 1, можно сложить, чтобы получившаяся сумма была меньше 528?
Решение. 
. Т.к.  , то
, то
. Т.к.  – порядковый номер, то наибольшее число из этого промежутка -
– порядковый номер, то наибольшее число из этого промежутка - 
Ответ: 
Записаны первые три члена арифметической прогрессии:  Какое число стоит в этой арифметической прогрессии на 91-м месте?
Какое число стоит в этой арифметической прогрессии на 91-м месте?
Решение.
Ответ: 
Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 8 квадратов больше, чем в предыдущей. Сколько квадратов в 16-й строке?
Решение. 

Ответ: 
Выписано несколько последовательных членов арифметической прогрессии:  Найдите член прогрессии, обозначенный буквой x.
Найдите член прогрессии, обозначенный буквой x.
Решение. Воспользуемся свойством арифметической прогрессии:
Ответ: 
Дана арифметическая прогрессия  для которой
для которой  Найдите разность прогрессии.
Найдите разность прогрессии.
Решение.
Ответ: 
Последовательность задана формулой  . Какое из указанных чисел является членом этой последовательности?
. Какое из указанных чисел является членом этой последовательности?
1)  2)
2)  3)
3)  4)
4) 
Решение. 



Т.к.  – порядковый номер, то он должен быть положительным целым числом. Из всех рассмотренных вариантов этим условиям удовлетворяет только
– порядковый номер, то он должен быть положительным целым числом. Из всех рассмотренных вариантов этим условиям удовлетворяет только  . Значит, число 3 является членом данной последовательности.
. Значит, число 3 является членом данной последовательности.
Ответ: 
Какое из указанных чисел не является членом последовательности 
1)  2)
2)  3)
3)  4)
4) 
Решение. Рассмотрим знаменатели. Т.к. в первом случае знаменатель чётный, то при возведении отрицательного числа в чётную степень получается положительное число, т.е.  . Аналогичные рассуждения для второго и третьего случаев. Для четвёртого случая: знаменатель нечётное число, значит, дробь должна быть отрицательной, а у нас она положительная. Это означает, что
. Аналогичные рассуждения для второго и третьего случаев. Для четвёртого случая: знаменатель нечётное число, значит, дробь должна быть отрицательной, а у нас она положительная. Это означает, что  не является членом данной последовательности.
не является членом данной последовательности.
Ответ: 
Последовательность задана формулой  . Сколько членов в этой последовательности больше 1?
. Сколько членов в этой последовательности больше 1?
1)  2)
2)  3)
3)  4)
4) 
Решение. Т.к.  , то . Т.к.
, то . Т.к.  – порядковый номер, то
– порядковый номер, то  . В этом промежутке ровно 9 целых значений, значит, в последовательности 9 членов, больших 1.
. В этом промежутке ровно 9 целых значений, значит, в последовательности 9 членов, больших 1.
Ответ: 
Какая из следующих последовательностей является арифметической прогрессией?
1) Последовательность натуральных степеней числа 2.
2) Последовательность натуральных чисел, кратных 5.
3) Последовательность кубов натуральных чисел.
4) Последовательность всех правильных дробей, числитель которых на 1 меньше знаменателя.
Решение. 1)  . Данная последовательность является геометрической прогрессией, т.к. каждое последующее число в 2 раза больше предыдущего;
. Данная последовательность является геометрической прогрессией, т.к. каждое последующее число в 2 раза больше предыдущего;
2)  . В этой последовательности каждое следующее число на 5 больше предыдущего, значит, это арифметическая прогрессия;
. В этой последовательности каждое следующее число на 5 больше предыдущего, значит, это арифметическая прогрессия;
3)  . Эта последовательность не является ни арифметической прогрессией, ни геометрической, т.к. не соблюдается одно и то же изменение последующего числа по сравнению с предыдущим;
. Эта последовательность не является ни арифметической прогрессией, ни геометрической, т.к. не соблюдается одно и то же изменение последующего числа по сравнению с предыдущим;
4)  . Эта последовательность не является ни арифметической прогрессией, ни геометрической, т.к. не соблюдается одно и то же изменение последующего числа по сравнению с предыдущим.
. Эта последовательность не является ни арифметической прогрессией, ни геометрической, т.к. не соблюдается одно и то же изменение последующего числа по сравнению с предыдущим.
Ответ: 
4







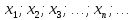 следующих одно за другим в определённом порядке и построенных по определённому закону, с помощью которого
следующих одно за другим в определённом порядке и построенных по определённому закону, с помощью которого 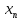 задаётся как функция целочисленного аргумента n, то есть
задаётся как функция целочисленного аргумента n, то есть 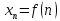 .
.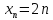 - последовательность чётных положительных чисел;
- последовательность чётных положительных чисел;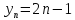 – последовательность нечётных положительных чисел;
– последовательность нечётных положительных чисел;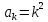 – последовательность квадратов целых чисел.
– последовательность квадратов целых чисел.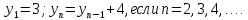
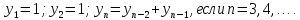
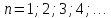 . Ординаты — значения членов последовательности:
. Ординаты — значения членов последовательности: 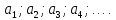
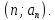 Выпишем координаты отмеченных точек по возрастанию абсциссы n.
Выпишем координаты отмеченных точек по возрастанию абсциссы n.
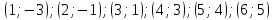

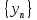 называют возрастающей, если каждый её член (кроме первого) больше предыдущего:
называют возрастающей, если каждый её член (кроме первого) больше предыдущего: 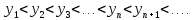
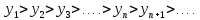
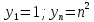 – возрастающая последовательность;
– возрастающая последовательность; – убывающая последовательность;
– убывающая последовательность;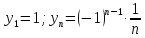 – эта последовательность не является ни возрастающей, ни убывающей.
– эта последовательность не является ни возрастающей, ни убывающей.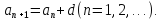
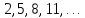 является арифметической прогрессией с первым членом 2 и разностью 3.
является арифметической прогрессией с первым членом 2 и разностью 3. 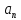 имеет вид:
имеет вид: