Зачет по геометрии 9 класс

Геометрия , Атанасян Л. С. Подготовила: Биктанова Рита Альфитовна, 9 кл.

Раздел: в помощь ученику и учителю., г. Дюртюли,2018 год

Пояснительная записка

Ответы на вопросы к смотру знаний по геометрии для учеников 9-х классов. Это хорошая помощь при подготовке учащихся ежегодному смотру знаний по геометрии, проводящемуся среди параллели 9-х классовнашей школы в ноябре месяце. Работа содержит чертежи и краткие ответы к каждому вопросу из 78 по курсу планиметрии 7-8 кл. по учебнику Атанасяна Л.С.

Ход смотра знаний: каждый ученик, вытягивая произвольно 10 вопросов из 78, отвечает индивидуально учителю математики на вопросы. Критерии оценивания: «5»-10-9 вопрсов верно; «4»-8-7 вопрсов верно;»3»- 6-5 вопросов верно.

Вопросы к смотру знаний по геометрии

1. Сформулируйте определение перпендикулярных прямых. Сформулируйте определение и свойства смежных и вертикальных углов

2. Сформулируйте определение равнобедренного треугольника. Сформулируйте признак равнобедренного треугольника

3. Сформулируйте свойство углов при основании равнобедренного треугольника

4. Сформулируйте определение биссектрисы треугольника. Сформулируйте свойство биссектрисы равнобедренного треугольника

5. Сформулируйте определение медианы треугольника. Сформулируйте свойство медианы равнобедренного треугольника

6. Сформулируйте определение высоты треугольника. Сформулируйте свойство высоты равнобедренного треугольника

7. Сформулируйте неравенство треугольника

8. Сформулируйте определение равных треугольников. Сформулируйте признаки равенства треугольников

9. Сформулируйте определение параллельных прямых. Сформулируйте аксиому параллельных прямых. Сформулируйте признаки параллельных прямых

10. Сформулируйте теорему о сумме углов треугольника

11. Сформулируйте определение внешнего угла треугольника. Сформулируйте теорему о свойстве внешнего угла треугольника

12. Сформулируйте определение прямоугольного треугольника. Сформулируйте свойство прямоугольного треугольника

13. Сформулируйте признаки равенства прямоугольных треугольников

14. Сформулируйте теорему о зависимости между сторонами и углами треугольника

15. Сформулируйте свойство углов, образованных при пересечении параллельных прямых секущей

16. Определение четырёхугольника и его элементов. Диагональ четырёхугольника. Определение выпуклого четырёхугольника. Сумма углов выпуклого четырёхугольника

17. Определение параллелограмма. Свойства параллелограмма

18. Признаки параллелограмма

19. Определение трапеции. Виды трапеции. Свойства равнобедренной трапеции

20. Определение прямоугольника. Свойства прямоугольника. Признаки прямоугольника

21. Определение ромба. Свойства ромба

22. Определение квадрата. Свойства квадрата

23. Понятие площади многоугольника. Единица измерения площадей. Свойства площадей. Площадь квадрата

24. Определение высоты параллелограмма. Площадь параллелограмма

25. Определение высоты трапеции. Площадь трапеции

26. Площадь ромба (через диагонали). Площадь прямоугольника

27. Теорема Пифагора и обратная ей

28. Площадь прямоугольного треугольника. Теорема об отношениях площадей треугольников: с равными высотами; имеющих по равному углу

29. Определение подобных треугольников. Теоремы об отношениях периметров и площадей подобных треугольников

30. Первый признак подобия треугольников. Определение синуса острого угла прямоугольного треугольника

31. Второй признак подобия треугольников. Определение косинуса острого угла прямоугольного треугольника

32. Третий признак подобия треугольников. Определение тангенса острого угла прямоугольного треугольника

33. Определение средней линии треугольника. Свойство средней линии

34. Свойство высоты прямоугольного треугольника, приведённой из вершины прямого угла. Свойство катета прямоугольного треугольника

35. Основное тригонометрическое тождество. Значение синуса, косинуса и тангенса для углов 30^о, 45^о и 60^о

36.Каково взаимное расположение прямой и окружности в зависимости от соотношения между радиусом окружности и расстоянием от её центра до прямой?

37.Какая прямая называется секущей по отношению к окружности?

38. Какая прямая называется касательной к окружности? Какая точка называется точкой касания прямой и окружности?

39. Сформулируйте теорему о свойстве касательной к окружности.

40. Сформулируйте теорему об отрезках касательных к окружности, проведённых из одной точки.

41. Сформулируйте признак касательной (теорему, обратную теореме о свойстве касательной).

42. Какой угол называется центральным углом окружности? В каких случаях градусная мера центрального угла считается равной a, а в каких 360° - a?

43. Объясните, что такое дуга окружности? Как она обозначается? Чему равна градусная мера дуги? В каких случаях градусная мера дуги считается равной a, а в каких 360° - a?

44.Объясните, какая дуга называется полуокружностью.

45. Какой угол называется вписанным? В каком случае говорят, что вписанный угол опирается на дугу?

46. Сформулируйте и докажите теорему о вписанном угле.

47. Сформулируйте и докажите теорему о вписанных углах, опирающихся на одну и ту же дугу.

48. Сформулируйте и докажите теорему о вписанных углах, опирающихся на полуокружность.

49. Что такое хорда окружности? Какая хорда называется диаметром?

50. Сформулируйте и докажите теорему об отрезках пересекающихся хорд.

51. Чему равен угол между хордой окружности и касательной к окружности, проведённой через конец хорды?

52. Каким замечательным свойством обладают медианы, высоты и биссектрисы треугольника?

53. Какая окружность называется вписанной в треугольник? Какой треугольник называется описанным около окружности?

54. Какая окружность называется вписанной в многоугольник? Какой многоугольник называется описанным около окружности?

55. Сформулируйте теорему об окружности, вписанной в треугольник.

56. Сколько окружностей можно вписать в треугольник?

57. Какая точка является центром окружности, вписанной в треугольник?

58. Как построить окружность, вписанную в треугольник? Можно ли вписать окружность в четырёхугольник?

59. В какой четырёхугольник можно вписать окружность?

60. Можно ли вписать окружность в ромб? квадрат? параллелограмм? прямоугольник? трапецию?

61. Каким свойством обладают стороны четырёхугольника, описанного около окружности?

62. Какая окружность называется описанной около треугольника? Какой треугольник называется вписанным в окружность?

63. Какая окружность называется описанной около многоугольника? Какой многоугольник называется вписанным в окружность?

64. Сформулируйте теорему об окружности, описанной около треугольника.

65. Сколько окружностей можно описать около данного треугольника?

66. Какая точка является центром окружности, описанной около треугольника?

67. Где находится центр окружности, описанной около остроугольного треугольника?

68. Как построить окружность, описанную около остроугольного треугольника?

69. Где находится центр окружности, описанной около прямоугольного треугольника?

70. Как построить окружность, описанную около прямоугольного треугольника?

71. Где находится центр окружности, описанной около тупоугольного треугольника?

72. Как построить окружность, описанную около тупоугольного треугольника?

73. Можно ли описать окружность около четырёхугольника?

74. В каком случае около четырёхугольника можно описать окружность?

75. Можно ли описать окружность около ромба? квадрата? параллелограмма? прямоугольника? трапеции?

76. Каким свойством обладают углы четырёхугольника, вписанного в окружность?

77.В какой четырёхугольник всегда можно вписать окружность и можно описать около него окружность?

78. Какие точки называют замечательными точками треугольника?

Ответы на вопросы к смотру знаний по геометрии

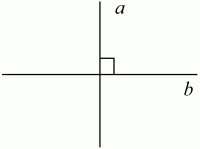
1. Сформулируйте определение перпендикулярных прямых. Сформулируйте определение и свойства смежных и вертикальных углов.

Перпендикулярные прямые – это две пересекающиеся прямые, образующие четыре прямых угла

Смежный угол – два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой

Вертикальный угол – два угла, где стороны одного угла являются продолжениями сторон другого

Свойство смежных углов – сумма смежных углов равна 180^о

Свойство вертикальных углов – вертикальные углы равны

1. Сформулируйте определение равнобедренного треугольника. Сформулируйте признак равнобедренного треугольника.

Равнобедренный треугольник – треугольник, у которого две его стороны равны

Признак равнобедренного треугольника – если в треугольнике углы при основании равны, то он равнобедренный

1. Сформулируйте свойство углов при основании равнобедренного треугольника.

Свойство углов при основании равнобедренного треугольника – в равнобедренном треугольнике углы при основании равны

1. Сформулируйте определение биссектрисы треугольника. Сформулируйте свойство биссектрисы равнобедренного треугольника.

Биссектриса треугольника – отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны

Свойство биссектрисы равнобедренного треугольника – в равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой

1. Сформулируйте определение медианы треугольника. Сформулируйте свойство медианы равнобедренного треугольника.

Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противоположной стороны

Свойство медианы равнобедренного треугольника – медиана равнобедренного треугольника, проведённая к основанию, является высотой и биссектрисой

1. Сформулируйте определение высоты треугольника. Сформулируйте свойство высоты равнобедренного треугольника.

Высота треугольника – перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону

Свойство высоты равнобедренного треугольника – высота равнобедренного треугольника, проведённая к основанию, является медианой и биссектрисой

1. Сформулируйте неравенство треугольника.

Неравенство треугольника – каждая сторона треугольника меньше суммы двух других сторон

1. Сформулируйте определение равных треугольников. Сформулируйте признаки равенства треугольников.

Равные треугольники – элементы (т.е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника

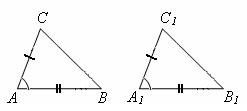
Первый признак равенства треугольников – если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углы между ними другого треугольника, то такие треугольники равны

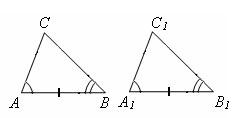
Второй признак равенства треугольников – если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны

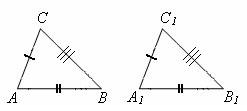
Третий признак равенства треугольников – если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны

1. Сформулируйте определение параллельных прямых. Сформулируйте аксиому параллельных прямых. Сформулируйте признаки параллельных прямых.

Параллельные прямые – две прямые на плоскости, которые не пересекаются

Аксиома параллельных прямы –через точку, не лежащую на данной прямой, проходит только одно прямая, параллельная данной

Первый признак параллельных прямых – если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны

Второй признак параллельных прямых – если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны

Третий признак параллельных прямых - если при пересечении двух прямых секущей сумма односторонних углов равно 180^о, то прямые параллельны

1. Сформулируйте теорему о сумме углов треугольника.

Теорема о сумме углов треугольника – сумма углов треугольника равна 180^о

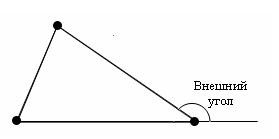
1. Сформулируйте определение внешнего угла треугольника. Сформулируйте теорему о свойстве внешнего угла треугольника.

Внешний угол треугольника – угол, смежный с каким-нибудь углом этого треугольника

Теорема о свойстве внешнего угла треугольника – внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним

1. Сформулируйте определение прямоугольного треугольника. Сформулируйте свойство прямоугольного треугольника.

Прямоугольный треугольник – это треугольник, в котором один угол прямой (то есть составляет 90 градусов)

Первое свойство прямоугольного треугольника – сумма двух острых углов прямоугольного треугольника равна 90^о

Второе свойство прямоугольного треугольника – катет прямоугольного треугольника, лежащий против угла в 30^о, равен половине гипотенузы

Третье свойство прямоугольного треугольника – если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против его катета равен 30^о

1. Сформулируйте признаки равенства прямоугольных треугольников.

Первый признак равенства прямоугольноготреугольника – если катеты одного прямоугольного треугольника равны катетам другого, то такие треугольники равны

Второй признак равенства прямоугольного треугольника – если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащего к нему острому углу другого, то такие треугольники равны

Третий признак равенства прямоугольного треугольника – если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны

Четвёртый признак прямоугольного треугольника – если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны

1. Сформулируйте теорему о зависимости между сторонами и углами треугольника.

Теорема о соотношениях между сторонами и углами треугольника –в треугольнике против большей стороны лежит больший угол; против большего угла лежит большая сторона

1. Сформулируйте свойство углов, образованных при пересечении параллельных прямых секущей.

Первое свойство – если две параллельные прямые пересечены секущей, то накрест лежащие углы равны

Второе свойство - если две параллельные прямые пересечены секущей, то соответственные углы равны

Третье свойство - если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180^о

1. Определение четырёхугольника и его элементов. Диагональ четырёхугольника. Определение выпуклого четырёхугольника. Сумма углов выпуклого четырёхугольника.

Четырёхугольник – многоугольник, состоящий из четырёх углов

Диагональ четырёхугольника – отрезок, соединяющий любые две несоседние вершины

Выпуклый четырёхугольник – четырёхугольник, лежащий по одну сторону от каждой прямой, проходящей через две его соседние вершины

Сумма углов выпуклого четырёхугольника равно 360^о

1. Определение параллелограмма. Свойства параллелограмма.

Параллелограмм – четырёхугольник, у которого противоположные стороны попарно параллельны

Первое свойство параллелограмма – в параллелограмме противоположные стороны равны и противоположные углы равны

Второе свойство параллелограмма – диагонали параллелограмма точкой пересечения делятся пополам

1. Признаки параллелограмма.

Первый признак параллелограмма – если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм

Второе признак параллелограмма –если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм

Третий признак параллелограмма – если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм

1. Определение трапеции. Виды трапеции. Свойства равнобедренной трапеции.

Трапеция – четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны

Виды трапеции: равнобедренная и прямоугольная

Первое свойство равнобедренной трапеции – у равнобедренной трапеции боковые стороны равны

Второе свойство равнобедренной трапеции – у равнобедренно трапеции углы при основании равны

1. Определение прямоугольника. Свойство прямоугольника. Признак прямоугольника.

Прямоугольник – параллелограмм, у которого все углы прямые

Свойство прямоугольника – диагонали прямоугольника равны

Признак прямоугольника – если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник

1. Определение ромба. Свойство ромба.

Ромб – параллелограмм, у которого все стороны равны

Свойство ромба – диагонали ромба взаимно перпендикулярны и делят его углы пополам

1. Определение квадрата. Свойства квадрата.

Квадрат – прямоугольник, у которого все стороны равны

Первое свойство квадрата – все углы квадрата прямые

Второе свойство квадрата – диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам

1. Понятие площади многоугольника. Единица измерения площадей. Свойства площадей. Площадь квадрата.

Площадь многоугольника – это величина той части плоскости, которую занимает многоугольник

Единицы измерения площадей: квадратный сантиметр (см²), квадратный метр (м²), квадратный миллиметр (мм²) и т. д.

Первое свойство площади – равные многоугольники имеют равные площади

Второе свойство площади – если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников

Площадь квадрата – площадь квадрата равна квадрату его стороны (S=a²)

1. Определение высоты параллелограмма. Площадь параллелограмма.

Высота параллелограмма – перпендикуляр, проведённый из любой точки противоположной стороны к прямой, содержащей основание

Площадь параллелограмма –

произведение основания на высоту

произведение сторон на синус угла между ними

полупроизведение диагоналей на синус угла между ними

1. Определение высоты трапеции. Площадь трапеции.

Высота трапеции – перпендикуляр, проведённый из любой точки одного из оснований к прямой, содержащей другое основание. Площадь трапеции – площадь трапеции равна произведению полусуммы её оснований на высоту S=_h

произведение средней линии на высоту

полупроизведение диагоналей на синус угла между ними

1. Площадь ромба (через диагонали). Площадь прямоугольника.

Площадь ромба –площадь ромба равна половине произведений его диагоналей

Площадь прямоугольника – площадь прямоугольника равна произведению его смежных сторон S=ab

1. Теорема Пифагора и обратная ей.

Теорема Пифагора – в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

c² = a² + b²

Теорема, обратная теореме Пифагора – если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный

1. Площадь прямоугольного треугольника. Теорема об отношениях площадей треугольников: с равными высотами; имеющих по равному углу.

Площадь прямоугольного треугольника – площадь прямоугольного треугольника равна половине произведения его катетов

Теорема об отношениях площадей треугольников имеющих по равному углу – если угол одного треугольника равен углу другого, то площади треугольников относятся как произведение сторон, заключающих равные углы

Теорема об отношениях площадей треугольников с равными высотами – если площади двух треугольников равны, то их площади относятся как основания

1. Определение подобных треугольников. Теоремы об отношениях периметров и площадей подобных треугольников.

Подобные треугольники – два треугольника, углы которых соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого

Теорема об отношении площади подобных треугольников – отношение площадей подобных треугольников равно квадрату коэффициента подобия

1. Первый признак подобия треугольников. Определение синуса острого угла прямоугольного треугольника.

Первый признак подобия треугольников – если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

Синус острого угла прямоугольного треугольника – это отношение противолежащего катета к гипотенузе

1. Второй признак подобия треугольников. Определение косинуса острого угла прямоугольного треугольника.

Второй признак подобия треугольников – если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны

Косинус острого угла прямоугольного треугольника - это отношение прилежащего катета к гипотенузе

1. Третий признак подобия треугольников. Определение тангенса острого угла прямоугольного треугольника.

Третий признак подобия треугольников – если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны

Тангенс острого угла прямоугольного треугольника – это отношение противолежащего катета к прилежащему катету

1. Определение средней линии треугольника. Свойство средней линии треугольника.

Средняя линия треугольника – отрезок, соединяющий середины двух его сторон

Свойство средней линии треугольника – средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны

1. Свойство высоты прямоугольного треугольника, проведённой из вершины прямого угла.

Свойство высоты прямоугольного треугольника, проведённой из вершины прямого угла – это среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой

высота в прямоугольном треугольнике, поведенная из вершины прямого угла образует два треугольника, подобных исходному. Для катетов и высоты исходного треугольника верны следующие формулы:

а , b – катеты; с – гипотенуза, а_c,b_c– проекции катетов на гипотенузу.

1. Основное тригонометрическое тождество. Значение синуса, косинуса и тангенса для углов 30^о, 45^о и 60^о.

Основное тригонометрическое тождество - для любого угла α верно утверждение: sin² α +

+cos² α = 1

.

1. Каково взаимное расположение прямой и окружности в зависимости от соотношения между радиусом окружности и расстоянием от её центра до прямой?

1 случай: d (рис. 1). Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки (пересекаются в двух точках).

2 случай: d = r (рис. 2). Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну в одной точке общую точку (пересекаются).

3 случай: d r (рис. 3). Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек (не пересекаются).

1. Какая прямая называется секущей по отношению к окружности?

Секущая–это прямая, имеющая с окружность две общие точки. Или, секущая – это прямая, пересекающая окружность в двух точках

1. Какая прямая называется касательной к окружности? Какая точка называется точкой касания прямой и окружности?

Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называетсяточкой касания прямой и окружности.

1. Сформулируйте теорему о свойстве касательной к окружности.

Свойство касательной - касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.

1. Сформулируйте теорему об отрезках касательных к окружности, проведённых из одной точки.

Отрезки касательных к окружности проведённых из одной точки - отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

1. Сформулируйте признак касательной (теорему, обратную теореме о свойстве касательной).

Признак касательной - если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то онаявляется касательной.

1. Какой угол называется центральным углом окружности? В каких случаях градусная мера центрального угла считается равной a, а в каких 360° - a?

Угол с вершиной в центре окружности называется её центральным углом. Если центральный угол меньше развернутого угла, то его градусная мера считается равной a, а если больше развернутого угла, то 360° - a.

1. Объясните, что такое дуга окружности? Как она обозначается? Чему равна градусная мера дуги? В каких случаях градусная мера дуги считается равной a, а в каких 360° - a?

Если на окружности отметить две точки, то они разделят её на две дуги. Дуга–часть окружности, расположенная между двумя точками, этой окружности. Чтобы различать эти дуги, на каждой из них отмечают промежуточную точку. Когда ясно, окакой из двух дуг идёт речь, используется обозначение без промежуточной точки.

Градусная мера дуги равна градусной мере соответствующего центрального угла, т.е. если дуга меньше полуокружности, то ее градусная мера считается равной a . Если же дуга больше полуокружности, то ее градусная мера считается равной 360° - a.Градусная мера

полуокружности равна180°.

1. Объясните, какая дуга называется полуокружностью.

Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром окружности.

1. Какой угол называется вписанным? В каком случае говорят, что вписанный угол опирается на дугу?

Вписанный угол - угол, вершина которого лежит на окружности, а стороны пересекают окружность.

1. Сформулируйте и докажите теорему о вписанном угле.

Вписанный угол измеряется половиной дуги, на которую опирается.

I случай II случай III случай

Замечание. Так как градусная мера дуги равна градусной мере соответствующего центрального угла, то теорему о вписанном угле можно сформулировать следующим образом: угол, вписанный в окружность, равен половине соответствующего центрального угла.

1. Сформулируйте и докажите теорему о вписанных углах, опирающихся на одну и ту же дугу.

Вписанные углы, опирающиеся на одну и ту же дугу, равны.

1. Сформулируйте и докажите теорему о вписанных углах, опирающихся на полуокружность.

Вписанный угол, опирающийся на полуокружность – прямой. (Вписанный угол, опирающийся на диаметр – прямой.)

1. Что такое хорда окружности? Какая хорда называется диаметром?

Диаметр - отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, называется.

Диаметр – самая большая хорда, любой диаметр – хорда, но не всякая хорда является диаметром.

1. Сформулируйте и докажите теорему об отрезках пересекающихся хорд.

Теорема: Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

Следствие: Если через данную точку S провести несколько хорд, то произведение отрезков хорды есть величина постоянное для всех хорд, т.е. SA× SB = SC× SD = SK× SL = SM× SN = … = const.

1. Чему равен угол между хордой окружности и касательной к окружности, проведённой через конец хорды?

Острый угол между хордой окружности и касательной к окружности в конце хорды равен половине угла между радиусами, проведёнными к концам хорды.

1. Каким замечательным свойством обладают медианы, высоты и биссектрисы треугольника?

Медианы, биссектрисы, высоты (или их продолжения) треугольника пересекаются в одной точке.

1. Какая окружность называется вписанной в треугольник? Какой треугольник называется описанным около окружности?

Если все стороны треугольника касаются окружности, то окружность называется вписанной в треугольник, а треугольник – описанным около этой окружности.

1. Какая окружность называется вписанной в многоугольник? Какой многоугольник называется описанным около окружности?

Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.

1. Сформулируйте теорему об окружности, вписанной в треугольник.

Теорема. В любой треугольник можно вписать окружность.

1. Сколько окружностей можно вписать в треугольник?

В треугольник можно вписать только одну окружность.

1. Какая точка является центром окружности, вписанной в треугольник?

Центром окружности, вписанной в треугольник, является точка пересечения биссектрис углов треугольника.

1. Как построить окружность, вписанную в треугольник? Можно ли вписать окружность в четырёхугольник?

1)Построить биссектрисы двух углов треугольника.

2)Точку их пересечения обозначить буквой О.

3)Из точкиОк одной из сторон треугольника провести перпендикуляр.

4)Построить окружность с центром в точкеОи радиусом, равным проведённому перпендикуляру.

5)Не во всякий четырёхугольник можно вписать окружность

1. В какой четырёхугольник можно вписать окружность?

Если суммы противоположных сторон выпуклого четырёхугольника равны, то в него можно вписать окружность.

АВ+СD=ВС+АD

1. Можно ли вписать окружность в ромб? квадрат? параллелограмм? прямоугольник? трапецию?

1. В ромбе и в квадрате все стороны равны, значит и суммы противоположных сторон равны, поэтому в любой ромб и в любой квадрат можно вписать окружность.

2. В параллелограмм только тогда можно вписать окружность, когда он будет ромбом.

3. В прямоугольник только тогда можно вписать окружность, когда он будет квадратом.

4. В трапецию можно вписать окружность тогда, когда суммы противоположных сторон будут равны.

1. Каким свойством обладают стороны четырёхугольника, описанного около окружности?

В любом описанном четырёхугольнике суммы противоположных сторон равны.

АВ+СD=ВС+АD

1. Какая окружность называется описанной около треугольника? Какой треугольник называется вписанным в окружность?

Если все вершины треугольника лежат на окружности, то окружность называется описанной около треугольника, а треугольник – вписанным в эту окружность.

1. Какая окружность называется описанной около многоугольника? Какой многоугольник называется вписанным в окружность?

Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.

1. Сформулируйте теорему об окружности, описанной около треугольника.

Теорема: Около любого треугольника можно описать окружность.

1. Сколько окружностей можно описать около данного треугольника?

Около треугольника можно описать только одну окружность.

1. Какая точка является центром окружности, описанной около треугольника?

Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к его сторонам.

1. Где находится центр окружности, описанной около остроугольного треугольника?

Центр окружности, описанной около остроугольного треугольника лежит внутри треугольника.

1. Как построить окружность, описанную около остроугольного треугольника?

1)Построить серединные перпендикуляры к двум сторонам треугольника.

2)Точку их пересечения обозначить буквой О.

3)Построить окружность с центром в точке О и радиусом, равным расстоянию от точки О до любой из вершин треугольника.

1. Где находится центр окружности, описанной около прямоугольного треугольника?

Центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы.

1. Как построить окружность, описанную около прямоугольного треугольника?

1 способ:

1)Построить серединные перпендикуляры к двум сторонам треугольника.

2)Точку их пересечения обозначить буквойО(точкаО– середина гипотенузы).

3)Построить окружность с центром в точкеОи радиусом, равным расстоянию от точкиОдо любой из вершин треугольника.

2 способ:

1)Построить точкуО–середину гипотенузы.

2)Построить окружность с центром в точке О и радиусом, равным половине гипотенузы.

1. Где находится центр окружности, описанной около тупоугольного треугольника?

Центр окружности, описанной около тупоугольного треугольника, лежит вне треугольника.

1. Как построить окружность, описанную около тупоугольного треугольника?

1)Построить серединные перпендикуляры к двум сторонам треугольника.

2)Точку их пересечения обозначить буквойО(точкаОлежит вне треугольника).

3)Построить окружность с центром в точкеОи радиусом, равным расстоянию от точкиОдо любой из вершин треугольника.

1. Можно ли описать окружность около четырёхугольника?

Около четырёхугольника не всегда можно описать окружность.

1. В каком случае около четырёхугольника можно описать окружность?

Если сумма противоположных углов четырёхугольника равна 180^о, то около него можно описать окружность.

1. Можно ли описать окружность около ромба? квадрата? параллелограмма? прямоугольника? трапеции?

Так как в квадрате и в прямоугольнике все углы равны по 90^о, значит сумма противоположных углов равна180^о, поэтому около любого квадрата и около любого прямоугольника можно описать окружность.

Около ромба только тогда можно описать окружность, когда он будет квадратом.

Около параллелограмма тогда можно описать окружность, когда он будет прямоугольником.

Около трапеции можноописать окружность, если она равнобедренная, так как только вэтом случае сумма противоположных углов равна 180^о.

1. Каким свойством обладают углы четырёхугольника, вписанного в окружность?

В любом вписанном четырёхугольнике сумма противоположных углов равна 180^о.

1. В какой четырёхугольник всегда можно вписать окружность и можно описать около него окружность?

В квадрат всегда можно вписать окружность, и всегда можно описать окружность около него.

1. Какие точки называют замечательными точками треугольника?

С каждым треугольником связаны четыре точки:

1)точка пересечения медиан - центроид треугольника (центр масс однородной треугольной пластинки);

2)точка пресечения биссектрис - центр окружности, вписанной в треугольник;

3) точка пересечения серединных перпендикуляров - центр окружности, описанной около треугольника;

4) точка пересечения высот (или их продолжений) – ортоцентр треугольника.

Эти четыре точки называют замечательными точками треугольника.

23