Россия,
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 24.04.2024 07:04
Захарова Екатерина Александровна
Учитель математики
1 542
32 882 
Местоположение
Специализация
Урок на тему: "Модуль числа"
Категория:
Математика
27.12.2016 15:23
Просмотр содержимого документа
«Урок на тему: "Модуль числа"»
На этом уроке мы поговорим о том, что число состоит из знака и количества. Кроме того, введём понятие модуля числа, которое будет обозначать количество, без учёта знака числа. Также обсудим свойства модуля и как с ним работать.
Введение
Положительные числа, натуральные, а затем и дробные мы ввели для указания количества: 
дерева, 
литра молока (рис. 1).
Рис. 1. Пример использования положительных чисел
Затем мы ввели отрицательные числа: например, 
. Теперь число, кроме количества, содержит еще и знак, который указывает, что нужно делать с этим количеством – добавить или отнять. То есть после того, как были введены отрицательные числа, мы можем сказать, что любое число состоит из количества (реально существующего) и знака (придуманного нами для упрощения записи арифметических действий).
Но иногда бывает важна только одна характеристика – количество, а знак нас не интересует.
Модуль числа
Рассмотрим такой пример. Для таксиста важно, какой длины путь он преодолевает с пассажиром (рис. 2).
Рис. 2. Километраж
Ведь, если в конце поездки пассажира привозят обратно домой, это не означает, что он ничего таксисту не должен, так как он проехал какое-то расстояние с начала поездки (рис. 3).
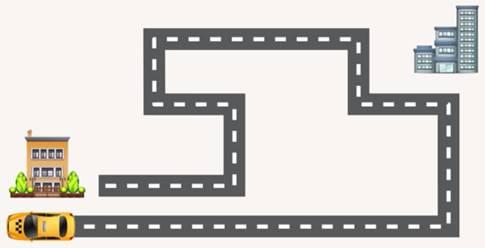
Рис 3. Путь, проделанный такси
Пусть теперь такси может ездить только вдоль прямой (вправо или влево). У нас уже есть подходящая модель – координатная прямая (рис. 4).
Рис. 4. Аналогия с координатной прямой
Предположим, клиенты проехали 
км влево, затем 
км вправо, затем ещё 
км вправо, затем ещё км влево. В результате автомобиль отъехал на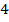 
км влево от исходной точки: 
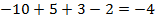(рис. 5).
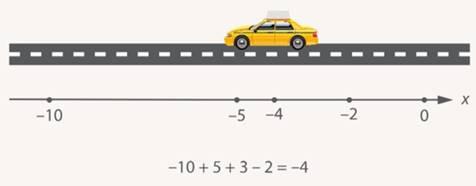
Рис. 5. Сколько проехала машина (считаем с помощью числовой прямой)
Но ведь путь, который проделало такси, значительно больше: 
км.
Для подсчёта пути мы складывали только количества, без учёта знака.
Ту часть числа, которая указывает на количество, называют абсолютным значением (или модулем числа). То есть можно сказать и так: любое число состоит из знака и абсолютного значения (модуля). Если знак плюс, то для краткости его обычно не пишут.
Например, у числа 
знак минус и модуль , у числа , знак плюс и модуль (рис. 6).
Рис. 6. Из чего состоят противоположные числа
Пример: машина проехала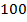 
км по дороге. Используем для этой ситуации математическую модель – числовую прямую. Машина из точки 
могла двигаться вправо или влево. Можно так и говорить: перемещение на 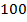км вправо, перемещение на 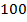км влево. Но у нас есть удобный инструмент, отрицательные числа. Поэтому короче мы можем говорить так: перемещение 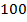или перемещение 
(рис. 7).
Рис. 7. Возможные движения машины
Перемещение было разное, но удалился автомобиль от начальной точки (от ) на одно и то же расстояние – на 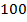км. Но 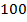– это и есть модуль (как для числа , так и для ).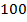
То есть про модуль числа можно сказать и так: модуль – это расстояние от числа до нуля (на самом деле это определение более универсальное, но об этом вы узнаете в старших классах).
Перемещение и путь
В физике два этих понятия так и называют:
перемещение: для него важен результат – где были и где оказались в итоге;
путь: здесь важно расстояние, которое мы прошли, и не важно, где мы оказались в итоге.
Так, если машина, двигалась из точки вправо 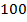км, а потом влево 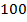км, то она вернется в начальную точку. Перемещение равно , но путь равен 
км (рис. 8).
Рис. 8. Перемещение и путь
Перемещение и путь на плоскости
Перемещение от одной точки до другой изображают отрезком со стрелкой. Называют его вектором (рис. 1).
Рис. 9. Вектор
Здесь ситуация как с числами: есть количественная часть (длина) и есть направление (у числа их было всего два (
и 
), а здесь направлений может быть бесконечно много).
Сам вектор обозначают со стрелкой сверху. Длину вектора называют модулем (помните, как и у числа: модуль – это количественная часть) и обозначают с прямыми скобками или просто как отрезок (рис. 2).
Рис. 10. Обозначение вектора и его длины
Если нам нужно попасть из одной точки в другую, мы не всегда можем пройти по прямой. Например, из точки 
мы движемся в точку 
, обходя газон, по которому ходить запрещено. То есть мы переместились два раза 
и
. Итоговое перемещение 
(рис. 3).
Рис. 11. Перемещение
Перемещение – это сумма двух перемещений 
: 
. Для путей это не верно. Длина отрезка 
меньше суммы длин отрезков 
и 
: 
. Путь по прямой короче, чем в обход.
Все это можно записать одним неравенством: 
. Оно означает вот что: сумма двух перемещений – это итоговое перемещение. Его длина меньше, чем сумма длин каждого перемещения по отдельности: 
.
Подумайте, может ли здесь быть равенство, если по-другому будут расположены векторы перемещения? А противоположный знак, то есть знак 
?
Рассмотрим такой пример. Человек гуляет с собакой, он движется из точки в точку по прямой, при этом собака движется еще из стороны в сторону, насколько позволяет поводок (рис. 4).
Рис. 12. Иллюстрация к примеру
Перемещение человека (рис. 5).
Рис. 13. Перемещение человека
Перемещение собаки складывается из кусочков и тоже в итоге равно (рис. 6).
Рис. 14. Перемещение собаки
Но если складывать не перемещения, а пути, т.е. не векторы, а их модули, то окажется, что собака пробежала путь, в два или три раза больший. Собака, совершая одинаковое перемещение с хозяином, могла пробежать и в , и в 
раз больший путь, все ограничивается ее активностью.
Есть такая задача: измерение длины береговой линии. С перемещением от точки до точки вдоль берега все понятно. Это вектор (рис. 7).
Рис. 15. Перемещение
А вот путь складывается из кусочков (рис. 8). Тут вроде бы как с собакой: нужно сложить модули таких перемещений, векторов.
Рис. 16. Кусочки пути
Но если смотреть более точно, каждое такое перемещение складывается из еще более мелких перемещений. Путь сильно возрастает (рис. 9).
Рис. 17. Возрастание пути
Но это еще не все: если смотреть еще более точно, то и они делятся на маленькие перемещения. Береговая линия все более и более изрезана (рис. 10). И это никогда не заканчивается.
Рис. 18. Изрезанная береговая линия
То есть длину береговой линии не получается точно измерить таким образом.
Вот так получается, что, не отходя далеко от общего вектора перемещения, можно получить очень большой (как путь собаки) или даже бесконечный путь (как береговая линия).
Определение модуля
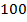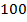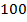Модуль числа договорились обозначать вертикальными скобками. Итак, модуль положительного числа равен самому числу , модуль отрицательного числа тоже равен , то есть противоположному числу: 
, 
.
Остался вопрос: чему равен модуль нуля? Расстояние от нуля до нуля равно нулю. Поэтому модуль нуля считать равным нулю: 
.
Итак, мы уже все знаем, чтобы дать более точное определение, что такое модуль числа.
Модуль числа – это число, равное ему самому, если число положительное, противоположному числу, если оно отрицательное, и все равно какому (самому или противоположному), если число равно нулю. Пусть будет самому: .
Чтобы запись была короче, объединим первую и третью строчки. И определение теперь звучит так: модуль числа равен самому числу, если оно неотрицательное (положительное или ноль), и противоположному числу, если оно отрицательное: 
.
Это определение не объясняет суть, что такое модуль. Но мы про суть уже поговорили раньше. Оно является удобным инструментом для выполнения арифметических действий. Особенно пригодится это определение, когда мы будем решать уравнения с модулем.
Если отвлечься от задач про путь и перемещение, то нахождения модуля интересно еще вот чем. Раньше мы выполняли операции с двумя или несколькими числами. Например, брали два числа, складывали их, получали новое число, сумму: 
. Или сравнивали два числа: 
.
Модуль же – это операция с одним числом. Берем одно число и находим для него другое число – модуль: 
. Сходная ситуация была при округлении чисел, хотя сам смысл процедуры там был совсем другой: 
.
Примеры
Итак, мы обсудили, что такое модуль, для чего он нужен, дали ему точное определение. Теперь перейдем к технике вычислений. Потренируемся этот модуль находить.
Для того чтобы найти модуль числа, необязательно изображать число на координатной прямой и измерять расстояние до нуля. Чтобы найти модуль числа, нужно просто не обращать внимания на знак числа: 
. То есть даже определение модуля нам пока не очень понадобится. Нужно просто записывать число без знака. Таким образом, у противоположных чисел модули равны: 
.
Решим несколько примеров на нахождение модуля.
Модуль переменной величины
Как быть с модулем переменной величины? Про нее мы можем не знать, отрицательная она или положительная. Она может быть равна и нулю. Что нам известно про её модуль в такой ситуации? Мы не можем утверждать, что модуль 
равен самому числу . Ведь может оказаться, что отрицательно, но модуль не может быть отрицательным.
Рассмотрим противоположное число 
. Знак минус перед не означает, что оно отрицательно. Поэтому с модулем этого числа тоже нет определенности.
Что мы знаем наверняка, так это, что модули этих двух чисел равны друг другу. И этот модуль равен одному из этих чисел, тому, которое неотрицательно: 
или 
.
Заключение
Итак, подведем итог.
Модуль числа – это расстояние от числа до нуля (рис. 9).
Рис. 19. Модуль числа
Чтобы найти модуль числа, нужно записать это число без учета знака (рис. 10).
Рис. 20. Как найти модули
Модули противоположных чисел равны (рис. 11).
Рис. 21. Модули противоположных чисел
Точное определение модуля выглядит так:модуль числа равен самому числу, если оно неотрицательное (положительное или ноль), и противоположному числу, если оно отрицательное (рис. 12).
Рис. 22. Определение модуля
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
