Точки экстремума функции и их нахождение.

Точки экстремума функции и их нахождение

«Применение производной для исследования функций на монотонность и экстремумы»

Выполнила учитель математики Григорьева С.В.

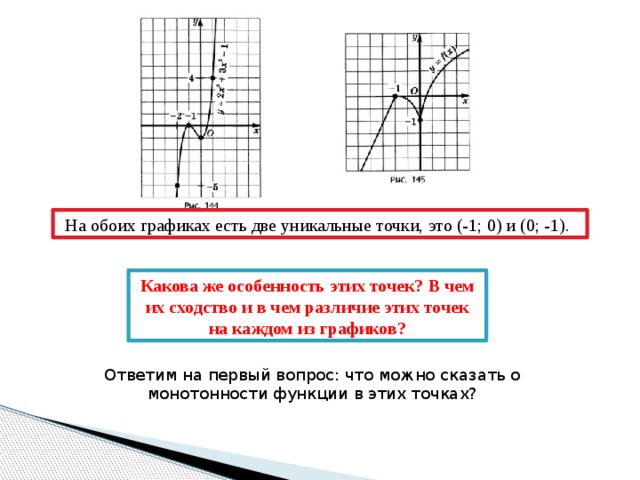
На обоих графиках есть две уникальные точки, это (-1; 0) и (0; -1).

Какова же особенность этих точек? В чем их сходство и в чем различие этих точек на каждом из графиков?

Ответим на первый вопрос: что можно сказать о монотонности функции в этих точках?

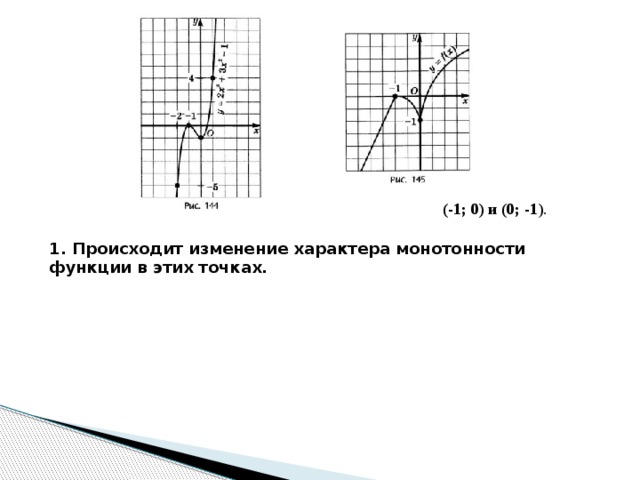
(-1; 0) и (0; -1 ).

1. Происходит изменение характера монотонности функции в этих точках.

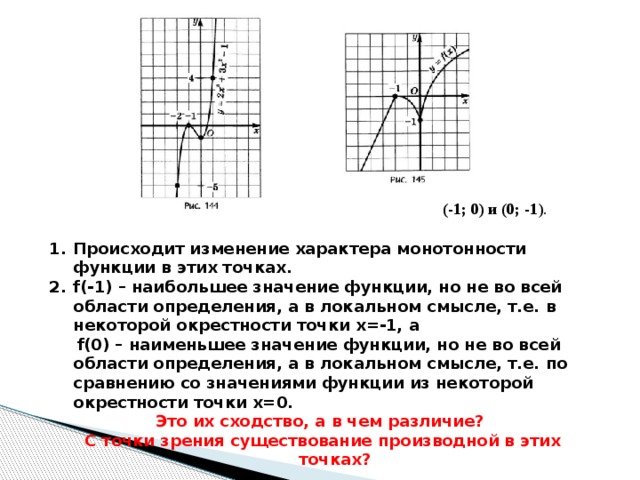
(-1; 0) и (0; -1 ).

• Происходит изменение характера монотонности функции в этих точках.
• f(-1) – наибольшее значение функции, но не во всей области определения, а в локальном смысле, т.е. в некоторой окрестности точки x=-1, а

f(0) – наименьшее значение функции, но не во всей области определения, а в локальном смысле, т.е. по сравнению со значениями функции из некоторой окрестности точки х=0.

Это их сходство, а в чем различие?

С точки зрения существование производной в этих точках?

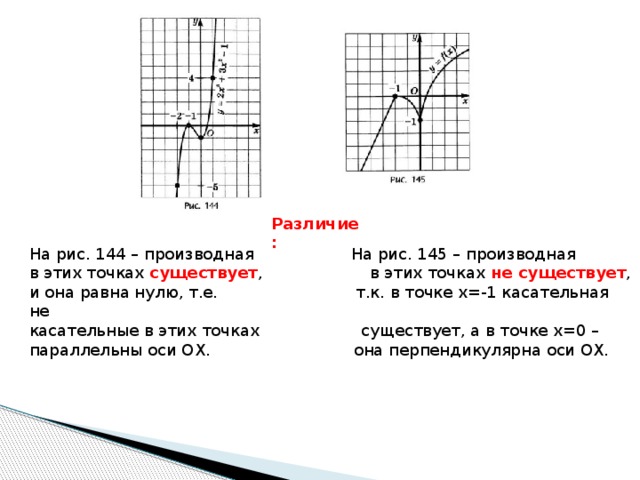
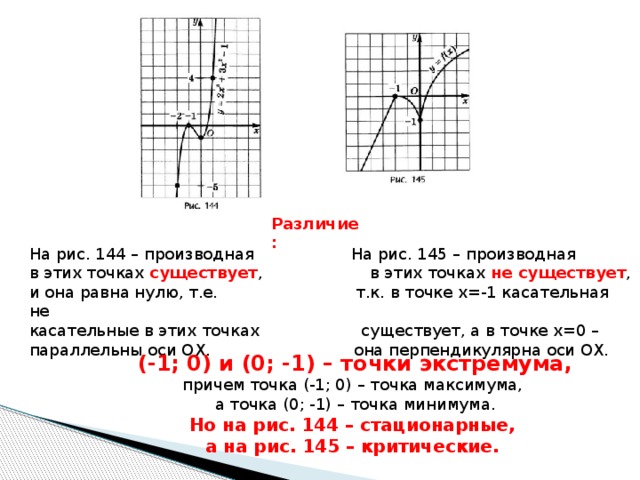
Различие:

На рис. 144 – производная На рис. 145 – производная

в этих точках существует , в этих точках не существует ,

и она равна нулю, т.е. т.к. в точке х=-1 касательная не

касательные в этих точках существует, а в точке х=0 –

параллельны оси ОХ. она перпендикулярна оси ОХ.

Различие:

На рис. 144 – производная На рис. 145 – производная

в этих точках существует , в этих точках не существует ,

и она равна нулю, т.е. т.к. в точке х=-1 касательная не

касательные в этих точках существует, а в точке х=0 –

параллельны оси ОХ. она перпендикулярна оси ОХ.

(-1; 0) и (0; -1) – точки экстремума,

причем точка (-1; 0) – точка максимума,

а точка (0; -1) – точка минимума.

Но на рис. 144 – стационарные,

а на рис. 145 – критические.

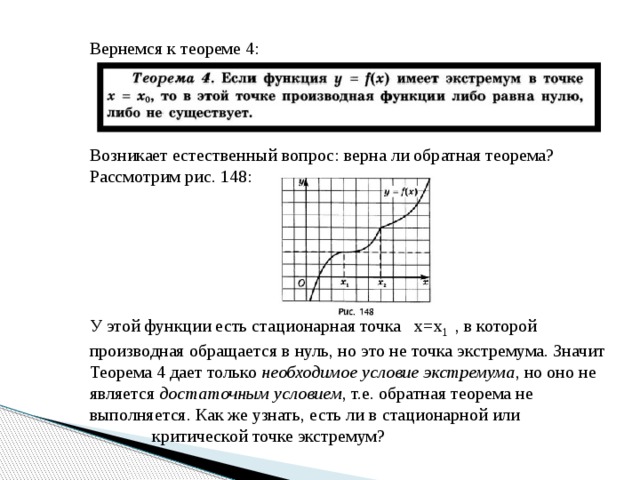
Вернемся к теореме 4:

Возникает естественный вопрос: верна ли обратная теорема?

Рассмотрим рис. 148:

У этой функции есть стационарная точка х=х 1 , в которой производная обращается в нуль, но это не точка экстремума. Значит Теорема 4 дает только необходимое условие экстремума , но оно не является достаточным условием , т.е. обратная теорема не выполняется. Как же узнать, есть ли в стационарной или

критической точке экстремум?