Дата проведения:
Тема урока: Примеры применения производной к исследованию функции.
Цели урока: 1) Закрепить знания нахождения промежутков возрастания и убывания функции, экстремумов функции с помощью производной;
2) Способствовать выработке навыка построения графика функции исследованием с помощью производной.
Задачи урока:
Учебная: Повторить:
1) Признаки возрастания и убывания функции;
2) Определение критических точек, точек экстремума;
3) Признаки максимума и минимума
4) Теорему о монотонности функции.
Развивающая: Учить осуществлять исследовательскую деятельность.
Воспитательная: Формировать навыки умственного труда.
Тип урока: Урок комплексного применения ЗУН учащихся.
Оборудование и источники информации: Учебник, рисунки.
Ход урока.
- Орг.момент
Приветствие, сообщение темы урока и цели.
2. Актуализация ЗУН.
Повторение:
1) Признаки возрастания и убывания функции:
Если  в каждой точке интервала
в каждой точке интервала 
 , то функция f возрастает на
, то функция f возрастает на  .
.
Если  в каждой точке интервала I, то функция f убывает на I.
в каждой точке интервала I, то функция f убывает на I.
2) Определение критических точек:
Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называются критическими точками этой функции.
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках – экстремумами.
3) Признаки максимума и минимума:
Если функция f непрерывна в точке х0 , а  на интервале (а;х0) и
на интервале (а;х0) и  на интервале (х0;в), то х0 является точкой максимума функции f.
на интервале (х0;в), то х0 является точкой максимума функции f.
Если функция f непрерывна в точке х0 , а  на интервале (а;х0) и
на интервале (а;х0) и  на интервале (х0;в), то х0 является точкой минимума функции f.
на интервале (х0;в), то х0 является точкой минимума функции f.
3. Работа с учебником.
При построении графика функции с помощью производной полезно придерживаться такого плана:
1) Найти область определения функции.
2) Выяснить, является ли функция четной или нечетной, периодической.
3) Определить точки пересечения графика функции с координатными осями, если это возможно.
4) Найти критические точки функции.
5) Определить промежутки монотонности и экстремумы функции.
6) Используя результаты исследования, соединить полученные точки плавной кривой.
Иногда для большей точности находят несколько дополнительных точек; их координаты вычисляют, пользуясь уравнением кривой.
Этот план исследования функции и построения ее графика является примерным, его не всегда надо придерживаться пунктуально: можно менять порядок пунктов, некоторые совсем опускать, если они не подходят к данной функции. В частности, если нахождение точек пересечения с осями координат связано с большими трудностями, то это можно не делать.
Если функция четная, то ее график симметричен относительно оси Оy, поэтому достаточно построить график для положительных значений аргумента, принадлежащих области определения и так далее.
4. Устная работа.
Назовите по следующим данным промежутки возрастания, убывания и точки максимума и минимума.
1.
|
х
|
(-7;1)
|
1
|
(1;6)
|
6
|
(6;7)
|
|

|
+
|
0
|
-
|
0
|
+
|
|
f(x)
|
|
10
|
|
-3
|
|
5.Новая тема
Учитывая все сказанное, исследуем функцию: f(x)= 3x5-5х3+2 и построим ее график.
Проведем исследование по указанной схеме:
D (f ') =IR, так как f (x) - многочлен.
Функция f не является ни четной, ни нечетной, так как
f (-x)= 3(-x)5-5(-x)3+2 = -3x 5+5х3+2= -( 3x5-5х3-2) 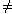 f(x)
f(x)
Найдем координаты точек пересечения графика с осями координат:
а) с осью 0Х, для этого решим уравнение: 3x5-5х3+2 = 0.
Методом подбора можно найти один из корней (x = 1). Другие корни могут быть найдены только приближенно. Поэтому для данной функции остальные точки пересечения графика с осью абсцисс и промежутки знака постоянства находить не будем.
б) с осью 0У: f(0)=2
Точка А (0; 2) - точка пересечения графика функции с осью 0У.
Отметили, что промежутки знака постоянства не будем находить.
Найдем промежутки возрастания и убывания функции
а ) f '(x)= 15x4 -15х2 = 15х2 (х2-1)
D (f ') =IR, поэтому критических точек которых f '(x)не существует, нет.
б) f '(x) = 0, если х2(х2-1)=0 <=> x = -1 V x = 0 V x = 1.
в) Получим три критические точки, они разбивают координатную прямую на четыре промежутка. Определим знак производной на этих промежутках:

Из рисунка видно, что: f возрастает на интервалах (- ; -1) и (1; +
; -1) и (1; + );
);
f убывает на (-1 ; 0) и (0; 1).
Так как функция непрерывна в точках -1; 0; 1, то f возрастает на (- ; -1] и [1; +
; -1] и [1; + );
);
f убывает на [-1; 0] и [0; 1].
6. Найдем точки экстремума функции и вычислим значения функции в этих точках. Рассматривая рисунок знаков f ?видим, что:
x =-1 - точка max, f (-1) =4;
x = 1 - точка min, f (1) =0.
6. Закрепление. Выполнение упр №296

7. Подведение итога.
-по какому плану необходимо исследовать функцию?
-как определить к промежутки возр.и убыв.функции?
Дом/задание №296(г)
Просмотр содержимого документа
«Примеры применения производной к исследованию функции.»
Дата проведения:
Тема урока: Примеры применения производной к исследованию функции.
Цели урока: 1) Закрепить знания нахождения промежутков возрастания и убывания функции, экстремумов функции с помощью производной;
2) Способствовать выработке навыка построения графика функции исследованием с помощью производной.
Задачи урока:
Учебная: Повторить:
1) Признаки возрастания и убывания функции;
2) Определение критических точек, точек экстремума;
3) Признаки максимума и минимума
4) Теорему о монотонности функции.
Развивающая: Учить осуществлять исследовательскую деятельность.
Воспитательная: Формировать навыки умственного труда.
Тип урока: Урок комплексного применения ЗУН учащихся.
Оборудование и источники информации: Учебник, рисунки.
Ход урока.
Орг.момент
Приветствие, сообщение темы урока и цели.
2. Актуализация ЗУН.
Повторение:
1) Признаки возрастания и убывания функции:
Если  в каждой точке интервала
в каждой точке интервала 
 , то функция f возрастает на
, то функция f возрастает на  .
.
Если  в каждой точке интервала I, то функция f убывает на I.
в каждой точке интервала I, то функция f убывает на I.
2) Определение критических точек:
Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называются критическими точками этой функции.
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках – экстремумами.
3) Признаки максимума и минимума:
Если функция f непрерывна в точке х0 , а  на интервале (а;х0) и
на интервале (а;х0) и  на интервале (х0;в), то х0 является точкой максимума функции f.
на интервале (х0;в), то х0 является точкой максимума функции f.
Если функция f непрерывна в точке х0 , а  на интервале (а;х0) и
на интервале (а;х0) и  на интервале (х0;в), то х0 является точкой минимума функции f.
на интервале (х0;в), то х0 является точкой минимума функции f.
3. Работа с учебником.
При построении графика функции с помощью производной полезно придерживаться такого плана:
1) Найти область определения функции.
2) Выяснить, является ли функция четной или нечетной, периодической.
3) Определить точки пересечения графика функции с координатными осями, если это возможно.
4) Найти критические точки функции.
5) Определить промежутки монотонности и экстремумы функции.
6) Используя результаты исследования, соединить полученные точки плавной кривой.
Иногда для большей точности находят несколько дополнительных точек; их координаты вычисляют, пользуясь уравнением кривой.
Этот план исследования функции и построения ее графика является примерным, его не всегда надо придерживаться пунктуально: можно менять порядок пунктов, некоторые совсем опускать, если они не подходят к данной функции. В частности, если нахождение точек пересечения с осями координат связано с большими трудностями, то это можно не делать.
Если функция четная, то ее график симметричен относительно оси Оy, поэтому достаточно построить график для положительных значений аргумента, принадлежащих области определения и так далее.
4. Устная работа.
Назовите по следующим данным промежутки возрастания, убывания и точки максимума и минимума.
1.
| х | (-7;1) | 1 | (1;6) | 6 | (6;7) |
| 
| + | 0 | - | 0 | + |
| f(x) |
| 10 |
| -3 |
|
5.Новая тема
Учитывая все сказанное, исследуем функцию: f(x)= 3x5-5х3+2 и построим ее график.
Проведем исследование по указанной схеме:
D (f ') =IR, так как f (x) - многочлен.
Функция f не является ни четной, ни нечетной, так как
f (-x)= 3(-x)5-5(-x)3+2 = -3x 5+5х3+2= -( 3x5-5х3-2)  f(x)
f(x)
Найдем координаты точек пересечения графика с осями координат:
а) с осью 0Х, для этого решим уравнение: 3x5-5х3+2 = 0.
Методом подбора можно найти один из корней (x = 1). Другие корни могут быть найдены только приближенно. Поэтому для данной функции остальные точки пересечения графика с осью абсцисс и промежутки знака постоянства находить не будем.
б) с осью 0У: f(0)=2
Точка А (0; 2) - точка пересечения графика функции с осью 0У.
Отметили, что промежутки знака постоянства не будем находить.
Найдем промежутки возрастания и убывания функции
а ) f '(x)= 15x4 -15х2 = 15х2 (х2-1)
D (f ') =IR, поэтому критических точек которых f '(x)не существует, нет.
б) f '(x) = 0, если х2(х2-1)=0 x = -1 V x = 0 V x = 1.
в) Получим три критические точки, они разбивают координатную прямую на четыре промежутка. Определим знак производной на этих промежутках:

Из рисунка видно, что: f возрастает на интервалах (- ; -1) и (1; +
; -1) и (1; + );
);
f убывает на (-1 ; 0) и (0; 1).
Так как функция непрерывна в точках -1; 0; 1, то f возрастает на (- ; -1] и [1; +
; -1] и [1; + );
);
f убывает на [-1; 0] и [0; 1].
6. Найдем точки экстремума функции и вычислим значения функции в этих точках. Рассматривая рисунок знаков f ?видим, что:
x =-1 - точка max, f (-1) =4;
x = 1 - точка min, f (1) =0.
6. Закрепление. Выполнение упр №296

7. Подведение итога.
-по какому плану необходимо исследовать функцию?
-как определить к промежутки возр.и убыв.функции?
Дом/задание №296(г)






 в каждой точке интервала
в каждой точке интервала 
 , то функция f возрастает на
, то функция f возрастает на  в каждой точке интервала I, то функция f убывает на I.
в каждой точке интервала I, то функция f убывает на I. на интервале (а;х0) и
на интервале (а;х0) и  на интервале (а;х0) и
на интервале (а;х0) и 
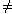 f(x)
f(x)
 ; -1) и (1; +
; -1) и (1; +



















