Тема Урока. Применение производной в решении прикладных задач .
В математике следует помнить не формулы, а процессы мышления.
Решение прикладных задач часто сводится к нахождению наибольшего и наименьшего значений непрерывности на отрезке функций.
Что нужно сделать, чтобы найти наибольшее и наименьшее значения функции, имеющей на отрезке конечное число критических точек? (Чтобы найти на отрезке наибольшее и наименьшее значения функции, имеющей на отрезке конечное число критических точек, нужно вычислить значения функции во всех критических точках и на концах отрезка, а затем из полученных чисел выбрать наибольшее и наименьшее. Изложенный выше метод поиска наибольших и наименьших значений функции применяют при решении разнообразных прикладных задач).
Какие действия нужно совершить, чтобы решить задачу прикладного характера? Перевести задачу на язык функций. Для этого выбрать удобный параметр (х), через который интересующую нас величину выражаем как функцию f(x); средствами анализа ищем наибольшее и наименьшее значение этой функции на некотором промежутке; выясняем, какой практический смысл (в терминах первоначальной задачи) имеет полученный (на языке функций) результат.
Выделите, основные этапы, при решении задач прикладного характера:
- формализация;
- решение полученной математической задачи;
- интерпретация найденного решения.
3. Решение заданий, направленных на окончательное решение учебной задачи.
Задача. Буровая вышка расположена в поле в 9км от ближайшей точки шоссе. С буровой надо направить курьера в пункт, расположенный по шоссе в 15 км от упомянутой точки (считаем шоссе прямолинейным). Скорость курьера на велосипеде по полю 8 км/ч, а по шоссе 10 км/ч. К какой точке шоссе ему надо ехать, чтобы в кратчайшее время достичь пункта?
Методика работы с задачей. Скажите, часто ли такие задачи приходиться решать в жизни? Каким способом, можно решить предложенную задачу? (Идет анализ текста задачи и ее перевод в язык функций)
Предлагаю, проанализировать условие задачи:
- На каком расстоянии находится буровая вышка от ближайшей точки шоссе?
- На каком расстоянии находятся друг от друга ближайшая точка от буровой вышки и пункт, куда надо отправить курьера?
- Известна ли скорость курьера на велосипеде по полю?
- Известна ли скорость курьера на машине по шоссе?
- Известно ли, к какой точке шоссе надо ехать, чтобы достичь нужный пункт в кратчайшее время?
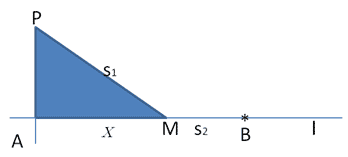
Следующим этапом работы является составление мысленной модели задачи в виде схематического рисунка к задаче, и вводятся условные обозначения: Р – буровая вышка; В – населенный пункт, l – шоссе, РМВ – маршрут следования курьера.
Установите, какие величины будут постоянными, а какие – переменными?
Постоянные величины – РА, АВ, vп, vш
Переменные величины – АМ, МВ, РМ
Исследуемая величина – время, за которое курьеру надо доехать до нужного пункта.
Чему равны постоянные величины: РА = 9 км, АВ = 15 км.vп = 8 км/ч, vш = 10 км/ч
На этапе математического моделирования выбираем параметр (х), через который выражаем интересующую нас величину как t(x):
1. Пусть x – расстояние АМ, 0 < x < 15;
2. Знание, какой теоремы нам потребуется, чтобы из прямоугольного треугольника выразить РМ? (Теорема Пифагора). Из прямоугольного треугольника РАМ выражаем:
S1 = РМ =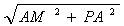 =
=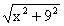 ; S2 = МВ = 15 – х;
; S2 = МВ = 15 – х;
3. Согласно условию получаем: путь S1 (по полю), который курьер проходит со скоростью v = 8 км/ч, а путь S2 (по шоссе) – со скоростью v = 10 км/ч.;
4. Вспомните формулу нахождения пути (расстояния) из курса физики и из этой формулы выразите время (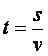 ). Значит курьер проезжает на велосипеде по полю путь S1 за время t1 =.
). Значит курьер проезжает на велосипеде по полю путь S1 за время t1 =.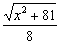 ; а на велосипеде по шоссе путь S2 за время t2 =
; а на велосипеде по шоссе путь S2 за время t2 =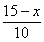 ; Тогда время, затраченное на путь S1 и S2,: t(x) =
; Тогда время, затраченное на путь S1 и S2,: t(x) = 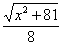 +
+ 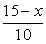
По условию задачи, средствами анализа ищем наименьшие значение функции на отрезке [0;15]. Выполняем решение задачи внутри математической модели, применяя умения решать уравнения, использовать формулы дифференцирования и находить критические точки и наибольшие или наименьшие значение функции на заданном промежутке.
1. Находим производную функции: 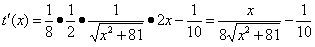
2. Находим критические точки t'(x) = 0; 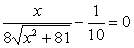
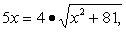 25x2 = 16 . (x2 + 81),
9x2 = 16 . 81,
9x2 = 1296,
x2 = 1296 : 9,
x2 = 144,
x1 = 12,
x2 = – 12
25x2 = 16 . (x2 + 81),
9x2 = 16 . 81,
9x2 = 1296,
x2 = 1296 : 9,
x2 = 144,
x1 = 12,
x2 = – 12
Делаем вывод:
- точку x2проверять не будем, т.к. она не принадлежит промежутку [0;15].
Находим значение функции в точках x = 0, x = 12, x = 15;
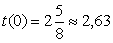 ;
t(15) ~ 2,9;
t(12) ~ 2,18
;
t(15) ~ 2,9;
t(12) ~ 2,18
- функция t(x) достигает наименьшего значения в точке x = 12
15 – 12 = 3 км
Критическое осмысление полученного результата, удержание цели занятия и условия задачи позволяет поддерживать высокий уровень активности на протяжении всего занятия. Важным этапом, является интерпретации полученного решения и поиск практического применения.
В какую точку шоссе необходимо ехать, чтобы в кратчайшие время достичь пункта назначения? (Курьеру надо ехать в точку, удаленную на 3 км от населенного пункта и на 12 км от шоссе, чтобы в кратчайшее время достичь населенного пункта.)
Какое практическое значение имеет полученный результат?
Возможно, ли применить полученный опыт использования производной в повседневной жизни, в профессиональной деятельности? (Производная выступает как инструмент изучения интенсивности изменения некоторых экономических объектов (процессов); базовые законы теории производства и потребления, спроса и предложения оказываются прямыми следствиями математических теорем).
Литература:
- Н.В.Богомолов, Практические задания по математике: учебное пособие для техникумов, М: Высш.шк.990
- А.Н.Колмогороа, А.М.Абрамов и др, Алгебра и начала анализа , учебник для 10-11 классов общеобразовательных учреждений, Москва «Просвещение», 2003
- Н.В.Богомолов, П.И.Самойленко Математика, учеб.для ССУЗзов М:Дрофа, 2008
Просмотр содержимого документа
«Тема Урока. Применение производной в решении прикладных задач .»
Тема Урока. Применение производной в решении прикладных задач .
В математике следует помнить не формулы, а процессы мышления.
Решение прикладных задач часто сводится к нахождению наибольшего и наименьшего значений непрерывности на отрезке функций.
Что нужно сделать, чтобы найти наибольшее и наименьшее значения функции, имеющей на отрезке конечное число критических точек? (Чтобы найти на отрезке наибольшее и наименьшее значения функции, имеющей на отрезке конечное число критических точек, нужно вычислить значения функции во всех критических точках и на концах отрезка, а затем из полученных чисел выбрать наибольшее и наименьшее. Изложенный выше метод поиска наибольших и наименьших значений функции применяют при решении разнообразных прикладных задач).
Какие действия нужно совершить, чтобы решить задачу прикладного характера? Перевести задачу на язык функций. Для этого выбрать удобный параметр (х), через который интересующую нас величину выражаем как функцию f(x); средствами анализа ищем наибольшее и наименьшее значение этой функции на некотором промежутке; выясняем, какой практический смысл (в терминах первоначальной задачи) имеет полученный (на языке функций) результат.
Выделите, основные этапы, при решении задач прикладного характера:
формализация;
решение полученной математической задачи;
интерпретация найденного решения.
3. Решение заданий, направленных на окончательное решение учебной задачи.
Задача. Буровая вышка расположена в поле в 9км от ближайшей точки шоссе. С буровой надо направить курьера в пункт, расположенный по шоссе в 15 км от упомянутой точки (считаем шоссе прямолинейным). Скорость курьера на велосипеде по полю 8 км/ч, а по шоссе 10 км/ч. К какой точке шоссе ему надо ехать, чтобы в кратчайшее время достичь пункта?
Методика работы с задачей. Скажите, часто ли такие задачи приходиться решать в жизни? Каким способом, можно решить предложенную задачу? (Идет анализ текста задачи и ее перевод в язык функций)
Предлагаю, проанализировать условие задачи:
На каком расстоянии находится буровая вышка от ближайшей точки шоссе?
На каком расстоянии находятся друг от друга ближайшая точка от буровой вышки и пункт, куда надо отправить курьера?
Известна ли скорость курьера на велосипеде по полю?
Известна ли скорость курьера на машине по шоссе?
Известно ли, к какой точке шоссе надо ехать, чтобы достичь нужный пункт в кратчайшее время?

Следующим этапом работы является составление мысленной модели задачи в виде схематического рисунка к задаче, и вводятся условные обозначения: Р – буровая вышка; В – населенный пункт, l – шоссе, РМВ – маршрут следования курьера.
Установите, какие величины будут постоянными, а какие – переменными?
Постоянные величины – РА, АВ, vп, vш
Переменные величины – АМ, МВ, РМ
Исследуемая величина – время, за которое курьеру надо доехать до нужного пункта.
Чему равны постоянные величины: РА = 9 км, АВ = 15 км.vп = 8 км/ч, vш = 10 км/ч
На этапе математического моделирования выбираем параметр (х), через который выражаем интересующую нас величину как t(x):
1. Пусть x – расстояние АМ, 0 x 15;
2. Знание, какой теоремы нам потребуется, чтобы из прямоугольного треугольника выразить РМ? (Теорема Пифагора). Из прямоугольного треугольника РАМ выражаем:
S1 = РМ = =
= ; S2 = МВ = 15 – х;
; S2 = МВ = 15 – х;
3. Согласно условию получаем: путь S1 (по полю), который курьер проходит со скоростью v = 8 км/ч, а путь S2 (по шоссе) – со скоростью v = 10 км/ч.;
4. Вспомните формулу нахождения пути (расстояния) из курса физики и из этой формулы выразите время ( ). Значит курьер проезжает на велосипеде по полю путь S1 за время t1 =.
). Значит курьер проезжает на велосипеде по полю путь S1 за время t1 =. ; а на велосипеде по шоссе путь S2 за время t2 =
; а на велосипеде по шоссе путь S2 за время t2 = ; Тогда время, затраченное на путь S1 и S2,: t(x) =
; Тогда время, затраченное на путь S1 и S2,: t(x) =  +
+ 
По условию задачи, средствами анализа ищем наименьшие значение функции на отрезке [0;15]. Выполняем решение задачи внутри математической модели, применяя умения решать уравнения, использовать формулы дифференцирования и находить критические точки и наибольшие или наименьшие значение функции на заданном промежутке.
1. Находим производную функции: 
2. Находим критические точки t'(x) = 0; 

25x2 = 16 . (x2 + 81),
9x2 = 16 . 81,
9x2 = 1296,
x2 = 1296 : 9,
x2 = 144,
x1 = 12,
x2 = – 12
Делаем вывод:
точку x2проверять не будем, т.к. она не принадлежит промежутку [0;15].
Находим значение функции в точках x = 0, x = 12, x = 15;
 ;
;
t(15) ~ 2,9;
t(12) ~ 2,18
15 – 12 = 3 км
Критическое осмысление полученного результата, удержание цели занятия и условия задачи позволяет поддерживать высокий уровень активности на протяжении всего занятия. Важным этапом, является интерпретации полученного решения и поиск практического применения.
В какую точку шоссе необходимо ехать, чтобы в кратчайшие время достичь пункта назначения? (Курьеру надо ехать в точку, удаленную на 3 км от населенного пункта и на 12 км от шоссе, чтобы в кратчайшее время достичь населенного пункта.)
Какое практическое значение имеет полученный результат?
Возможно, ли применить полученный опыт использования производной в повседневной жизни, в профессиональной деятельности? (Производная выступает как инструмент изучения интенсивности изменения некоторых экономических объектов (процессов); базовые законы теории производства и потребления, спроса и предложения оказываются прямыми следствиями математических теорем).
Литература:
Н.В.Богомолов, Практические задания по математике: учебное пособие для техникумов, М: Высш.шк.990
А.Н.Колмогороа, А.М.Абрамов и др, Алгебра и начала анализа , учебник для 10-11 классов общеобразовательных учреждений, Москва «Просвещение», 2003
Н.В.Богомолов, П.И.Самойленко Математика, учеб.для ССУЗзов М:Дрофа, 2008







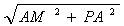 =
=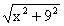 ; S2 = МВ = 15 – х;
; S2 = МВ = 15 – х;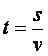 ). Значит курьер проезжает на велосипеде по полю путь S1 за время t1 =.
). Значит курьер проезжает на велосипеде по полю путь S1 за время t1 =.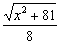 ; а на велосипеде по шоссе путь S2 за время t2 =
; а на велосипеде по шоссе путь S2 за время t2 =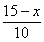 ; Тогда время, затраченное на путь S1 и S2,: t(x) =
; Тогда время, затраченное на путь S1 и S2,: t(x) = 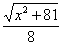 +
+ 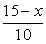
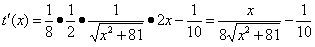
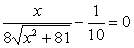
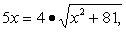 25x2 = 16 . (x2 + 81),
9x2 = 16 . 81,
9x2 = 1296,
x2 = 1296 : 9,
x2 = 144,
x1 = 12,
x2 = – 12
25x2 = 16 . (x2 + 81),
9x2 = 16 . 81,
9x2 = 1296,
x2 = 1296 : 9,
x2 = 144,
x1 = 12,
x2 = – 12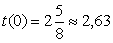 ;
t(15) ~ 2,9;
t(12) ~ 2,18
;
t(15) ~ 2,9;
t(12) ~ 2,18


















