Тела вращения. Конус

Тела вращения. Конус

Прямой круговой конус

Ко́нус — тело, которое состоит из круга – основания конуса, точки, не лежащей в плоскости этого круга, - вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания. Если основание конуса представляет собой многоугольник, конус становится пирамидой.

Примеры тел, имеющих форму конуса:

1. Чум и яранга у северных народов, вигвам у индейцев Северной Америки имеют форму, близкую к форме конуса.

• Отрезок, соединяющий вершину и границу основания, называется образующей конуса.

• Объединение образующих конуса называется образующей (или боковой) поверхностью конуса. Образующая поверхность конуса является конической поверхностью.

• Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса.

• Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания. При этом прямая, соединяющая вершину и центр основания, называется осью конуса.

• Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением.

• Круговой конус — конус, основание которого является кругом.

• Прямой круговой конус (часто его называют просто конусом) можно получить вращением прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось конуса).

• Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом (последние два имеют бесконечный объём).

• Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием, называется усечённым конусом.

• Плоскость, перпендикулярная оси конуса, пересекает конус по кругу, а боковую поверхность – по окружности с центром на оси конуса.

• Сечение конуса плоскостью, параллельной основанию, отсекает от него конус, подобный данному.

• Площадь полной поверхности конуса равна

• Площадь боковой поверхности конуса равна

S = πRl

где R — радиус основания, l — длина образующей.

• Объем кругового конуса равен

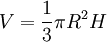
Примеры:

Задача1. Радиус основания конуса 3 м, высота 4 м. Найдите образующую l.

Дано: конус,

r = 3 м,

h =4 м,

Найти: l – образующая конуса

Решение. Рассмотрим прямоугольный треугольник, катетами которого являются высота конуса и радиус основания, а гипотенузой – образующая конуса. По теореме Пифагора получим:

м

Ответ: 5 м.

Задача2. Высота конуса равна 10 см. Найдите площадь сечения, проходящего через вершину конуса и хорду основания, стягивающую дугу в 60°, если плоскость сечения образует с плоскостью основания конуса угол 45°.

Рис. 1.

Решение (см. рис. 1):

Так как хорда АВ основания конуса стягивает дугу в 60° , то она равна радиусу основания: АВ = ОА = ОВ. Проведем  и соединим отрезком точки С и М. Тогда  (по теореме о трех перпендикулярах) и угол МСО — линейный угол двугранного угла с ребром АВ. По условию, МСО = 45°.

В задаче спрашивается площадь сечения, то есть площадь треугольника MAB. .

Найдем сначала OC. Так как треугольник MOC равнобедренный, то OC=OM=10. Тогда гипотенуза .

Рассмотрим ∆COB – прямоугольный, . .

Подставим числа в формулу: .

Ответ: .

Задача 3.Дано: Конус, в основание которого вписан , AC=a, . Образующая конуса наклонена к плоскости основания под углом φ. Найти: Площадь полной поверхности конуса (см. рис. 2).

Рис. 2.

Решение: Чтобы найти площадь поверхности, мы должны знать образующую и радиус основания. По теореме синусов .

Чтобы найти образующую рассмотрим ∆AOP. По условию, угол . Тогда длина образующей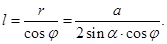

Зная радиус и образующую, подставим их в формулу площади:

Задания

1.Радиус основания конуса R. Осевым сечением конуса является прямоугольный треугольник. Найдите его площадь.

2. В равностороннем конусе (осевое сечение – правильный треугольник) радиус основания R .Найдите площадь сечения, проведенного через две образующие, угол между которыми равен α.

3. Конус пересечен плоскостью, параллельной основанию, на расстоянии d от вершины. Найдите площадь сечения, если радиус основания конуса R, а высота H.

4. Высота конуса H. На каком расстоянии от вершины надо провести плоскость, параллельную основанию, чтобы площадь сечения была равна половине площади основания?

5.Высота конуса равна 15 см, а радиус основания равен 8 см. Найдите образующую конуса.

6. Осевое сечение конуса – прямоугольный треугольник. Найдите площадь этого сечения, если радиус основания конуса равен 5 см.

7. Найдите высоту конуса, если площадь его осевого сечения равна 6 дм², а площадь основания равна 8 дм².

8.Прямоугольный треугольник с катетами 6 см и 8 см вращается вокруг меньшего катета. Вычислите площадь боковой и полной поверхностей образованного при этом вращении конуса.

4