Кто хочет ограничиться настоящим без знания прошлого, тот никогда его не поймет.
Г.В. Лейбниц (немецкий математик XVII-XVIII веков)
1. Из истории квадратных уравнений.
а) Квадратные уравнения в Древнем Вавилоне
Необходимость решать уравнения не только первой, но и второй степени ещё в древности была вызвана потребностью решать задачи, связанные нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н.э. вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения: х2 + х = 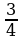 , х2 – х = 14
, х2 – х = 14 
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.
б) Квадратные уравнения в Индии.
Задачи на квадратные уравнения встречаются уже в астрономическом тракте «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабахаттой. Другой индийский ученый, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме: ах2 + bх = с, а 0
В уравнении коэффициенты, кромеа, могут быть отрицательными. Правило Брахмагупта по существу совпадает с нашим.
в) Квадратные уравнения в Европе XIII-XVII вв.
Формулы решения квадратных уравнений по образцу ал-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202 г. Итальянским математиком Леонардо Фибоначчи. Этот объемный труд, в котором отражено влияние математики как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из «Книги абака» переходили почти во все европейские учебники XVI-XVII вв. и частично XVIII.
Общее правило решения квадратных уравнений, приведенных к единому каноническому виду х2 + bх = с, при всевозможных комбинациях знаков коэффициентов b, с было сформулировано в Европе лишь в 1544 г. М.Штифелем.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. Учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
2. Франсуа Виет
Франсуа Виет родился в 1540 году на юге Франции в небольшом городке Фантене-ле-Конт.Отец Виета был прокурором. Сын выбрал профессию отца и стал юристом, окончив университет в Пуату. В 1560 году двадцатилетний адвокат начал свою карьеру в родном городе, но через три года перешел на службу в знатную гугенотскую семью де Партене. Он стал секретарем хозяина дома и учителем его дочери двенадцатилетней Екатерины. Именно преподавание пробудило в молодом юристе интерес к математике.
Когда ученица выросла и вышла замуж, Виет не расстался с ее семьей и переехал с нею в Париж, где ему было легче узнать о достижениях ведущих математиков Европы. Он общался с видным профессором Сорбонны Рамусом, с крупнейшим математиком Италии Рафаэлем Бомбелли вел дружескую переписку.
В 1571 году Виет перешел на государственную службу, став советником парламента, а затем советником короля Франции Генриха III.
В 1580 году Генрих III назначил Виета на важный государственный пост рекетмейстера, который давал право контролировать выполнение распоряжений в стране и приостанавливать приказы крупных феодалов.
В 1584 году по настоянию Гизов Виета отстранили от должности и выслали из Парижа. Обретя покой и отдых, ученый поставил своей целью создание всеобъемлющей математики, позволяющей решать любые задачи.
Виет изложил программу своих исследований и перечислил трактаты, объединенные общим замыслом и написанные на математическом языке новой буквенной алгебры, в изданном в 1591 году знаменитом "Введение в аналитическое искусство". Основу своего подхода Виет называл видовой логистикой, он четко разграничивал числа, величины и отношения, собрав их в некую систему "видов". В эту систему входили, например, переменные, их корни, квадраты, кубы, квадрато-квадраты и т. д. Для этих видов Виет дал специальную символику, обозначив их прописными буквами латинского алфавита. Для неизвестных величин применялись гласные буквы, для переменных - согласные.
Виет показал, что, оперируя с символами, можно получить результат, который применим к любым соответствующим величинам, т. е. решить задачу в общем виде. Это положило начало коренному перелому в развитии алгебры: стало возможным буквенное исчисление.
Знаменитая теорема, устанавливающая связь коэффициентов многочлена с его корнями, была обнародована в 1591 году. Теперь она носит имя Виета, а сам автор формулировал ее так: "Если В+D, умноженное на А, минус А в квадрате равно ВD, то А равно В и равно D".
В трактате "Дополнения к геометрии" он стремился создать некую геометрическую алгебру, используя геометрические методы для решения уравнений третьей и четвертой степеней. Любое уравнение третьей и четвертой степени, утверждал Виет, можно решить геометрическим методом трисекции угла или построением двух средних пропорциональных.
Виет первым явно сформулировал в словесной форме теорему косинусов, хотя положения, эквивалентные ей, эпизодически применялись с первого века до нашей эры. Известный ранее своей трудностью случай решения треугольника по двум данным сторонам и одному из противолежащих им углов получил у Виета исчерпывающий разбор. Глубокое знание алгебры давало Виету большие преимущества. Причем интерес его к алгебре первоначально был вызван приложениями к тригонометрии и астрономии. Не только каждое новое применение алгебры давало импульс новым исследованиям по тригонометрии, но и полученные тригонометрические результаты являлись источником важных успехов алгебры. Виету, в частности, принадлежит вывод выражений для синусов (или хорд) и косинусов кратных дуг.
В мемуарах некоторых придворных Франции есть указание, что Виет был женат, что у него была дочь, единственная наследница имения, по которому Виет звался Сеньор ДеЛаБиготье. В придворных новостях маркиз Летуаль писал: «14 февраля 1603 г. господин Виет, рекетмейстер, человек большого ума и рассуждения и один из самых ученых математиков века умер в Париже. Ему было более шестидесяти лет».
Определение квадратного уравнения и их виды.
Квадратным уравнением называют уравнение вида ах²+bх+с=0, где коэффициенты, а, b, с - любые действительные числа, причем, а≠0. Коэффициенты, а, b, с, различают по названиям: а – первый или старший коэффициент; b – второй или коэффициент при х; с – свободный член, свободен от переменной х.
Квадратное уравнение также называют уравнением второй степени, так как его левая часть есть многочлен второй степени.
Квадратное уравнение называют приведенным, если старший коэффициент равен 1; квадратное уравнение называют неприведенным, если старший коэффициент отличен от 1.
х²+рх+q=0 – стандартный вид приведенного квадратного уравнения
Кроме приведенных и неприведенных квадратных уравнений различают также полные и неполные уравнения.
Полное квадратное уравнение – это квадратное уравнение, в котором присутствуют все три слагаемых; иными словами, это уравнение, у которого коэффициенты b и с отличны от нуля.
Неполное квадратное уравнение – это уравнение, в котором присутствуют не все три слагаемых; иными словами, это уравнение, у которого хотя бы один из коэффициентов b и с равен нулю.
Квадратное уравнение

Полное Неполное


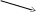

Приведенное а=1 если b=0 если с=0
Неприведенное а≠1 если b=0, c=0
Корнем квадратного уравнения ах²+bх+с=0 называют всякое значение переменной х, при котором квадратный трехчлен ах²+bх+с обращается в нуль.
Можно сказать, и так: корень квадратного уравнения – это такое значение х, подстановка которого в уравнение обращает уравнение в верное числовое равенство (0=0).
Решить квадратное уравнение – найти все его корни или установить, что их нет.
Решение неполных квадратных уравнений
Сначала математики научились решать неполные квадратные уравнения, поскольку для этого не пришлось, как говорится, ничего изобретать.
| Если b=0, то ах²+ с=0 | Если с=0, то ах²+bх=0 | Если b=0, с=0, то ах²=0 |
| ах²+ с=0, ах²= -с, х² = -с/а, Если 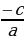 ≥ 0, то уравнение имеет ≥ 0, то уравнение имеет 2 корня х=±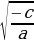 Если 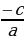 не имеет. | ах²+bх=0, х(ах+b)=0, х=0 или ах+b=0; х=0 или х=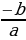 . . | ах²=0, х²=0, х=0. |
Неполное квадратное уравнение может иметь два корня, один корень и ни одного корня.
Пример: х2+18х=0
Общий множитель x выносим за скобки: х(х+18)=0
Это уравнение типа «произведение равно нулю». Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:
х=0; х+18=0
х=0; х=-18
Ответ: 0; -18.
Пример: 7х2-28=0
7х2=28 (:7)
х2=4
х=±2
Ответ:±2.
Пример:2х2+8=0
2х2=-8
х2=-4
Корней нет, так как квадратный корень не может равняться отрицательному числу.
Ответ: нет корней.
Решение квадратных уравнений по формуле.
Рассмотрим уравнение вида: ах2+bх+с=0, а ≠ 0.
Умножим обе части уравнения ах2+bх+с=0, на 4а и последовательно имеем:
4а2х2 + 4аbх + 4ас = 0,((2ах)2 + 2ах∙b + b2) - b2 + 4ac = 0,
(2ax + b)2 = b2 - 4ac,
2ax + b = ± √ b2 - 4ac,2ax = - b ± √ b2 - 4ac,
Корни уравнения ах2 + bх + с = 0, а ≠ 0 можно найти по формуле
 , где выражение b2 - 4ac= D называется дискриминантом.
, где выражение b2 - 4ac= D называется дискриминантом.
Таким образом:
1. В случае положительного дискриминанта, т.е. при b2 - 4ac0,
то уравнение ах2 + bх + с = 0 имеет два различных корня.
2. Если дискриминант равен нулю, т.е. b2 - 4ac = 0, то уравнение ах2 + bх + с = 0 имеет один корень x=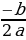 .
.
3.Если дискриминант отрицателен, т.е. b2 - 4ac2 + bх + с = 0 не имеет корней.
Пример 1:3х2+4х-7=0
а=3, b=4, с= -7,
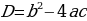 ,
,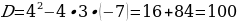 ,
,
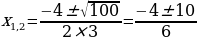 ,
,
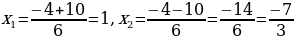 .
.
Ответ: х1 =1, х2=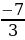 ,
,
| Пример 2:4х2 - 4х + 1 = 0, а = 4, b = - 4, с = 1, D = b2 - 4ac, D = (-4)2 - 4 ∙ 4 ∙ 1= 16 - 16 = 0, D = 0, один корень; х= 4/8=1/2=0,5 Ответ: х=0,5
| Пример 3:2х2 + 3х + 4 = 0, а = 2, b = 3, с = 4, D = b2 - 4ac = 32 - 4 ∙ 2 ∙ 4 = 9 - 32 = - 13, D Данное уравнение корней не имеет. Ответ: нет корней.
|
Вывод: Плюс: Можно применить ко всем квадратным уравнениям.
Минус: Нужно выучить формулы.
Решение квадратных уравнений выделением полного квадрата двучлена.
Рассмотрим уравнение вида: 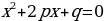 ,
,
 ,
,
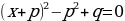 ,
,
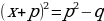 ,
,
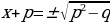 ,если
,если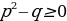 ,
,
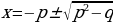 ,
,
Пример 1: х2 + 6х - 7 = 0.
Выделим в левой части полный квадрат. Для этого запишем уравнение в виде: х2 + 2 ∙ х ∙ 3 + 32 - 32 - 7 =0, (х + 3)2 - 9 - 7 =0, (х + 3)2 – 16=0. Таким образом, данное уравнение можно записать так: (х + 3)2 = 16. Следовательно, х + 3 = -4, х1 = -7, или х + 3 = 4, х1 = 1.
Ответ: х1 = -7, х2 = 1.
Пример 2: 3х2+4х-7=0,
 ,
,
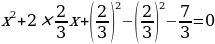 ,
,
��
 ,
,
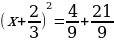 ,
,
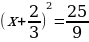 ,
,
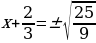 ,
,
��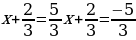
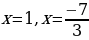 .
.
Ответ: х1=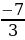 , х2 =1
, х2 =1
Вывод:
Плюс: За минимальное количество действий можно найти корни уравнений.
Минус: Нужно правильно найти все слагаемые для выделения полного квадрата. Сложность выделения полного квадрата при дробных коэффициентах.
Решение квадратных уравнений разложением на множители.
При решении квадратных уравнений часто применяется метод разложения на множители (с помощью вынесения за скобки общего множителя, формул сокращенного умножения или способа группировки).
Пример 1: х2 + 10х - 24 = 0.
Разложим левую часть на множители: х2+12х-2х-24 =0, х(х+12)-2(х+12)=0.
Следовательно, уравнение можно переписать так: (х+12)(х-2)=0.
Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х1 =-12, х2 =2. Это означает, что число 2 и -12 являются корнями уравнения х2 + 10х - 24 = 0.
Ответ: х1=-12, х2 =2.
Пример 2: 3х2+4х-7=0
Разложим левую часть на множители: 3х2+7х -3х -7=0, х(3х+7)-(3х+7)=0.
Следовательно, уравнение можно переписать так: (3х+7)(х-1)=0
Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается в нуль при х1= 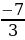 , х2 =1. Это означает, что число
, х2 =1. Это означает, что число 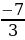 и1 являются корнями уравнения3х2+4х -7=0.
и1 являются корнями уравнения3х2+4х -7=0.
Ответ: х1=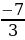 , х2 =1.
, х2 =1.
Вывод:
Плюс: Дает возможность сразу увидеть корни уравнения.
Минус: Нужно правильно вычислить слагаемых для группировки.
Решение квадратных уравнений при помощи теоремы Виета.
Для решения полного квадратного уравнения ах2+bх+с=0 по теореме Виета нужно разделить всё уравнение на коэффициент а.
Для уравнения 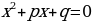 , если
, если 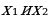 его корни, справедливы формулы:
его корни, справедливы формулы:
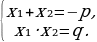
Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).
а) Если сводный член q приведенного уравнения положителен (q 0), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p. Если р 0, то оба корня отрицательны, если р , то оба корня положительны.
Например,
x2 – 3x + 2 = 0; x1 = 2 и x2 = 1, так как q = 2 0 и p = - 3
x2 + 8x + 7 = 0; x1 = - 7 и x2 = - 1, так как q = 7 0 и p= 8 0
Пример 1:х2-9х+14=0
Решение. Имеем 14=1∙14=2∙7 и 2+7=9. Значит, х1= 2, х2 =7.
Ответ: х1= 2, х2 =7.
б) Если свободный член q приведенного уравнения отрицателен (q ), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p , или отрицателен, если p 0.
Например,
x2 + 4x – 5 = 0; x1 = - 5 и x2 = 1, так как q= - 5 и p = 4 0;
x2 – 8x – 9 = 0; x1 = 9 и x2 = - 1, так как q = - 9 и p = - 8
Пример 1. х2-2х-15=0.
Из всех множителей числа 15 (1 и 15, 3 и 5) выбираем те, разность которых равна 2. Это числа 3 и 5. Перед меньшим числом ставим второй знак уравнения, т.е. «минус». Таким образом, х1=-3, х2=5,-корни уравнения.
ПРИМЕР 2: х2+10х-24=0
Решение. Так как 24=1∙24=2∙12=3∙8=4∙6 и 10=12-2, х1=2, х2=-12
Ответ: х1=2, х2=-12.
ПРИМЕР 3: х2 –4х-77=0.
Решение. Имеем 77=7∙11и 11-7=4, х1=-7, х2=11.
Ответ: х1=2, х2=-12.
в) Если в уравнении второй коэффициент p и сводный член q приведенного уравнения положительны(p 0 и q 0), то оба корня отрицательны. Чтобы найти корни, нужно найти такие множители свободного члена, чтобы их сумма была равна р.
ПРИМЕР: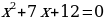
Решение. Так как 12=1∙12=2∙6=3∙4 и3+4=7, а в уравнении два «плюса» то ответом является х1= -3, х2 =-4.
Ответ: х1= -3, х2 =-4.
Неприведенные квадратные уравнения
Решение уравнений вида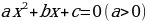 , практически незнакомо учащимся, хотя алгоритм решения немногим отличается от алгоритма решения приведенного квадратного уравнения. Для того, чтобы пользоваться алгоритмом, условимся рассматривать уравнения с положительным коэффициентом а.Корни уравнения имеют вид
, практически незнакомо учащимся, хотя алгоритм решения немногим отличается от алгоритма решения приведенного квадратного уравнения. Для того, чтобы пользоваться алгоритмом, условимся рассматривать уравнения с положительным коэффициентом а.Корни уравнения имеют вид 
ПРИМЕР 1. 5х2+12х+4=0
Решение. Найдем числа, произведение которых равно 4∙5=20, а сумма 12. Это числа 2 и 10.Поскольку в уравнении два «плюса», искомые числители дробей отрицательны: -2 и -10. Знаменателем дробей является первый коэффициент 5. Итак, 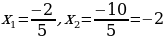
Ответ: х1= -2/5, х2 =-2.
ПРИМЕР 2. 7х2-4х-11=0
Решение. Найдем числа, произведение которых равно7∙11=77, а разность равна 4. Это числа 7 и 11. Меньшее из них должно иметь знак «минус», т.е искомые числители дробей равны -7 и 11, а в знаменателе первый коэффициент 7. Таким образом, 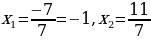
Ответ: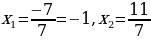
ПРИМЕР 3. Решить уравнение 
Решение. Зачем, что 67+8=75, следовательно, .
.
Ответ: х1= 1, х2 =8/67.
ПРИМЕР 4. Решить уравнение 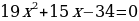
Решение. Так как34-19=15, то искомые числители дробей равны 19 и -34, тогда
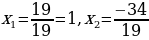
Ответ: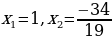
Таким образом, к любому приведенному квадратному уравнению 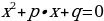 можно применить следующий алгоритм отыскания корней:
можно применить следующий алгоритм отыскания корней:
Найти множители свободного члена, для которых действие, указанное последним знаком уравнения, дает второй коэффициент;
Расставить знаки у найденных множителей по следующим правилам
-если последний знак «минус», то меньшему корню присваивается второй знак уравнения (больший корень имеет противоположный знак).
-если в уравнении два «плюса», то в ответе два «минуса».
ПРИМЕР 1. Решить уравнение 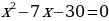
Решение. Среди множителей числа 30 ищем такие, разность которых равна 7. Это числа 3 и 10. Меньшему числу присваиваем знак «минус»; Таким образом, 
Ответ: х1= 3, х2 =10.
ПРИМЕР 2. Решить уравнение 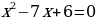
Решение. Среди множителей числа 6 ищем такие, сумма которых равна 7. Это числа 1 и 6. Таким образом, х1= 1, х2 =6.
Ответ: х1= 1, х2 =6.
ПРИМЕР 3. Решить уравнение 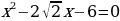
Решение. Имеем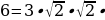 ,a
,a
ПРИМЕР 4. Решить уравнение 
Решение. Поскольку 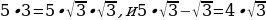 , находим
, находим 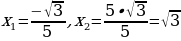
Вывод:
Плюс: Достаточно легкий способ, дает возможность сразу увидеть корни уравнения, экономит время.
Минус: легко находятся только целые корни, не целые коэффициенты b и с.
Решение квадратных уравнений с помощью свойств коэффициентов.
1.Прием переброски старшего коэффициента.
Рассмотрим квадратное уравнение ах2+bх+с =0, где а ≠0.
Умножая обе его части на а, получаем уравнение а2х2 +аbх+ас=0.
Пусть ах = у, откуда х = у/а; тогда приходим к уравнению у2 + by + ас = 0, равносильно данному. Его корни у1 и у2 найдем с помощью теоремы Виета. Окончательно получаем х1 = у1/а и х2 = у2/а. При этом способе коэффициента умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Пример: 2х2 – 11х + 15 = 0.
Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение у2 – 11у + 30 = 0.
Согласно теореме Виета
у1 = =5 х1 = 5/2 x1 = 2,5
у2 = 6 x2 = 6/2 x2 = 3.
Ответ: х1 =2,5; х2=3.
2. Сумма коэффициентов квадратного уравнения: ах2+вх+с=0:
а) Если выполняется условиеа+в+с=0, то х1=1, х2=.
Пример: 21х2-3940х+3919=0.
Решение. Так как 21-3940+3919=0 то, х1=1, х2= 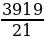
Пример: 345х2 – 137х – 208 = 0.
Решение. Так как345 – 137 – 208 = 0, то х1 = 1, х2 = c/a = -208/345.
Ответ: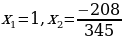
Пример:132х2 – 247х + 115 = 0.
Решение. Так как 132 – 247 + 115 = 0, то х1 = 1, х2 = c/a = 115/132.
Ответ: .
.
б) Если а-в+с=0, то х1=-1, х2=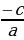 .
.
Пример: х2+1357х+1356=0.
Решение. Так как 1-1357+1356=0, то х1=-1, х2=-1356.
3. Метод решения квадратных уравнений вида: ах2± (а2+1)х ± а=0.
а) В уравнениях вида ах2+(а2+1)х+а=0 корни х1=- а, х2=-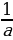 .
.
Пример: 25х2+626х+25=0, х1=- 25, х2= - – .
.
б) В уравнениях вида ах2- (а2+1)х+а=0 корни х1= а, х2=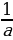 .
.
Пример: 13х2- 170х+13=0, х1=13, х2=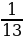 .
.
в) В уравнениях вида ах2+(а2+1)х- а=0 корни х1=- а, х2=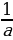 .
.
Пример: 25х2+626х – 25=0, х1=- 25, х2=  .
.
г) В уравнениях вида ах2- (а2+1)х- а=0 корни х1= а, х2= -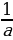 .
.
Пример: 13х2- 170х-13=0, х1=13, х2=-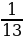 .
.
4. Решение квадратных уравнений по формуле с четным коэффициентом.
Если второй коэффициент уравненияb =2k– четное число, то формулу корней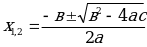 можно записать в виде
можно записать в виде 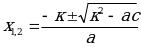
Приведенное уравнение х2 + рх + q= 0 совпадает с уравнением общего вида, в котором а = 1, b = р и с = q. Поэтому для приведенного квадратного уравнения формула корней принимает вид
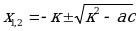
Формулу удобно использовать, когда р— четное число.
Пример: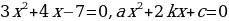 ,
,
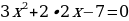 ,
,
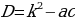 ,
,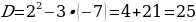 ,
,
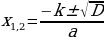 ,
, 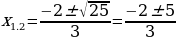 ,
,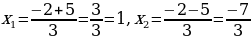 .
.
Ответ: х1 =1, х2=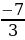 ,
,
Пример:3х2 — 14х + 16 = 0.
Решение. Имеем: а = 3, b = — 14, с = 16, k = — 7;
D = k2 – ac = (- 7)2 – 3 • 16 = 49 – 48 = 1, D 0, два различных корня;
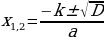 ,
, 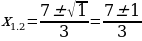 ,
,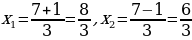 =2
=2
Ответ: х2=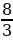 , х2 =2.
, х2 =2.
Вывод: Плюс: За минимальное количество действий можно найти корни уравнения, применяется совместно со способом теоремы Виета.
Минус: легко найти только целые корни.
Графическое решение квадратных уравнений.
| Если в уравнении х2+px+q= 0 перенести второй и третий члены в правую часть, то получим уравнение х2= - px - q. Построим в одной системе координат графики зависимости у = х2 и у = - px - q. График первой зависимости - парабола, проходящая через начало координат. График второй зависимости -прямая Возможны следующие случаи: 1) прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения; 2) прямая и парабола могут касаться (только одна общая точка), т.е. уравнение имеет одно решение; 3) прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней. | 
|
| Пример:х2 - 3х - 4 = 0 Запишем уравнение в виде х2 = 3х + 4. Построим параболу у = х2 и прямую у = 3х + 4. Прямую у = 3х + 4 построим по двум точкам М (0; 4) и N (3; 13). Прямая и парабола пересекаются в двух точках А и В с абсциссами х1 = - 1 и х2 = 4. Ответ: х1 = - 1; х2 = 4. | 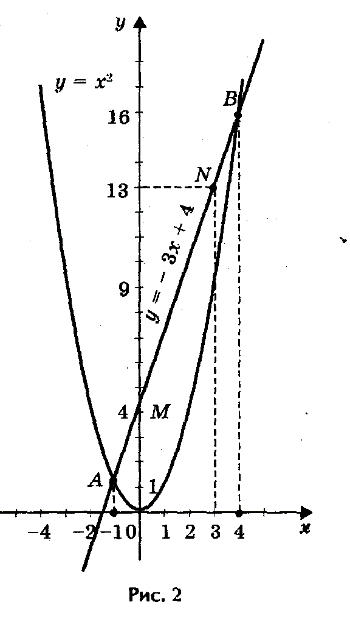
|
| Пример:х2 - 2х + 1 = 0. Решение. Запишем уравнение в виде х2 = 2х - 1. Построим параболу у = х2и прямую у = 2х - 1. Прямую у = 2х - 1 построим по двум точкам М (0; - 1) и N (1/2; 0). Прямая и парабола пересекаются в точке А с абсциссой х = 1. Ответ: х = 1. | 
|
| Пример:х2 - 2х + 5 = 0. Решение. Запишем уравнение в виде х2 = 5х - 5. Построим параболу у = х2 и прямую у = 2х - 5. Прямую у = 2х - 5 построим по двум точкам М(0; - 5) и N(2,5; 0). Прямая и парабола не имеют точек пересечения, т.е. данное уравнение корней не имеет. Ответ: корней нет. | 
|
Вывод: Плюс: Наглядный способ.
Минус: Применяя графический метод, не всегда можно найти точное значение корней. Поэтому этот метод часто применяют не для нахождения корней уравнения, а для определения их количества.
Решение квадратных уравнений с помощью циркуля и линейки
Решим уравнение ах2+bх+с = 0 с помощью циркуля и линейки.
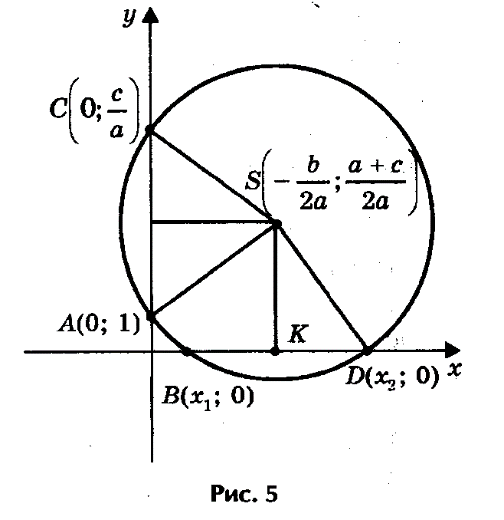
Допустим, что искомая окружность пересекает ось абсцисс в точках В (х1;0) и D (х2;0), где х1 и х2 - корни уравнения ах2 +bх+с=0, и проходит через точки А(0;1) и С(0;c/a) на оси ординат. Тогда по теореме о секущих имеем OB∙OD = OA∙OC, откуда OC = OB∙OD/ OA= х1х2/ 1 = c/a.
 Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, поэтому
Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, поэтому
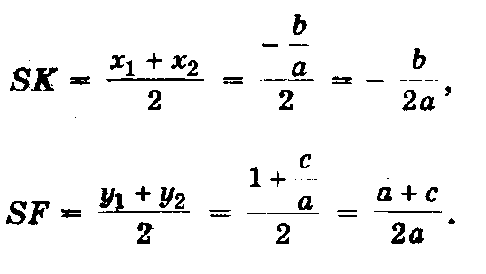
И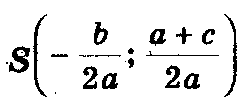 так:
так:
1) построим точки (центр окружности) и A(0; 1);
2) проведем окружность с радиусом SA;
3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.
При этом возможны три случая.
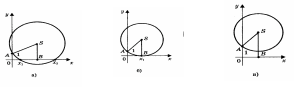
1) Радиус окружности больше ординаты центра (ASSK, или R(a + c)/2a), окружность пересекает ось Ох (рис.а) в двух точках В(х1; 0) и D(х2; 0), где х1 и х2 - корни квадратного уравнения ах2 + bх + с = 0.
2) Радиус окружности равен ординате центра (AS = SB, или R=(a + c)/2a), окружность касается оси Ох (рис.б) в точке В(х1; 0), где х1 - корень квадратного уравнения.
3) Радиус окружности меньше ординаты центра (ASSB, или R
окружность не имеет общих точек с осью абсцисс (рис в), в этом случае уравнение не имеет решения.
| Пример: 3х2 + 4х - 7 = 0 Решение. Определим координаты точки центра окружности по формулам: 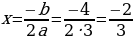 , , . .
Проведем окружность радиуса SA, где А (0; 1).  . .
Ответ: х1= -7/3; х2=1. | 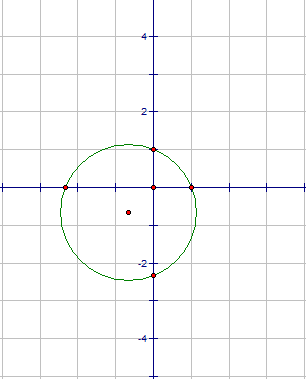
|
| Пример: х2 - 2х - 3 = 0 Решение. Определим координаты точки центра окружности по формулам:  , ,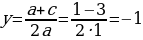
Проведем окружность радиуса SA, где А (0; 1).х1 = - 1; х2 = 3 Ответ:х1 = - 1; х2 = 3. | 
|
| Пример: х2+4х+4=0 Решение. Определим координаты точки центра окружности по формулам: 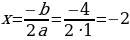 , ,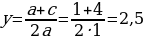
Проведем окружность радиуса SA, где А (0; 1).х1 = - 2 Ответ:-2 | 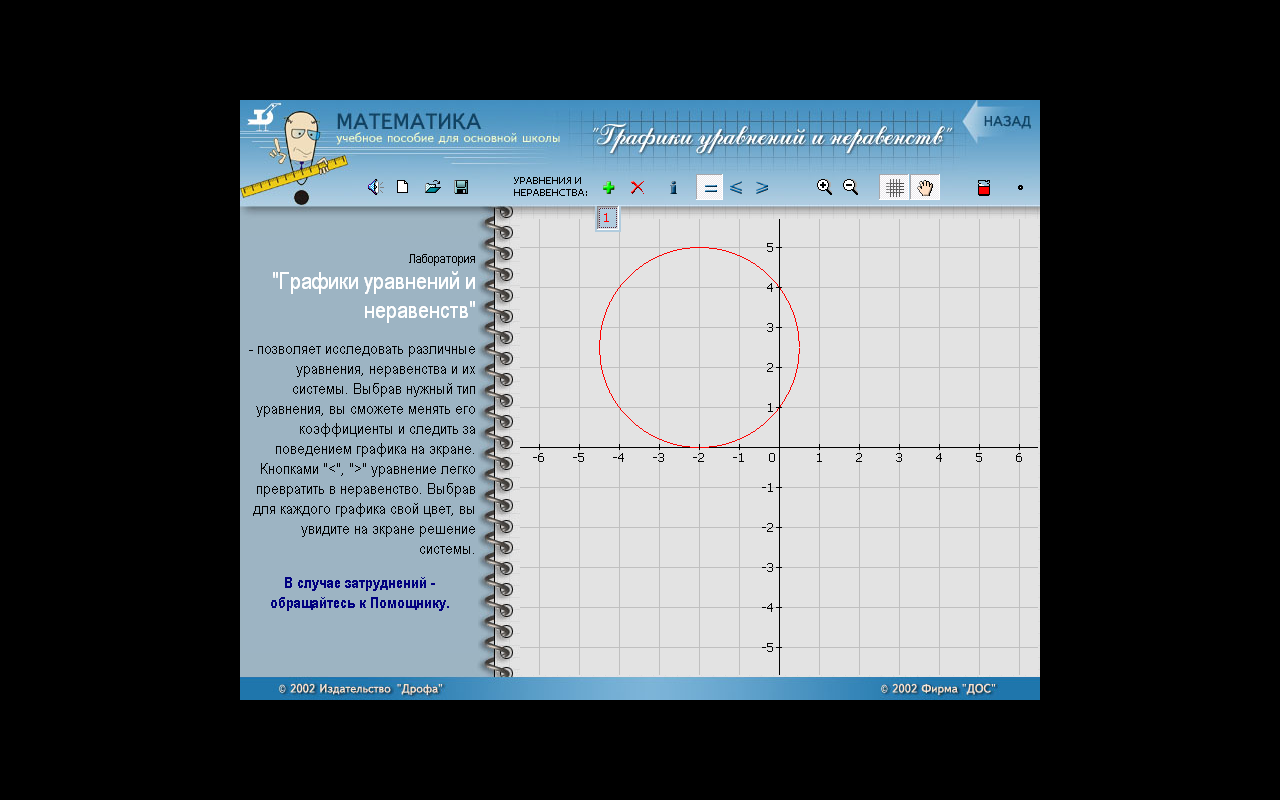
|
| Пример: х2-2х+3=0 Решение. Определим координаты точки центра окружности по формулам:  , ,

Проведем окружность радиуса SA, где А (0; 1). Ответ: нет корней. | 
|
Вывод:
Плюс: Наглядный способ.
Минус: Могут быть не точности
Решение квадратных уравнений с помощью номограммы.
Номограмма (от греческого «nomos» – закон и грамма), графическое представление функции от нескольких переменных, позволяющее с помощью простых геометрических операций (например, прикладывание линейки) исследовать функциональные зависимости без вычислений. Например, решать квадратное уравнение без применения формул.
Это старый и незаслуженно забытый способ решения квадратных уравнений, помещенный на с.83 (Брадис В.М. Четырехзначные математические таблицы. – М., Просвещение, 1990).
Номограмма для решения уравнения х2 + pх + q = 0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.
| Пример:х2 –9х + 8 = 0. p = -9, q = 8 Номограмма дает корни х1 = 8 их2 = 1.
| 
|
| Пример:2х2 –9х +2 = 0. Разделим коэффициенты этогоуравнения на 2, получим уравнение х2– 4, 5х+1 =0. p = -4,5, q = 1 Номограмма дает корни х1 = 4 и х2 = 0,5. |
| Пример:х2 + 5х –6 =0 p = 5, q = -6 номограмма даетположительный корень х1 = 1, а отрицательныйкорень находим, вычитая положительный корень из –р, т.е.х2 = – р – х1 = –5 –1 = –6 | 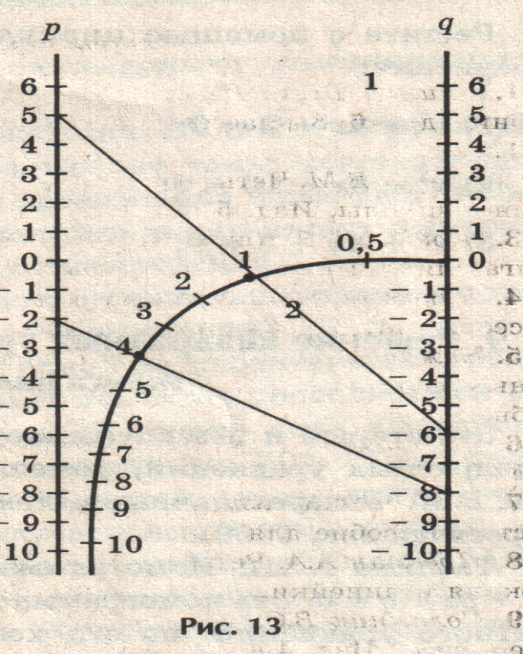
|
| Пример: х2 – 2х – 8 = 0 p = -2, q = -8 номограмма даетположительныйкорень х1 = 4, а отрицательныйравенх2 = – р –х1 =2 – 4 = –2. |
Вывод:
Плюс: Наглядный способ.
Минус: Могут быть не точности
Геометрический способ решения квадратных уравнений
В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведем ставший знаменитым пример из «Алгебры» ал - Хорезми.
| Пример:х2 + 10х = 39.В оригинале эта задача формулируется следующим образом: «Квадрат и десять корней равны 39». Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата, сторона каждого из них 2,5, а площадь 6,25. Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х2, четырех прямоугольников (42,5х = 10х ) и четырех пристроенных квадратов (6,25 4 = 25), т.е. S =х2 + 10х + 25. Заменяя х2 + 10х числом 39, получим, что S = 39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т.е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим х+5=±8, 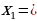 -13, -13, 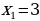 | 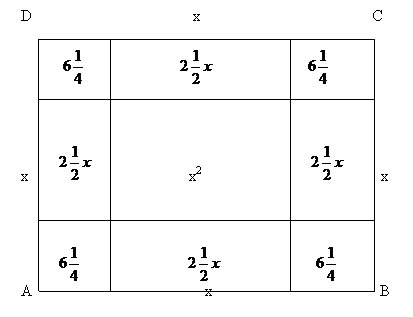
|
| Пример: как древние греки решали уравнение у2 + 6у - 16 = 0. Решение: у2 + 6у = 16, или у2 + 6у + 9 = 16 + 9. Выражения у2 + 6у + 9 и 16 + 9 геометрически представляют собой один и тот же квадрат, а исходное уравнение у2 + 6у - 16 + 9 - 9 = 0 - одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у1 = 2, у2 = - 8. | 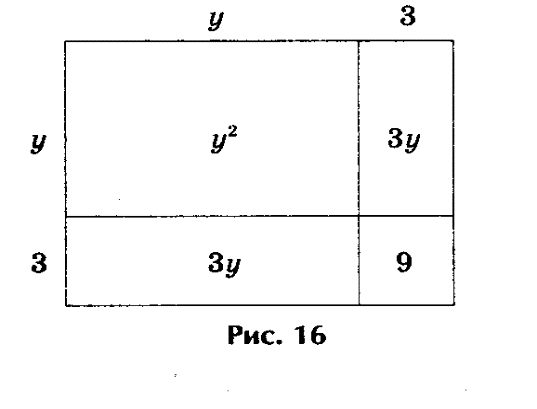
|
| Пример: у2 - 6у - 16 = 0. Преобразуя уравнение, получаем у2 - 6у = 16. На рисунке находим «изображения» выражения у2 - 6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3. Значит, если к выражению у2 - 6у прибавить 9, то получим площадь квадрата со стороной у - 3. Заменяя выражение у2 - 6у равным ему числом 16, получаем: (у - 3)2 = 16 + 9, т.е. у - 3 = ± √25, или у - 3 = ± 5, где у1 = 8 и у2 = - 2. | 
|
Вывод:
Плюс:Наглядный способ.
Минус:похож на способ выделения полного квадрата.
Геометрический способ использовался в древности, когда не было известно алгебраических способов решения. В современной жизни не находит применения.
Сравнение различных способов решения квадратных уравнений
| Метод | Плюсы | Минусы |
| Формула корней квадратного уравнения с использованием дискриминанта | Универсальность, т.к. можно использовать для решения абсолютно всех квадратных уравнений | Громоздкий дискриминант, не входящий в таблицу квадратов |
| Теорема Виета | Быстрота решения в определённых случаях и экономия времени | Если дискриминант не является полным квадратом целого числа. Не целые коэффициенты b и с. |
| Выделение полного квадрата | При правильном преобразовании в квадрат двучлена получаем квадратное уравнение неполного вида и следовательно быстрее находятся корни | Сложность выделения полного квадрата при дробных коэффициентах уравнения |
| Способ группировки | Можно решить, не зная формул | Не всегда среднее слагаемое удаётся разложить на подходящие слагаемые для группировки |
| Графический способ | Не требуется формул. Можно быстро узнать количество корней уравнения | Приближённость решения |
| Свойства коэффициентов a,b,c | Быстрота решения. Для уравнений с большими коэффициентами | Подходит только для некоторых уравнений |
| «Переброс» главного коэффициента | Быстрота решения, если корни целые | Такие же как с помощью теоремы Виета |
| Номограмма | Наглядность Все, что требуется для решения–это номограмма | Не всегда имеется с собой номограмма. Неточность решения |
| Нахождение корней с помощью циркуля и линейки | Наглядность | Если координаты центра нецелые числа. Нахождении корней уравнений с большими коэффициентами |






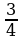 , х2 – х = 14
, х2 – х = 14 




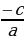 ≥ 0, то уравнение имеет
≥ 0, то уравнение имеет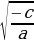
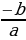 .
. , где выражение b2 - 4ac= D называется дискриминантом.
, где выражение b2 - 4ac= D называется дискриминантом.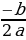 .
.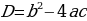 ,
,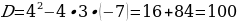 ,
,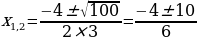 ,
,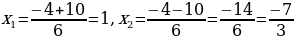 .
.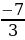 ,
,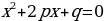 ,
, ,
,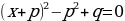 ,
,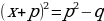 ,
,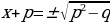 ,если
,если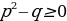 ,
,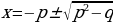 ,
, ,
,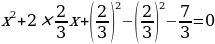 ,
,
 ,
,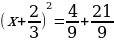 ,
,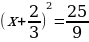 ,
,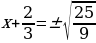 ,
,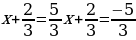
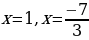 .
.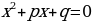 , если
, если 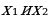 его корни, справедливы формулы:
его корни, справедливы формулы: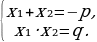
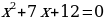
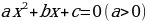 , практически незнакомо учащимся, хотя алгоритм решения немногим отличается от алгоритма решения приведенного квадратного уравнения. Для того, чтобы пользоваться алгоритмом, условимся рассматривать уравнения с положительным коэффициентом а.Корни уравнения имеют вид
, практически незнакомо учащимся, хотя алгоритм решения немногим отличается от алгоритма решения приведенного квадратного уравнения. Для того, чтобы пользоваться алгоритмом, условимся рассматривать уравнения с положительным коэффициентом а.Корни уравнения имеют вид 
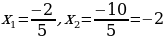
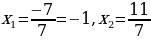

 .
.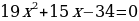
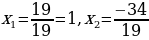
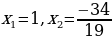
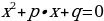 можно применить следующий алгоритм отыскания корней:
можно применить следующий алгоритм отыскания корней: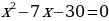

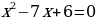
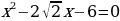
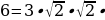 ,a
,a

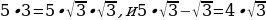 , находим
, находим 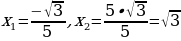

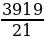
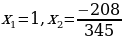
 .
.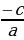 .
. 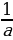 .
.  .
.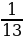 .
.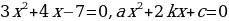 ,
,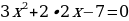 ,
,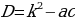 ,
,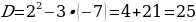 ,
,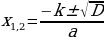 ,
, 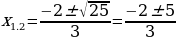 ,
,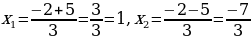 .
.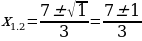 ,
,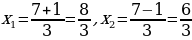 =2
=2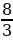 , х2 =2.
, х2 =2.



 Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, поэтому
Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, поэтому
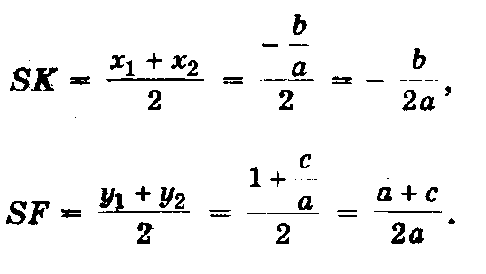

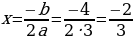 ,
, .
. .
.
 ,
,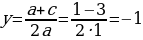

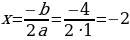 ,
,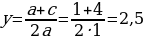





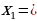 -13,
-13,