Презентация по теме "Четырехугольники" (геометрия 8 класс)

Четырехугольники

Четырехугольники

Невыпуклые

Выпуклые

Трапеция

Параллелограмм

Ромб

Прямоугольник

Квадрат

Четырехугольники

C

ABCD – четырехугольник

A , B , C , D – вершины

A и B , C и D – соседние вершины (вершины четырехугольника, являющиеся концами одной из его сторон)

A и C , B и D – противолежащие вершины (вершины, не являющиеся соседними)

AC и BD – диагонали (Отрезки, соединяющие противолежащие вершины четырехугольника)

B

D

A

C

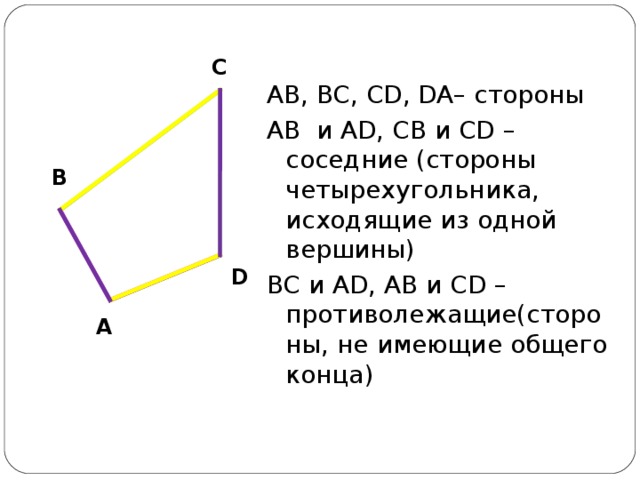
AB, BC, CD, DA – стороны

AB и AD, CB и CD – соседние (стороны четырехугольника, исходящие из одной вершины)

BC и AD, AB и CD – противолежащие(стороны, не имеющие общего конца)

B

D

A

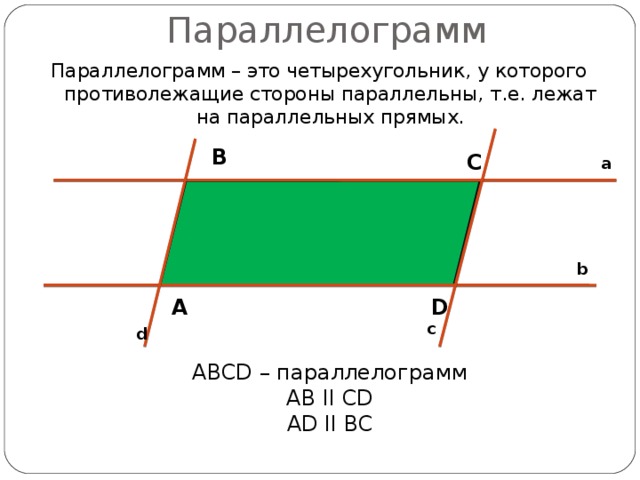
Параллелограмм

Параллелограмм – это четырехугольник, у которого противолежащие стороны параллельны, т.е. лежат на параллельных прямых.

B

C

а

b

A

D

c

d

ABCD – параллелограмм

AB II CD

AD II BC

∟ABO=∟COD (Внутренние накрестлежащие при прямых AB и CD и секущей BD ) = AB II CD D A 2) Аналогично доказывается, что ∆ BOC = ∆ DOA = ∟BCO=∟DAO (внутренние накрестлежащие при прямых BO и AD и секущей AC) = BC II AD 3 ) AB II CD BC II AD = ABCD является параллелограммом. Ч.т.д. " width="640"

Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.

C

B

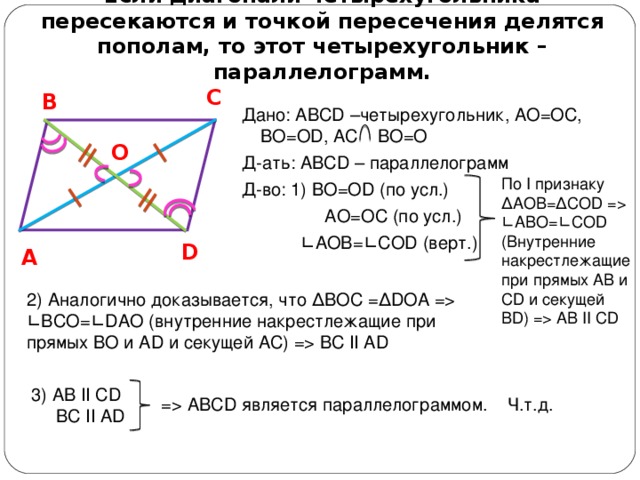
Дано: ABCD –четырехугольник, AO=OC, BO=OD, AC BO=O

Д-ать: ABCD – параллелограмм

Д-во: 1) BO=OD (по усл.)

AO=OC (по усл.)

∟ AOB=∟COD (верт.)

O

По I признаку ∆ AOB = ∆COD = ∟ABO=∟COD (Внутренние накрестлежащие при прямых AB и CD и секущей BD ) = AB II CD

D

A

2) Аналогично доказывается, что ∆ BOC = ∆ DOA = ∟BCO=∟DAO (внутренние накрестлежащие при прямых BO и AD и секущей AC) = BC II AD

3 ) AB II CD

BC II AD

= ABCD является параллелограммом. Ч.т.д.

ABC 1 D - параллелограмм = BC 1 II AD D A = противоречие ( через т. B проходят 2 прямые параллельные AD ) = AC BD=O AO=OC, BO=OD Ч.т.д. AC 1 II AD BD II AD ( по усл.) " width="640"

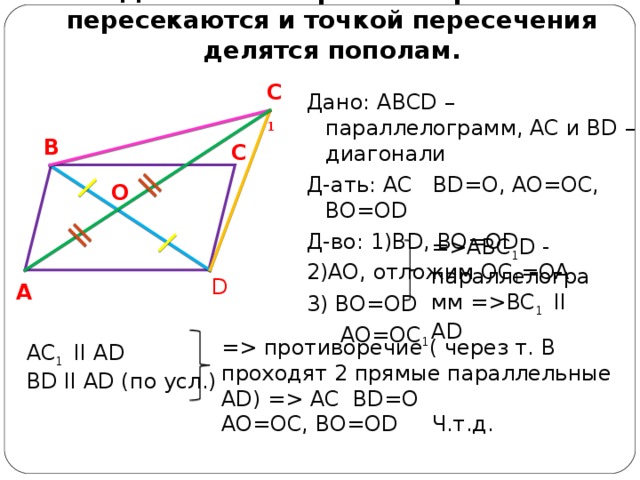
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

C 1

Дано: ABCD – параллелограмм, AC и BD – диагонали

Д-ать: AC BD=O, AO=OC, BO=OD

Д-во: 1) BD, BO=OD

2) AO, отложим OC 1 =OA

3) BO=OD

AO=OC 1

B

C

O

=ABC 1 D - параллелограмм = BC 1 II AD

D

A

= противоречие ( через т. B проходят 2 прямые параллельные AD ) = AC BD=O

AO=OC, BO=OD Ч.т.д.

AC 1 II AD

BD II AD ( по усл.)

AB=DC Аналогично доказывается равенство ∆ BOC= ∆ DOA = AB=DC A D По III признаку ∆ ABC= ∆ CDA = ∟ B= ∟ D Аналогично доказывается равенство ∆ BAD= ∆ CDB = ∟ A= ∟ C 2) AB=CD (по доказанному) BC=AD (по доказанному) AC - общая 3) AB=CD, AD=BC, ∟B=∟D, ∟A=∟C Ч.т.д. " width="640"

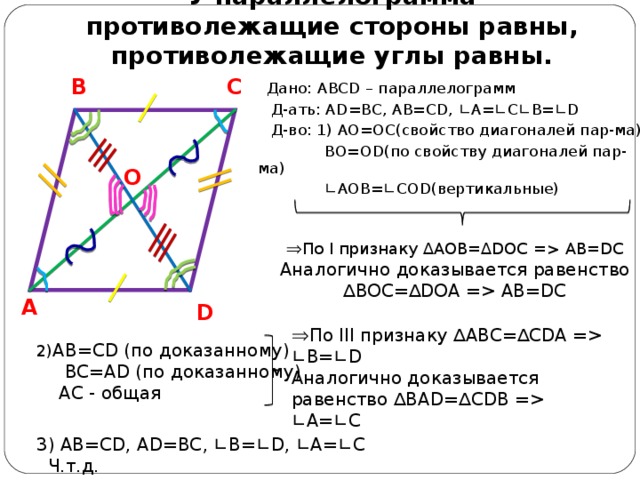
У параллелограмма противолежащие стороны равны, противолежащие углы равны.

С

B

Дано: ABCD – параллелограмм

Д-ать: AD=BC, AB=CD, ∟A=∟C∟B=∟D

Д-во: 1) AO=OC (свойство диагоналей пар-ма)

BO=OD (по свойству диагоналей пар-ма)

∟ AOB= ∟ COD (вертикальные)

O

• По I признаку ∆AOB=∆DOC = AB=DC

Аналогично доказывается равенство ∆ BOC= ∆ DOA = AB=DC

A

D

• По III признаку ∆ ABC= ∆ CDA = ∟ B= ∟ D

Аналогично доказывается равенство ∆ BAD= ∆ CDB = ∟ A= ∟ C

2) AB=CD (по доказанному)

BC=AD (по доказанному)

AC - общая

3) AB=CD, AD=BC, ∟B=∟D, ∟A=∟C Ч.т.д.

По I признаку BAD = CDA = BD = AC Ч. т. д. D A " width="640"

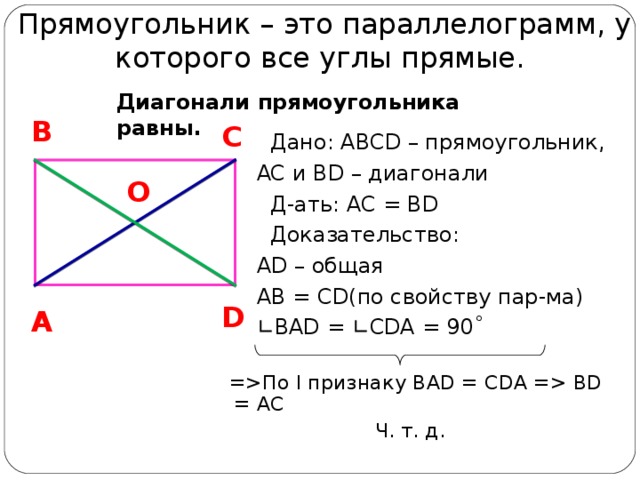
Прямоугольник – это параллелограмм, у которого все углы прямые.

Диагонали прямоугольника равны.

B

C

Дано: ABCD – прямоугольник,

AC и BD – диагонали

Д-ать: AC = BD

Доказательство:

AD – общая

AB = CD( по свойству пар-ма)

∟ BAD = ∟ CDA = 90˚

О

=По I признаку BAD = CDA = BD = AC

Ч. т. д.

D

A

AO – медиана = биссектриса и высота = AO BD = AC BD , AO – биссектриса A и C D 2) ABC – равнобедренный = B = BD – биссектриса B и D Ч.т.д. " width="640"

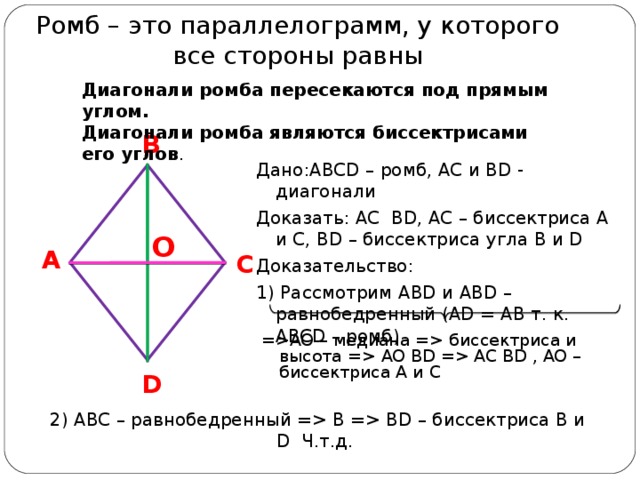
Ромб – это параллелограмм, у которого все стороны равны

Диагонали ромба пересекаются под прямым углом.

Диагонали ромба являются биссектрисами его углов .

B

Дано: ABCD – ромб, AC и BD - диагонали

Доказать: AC BD, AC – биссектриса A и C, BD – биссектриса угла B и D

Доказательство:

1) Рассмотрим ABD и ABD – равнобедренный ( AD = AB т. к. ABCD – ромб)

О

A

C

=AO – медиана = биссектриса и высота = AO BD = AC BD , AO – биссектриса A и C

D

2) ABC – равнобедренный = B = BD – биссектриса B и D Ч.т.д.

Квадрат – это прямоугольник, у которого все стороны равны

C

B

О

D

A

• У квадрата все углы прямые.
• Диагонали квадрата равны.
• Диагонали квадрата пересекаются под прямым углом и являются биссектрисами его углов.

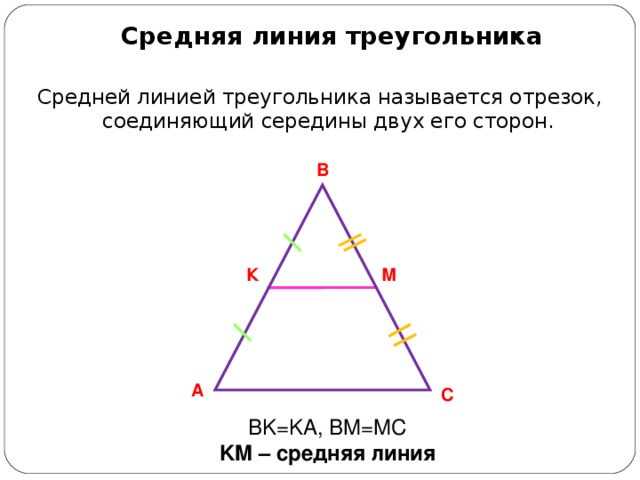
Средняя линия треугольника

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

В

К

М

А

С

BK=KA, BM=MC

KM – средняя линия

a=KD = KD|| AC 2) Проведем прямую DF||AB, по т.Фалеса AF=FC K D a C A F 3) KD AC DF AB =ACDF – параллелограмм = AF=KD 4) AF=FC AF=KC = KD= ½ AC ч.т.д. " width="640"

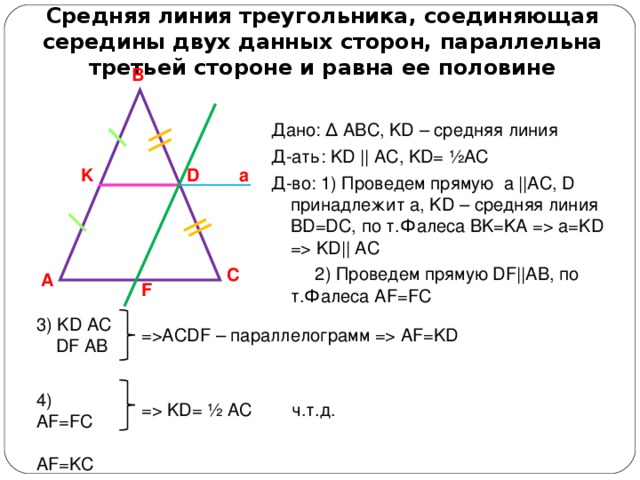
Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине

B

Дано: ∆ ABC, KD – средняя линия

Д-ать: KD || AC, KD= ½AC

Д-во: 1) Проведем прямую a ||AC, D принадлежит a, KD – средняя линия BD=DC, по т . Фалеса BK=KA = a=KD = KD|| AC

2) Проведем прямую DF||AB, по т.Фалеса AF=FC

K

D

a

C

A

F

3) KD AC

DF AB

=ACDF – параллелограмм = AF=KD

4) AF=FC

AF=KC

= KD= ½ AC ч.т.д.