Предел функции в точке

Предел функции в точке

§26 п.2 стр.150

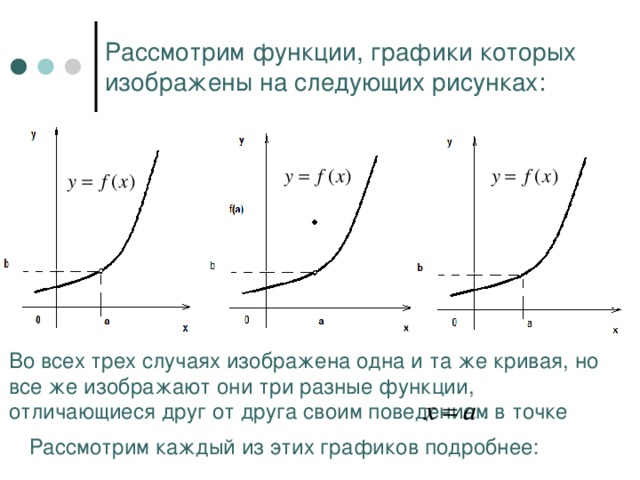
Рассмотрим функции, графики которых изображены на следующих рисунках:

Во всех трех случаях изображена одна и та же кривая, но все же изображают они три разные функции, отличающиеся друг от друга своим поведением в точке

.

Рассмотрим каждый из этих графиков подробнее:

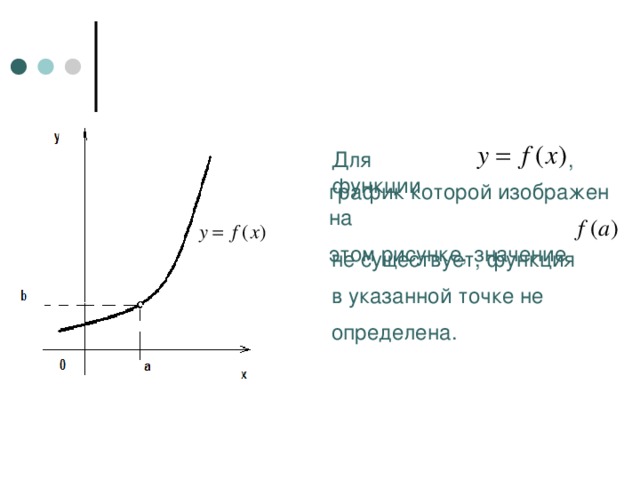
Для функции

,

график которой изображен на

этом рисунке, значение

не существует, функция

в указанной точке не

определена.

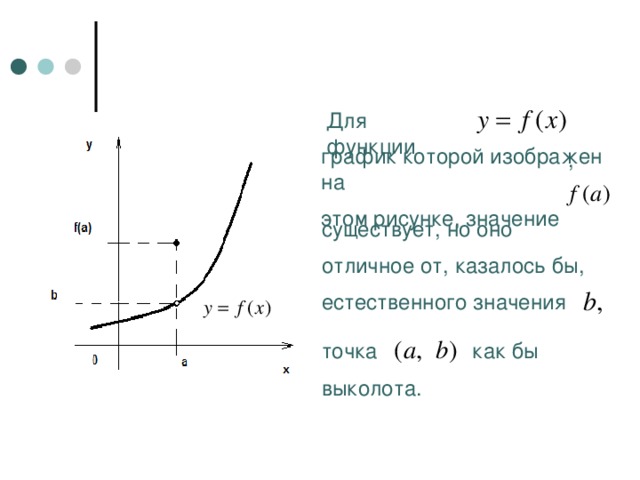
Для функции

график которой изображен на

этом рисунке, значение

,

существует, но оно

отличное от, казалось бы,

естественного значения

точка

как бы

выколота.

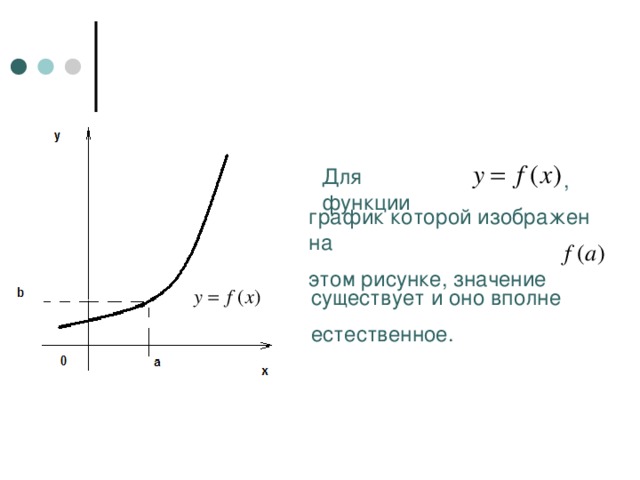
Для функции

,

график которой изображен на

этом рисунке, значение

существует и оно вполне

естественное.

Для всех трех случаев используется одна и та же запись:

которую читают: «предел функции

при стремлении x

к a равен b ».

Содержательный смысл этой фразы следующий: если

значения аргумента выбирать все ближе и ближе к значению

, то значения функции все меньше и меньше

отличаются от предельного значения

Или можно сказать так: в достаточно малой окрестности точки а

справедливо приближенное равенство:

При этом сама точка

исключается из рассмотрения.

Если предел функции

при стремлении х к а равен значению функции в точке х = а , то в таком случае функцию называют непрерывной в точке а .

у = f(x) непрерывна в точке х = а

График такой функции представляет собой

сплошную линию, без «проколов» и «скачков».

Значит непрерывной функцией является функция на третьем рисунке.

Функцию

называют непрерывной

на промежутке

, если она непрерывна в

каждой точке этого промежутка.

Примерами непрерывных функций на всей числовой

прямой являются:

непрерывна на луче

а

Функция

функция

непрерывна на промежутках

А функции

непрерывны на каждом промежутке из области их

определения.

Математики доказали утверждение,

которое мы будем использовать при

вычислении пределов функции в точке:

Если выражение

составлено из

рациональных, иррациональных,

тригонометрических выражений, то функция

непрерывна в любой точке,

в которой определено выражение

Примеры

Вычислить:

Решение.

Выражение

определено в любой точке

в частности, в точке

Следовательно, функция

а потому предел

непрерывна в точке

функции при стремлении

к

равен значению функции в

точке

Имеем:

Решение.

Выражение

определено в любой точке

В частности, в точке

и

за исключением

Следовательно, функция

функция определена.

а потому предел функции при

непрерывна в точке

равен значению функции в точке

стремлении

к

Имеем:

Решение.

Выражение

не определено в точке

поскольку при подстановке этого значения переменной в заданное выражение, то и в числителе, и в знаменателе получится 0 , а на 0 делить нельзя.

Однако, заданную алгебраическую дробь можно сократить

и

тождественны при условии

Значит, функции

саму

Но при вычислении предела функции при

точку

можно исключить из рассмотрения (об этом

говорилось выше). Поэтому:

Пример 3, 4 и 5 стр. 152 (учебник)

Пример 6 стр. 153 самостоятельно