Просмотр содержимого документа
«Приближенное вычисление определенных интегралов»
ББК 22.21
ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
А.С. Тирский, старший преподаватель кафедры «Естетственных и технических наук»,
Ю. И. Вазиков, студент группы Мех 09 Олёкминский филиал
ФГБОУ ВПО Якутская ГСХА»,, г. Олёкминск
Как известно, некоторые функции не интегрируются в классе элементарных функций. В таком случае первообразную можно получить в виде степенного ряда путем почленного интегрирования ряда Тейлора подъинтегральной функции f(t) в окрестности точки 
Поставим перед собой задачу: вычислить неберущийся определенный интеграл с помощью степенных рядов  с определенной степенью точности и сделаем предположение, что функция разлагается в степенной ряд по степеням х и отрезок
с определенной степенью точности и сделаем предположение, что функция разлагается в степенной ряд по степеням х и отрезок 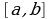 принадлежит интервалу сходимости.
принадлежит интервалу сходимости.
Пусть Ф(х) – первообразная для f(x) ,  = Ф(в)-Ф(а), где значения Ф(в) и Ф(а) вычислены приближенно.
= Ф(в)-Ф(а), где значения Ф(в) и Ф(а) вычислены приближенно.
Ограничимся n членами разложения первообразной Ф(х). Следовательно


где  - частичная сумма разложения первообразной Ф(х).
- частичная сумма разложения первообразной Ф(х).
Так как Ф(в)-Ф(а) = 
Значит абсолютная погрешность этой формулы не превышает суммы:
 (1)
(1)
Сделаем важное замечание: Практически оценкой (1) не пользуются, так как они очень завышены. Удобнее вычислять Ф(а) и Ф(в) отдельно, как суммы соответствующих числовых рядов. Может так случиться, что для достижения указанной точности, при вычислении значений Ф(а) и Ф(в) требуется ограничиться отдельным количеством членов полученного ряда.
Теперь рассмотрим несколько примеров.
Вычислить приближенно: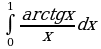 с точностью до 0,01
с точностью до 0,01
Решение:
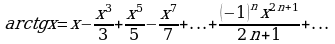
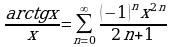
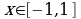
Интегрируя обе части равенства на отрезке  , лежащем внутри интервала сходимости
, лежащем внутри интервала сходимости 
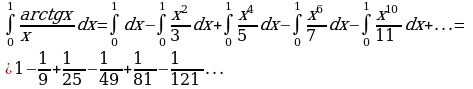
Так как 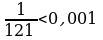 ,то
,то 
Рассмотрим еще один пример
Вычислить 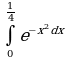 с точностью до 0,001
с точностью до 0,001
Решение: Заменяя в известной формуле х на -х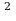 разложим подъинтегральную функцию в ряд Маклорена.
разложим подъинтегральную функцию в ряд Маклорена.
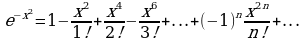

Интегрируя обе части равенства на отрезке  , лежащем внутри промежутка сходимости, получим
, лежащем внутри промежутка сходимости, получим

получили ряд лейбницкого типа. Так как 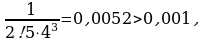 а
а  то с точностью до 0,001 имеем
то с точностью до 0,001 имеем 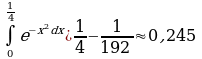
Таким образом, получаем один способов вычисления «неберущихся» интегралов.
Литература:
Шипачев В.С. Задачник по высшей математике: Учебное пособие для вузов – М. Высшая школа, 2001.- 345с.
Шипачев В.С. Основы высшей математики: Учебное пособие для вузов – М: Высшая школа, 1998.- 380с.
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, в 2-х частях Ч.1,Ч.2.:Учебн. пособие для вузов – М.: Высшая школа, 1999.- 280с.








 с определенной степенью точности и сделаем предположение, что функция разлагается в степенной ряд по степеням х и отрезок
с определенной степенью точности и сделаем предположение, что функция разлагается в степенной ряд по степеням х и отрезок 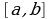 принадлежит интервалу сходимости.
принадлежит интервалу сходимости.
 - частичная сумма разложения первообразной Ф(х).
- частичная сумма разложения первообразной Ф(х).
 (1)
(1)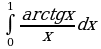 с точностью до 0,01
с точностью до 0,01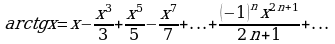
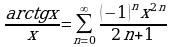
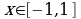
 , лежащем внутри интервала сходимости
, лежащем внутри интервала сходимости 
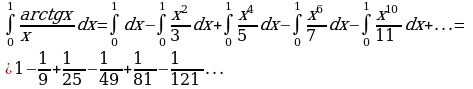
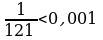 ,то
,то 
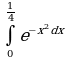 с точностью до 0,001
с точностью до 0,001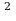 разложим подъинтегральную функцию в ряд Маклорена.
разложим подъинтегральную функцию в ряд Маклорена.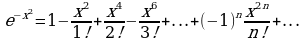

 , лежащем внутри промежутка сходимости, получим
, лежащем внутри промежутка сходимости, получим
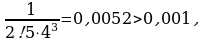 а
а  то с точностью до 0,001 имеем
то с точностью до 0,001 имеем