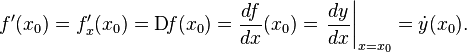Просмотр содержимого документа
«ПРАКТИЧЕСКАЯ РАБОТА Вычисление производных»
ПРАКТИЧЕСКАЯ РАБОТА
Вычисление производных
Цель: совершенствовать умения вычислять производные элементарных функций.
Методические указания и теоретические сведения к практической работе
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование.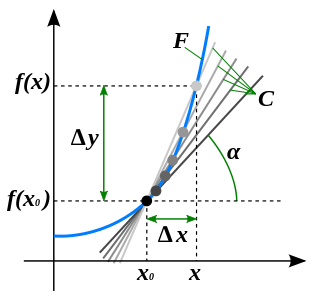
Иллюстрация понятия производной
Определение производной функции через предел
Пусть в некоторой окрестности точки 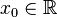 определена функция
определена функция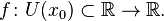 Производной функции
Производной функции 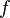 в точке
в точке 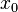 называется предел, если он существует,
называется предел, если он существует,
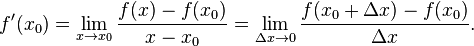
Общепринятые обозначения производной функции
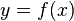
в точке
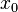
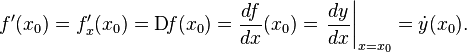
Заметим, что последнее обычно обозначает производную по времени (в теоретической механике).
Таблица производных
| Производные степенных функций | Производные тригонометрических функций | Производные обратных тригонометрических функций |
| 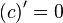
| 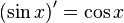
| 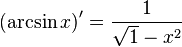
|
| 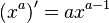
| 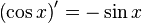
| 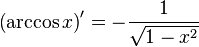
|
| 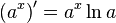
| 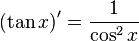
| 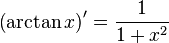
|
| 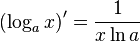
| 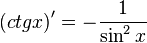
| 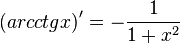
|
|
|
|
|
|
|
|
|
|
|
|
|
Правила дифференцирования
Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
Геометрический смысл производной
На графике функции выбирается абсцисса x0 и вычисляется соответствующая ордината f(x0). В окрестности точки x0 выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C5). Расстояние Δx = x — x0 устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии C5 — C1). Тангенс угла α наклона этой касательной — и есть производная в точке x0.
Пример №1. Найти производную функции .
Решение. .
Пример №2. Найти производную функции  и вычислить ее значения в точках
и вычислить ее значения в точках  и
и 
Решение.
Пример №3. Найти производную функции .
Решение.
Пример №4. Найти производную функции .
Решение.
ЗАДАНИЕ ДЛЯ ВЫПОЛНЕНИЯ
Найдите производные следующих функций:
 ;
;
;
Найдите производные следующих функций:
 ;
;
 ;
;
;
 ;
;

Вычислите значение производной:
 ;
;
 ;
; 
Вычислите значение производной:
 ;
; 
Найдите производную следующих функций:

Найдите производные следующих функций:
 ;
;

Найдите производные следующих функций:
 ;
;
Найдите производные следующих функций:
;
 ;
;
 .
.
2