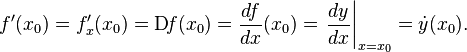Просмотр содержимого документа
«Практическая работа «Вычисление производных функций».»
Практическое занятие
Тема: «Математический анализ».
Наименование работы: «Вычисление производных функций».
Цель: совершенствовать умения вычислять производные функций.
Содержание
Часть 1. Теоретическая
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование.
Иллюстрация понятия производной
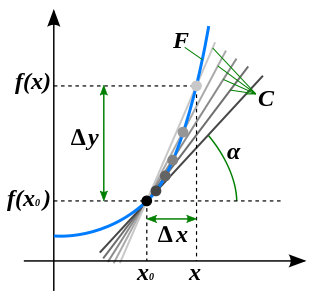
Определение производной функции через предел
Пусть в некоторой окрестности точки 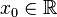 определена функция
определена функция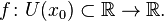 Производной функции
Производной функции 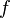 в точке
в точке 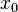 называется предел, если он существует,
называется предел, если он существует,
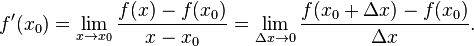
Общепринятые обозначения производной функции
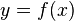
в точке
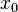
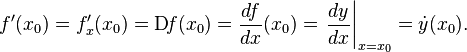
Заметим, что последнее обычно обозначает производную по времени (в теоретической механике).
Таблица производных
| Производные степенных функций | Производные тригонометрических функций | Производные обратных тригонометрических функций |
| 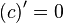
| 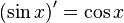
| 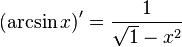
|
| 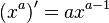
| 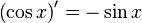
| 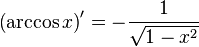
|
| 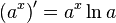
| 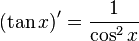
| 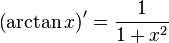
|
| 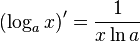
| 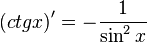
| 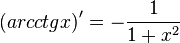
|
Правила дифференцирования
Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
Пример: Найти производную функции .
Решение. .
Пример: Найти производную функции  и вычислить ее значения в точках
и вычислить ее значения в точках  и
и 
Решение.
Пример: Найти производную функции .
Решение.
Пример: Найти производную функции .
Решение.
Часть 2. Практическая
Задание: Вычислите производные следующих функций:
| № | Задание | № | Задание |
| 1 | а) у = , б) у= , б) у= , , в) у= г) y = г) y =  | 6 | а) у=  , б) у= , б) у= , в) г) y = ln(1 + cosx) , в) г) y = ln(1 + cosx) |
| 2 | а) у=  б) у= б) у= , , в)  , г) y = , г) y =  | 7 | а) у= б) у= , в) у= , в) у= , г) y = 2sin5x – cos2x , г) y = 2sin5x – cos2x |
| 3 | а) у =  б) у= б) у= в)  г) y = г) y =  | 8 | а) у= б) у= , в) , в)  , г) y = tg( , г) y = tg( ) ) |
| 4 | а) у =  , б) у= , б) у= , в) в) , в) в)  , г) y = , г) y =  | 9 | а) у=  , б) у= , б) у= , , в)  г) y = lntg5x г) y = lntg5x |
| 5 | а) у =  , б) у= , б) у= , в) у= , в) у= , г) y = lnsinx , г) y = lnsinx | 10 | а) у=  б) у= б) у= , в) , в)  , г) y= , г) y=  |
Вопросы к практическому занятию
Дайте определение производной.
Как называется действие нахождение производной?
Запишите формулу производной суммы.
Запишите формулу производной произведения.
Запишите формулу производной частного.
Чему равна производная константы.
Выучите формулы производных элементарных функций.
Как вычислить производную сложной функции?