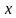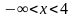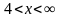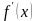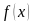Практическое занятие
Тема: «Производная и ее приложения».
Наименование работы: «Решение прикладных задач в области профессиональной деятельности с применением производной и на построение графиков функций».
Цель: формирование умений исследовать функции при помощи производной, применять производную при решении задач на максимум и минимум.
Содержание
Часть 1. Теоретическая
Возрастание и убывание функции
Функция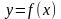 называется возрастающей в промежутке
называется возрастающей в промежутке 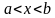 , если для любых
, если для любых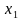 и
и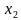 , принадлежащих этому промежутку и таких, что
, принадлежащих этому промежутку и таких, что 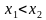 , имеет место неравенство
, имеет место неравенство 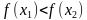 .
.
Функция 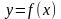 называется убывающей в промежутке
называется убывающей в промежутке 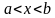 , если для любых
, если для любых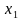 и
и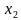 , принадлежащих этому промежутку и таких, что
, принадлежащих этому промежутку и таких, что 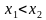 , имеет место неравенство
, имеет место неравенство 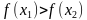 .
.
Как возрастающие , так и убывающие функции называются монотонными, а промежутки, в которых функция возрастает или убывает, - промежутками монотонности.
Возрастание и убывание функции 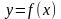 характеризуется знаком ее производной:
характеризуется знаком ее производной:
- если в некотором промежутке 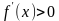 , то функция возрастает в этом промежутке;
, то функция возрастает в этом промежутке;
- если в некотором промежутке 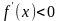 , то функция убывает в этом промежутке.
, то функция убывает в этом промежутке.
Пример: Найти промежутки монотонности следующих функций:
а)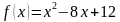 б)
б)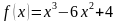
а) Находим производную: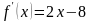 , имеем
, имеем 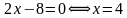 .
.
Последующие рассуждения представим в таблице:
Таким образом, данная функция в промежутке 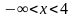 убывает,
убывает,
а в промежутке 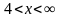 возрастает.
возрастает.
б)
Составим таблицу:
Итак, в промежутках  и
и 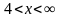 функция возрастает, а в промежутке
функция возрастает, а в промежутке  - убывает.
- убывает.
Исследование функции на экстремум с помощью первой производной
Точка  из области определения функции
из области определения функции 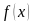 называется точкой минимума этой функции, если существует такая
называется точкой минимума этой функции, если существует такая  – окрестность точки
– окрестность точки  , что для всех
, что для всех  из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 
Точка  из области определения функции
из области определения функции  называется точкой максимума этой функции, если существует такая
называется точкой максимума этой функции, если существует такая  – окрестность точки
– окрестность точки  , что для всех
, что для всех  из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 
Точки минимума и максимума функции называются точками экстремума данной функции, а значения функции в этих точках – минимумом и максимумом (или экстремумами) функции.
Точками экстремумами могут служить только критические точки, т.е. точки, принадлежащие области определения функции, в которых производная 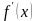 обращается в нуль или терпит разрыв.
обращается в нуль или терпит разрыв.
Если при переходе через критическую точку  производная
производная 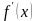 меняет знак, то функция
меняет знак, то функция  имеет в точке
имеет в точке  экстремум: минимум в том случае, когда производная меняет знак с минуса на плюс, и максимум – когда с плюса на минус. Если же при переходе через критическую точку
экстремум: минимум в том случае, когда производная меняет знак с минуса на плюс, и максимум – когда с плюса на минус. Если же при переходе через критическую точку  производная
производная 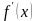 не меняет знака, то функция
не меняет знака, то функция  в точке
в точке  не имеет экстремума.
не имеет экстремума.
Правило нахождения экстремумов функции  с помощью первой производной
с помощью первой производной
Найти производную 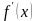 .
.
Найти критические точки функции  , т.е. точки в которых
, т.е. точки в которых 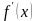 обращается в нуль или терпит разрыв.
обращается в нуль или терпит разрыв.
Исследовать знак производной 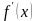 в промежутках, на которые найденные критические точки делят область определения функции
в промежутках, на которые найденные критические точки делят область определения функции  . При этом критическая точка
. При этом критическая точка  есть точка минимума, если она отделяет промежуток, в котором
есть точка минимума, если она отделяет промежуток, в котором  , от промежутка, в котором
, от промежутка, в котором  , и точка максимума – в противном случае. Если же в соседних промежутках, разделенных критической точкой
, и точка максимума – в противном случае. Если же в соседних промежутках, разделенных критической точкой  , знак производной не меняется, то в точке
, знак производной не меняется, то в точке  функция экстремума не имеет.
функция экстремума не имеет.
Вычислить значения функции в точках экстремума
Пример: Исследовать на экстремум следующие функции:
а) б)
б) 
а) Находим  , приравняем производную к нулю, имеем
, приравняем производную к нулю, имеем  . Получим единственную критическую точку
. Получим единственную критическую точку  .
.
Последующие рассуждения представим в таблице:
График функции  есть парабола. Точка минимума (2;-4) является вершиной параболы.
есть парабола. Точка минимума (2;-4) является вершиной параболы.
б) Находим  , приравняем производную к нулю, имеем
, приравняем производную к нулю, имеем . Получим две критические точки
. Получим две критические точки  и
и  .
.
Последующие рассуждения представим в таблице:
| 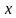
| 
| 0 | 
| 2 | 
|
| 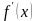
| + | 0 | - | 0 | + |
| 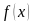
| 
| Максимум 
| 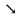
| Минимум 
| 
|
Наименьшее и наибольшее значения функции
Для нахождения наименьшего и наибольшего значений функции, непрерывной в некотором промежутке, необходимо:
Найти критические точки, принадлежащие заданному промежутку, и вычислить значения функции в этих точках;
Найти значения функции на концах промежутка;
Сравнить полученные значения; тогда наименьшее и наибольшее из них являются соответственно наименьшим и наибольшим значениями функции в рассматриваемом промежутке.
Пример: Найти наименьшее и наибольшее значение функции  в промежутке
в промежутке  .
.
Имеем  ; 2
; 2 , т.е.
, т.е.  - критическая точка. Находим
- критическая точка. Находим  ; далее, вычисляем значения функции на концах промежутка:
; далее, вычисляем значения функции на концах промежутка:  ,
,  .
.
Итак, наименьшее значение функции равно - 1 и достигается ею во внутренней точке промежутка, а наибольшее значение равно 3 и достигается на левом конце промежутка.
Построение графиков функций
Общая схема построения графиков функций
Найти область определения функции.
Выяснить, не является ли функция четной, нечетной или периодической.
Найти точки пересечения графика с осями координат (если это не вызывает затруднений).
Найти асимптоты графика функции.
Найти промежутки монотонности функции и ее экстремумы.
Найти промежутки выпуклости графика функции и точки перегиба.
Построить график, используя полученные результаты исследования.
Пример: Построить график функции .
Функция определена на всей числовой прямой, т.е.  .
.
Данная функция не является ни четной, ни нечетной; кроме того, она не является периодической.
Найдем точку пересечения графика с осью  : полагая
: полагая  , получим
, получим  . Точки пересечения графика с осью
. Точки пересечения графика с осью  в данном случае найти затруднительно.
в данном случае найти затруднительно.
Очевидно, что график функции не имеет асимптот.
Найдем производную:  . Далее, имеем .
. Далее, имеем .
Точки  и
и  делят область определения функции на три промежутка:
делят область определения функции на три промежутка:  ,
,  ,
,  . В промежутках
. В промежутках  и
и  , то есть функция возрастает, а в промежутке
, то есть функция возрастает, а в промежутке 
 , то есть функция убывает. При переходе через точку
, то есть функция убывает. При переходе через точку  производная меняет знак с плюса на минус, а при переходе через точку
производная меняет знак с плюса на минус, а при переходе через точку  - с минуса на плюс. Значит, .
- с минуса на плюс. Значит, .
Найдем вторую производную: . Точка  делит область определения функции на два промежутка
делит область определения функции на два промежутка  и
и  . В первом из них
. В первом из них  , а во втором
, а во втором
 , то есть в промежутке
, то есть в промежутке  кривая выпукла вверх, а в промежутке
кривая выпукла вверх, а в промежутке  выпукла вниз. Таким образом, получим точку перегиба (2;-1).
выпукла вниз. Таким образом, получим точку перегиба (2;-1).
Используя полученные данные, строим искомый график.
Часть 2. Практическая
Задание: Исследовать функцию y = f(x). Построить график функции y = f(x).
| № | Задание | № | Задание |
| 1 | y =  | 6 | y =  |
| 2 | y =  | 7 | y =  |
| 3 | y =  | 8 | y =  |
| 4 | y =  + + | 9 | y = 
|
| 5 | y = 12x -  | 10 | у =  |
Вопросы к практическому занятию
Функция называется возрастающей в промежутке, если…
Функция называется убывающей в промежутке, если...
Что называется точкой минимума функции?
Что называется точкой максимума?
Что называется точками экстремума?
Сформируйте правило нахождения экстремумов функции с помощью первой производной.
Что необходимо сделать для нахождения наименьшего и наибольшего значений функции, непрерывной в некотором промежутке?
Назовите общую схему построения графиков функций.







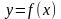 называется возрастающей в промежутке
называется возрастающей в промежутке 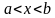 , если для любых
, если для любых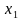 и
и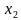 , принадлежащих этому промежутку и таких, что
, принадлежащих этому промежутку и таких, что 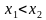 , имеет место неравенство
, имеет место неравенство 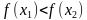 .
.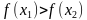 .
.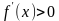 , то функция возрастает в этом промежутке;
, то функция возрастает в этом промежутке; 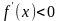 , то функция убывает в этом промежутке.
, то функция убывает в этом промежутке. 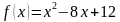 б)
б)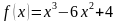
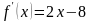 , имеем
, имеем 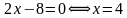 .
.