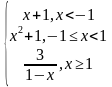Просмотр содержимого документа
«Практическое занятие «Исследование функции на непрерывность».»
Практическое занятие
Тема: «Математический анализ».
Наименование работы: «Исследование функции на непрерывность».
Цель: сформировать умение исследовать функцию на непрерывность и наличие точек разрыва, определять род точек разрыва.
Содержание
Часть 1. Теоретическая
Функция f(х) называется непрерывной в точке х0, если она определена в некоторой окрестности этой точки и lim f(х) = f(х0)
х→0
Равенство из определения непрерывности функции означает выполнение трех условий:
1) функция f(х) определена в точке х0 и в ее окрестности;
2) функция f(х) имеет предел при х→х0;
3) предел функции в точке х0 равен значению функции в этой точке, т.е. выполняется равенство из определения непрерывности функции.
Точка разрыва функции
Пусть точка х0 принадлежит области определения функции f(х) или является граничной точкой этой области. Точка х0 называется точкой разрыва функции f(х), если f(х) не является непрерывной в этой точке.
| Точка разрыва функции |
| первого рода | второго рода |
| если в этой точке существуют конечные пределы функции слева и справа lim f(х) и lim f(х); х→х0-0 х→х0+0 при этом: | если по крайней мере один из односторонних пределов lim f(х) или х→х0-0 lim f(х) не существует х→х0+0 или равен бесконечности
|
| если lim f(х)=lim f(х), х→х0-0 х→х0+0 то х0 – точка устранимого разрыва | если lim f(х)≠lim f(х), х→х0-0 х→х0+0 то х0 – точка конечного разрыва . │lim f(х)-lim f(х)│, х→х0-0 х→х0+0 скачок функции |
Пример: Найти точки разрыва функции, выяснить их типы. Для функции f(х)={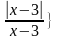 , найти точки разрыва, выяснить их тип.
, найти точки разрыва, выяснить их тип.
Решение. Функция f(х) определена и непрерывна на всей числовой оси, кроме точки х=3. Очевидно, f(х) =  Значит, lim f(х)= 1, а
Значит, lim f(х)= 1, а
х→3+0
lim f(х) = -1. Поэтому в точке х=3 функция имеет разрыв первого рода.
х→3-0
Скачок функции в этой точке равен 1-(-1)=2.
Часть 2. Практическая
Задание: Исследуйте функции на непрерывность.
| № | Задание | № | Задание |
| 1 | у=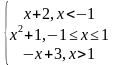 у=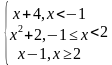 | 6 | у=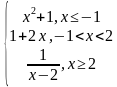 у= у=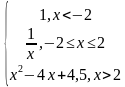 |
| 2 | у=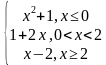 у=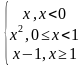 | 7 | у=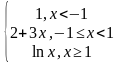 , , у=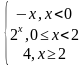 |
| 3 | у=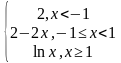 у= у=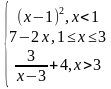 | 8 | у=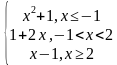 у= у=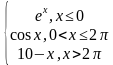 |
| 4 | у=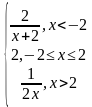 у= у=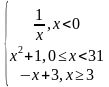 | 9 | у=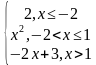 у=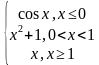 |
| 5 | у=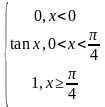 ,у= ,у=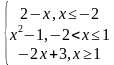 | 10 | у=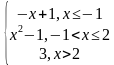 у= у=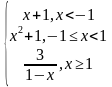 |
Вопросы к практическому занятию
Непрерывность функции в точке.
Условия непрерывности функции в точке.
Что такое точка разрыва первого рода?
Что такое точка разрыва второго рода?
Что такое точка устранимого разрыва?







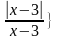 , найти точки разрыва, выяснить их тип.
, найти точки разрыва, выяснить их тип.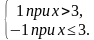 Значит, lim f(х)= 1, а
Значит, lim f(х)= 1, а 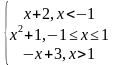
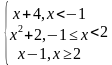
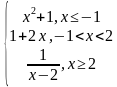 у=
у=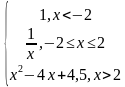
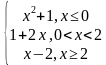
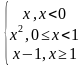
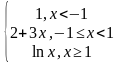 ,
, 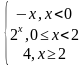
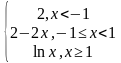 у=
у=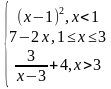
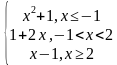 у=
у=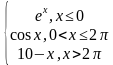
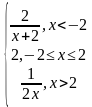 у=
у=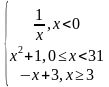
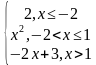
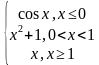
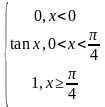 ,у=
,у=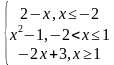
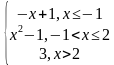 у=
у=