Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
 «Оренбургский государственный педагогический университет»
«Оренбургский государственный педагогический университет»
Физико-математический факультет
Оренбургского государственного педагогического университета
Кафедра алгебры, геометрии и истории математики
КУРСОВАЯ РАБОТА
по дисциплине: геометрия
«Геометрия плоских фигур на плоскости Лобачевского»
Направление подготовки: Дополнительная профессиональная программа профессиональной переподготовки
Профиль подготовки: математика
Форма обучения: заочная
Выполнила студентка:
Верховцева Татьяна Павловна
II курс, группа-математика
Научный руководитель:
Прояева Ирина Владимировна
К.ф.м.н., доцент
________________ _____________
оценка подпись
«___» ____________ 201.. г.
Оренбург, 2017год
Оглавление
I.Введение………………………………………………….…………………3
II.Теоретические аспекты геометрии Лобачевского:
II.1.История создания неевклидовой геометрии Лобачевского ………… 5
II.2.Основная аксиома геометрии Лобачевского…………………………..8
II.3. Теорема о существовании параллельных прямых…………………...11
II.4.Треугольники и четырехугольники на плоскости
Лобачевского……..…………………………………………………..…...…14
II.5. Дефект треугольника и многоугольника…………………………….17
III.Практическое применение геометрии Лобачевского:
III.1.Теорема Пифагора…… ……….………………………………..……..18
1.а Замечание к теореме Пифагора…………… ………………...……19
III.2.Площадь треугольника………… ………...…………..….…………..19
III.3. Применение геометрии Лобачевского в точных науках………..…20
III.4. Анализ состава исторической справки о Н.И. Лобачевском в
школьном курсе математики……………………………………………….21
IV.Заключение……………………………………………………….………23
V.Список литературы............................................................................……..24
Приложение………………………………………………………………….26
I.Введение
Геометрия – это одна из самых древнейших наук. Она зародилась в Древнем Египте как набор правил для решения практических задач, возникающих при строительстве, при распределении земельных участков, измерении объемов, площадей и других величин. Древнегреческий ученый Эдем Родосский в IV веке до нашей эры писал: «Геометрия была открыта египтянами, и возникла при измерении Земли. Это измерение было им необходимо вследствие разлития реки Нил, постоянно смывавшей границы. Нет ничего удивительного, что эта наука, как и другие, возникла из потребности человека.»
Как наука, геометрия впервые сформировалась в Древней Греции, когда геометрические закономерности и зависимости, найденные ранее опытным путем, были приведены в надлежащую систему и доказаны. Основные достижения в области математики были систематизированы около 300 лет до н.э. греческим ученым Евклидом и изложены в его знаменитом труде «Начала», состоящем из тринадцати книг. Это сочинение является первым дошедшим до нас строгим логическим построением геометрии. «Начала» Евклида служили на протяжении более 2000 лет образцом строгого дедуктивного изложения геометрии.
Однако развитие геометрии не стояло на месте. Ученые стремились найти пути логически безупречного построения геометрии. Все чаще они обращались к доказательству постулатов геометрии Евклида. Самым противоречивым ученые считали пятый постулат геометрии Евклида. Попытки вывести его из остальных постулатов и аксиом длились более двух тысяч лет, но были безуспешными. В это время были сформулированы и доказаны теоремы, которые раскрывали новые свойства геометрических фигур.
Одним из первых ученых 19 века, кто построил геометрию, отличную от евклидовой геометрии, стал профессор Казанского университета Н.И.Лобачевский. Именно он дал начало новой неевклидовой геометрии, чаще всего называемой геометрией Лобачевского. Она основана на тех же основных посылках, что и евклидова геометрия, за исключением аксиомы о параллельных.
Я выбрала именно тему «Геометрия плоских фигур на плоскости Н.И. Лобачевского». Данная тема интересна мне по нескольким причинам: теория геометрии Лобачевского помогает взглянуть по-другому на окружающий нас мир, это интересный, необычный и прогрессивный раздел современной геометрии, который дает материал для размышлений – в ней не все просто, не все ясно с первого взгляда, чтобы ее понять, нужно обладать фантазией и пространственным воображением. Да и известные каждому плоские фигуры евклидовой геометрии, вероятно, будут вести себя несколько по-другому.
Итак, целью моей работы является изучение материалов геометрии Лобачевского, связанных с геометрией плоских фигур, на примере треугольника и четырехугольника.
Задачами моей курсовой работы являются:
Познакомиться с историей создания геометрии Лобачевского;
Выяснить, какие постулаты являются основополагающими в геометрии Лобачевского;
Исследовать геометрию плоских фигур на плоскости Лобачевского;
Проработать практическое применение и ценность данной геометрии.
II. Теоретические аспекты геометрии Лобачевского
II.1.История создания неевклидовой геометрии Лобачевского
Со времен Евклида геометрию считали аксиоматически построенной математической наукой. Все содержание евклидовой геометрии было построено на системе аксиом. Однако, аксиома параллельных была единственной аксиомой, доказательство которой занимало умы математиков более чем два тысячелетия. Оказалось то, что пятый постулат не зависит от предыдущих. И в начале XIX века, почти одновременно сразу у нескольких математиков: у К. Гаусса в Германии, у Я. Больяи в Венгрии и у Н. Лобачевского в России, возникла мысль о существовании геометрии, в которой верна аксиома, заменяющая пятый постулат: на плоскости через точку, не лежащую на данной прямой, проходят, по крайней мере, две прямые, не пересекающие данную. Лобачевский, созданием своей геометрии, доказал невозможность логического вывода пятой евклидовой аксиомы. И в 1829 году в своей работе по неевклидовой геометрии «О началах геометрии» он заявил о том, что «допущение постулата, противоположного постулату Евклида, позволяет построить геометрию столь же содержательную, как и евклидова, и свободную от противоречий». Это вызвало множество негативных откликов со стороны современников. Несмотря на это, Лобачевский продолжил отстаивать свои геометрические идеи на протяжении всей своей жизни.
Основой теории Лобачевского можно считать его слова: «Геометрия зависит от форм движения материальных тел.», то есть аксиомы планиметрии можно рассматривать не только на плоскости, но и в пространстве. Сам Лобачевский называл свою геометрию «воображаемой», хотя доказательство непротиворечивости теории пространственных отношений было дано, когда были указаны ее интерпретации(модели).
Выделяют три различные модели геометрии Лобачевского:
1) Модель Пуанкаре
2) Модель Клейна
3) Отображение геометрии Лобачевского на псевдосфере (интерпретация Бельтрами)
1) Модель Пуанкаре.
В модели Пуанкаре на евклидовой плоскости E фиксируется горизонтальная прямая x. Она носит название «абсолюта». Точками плоскости Лобачевского считаются точки плоскости E, лежащие выше абсолюта x. Таким образом, в модели Пуанкаре плоскость Лобачевского – это полуплоскость L, лежащая выше абсолюта.
Прямыми плоскости L считаются полуокружности с центрами на абсолюте или лучи с вершинами на абсолюте и перпендикулярные ему.
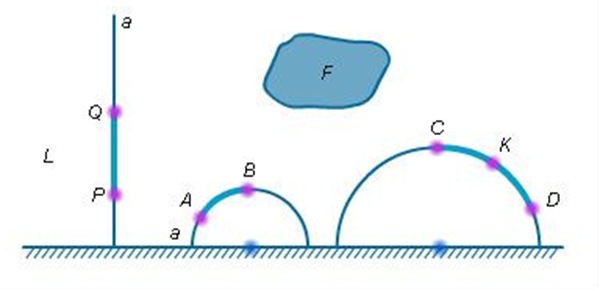 Рис. 1
Рис. 1
2) Модель Клейна.
За плоскость принимается какой-либо круг (рис. 2.1), за точки - точки принадлежащие этому кругу, за прямые - хорды - конечно, с исключением концов, поскольку рассматривается только внутренность круга. За перемещения принимаются преобразования круга, переводящие его в себя и хорды - в хорды. Соответственно, "конгруэнтными" называются фигуры, переводимые друг в друга такими преобразованиями.
 Рис. 2
Рис. 2
Очевидно, что в пределах определенной части плоскости (круга), как бы эта часть не была велика, можно провести через данную точку С множество прямых, не пересекающих данной прямой. Внутри круга любого конечного радиуса существует множество прямых (т.е. хорд), проходящих через т. С и не встречающих прямой АВ (рис. 2.2). Всякая теорема планиметрии Лобачевского является в этой модели теоремой геометрии Евклида и, обратно, всякая теорема геометрии Евклида, говорящая о фигурах внутри данного круга, является теоремой геометрии Лобачевского.
3) Отображение геометрии Лобачевского на псевдосфере (интерпретация Бельтрами)
Э. Бельтрами показал в своей работе «Опыт интерпретации неевклидовой геометрии» (1868г.), что наряду с плоскостями, на которых осуществляется евклидова геометрия, и сферическими поверхностями, на которые действуют формулы сферической геометрии, существуют и такие реальные поверхности, названные им псевдосферами (рис.3), на которых частично осуществляется планиметрия Лобачевского.
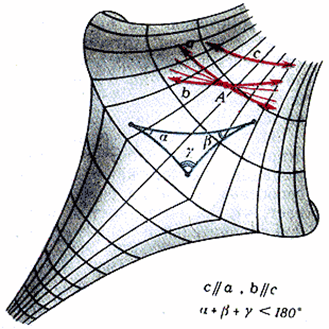 Рис. 3
Рис. 3

 Рис.4
Рис.4
Известно, что сферу можно получить вращением полуокружности вокруг своего диаметра. Подобно тому, псевдосфера образуется вращением линии FCE, называемой трактрисой, вокруг ее оси АВ (рис.4). То есть, псевдосфера – это поверхность в обыкновенном реальном пространстве, на котором выполняются многие аксиомы и теоремы неевклидовой планиметрии Лобачевского.
Таким образом, Лобачевский еще раз доказал, что его геометрия тесно связана со сферической геометрией. В сферической геометрии можно рассматривать треугольники, многоугольники, окружности, выводить формулы для длины окружности, площади круга, выводить соотношения между сторонами и углами треугольников, аналогичные теоремам синусов и косинусов, формулу, связывающую сумму углов с его площадью. Но во все эти формулы будет входить радиус данной сферы. А, если этот радиус сферы заменить на мнимое число, то они превратятся в формулы геометрии Лобачевского.
II.2.Основная аксиома геометрии Лобачевского.
Я упоминала о том, что геометрия Лобачевского основана на I-IV аксиомах евклидовой геометрии и на аксиоме выведенной самим Лобачевским:
Пусть а — произвольная прямая, а A — точка, не лежащая на этой прямой. Тогда в плоскости, определяемой точкой А и прямой а, существует не менее двух прямых, проходящих через точку А и не пересекающих прямую а.
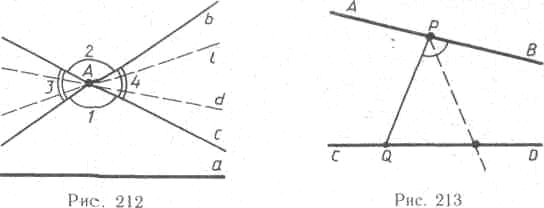
рис 1 рис 2
Из данной аксиомы следует, что если даны произвольная прямая а и точка А, не лежащая на ней, то существует бесконечное множество прямых, проходящих через точку А и не пересекающих прямую а. В самом деле, существуют две прямые, которые мы обозначим через b и с, проходящие через точку А и не пересекающие прямую а (рис. 1). Прямые b и с образуют две пары вертикальных углов, которые на рисунке 1 обозначены цифрами 1, 2 и 3, 4. Прямая а не пересекает прямые b и с, поэтому все ее точки принадлежат внутренней области одного из четырех углов 1, 2, 3, 4, например внутренней области угла 1. Тогда, очевидно, любая прямая, проходящая через точку А и лежащая внутри вертикальных углов 3 и 4, не пересекает прямую а (например, прямые L и d на рис. 1).
Условимся считать, что все прямые, рассматриваемые нами, являются направленными прямыми.
Прямая АВ называется параллельной прямой CD, если эти прямые не имеют общих точек и, каковы бы ни были точки Р и Q, лежащие соответственно на прямых АВ и CD, любой внутренний луч1 угла QPB пересекает луч QD (рис. 2). Если прямая АВ параллельна прямой CD, то пишут так: AB||CD.
Имеет место следующий признак параллельности прямых.
Теорема 1. Если прямые АВ и CD не имеют общих точек и существуют точки Р и Q, такие, что Р  АВ и Q
АВ и Q  CD, и любой внутренний луч угла QPB пересекает луч QD, то AB||CD.
CD, и любой внутренний луч угла QPB пересекает луч QD, то AB||CD.
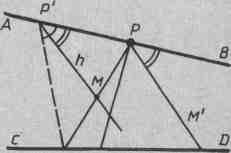
Для доказательства теоремы достаточно установить, что, каковы бы ни были точки Р' и Q', лежащие соответственно на прямых АВ и CD, любой внутренний луч h угла Q'P'B пересекает луч Q'D. Возможны три случая: точка Р' совпадает с точкой Р; б) точка Р' принадлежит лучу РА; в) точка Р' принадлежит лучу РВ.
Пусть точка Р' совпадает с точкой Р. Если Q' — точка
луча QC, то 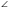 Q'P'B является объединением углов Q'PQ и QPB, по
Q'P'B является объединением углов Q'PQ и QPB, по
этому луч h либо лежит внутри угла Q'P'Q, либо совпадает с лучом PQ, либо лежит внутри угла QPB (рис. 3 а). В первом и во
втором случаях луч h пересекает отрезок Q'Q, поэтому пересекает
и луч Q'Q. В третьем случае луч h по условию теоремы пересекает
луч QD и, следовательно, луч Q'D.
Если Q' — точка луча QD, то угол Q'P'B является частью угла QPB (рис. 3, б). Поэтому луч h является внутренним лучом угла QPB и по условию теоремы пересекает луч QD. Точка пересечения является точкой луча Q'D, так как h не проходит внутри угла QPQ' и поэтому не пересекает отрезок QQ'.
б) Точка Р' принадлежит лучу РА. Луч h лежит
внутри угла Q'P'P, поэтому h пересекает отрезок PQ' в некоторой
точке М (рис. 4). Отложим от луча РВ в полуплоскость, содержащую прямую CD, угол ВРМ', равный углу РР'М. Так как 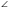 BPQ' —
BPQ' —
внешний угол треугольника PP'Q', то 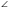 PP'Q' LBPQ', поэтому
PP'Q' LBPQ', поэтому
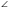 РР'М BPQ'. Отсюда следует, что РМ' — внутренний луч
РР'М BPQ'. Отсюда следует, что РМ' — внутренний луч
угла BPQ'. Следовательно, по доказанному этот
луч пересекает луч Q'D в некоторой точке Mi (рис. 4). Прямая Р'М
пересекает сторону PQ' треугольника PQ'M\ и не пересекает сторону РМ\ (так как  ВРМ1 =
ВРМ1 =  BP'M), поэтому по аксиоме Паша
BP'M), поэтому по аксиоме Паша
прямая Р'М пересекает отрезок Q'М1. Таким образом, луч h пересекает луч Q'D. Чтд.
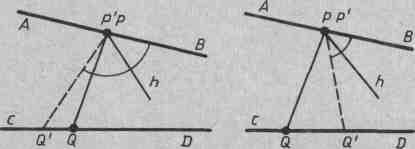
Рис 3 а Рис.3 б
Рис.4
II.3.Теорема о существовании параллельных прямых. Теорема: Пусть АВ — произвольная направленная прямая, а М — точка, не лежащая на ней. Тогда в плоскости МАВ существует одна и только одна прямая CD, проходящая через точку М и параллельная прямой АВ, т. е. CD||AB.
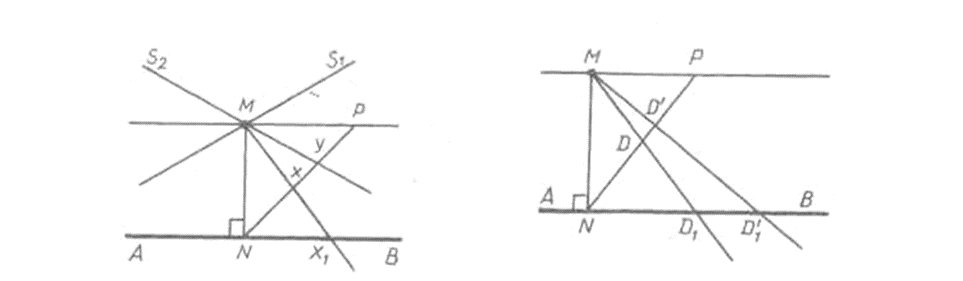
Рис. 5 Рис.6
Рассмотрим перпендикуляр MN, проведенный из точки М к прямой АВ, и прямую MP, перпендикулярную к прямой MN. Мы предполагаем, что точки Р и В лежат по одну сторону от прямой MN. По лемме 1 прямые MP и NB не пересекаются.
Точки отрезка NP разобьем на два класса К1 и К2 по следующему закону: к первому классу отнесем те точки X этого отрезка, которые удовлетворяют условию: луч MX пересекает луч NB, а ко второму классу — все остальные точки отрезка NP. Докажем, что указанное разбиение удовлетворяет условиям а) и б) предложения Дедекинда.
а) Очевидно, N  К1 и Р
К1 и Р  К2. Класс К1 содержит точки, отличные от N, например, точки X пересечения луча МХ1 с отрезком NP, где
К2. Класс К1 содержит точки, отличные от N, например, точки X пересечения луча МХ1 с отрезком NP, где
Х1 — произвольная точка луча NB. Класс K2 содержит
точки, отличные от Р. В самом деле, по аксиоме Лобачевского существует пря
мая MS1, отличная от прямой MP и не пересекающая прямую АВ.
Прямая MS2, симметричная прямой MS1 относительно прямой MN, также не пересекает прямую АВ. Одна из прямых MS1 или MS2 проходит внутри угла NMP, поэтому пересекает отрезок NP в некоторой точке Y, принадлежащей классу К2
б) Пусть X — произвольная точка класса К1, отличная от N, а Y — точка второго класса. Тогда N — X — У, так как в противном случае имеем N — Y — X, что означает, что луч MY — внутренний луч угла NMX. Отсюда следует, что луч MY пересекает отрезок NХ1 т. е. У  К1.
К1.
Итак, на множестве точек отрезка NP имеем дедекиндово сечение. Пусть точка D производит это сечение. Докажем, что D  К2. Предположим противное: D
К2. Предположим противное: D К1 . Тогда луч MD пересекает луч NB в некоторой точке D1 (рис. 6). Возьмем на луче NB точку D’1 так, чтобы N — D1— D’1. Луч MD’1 пересекает отрезок DP в некоторой точке D', которая принадлежит классу K1. Полученный вывод противоречит предложению Дедекинда. Таким образом, D
К1 . Тогда луч MD пересекает луч NB в некоторой точке D1 (рис. 6). Возьмем на луче NB точку D’1 так, чтобы N — D1— D’1. Луч MD’1 пересекает отрезок DP в некоторой точке D', которая принадлежит классу K1. Полученный вывод противоречит предложению Дедекинда. Таким образом, D  К2. На прямой MD возьмем точку С так, чтобы С — М — D. По теореме 1 CD||AB.
К2. На прямой MD возьмем точку С так, чтобы С — М — D. По теореме 1 CD||AB.
Остается доказать, что CD — единственная прямая, проходящая через точку М и параллельная прямой АВ. Пусть, напротив, C’D' — другая прямая, проходящая через точку М и параллельная прямой АВ. По определению параллельных прямых внутренние лучи углов NMD и NMD' пересекают луч NB, поэтому лучи MD, MD' лежат в той же полуплоскости с границей MN, что и луч NB. Отсюда мы приходим к выводу, что, либо MD — внутренний луч угла NMD', либо MD' — внутренний луч угла NMD.
Но тогда одна из прямых
CD или
C'Dr пересекает прямую
АВ, что противоречит определению параллельности прямых.
Рис.7
А N B
3. Пусть М — точка, не лежащая на прямой a, a MN — перпендикуляр, проведенный из точки М на прямую а. Выберем на прямой а две точки А и В так, чтобы А—N — В. Из предыдущей теоремы следует, что через точку М проходит единственная прямая CD, параллельная направленной прямой АВ, и единственная прямая EF, параллельная направленной прямой ВА.
В ходе доказательства теоремы мы установили, что углы DMN и FMN острые, поэтому CD и EF — различные прямые. Докажем, что  DMN =
DMN =  FMN. Пусть, напротив,
FMN. Пусть, напротив,  DMN
DMN 
 FMN, например
FMN, например  DMN
DMN  FMN. Рассмотрим луч MF', симметричный лучу MF относительно прямой MN (луч MF' не изображен на рис. 7). Этот луч является внутренним лучом угла DMN. Так как MF не пересекает прямую АВ, то и MF' не пересекает эту прямую. Но это противоречит определению параллельности прямых CD и АВ.
FMN. Рассмотрим луч MF', симметричный лучу MF относительно прямой MN (луч MF' не изображен на рис. 7). Этот луч является внутренним лучом угла DMN. Так как MF не пересекает прямую АВ, то и MF' не пересекает эту прямую. Но это противоречит определению параллельности прямых CD и АВ.
Таким образом, через каждую точку М, не лежащую на данной прямой а, проходят две прямые, параллельные прямой а, в двух разных направлениях. Эти прямые образуют равные острые утлы с перпендикуляром MN, проведенным из точки М к прямой а. Каждый из этих углов называется углом параллельности в точке М относительно прямой а.
Докажем, что величина угла параллельности вполне определяется расстоянием от точки М до прямой а. На этом рисунке NMD — угол параллельности в точке М относительно прямой a, a N’M’D’ — угол параллельности' в точке М'
относительно прямой а’,  = NMD, x = MN, a/ = N'M'D', x' =M/N/.
= NMD, x = MN, a/ = N'M'D', x' =M/N/.
Докажем, что если х = х’, то  =
=  '. Пусть, напротив,
'. Пусть, напротив,  /
/
 ,
,
например а'  . Тогда существует внутренний луч h’ угла N'M'D',
. Тогда существует внутренний луч h’ угла N'M'D',
такой, что угол между лучами M'N' и h равен  . Луч h’ пересекает
. Луч h’ пересекает
прямую а' в некоторой точке F’. На прямой а от точки N отложим
отрезок NF = N'F’ так, чтобы точки F и D лежали в одной полуплоскости с границей MN. Получим треугольник MNF, равный треугольнику M'N'F'. Так

М
F
рис.8
как NMF = , то лучи MD и MF совпадают. Приходим к выводу, что прямые MD и
, то лучи MD и MF совпадают. Приходим к выводу, что прямые MD и  пересекаются. Это противоречит определению параллельных прямых. Таким образом,
пересекаются. Это противоречит определению параллельных прямых. Таким образом,  =
=  ’.
’.
Итак,  — функция от х:
— функция от х:  = П (х). Она называется функцией Лобачевского и играет существенную роль в гиперболической геометрии. Из предыдущего изложения ясно, что функция П (х) определена для каждого положительного х и что 0 II (х)
= П (х). Она называется функцией Лобачевского и играет существенную роль в гиперболической геометрии. Из предыдущего изложения ясно, что функция П (х) определена для каждого положительного х и что 0 II (х)
Н. И. Лобачевский получил аналитическое выражение этой функции:
,где k — некоторое положительное число.
Из этой формулы следует, что П(х)— монотонно убывающая непрерывная функция. Из этой формулы следует также, что П(х) принимает все значения, лежащие между 0 и П/2 . Другими словами, любой острый угол является углом параллельности в некоторой точке относительно данной прямой.
В геометрии Лобачевского существует зависимость между угловыми и линейными величинами; в этом существенное отличие геометрии Лобачевского от геометрии Евклида.
II.4.Треугольники и четырехугольники на плоскости Лобачевского.
Одними из основных плоских фигур являются треугольник и четырехугольник. Проведем анализ геометрии этих фигур на плоскости Лобачевского.
1. Все теоремы о треугольниках, которые в евклидовой геометрии доказывают без помощи аксиомы параллельности, имеют место также и в геометрии Лобачевского: теоремы о равнобедренных треугольниках, три признака равенства треугольников, теорема о внешнем угле треугольника, теоремы о соотношениях между сторонами и углами, теоремы о пересечении биссектрис внутренних углов треугольника и о пересечении медиан треугольника в одной точке и др. теоремы.
Но треугольники и четырехугольники на плоскости Лобачевского обладают рядом специфических свойств. Рассмотрим некоторые из них.
Теорема 1. Сумма углов любого треугольника меньше 2d.
Пусть ABC— произвольный треугольник. По теореме Саккери — Лежандра (Сумма углов треугольника не больше 2d)  АВС
АВС  2d. Если предположить, что
2d. Если предположить, что  АВС = 2d, то окажется справедливым V постулат, что противоречит аксиоме Лобачевского. Следовательно,
АВС = 2d, то окажется справедливым V постулат, что противоречит аксиоме Лобачевского. Следовательно,  АВС 2d. Ч.т.д.
АВС 2d. Ч.т.д.
Следствие. Сумма углов треугольника непостоянна, т. е. не одна и та же для всех треугольников.
Теорема 2. Сумма углов выпуклого четырехугольника меньше 4 d..
Пусть ABCD —данный выпуклый четырехугольник. Проведем
диагональ АС и разложим этот четырехугольник на два треугольника
ABC и ADC. Тогда А+В+С+D= АВС +
АВС + ADC. Но
ADC. Но  АВС 2d и
АВС 2d и
 ADC 2d, поэтому А + В + С + D d. Ч.т.д.
ADC 2d, поэтому А + В + С + D d. Ч.т.д.
Теорема 3. Если три угла одного треугольника соответственно равны трем углам другого треугольника, то эти треугольники равны.
Пусть в треугольниках ABC и А'В'С' имеем  A =
A =  A’
A’
 B =
B =  B',
B',  C =
C =  С’. Докажем сначала, что АВ = A’В’. Предположим, что АВ
С’. Докажем сначала, что АВ = A’В’. Предположим, что АВ А'В'; для определенности допустим, что АВ А'В'. На лучах АВ и АС возьмем точки В" и С" так, чтобы АВ" = А'В' и АС" = А'С’. По первому признаку равенства треугольников имеем ∆АВ"С" = ∆А'В'С, поэтому
А'В'; для определенности допустим, что АВ А'В'. На лучах АВ и АС возьмем точки В" и С" так, чтобы АВ" = А'В' и АС" = А'С’. По первому признаку равенства треугольников имеем ∆АВ"С" = ∆А'В'С, поэтому  1 =
1 =  2.
2.
По условию  2 =
2 =  3, следовательно,
3, следовательно,  1 =
1 =  3. Аналогично устанавливаем, что
3. Аналогично устанавливаем, что  4 =
4 =  6.
6.
По предположению АВ А’В’ поэтому А — В" — В, т. е. прямая В"С" пересекает сторону АВ треугольника ABC. В силу равенства  1 =
1 =  3 прямые В" С" и ВС не пересекаются, следовательно, по аксиоме Паша прямая В"С" пересекает сторону АС треугольника ABC, и значит, А — С" — С. Отсюда следует, что четырехугольник BB”C”C выпуклый.
3 прямые В" С" и ВС не пересекаются, следовательно, по аксиоме Паша прямая В"С" пересекает сторону АС треугольника ABC, и значит, А — С" — С. Отсюда следует, что четырехугольник BB”C”C выпуклый.
Из равенств  1 =
1 =  3 и
3 и  4 =
4 =  6 следует, что сумма углов этого четырехугольника равна 4d. Таким образом приходим в противоречие с теоремой 2. Значит, АВ = А’B’. По второму признаку равенства треугольников
6 следует, что сумма углов этого четырехугольника равна 4d. Таким образом приходим в противоречие с теоремой 2. Значит, АВ = А’B’. По второму признаку равенства треугольников  АВС =
АВС = A'В'С'. Ч.т.д.
A'В'С'. Ч.т.д.

Выпуклый четырехугольник называется двупрямоугольником, если два угла, прилежащие к одной стороне, прямые. Если ABCD — двупрямоугольник с прямыми углами А и В, то сторона АВ называется основанием, а стороны AD и ВС — боковыми сторонами. Двупрямоугольник с равными боковыми сторонами называется четырехугольником Саккери. Рассмотрим некоторые свойства двупрямоугольников.
1°. Если ABCD — четырехугольник Саккери с основанием АВ, то  С=
С= D и каждый из углов С и D острый.
D и каждый из углов С и D острый.
2°. Если в двупрямоугольнике
ABCD с основанием
АВ AD BC, то  СD.
СD. 3°. Если в двупрямоугольнике ABCD с основанием АВ  С D, то AD
С D, то AD
II.5. Дефект треугольника и многоугольника
Учитывая, что в геометрии Лобачевского сумма углов треугольника меньше 2d, введем понятие о дефекте треугольника, который равен разности между 2d и суммой углов этого треугольника: DABC=2d-SABC.
Нетрудно видеть, что если отрезок BD разделяет АВС на треугольники ABD и DBC, то DABC=DABD+DDBC.
Для n-угольника дефект вводится как разность между 2d(n-2) и суммой его углов. Если многоугольник разбит ломаными на несколько многоугольников, то дефект полного многоугольника равен сумме дефектов его частей.
III.Практическое применение геометрии Лобачевского.
III.1.Теорема Пифагора.
Теорема. Для всякого прямоугольного треугольника плоскости Лобачевского выполняется равенство ch c = ch a ·ch b, где a, b - длины катетов, c - длина гипотенузы этого треугольника, а ch x= (гиперболический косинус).
(гиперболический косинус).
Доказательство.
Воспользуемся моделью Пуанкаре плоскости Лобачевского на евклидовой полуплоскости. Будем считать (см. рисунок ниже), что вершинам A, B, C данного прямоугольного треугольника соответствуют комплексные числа
 где
где 
так как этого всегда можно добиться с помощью некоторого неевклидова движения.
Используя формулу

для вычисления неевклидова расстояния между точками z и w в H2, получаем, что

Почленное перемножение двух первых соотношений и приводит, как показывает третье соотношение, к завершению доказательства теоремы.
1а. Замечание к теореме Пифагора
Н.И.Лобачевским было замечено, что созданная им неевклидова геометрия в бесконечно малом, то есть в первом приближении, совпадает с геометрией евклидовой плоскости. Проиллюстрируем это на примере теоремы Пифагора. Используя разложение гиперболического косинуса в ряд
 получим для теоремы Пифагора соотношение
получим для теоремы Пифагора соотношение

Исключая теперь члены низшего порядка, приходим к теореме Пифагора евклидовой геометрии: 
III.2. Площадь треугольника
Вывод формулы площади треугольника на плоскости Лобачевского сложен, так как в нем используется формулы, доказываемые лишь в курсе дифференциальной геометрии.

Если АВС – треугольник в модели Пуанкре, меры углов А,В и С - α, β и γ соответственно,  - мера угла B в треугольнике ABD, а
- мера угла B в треугольнике ABD, а  и
и  мера углов B и C в треугольнике BCD. Тогда вследствие этого можно сформулировать теорему
мера углов B и C в треугольнике BCD. Тогда вследствие этого можно сформулировать теорему
Теорема. Для площади треугольника ABC с углами справедлива формула
справедлива формула 
Следствие1.Площадь треугольника плоскости Лобачевского ограничена.
Следствие 2.Если дан выпуклый многоугольник  с внутренними углами
с внутренними углами  то
то 
III.3.Применение геометрии Лобачевского в математических науках
Сам Н.И. Лобачевский считал, что для выполнения расчетов, связанных с геометрическими свойствами и измерениями в пределах Солнечной системы, будет достаточно евклидовой геометрии. Однако геометрия Лобачевского используется внутри математики, в математическом анализе при отыскании значений интегралов. А.Пуанкаре применил геометрию Лобачевского при построении и развитии автоморфных функций. Но действенность геометрии Лобачевского пришлась на XX век, когда А.А.Фридман открыл приложение к геометрии Лобачевского, которое назвали «пространством Фридмана-Лобачевского».
В наши дни геометрия Лобачевского используется в космонавтике для прокладывания дальних маршрутов, вычисления траектории полета, в современной физике и во многих других естественных науках.
Геометрия Лобачевского и, открытая за нею неевклидова геометрия Римана, прочно вошли в современную науку, геометрия Евклида сохраняет свое полное значение в вопросах практики, строительства и техники. Неевклидовы геометрии находят себе применение в некоторых более сложных теоретических и практических вопросах современной математики, физики и технике.
Лобачевский указывал на связь геометрии с физикой, и хотя его измерения углов треугольника с громадными астрономическими размерами показали еще справедливость евклидовой геометрии, на самом деле, как оказалось позже, поправки, полученные в рамках теории, основанной именно на неевклидовой геометрии, оказались заметными даже внутри планетной системы, объяснив знаменитую аномалию движения Меркурия, обнаруженную в XIX столетии Леверье.
Предположение Лобачевского, что реальные геометрические отношения зависят от физической структуры материи, нашло подтверждение не только в космических масштабах. Современная теория квант все с большей настоятельностью выдвигает необходимость применения геометрии, отличной от евклидовой, к проблемам микромира.
К сожалению, ученые долго не уделяли должного внимание данной геометрии, видимо потому, что не изучали ее. Поэтому, у меня возник вопрос: «Каким образом знакомят учащихся образовательных школ с Лобачевским и его геометрией?»
III.4.Анализ состава исторической справки о Н.И. Лобачевском в школьном курсе математики
Для анализа состава исторической справки о Н.И. Лобачевском было рассмотрено три учебника геометрии для общеобразовательной школы для учащихся 7 − 9 классов под редакциями Л.С. Атанасяна, А.В. Погорелов, И.Ф. Шарыгина.
В учебнике «Геометрия» для 7-9 классов по ред. Л. С. Атанасяна в §2. п.28 «Аксиома параллельных прямых» о Н.И. Лобачевском упоминается следующее: «огромную роль в решении доказательства пятого постулата сыграл великий русский математик Николай Иванович Лобачевский (1792-1856)».
В учебнике «Геометрия» для 7-9 классов под ред. А. В. Погорелова в п. 37 «Из истории возникновения геометрии» говорится, что «…Аксиома параллельных в отличие от других аксиом не подкрепляется наглядными соображениями. Может быть, поэтому со времен Евклида математики многих стран пытались доказать ее как теорему. Но это никому не удавалось. Наконец, в XIX в. было доказано, что это невозможно сделать. Первым, кто обоснованно высказал это утверждение, был великий русский математик Николай Иванович Лобачевский».
В учебнике «Геометрия» для 7-9 классов под ред. И.Ф. Шарыгина в §5 «Параллельные прямые и углы» выделяется отдельный подпункт с названием «Лобачевский и история открытия неевклидовой геометрии»
В учебнике «Алгебра» 9 класс под ред. Ю.Н Макарычева и др. в главе I «Квадратичная функция» есть краткая история о Н. И. Лобачевском (1792-1856), в котором говорится, что он русский математик, создатель неевклидовой геометрии, которая изменила представлении о роли аксиоматики в математики и сыграла важную роль в разработке теории относительности. Большой вклад он внес также в математический анализ и алгебру, разработал метод приближенного решения алгебраических уравнений высших степеней.
В других учебниках (Алгебра 9 кл. под ред. А.Г. Мордковича и др.; Алгебра под ред. С.М. Никольского и др.) нет никакой информации о Н.И. Лобачевском.
Таким образом, можно утверждать, что геометрии Лобачевского в школьном курсе математики уделяется очень мало внимания. В 8-9 классах, в рамках занятий математического кружка, педагоги знакомят учащихся с историей возникновения неевклидовой геометрии, с простыми задачами из геометрии Лобачевского.
IV.Заключение
Открытие Лобачевского всколыхнуло умы ученых, как современников, так и последователей великого ученого. Лобачевский вошел в историю математики не только как гениальный математик, но и как автор фундаментальных работ в области алгебры, теории бесконечных рядов и приближенного решения уравнений, в области теории вероятности, физики, механики, астрономии. Известный английский математик Уильям Клиффорд назвал Лобачевского «Коперником геометрии».
Геометрия Лобачевского помогает по-другому взглянуть на окружающий мир. Мне близко название, которое дал своему открытию сам Николай Иванович – «Воображаемая геометрия». А ведь на самом деле геометрия Лобачевского удивительна и во многом не соответствует представлениям о реальном мире. Но в логическом отношении данная геометрия не уступает геометрии Евклида. Жизнь Николая Ивановича Лобачевского может служить примером того, как добиваться поставленной цели. Даже оставшись в одиночестве, он не отступил, продолжал свои исследования. Геометрия Лобачевского способствовала и способствует более глубокому пониманию окружающего нас материального мира. Изучение космического пространства, исследования в области высоких энергий и многое другое было бы невозможно без применения геометрии Лобачевского.
V.Список использованной литературы
Л.С.Атанасян, В.Т.Базылев. геометрия ч. II . Москва «Просвещение» 1987г.
Атанасян Л. С. Геометрия Лобачевского [Электронный ресурс] /Л. С. Атанасян.—2-е изд., испр. (эл.)2014г..—Электрон –с467
В.Т.Базылев, К.Л.Дуничев. Геометрия ч. II. М: 1975г.
Бокова К. Д., Майоров И. Г., Козлова Д. В., Потапова Н. Ю. Геометрия Лобачевского // Юный ученый. — 2016. — №6.1. — С. 13-15
Васильев А.В. Николай Иванович Лобачевский. - М., 1992. - 229 с.
Г.И. Глейзер. История математики в школе IX – X классы. Пособие для учителей. Москва, «Просвещение» 1983г.
Д.Гильберт. Основания геометрии.- М: ГИТТЛ 1948г
Ефимов Н.В., Высшая геометрия, «Наука», М.,1971г
Каган В.Ф. «Лобачевский и его геометрия», М., 1955- с.303
“Квант” №11, №12 Академик АН СССР А.Д. Александров, Интернет-издания.
Кутузов Б.В. Геометрия Лобачевского и элементы оснований геометрии, М.,1950г., с.129
Лаптев Б.Л. Николай Иванович Лобачевский. - Казань, 1976. - 136 с.
Лаптев Б.Л. Коперник геометрии. - Наука и жизнь, 1976, N5. - С. 38-42.
Лаптев Б.Л. Геометрия Лобачевского, е история и значение. - М.: Знание (В серии "Новое в жизни, науке и технике", N9). 1976. - 36 с.
ЛОБАЧЕВСКИЙ И XXI ВЕК Материалы Международной студенческой конференции, посвященной 210-летию Казанского университета и Дню математики г. Казань, 28 ноября 2014 года с258
Математика. Все для учителя! № 11 (23) ноябрь 2012с.30-33
Математика XIX века, «Наука», М., 1981.
Норден А.П. Великое открытие Лобачевского. "Квант". 1976. N2.
Нут Ю.Ю. «Геометрия Лобачевского в аналитическом изложении»,М.,1961г.-с313
Н.Г.Подаева , Д.А. Жук. Лекции по основам геометрии. Елец: 2008г
Прасолов В.В. Геометрия Лобачевского, МЦМНО, 2004г., с.89
Широков П.А. Краткий очерк основ геометрии Лобачевского. - 2-е изд. - М. Главная редакция физико-математической литературы,1983. – с.80
Электронные ресурсы
http://www.bankreferatov.ru
http://www.refportal.ru
http://festival.1september.ru
https://ru.wikipedia.org/wiki/Геометрия_Лобачевского
http://sernam.ru/book_e_math.php?id=66
http://nsportal.ru/ap/library/nauchno-tekhnicheskoe-tvorchestvo/2014/09/22/referat-po-matematike-na-temu-geometriya
Приложение
1. Задачи.
1. Сможет ли самолёт оказаться в той же точке, если пролетит 1 км. на юг, 1 км. на восток и 1 км. на север?
Ответ: сможет, если он вылетит с севера.
2. В сферической геометрии окружность максимального радиуса называется «прямой» линией.
Дано:
сфера(R;О),
две прямые на сфере
Доказать:
любые прямые пересекаются
Доказательство:
Вторая «прямая» полностью лежит в одной из полусфер, потому что первая «прямая» делит сферу на две половины.
Поэтому её радиус (r) вторая «прямая» не является прямой = любые две «прямые» пересекаются на сфере, что и требовалось доказать.
Задача 3.
Дано
сфера(R;О),
угол α =45°
ΔABC
Найти:
Сумму углов ΔABC, образованного двумя меридианами и параллелью.
Решение:
AC перпендикулярна DF; AB перпендикулярна DF ( как меридианы) = угол β и угол α = 90° =
ΔABC = угол α + угол β + угол 1 = (90°·2) + 45°= 225°.
Ответ:225о
Ниже приведены иллюстрации к задачам:
Задача 4.
Дано:
сфера(R;О),
сфера разбита на 8 частей (равных) тремя ортогональными прямыми; каждая часть является сферическим треугольником.
Найти:
Сумму углов ABC.
Решение:
Так как стороны треугольника ортогональны, углы треугольника по 90° = сумма углов ΔABC = 90°· 3 = 270°.
Ответ: 270°.







 «Оренбургский государственный педагогический университет»
«Оренбургский государственный педагогический университет» Рис. 1
Рис. 1 Рис. 2
Рис. 2 Рис. 3
Рис. 3
 Рис.4
Рис.4
 АВ и Q
АВ и Q 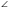 Q'P'B является объединением углов Q'PQ и QPB, по
Q'P'B является объединением углов Q'PQ и QPB, по ВРМ1 =
ВРМ1 = 


 К1 и Р
К1 и Р  К1 . Тогда луч MD пересекает луч NB в некоторой точке D1 (рис. 6). Возьмем на луче NB точку D’1 так, чтобы N — D1— D’1. Луч MD’1 пересекает отрезок DP в некоторой точке D', которая принадлежит классу K1. Полученный вывод противоречит предложению Дедекинда. Таким образом, D
К1 . Тогда луч MD пересекает луч NB в некоторой точке D1 (рис. 6). Возьмем на луче NB точку D’1 так, чтобы N — D1— D’1. Луч MD’1 пересекает отрезок DP в некоторой точке D', которая принадлежит классу K1. Полученный вывод противоречит предложению Дедекинда. Таким образом, D 

















