УО «Полесский государственный аграрный колледж имени В.Ф. Мицкевича»
Материалы для самостоятельной работы учащихся
по дисциплине «Математика».
Тема
«Логарифм числа.
Логарифмическая функция.
Решение логарифмических уравнений
и неравенств»

г. Калинковичи
Краткие теоретические сведения
Логарифмом числа b по основанию а называется показатель степени, в которую нужно возвести основание а, чтобы получить число b.
Основное логарифмическое тождество

Логарифм по основанию 10 имеет специальное обозначение 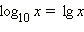 и называется десятичным логарифмом. Для десятичных логарифмов справедливы равенства:
и называется десятичным логарифмом. Для десятичных логарифмов справедливы равенства:
| lg 1 = 0 | lg 0,1 = –1 |
| lg 10 = 1 | lg 0,01 = –2 |
| lg 100 = 2 | lg 0,001 = –3 |
| lg 1000 = 3 | lg 0,0001 = –4 |
Логарифм по основанию e имеет в математике большое значение. Число e приблизительно равно 2,7. Более точное выражение:
однако само число e является иррациональным. Для логарифма по этому основанию также существует специальное обозначение  и название натуральный логарифм. Среди свойств числа e, в частности, можно отметить следующее: касательная к графику функции
и название натуральный логарифм. Среди свойств числа e, в частности, можно отметить следующее: касательная к графику функции  в точке (0; 1) образует с осью абсцисс угол 45°.
в точке (0; 1) образует с осью абсцисс угол 45°.
Основные свойства логарифмов
При любом а 0 (а≠1) и любых положительных х и у выполнены равенства:



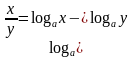






Формула перехода от одного основания логарифма к другому основанию

Десятичный логарифм: 
Натуральный логарифм:  где e = 2,71828
где e = 2,71828
Логарифмическая функция
Функцию, заданную формулой  называют логарифмической функцией с основанием а.
называют логарифмической функцией с основанием а.
Свойства логарифмической функции:
Область определения – множество всех положительных чисел
Область значений – множество всех действительных чисел
При а 1 логарифмическая функция на всей области определения возрастает.
При 0
убывает
Графики логарифмической функции


Решение логарифмических
уравнений и неравенств
Рассмотрим простейшее логарифмическая уравнение 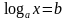 . Логарифмическая функция возрастает ( или убывает) на промежутке (0; ∞) и принимает на этом промежутке все действительные значения. По теореме о корне отсюда следует, что для любого b данное уравнение имеет и при том только одно решение. Из определения логарифма числа сразу следует, что
. Логарифмическая функция возрастает ( или убывает) на промежутке (0; ∞) и принимает на этом промежутке все действительные значения. По теореме о корне отсюда следует, что для любого b данное уравнение имеет и при том только одно решение. Из определения логарифма числа сразу следует, что  является решением уравнения.
является решением уравнения.
Методы решения логарифмических уравнений
, a 0, a ≠ 1
 , a 0, a ≠ 1
, a 0, a ≠ 1 
Для перехода к простейшим уравнениям используются методы разложения на множители, замены переменных, переход к одному основанию, функциональные и оценочные методы.
Методы решения логарифмических неравенств
Полезные соотношения
Образцы решений
Пример 1
Вычислите 1)  2)
2)  3)
3) 
Решение
| 1)  так как так как  2)  так как так как  3) Ответ. 1)  2) 4; 3) 2) 4; 3)  |
Пример 2
Вычислите 1) ; 2)
; 2)  .
.
Решение
| 1)  так как так как  2) Ответ. 1) −3; 2) −3. |
Пример 3
Вычислите 1)  2)
2) 
Решение
| 1) 2) Ответ. 1) 5; 2) 2401. |
Пример 4
Вычислите  если
если 
Решение
| Перейдём в log6 5 к основанию 2. Имеем Однако по условию:  Аналогично Аналогично  Значит, Значит, Ответ.  |
Уравнения вида loga f (x) = b, a 0, a ≠ 1
Здесь предполагается, что f (x) − функция, уравнения с которой мы уже умеем решать. По определению логарифма из основного логарифмического тождества получаем, что f (x) = ab. Это уравнение можно решать любыми доступными методами, поскольку ab – это число.
Уравнения вида 
Совершенно аналогично показательным уравнениям, уравнения такого типа решаются в два этапа.
Понятно, что совершенно не обязательно уравнение будет иметь рассмотренный вид. А значит, в процессе преобразований логарифмических уравнений следует стремиться к тому, чтобы привести все входящие в уравнение логарифмы к одному основанию. При этом необходимо помнить об области определения рассматриваемых выражений, стараясь, чтобы при преобразовании она не уменьшалась, − те корни, которые, возможно, будут приобретены, можно будет отсеять проверкой.
Пример 5
Решите уравнение
Решение
Преобразуем левую часть уравнения, приводя все логарифмы к основанию 7.
а)
Корень последнего уравнения с учётом ограничения x 1 есть x = 3.
б)
Поскольку мы использовали, вообще говоря, неравносильное преобразование суммы логарифмов в логарифм произведения (это расширяет область определения), то необходима проверка, которая показывает, что все три найденных числа являются корнями исходного уравнения. Заметим, что число x = 1 рассматривать не нужно, поскольку оно не входит в ОДЗ уравнения.
Ответ. 0, 3, −7.
Пример 6
Решите уравнение
Решение
| ОДЗ данного уравнения:  Выполним цепочку преобразований, равносильных в ОДЗ. Выполним цепочку преобразований, равносильных в ОДЗ. 1) 3x – 4 = 0,  − входит в ОДЗ. − входит в ОДЗ. 2) (x + 1 0 в ОДЗ), x = 0 − не входит в ОДЗ. x = 3 − входит в ОДЗ. Ответ. 3,  |
Уравнения вида loga f (x) = loga g (x), a 0, a ≠ 1
ОДЗ данного уравнения:  В силу монотонности логарифмической функции, каждое своё значение она принимает ровно один раз. Следовательно, в ОДЗ имеем:
В силу монотонности логарифмической функции, каждое своё значение она принимает ровно один раз. Следовательно, в ОДЗ имеем:
Полная система равносильности выглядит так:
Из двух последних систем выбирается та, которая проще (это зависит от конкретного вида функций f (x) и g (x)). На практике, как правило, проще решить уравнение f (x) = g (x) и проверить для его корней положительность одной из функций: f (x) 0 или g (x) 0, так как из равенства одной из этих функций следует положительность и другой.
Рассмотренный переход от уравнения loga f (x) = loga g (x) к уравнению f (x) = g (x) называется потенцированием.
Заметим, что потенцирование не является равносильным преобразованием. Область определения уравнения при потенцировании расширяется, так как второе уравнение определено при всех x, для которых определены функции f (x) и g (x), а первое − только при тех x, для которых f (x) 0 и g (x) 0.
Пример 7
Решите уравнение 
Решение
| Преобразуем сумму логарифмов в логарифм произведения:  или или  Потенцируя по основанию 10, имеем Потенцируя по основанию 10, имеем  откуда x = –8, x = –10. Подстановка этих чисел в исходное уравнение даёт, что только x = –10 является корнем. откуда x = –8, x = –10. Подстановка этих чисел в исходное уравнение даёт, что только x = –10 является корнем. Ответ. x = –10. |
Пример 8
Решите уравнение
Решение
| Очевидна замена 6 sin x + 4 = t 0 (это требование взято из ОДЗ, ведь от t берётся логарифм). Перейдём к равносильному уравнению: Ответ.  |
Рассмотрим теперь неравенство  и найдём соответствующие ему условия равносильности. ОДЗ этого неравенства: f (x) 0.
и найдём соответствующие ему условия равносильности. ОДЗ этого неравенства: f (x) 0.
Если a 1, то  тогда и только тогда, когда f (x) 1 в ОДЗ (f (x)
тогда и только тогда, когда f (x) 1 в ОДЗ (f (x)
Если 0 a тогда и только тогда, когда f (x) f (x) 1), то есть опять 
Верно и обратное, если  то при a 1 имеем f (x) 1 в ОДЗ (f (x) a f (x) f (x) 1). Таким образом, получаем следующие условия равносильности.
то при a 1 имеем f (x) 1 в ОДЗ (f (x) a f (x) f (x) 1). Таким образом, получаем следующие условия равносильности.
Отсюда следует, что:
| Знак  совпадает со знаком выражения совпадает со знаком выражения  в ОДЗ (f (x) 0). в ОДЗ (f (x) 0). 
|
Рассмотрим теперь неравенство вида  где
где  ОДЗ этого неравенства:
ОДЗ этого неравенства: 
Перепишем данное неравенство в виде:
С учетом ОДЗ можно записать соответствующую неравенству систему уравнений:
Пример 9
Решите неравенство
Решение
| Преобразуем неравенство. От выражений вида  перейдём к произведениям перейдём к произведениям  которые имеют с ними тот же знак в ОДЗ. которые имеют с ними тот же знак в ОДЗ. Пользуясь методом интервалов, легко получить: Ответ. |
Пример 10
Решите неравенство
Решение
| Перейдём во всех логарифмах к основанию 2. Переходя к равносильной системе, заменим разность логарифмов в фигурных скобках на выражение, которое имеет с ним тот же знак в ОДЗ. Кроме того, заменим логарифм, стоящий до фигурной скобки, на выражение, с которым он совпадает по знаку в ОДЗ. Так как в ОДЗ  выполнено неравенство выполнено неравенство  то то С учётом сделанного замечания, последняя система в ОДЗ равносильна следующему уравнению: Так как в ОДЗ x 0, то знак выражения  совпадает со знаком функции совпадает со знаком функции  Нанесем решения всех неравенств на числовую прямую и найдем пересечение полученных областей с ОДЗ. Получим: Ответ.  |
Варианты заданий по уровням
Уровень 1
Решите уравнения и неравенства




















Уровень 2
Решите уравнения и неравенства











Уровень 3
Решите уравнения и неравенства


Уровень 4
Решите уравнения и неравенства

Уровень 5
Решите уравнения и неравенства














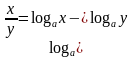








 где e = 2,71828
где e = 2,71828 называют логарифмической функцией с основанием а.
называют логарифмической функцией с основанием а.

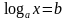 . Логарифмическая функция возрастает ( или убывает) на промежутке (0; ∞) и принимает на этом промежутке все действительные значения. По теореме о корне отсюда следует, что для любого b данное уравнение имеет и при том только одно решение. Из определения логарифма числа сразу следует, что
. Логарифмическая функция возрастает ( или убывает) на промежутке (0; ∞) и принимает на этом промежутке все действительные значения. По теореме о корне отсюда следует, что для любого b данное уравнение имеет и при том только одно решение. Из определения логарифма числа сразу следует, что 


















