Методические рекомендации по изучению темы «Правильные многогранники»

Занятие 99. Тема «Правильные многогранники»

План занятия:

1. Понятие правильного многогранника.

2. Виды правильных многогранников.

3. Полуправильные многогранники.

   1. Понятие правильного многогранника.

Выпуклый многогранник называется правильным, если:

1. все его грани — равные правильные многоугольники;

2. в каждой его вершине сходится одно и то же число рёбер.

Все рёбра правильного многогранника равны, а также равны все двугранные углы, содержащие две грани с общим ребром.

 Возникают вопросы:

1. какие правильные многоугольники могут быть гранями правильного многогранника?

2. Сколько граней может иметь правильный многогранник?

Не существует правильного многогранника, гранями которого являются правильные многоугольники, если число их сторон 6 или больше, то есть правильные n-угольники, если n≥6.

1. У правильного n-угольника, если n≥6, углы не меньше 120°.

2. В каждой вершине многогранника должно быть не меньше трёх углов.

3. Даже при трёх углах сумма всех углов уже достигает 360°.

4. Сумма всех плоских углов при каждой вершине выпуклого многогранника меньше 360°.

Следовательно, не существует правильного многогранника, гранями которого являлись бы правильные n-угольники, если n≥6.

Только правильные треугольники, четырёхугольники (квадраты) и пятиугольники могут быть гранями правильного многогранника.

Существуют ли правильные многогранники с такими гранями, и сколько граней они имеют? Очевидно, меньшее возможное число граней — четыре.

Теорема Эйлера и правильные многогранники

Теорема Эйлера

В любом выпуклом многограннике сумма числа граней и числа вершин на 2 больше числа рёбер.

С помощью теоремы Эйлера мы можем получить ответ на вопрос:

какие правильные многогранники могут существовать?

1. Пусть количество рёбер правильного многогранника, выходящих из одной вершины, равно m, а гранями являются правильные n-угольники.

2. Выразим входящие в формулу Эйлера величины В (вершины) и Г (грани) через:

Р (рёбра), m, n, где n и m — целые числа, и m≥3, n= 3, 4 или 5.

3. Так как каждое ребро соединяет две вершины, и в каждой вершине сходятся m рёбер, то 2Р=Вm.

Тогда В=2Рm.

4. Так как каждое ребро многогранника содержится в двух гранях, то Гn=2Р.

Тогда Г=2Рn.

5. Подставляя полученные выражения для Г и В в формулу Эйлера Г+В−Р=2, получаем

2Рm+2Рn−Р=2.

6. Поделив обе части равенства на 2Р, получим

1m+1n−12=1Р.

7. Решим это уравнение при полученном в предыдущем доказательстве значении n= 3 и найдём допустимые значения m.

 1m+13−12=1Р; 

1m−16=1Р.

По смыслу Р0, значит, 3≤m≤5.

Таким образом, теорема Эйлера разрешает существование следующих правильных многогранников:

1. m=3,n=3,P=6,Г=4 — тетраэдр;
2. m=3,n=4,P=12,Г=6 — куб;

3. m=3,n=5,P=30,Г=12 — додекаэдр;
4. m=4,n=3,P=12,Г=8 — октаэдр;
5. m=5,n=3,P=30,Г=20 — икосаэдр.

Доказано существование правильных многогранников:

тетраэдр с 4 гранями, 6 рёбрами и 4 вершинами:

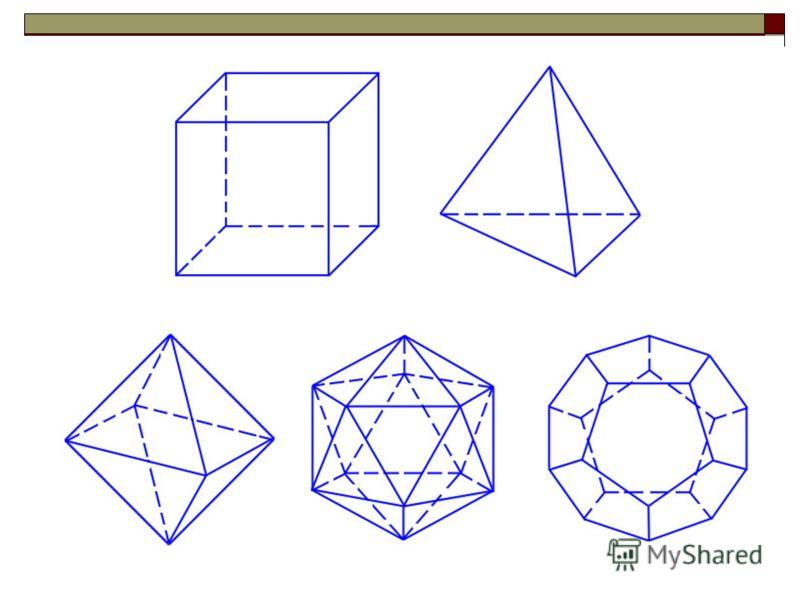
куб с 6 гранями, 12 рёбрами и 8 вершинами:

октаэдр с 8 гранями, 12 рёбрами и 6 вершинами:

додекаэдр с 12 гранями, 30 рёбрами и 20 вершинами:

икосаэдр с 20 гранями, 30 рёбрами и 12 вершинами:

(Для знакомства, можно не конспектировать)

Полуправильные многогранники — в общем случае это различные выпуклые многогранники, которые, не являясь правильными, имеют некоторые их признаки, например: все грани равны, или все грани являются правильными многоугольниками, или имеются определённые пространственные симметрии. Определение может варьироваться и включать различные типы многогранников, но в первую очередь сюда относятся архимедовы тела.

Архимедовы тела — выпуклые многогранники, обладающие двумя свойствами:

• Все грани являются правильными многоугольниками двух или более типов (если все грани — правильные многоугольники одного типа, это — правильный многогранник, или платоново тело);

• для любой пары вершин существует симметрия многогранника (то есть движение, переводящее многогранник в себя), переводящая одну вершину в другую. В частности,

  • все многогранные углы при вершинах конгруэнтны.

Первое построение полуправильных многогранников приписывается Архимеду, хотя соответствующие работы утеряны.

Задание для самостоятельного выполнения

Задание 1. Сделать краткий конспект по данной теме.

Задание 2. Выучить все формулировки определений и теорем.

Задание 3. Изготовить 3 модели: призмы (любой) или пирамиды (любой), и 2 правильных многогранника (один простой куб или тетраэдр или октаэдр и один сложный додекаэдр или икосаэдр). Техника выполнения и материал любой. Самый простой вариант бумажный, для удобства можно воспользоваться готовыми развертками с сайта https://mnogogranniki.ru/.

Выполненные задания и вопросы по выполнению работ отправить на адрес электронной почты преподавателя: [email protected]. Имя файла – фамилия студента и номер занятия. (например, Петров-99)