Обобщенный метод интервалов.
Некоторые алгебраические неравенства степеней более высоких, чем вторая, цепочкой равносильных переходов приводятся к виду

(или 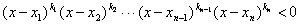 ), (2)
), (2)
где klt k2, ..., kn-1,kn — фиксированные натуральные числа,
х1, х2, … хn-1,xn—фиксированные действительные числа, среди которых нет равных, и такие, что х1<х2< … <хn-1<xn . Тогда неравенства вида (2) решаются так называемым обобщенным методом интервалов.
Рассмотрим многочлен Р(х)=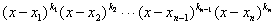 (3)
(3)
Очевидно, что для любого числа yо, такого, что yо> хn, соответствующее значение любого сомножителя в произведении (3) положительно, поэтому числовое значение Р(yо) многочлена Р(х) также положительно.
Для любого числа y1, взятого из промежутка (xn-1,xn) , соответствующее числовое значение любого сомножителя, кроме последнего, положительно; соответствующее числовое значение последнего сомножителя положительно, если kn - четное число, и отрицательно, если kn - нечетное число. Поэтому число Р(y1) - положительно, если kn -четное число, и число Р(y1) - отрицательно, если kn - нечетное число. Обычно в этих случаях говорят, что многочлен Р(х) при переходе через точку xn меняет знак, если kn - нечетное число, и не меняет знака, если kn - четное число.
Аналогично показывается, что если известен знак многочлена Р(х) на промежутке (xi,xi+1), тона промежутке (хi-1,xi), знак определяется по правилу: многочлен Р(х) при переходе через точку xi меняет знак, если kt -нечетное число, и не меняет знака, если kt -четное число. На этом рассуждении и основан обобщенный метод интервалов.
Алгоритм обобщенного метода интервалов
- на числовую ось наносятся числа х1, х2, … хn-1,xn ;
- в промежутке справа от наибольшего из этих чисел, т. е. справа от хn, ставят знак плюс, в следующем за ним справа налево промежутке ставят знак плюс, если kn - четное число, и знак минус, если kn- нечетное число;
- в следующем за ним справа налево промежутке ставят знак, пользуясь правилом: многочлен Р(х) при переходе через точку хn-1 , меняет знак, если kn-1 - нечетное число, и не меняет знака, если kn-l — четное число;
- затем рассматривается следующий за ним справа налево промежуток, в нем ставят знак, пользуясь тем же правилом;
- таким образом рассматриваются все промежутки.
- решением неравенства (2) будет объединение всех промежутков, в которых поставлен знак плюс (или минус).
Решение неравенства  (4)
(4)
в случае, если Р(x), R(x) и M(x) будут многочленами, можно провести так.
Неравенство (4) надо сначала переписать в равносильном виде
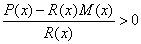 ,
, (4.1)
(4.1)
Затем, воспользовавшись одним из утверждений равносильности неравенств, умножить неравенство (4.1) на R2(х) и записать неравенство
 ,
, ), (5)
), (5)
равносильное неравенству (4.1) на его ОДЗ. Наконец, неравенство (5) решить методом интервалов. Множество всех решений неравенства (5) и будет множеством всех решений неравенства (4).
Пример. Решить неравенство
 (6)
(6)
Прежде всего, умножая это неравенство на 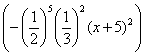 , получим равносильное ему неравенство
, получим равносильное ему неравенство  . (7)
. (7)
Для решения этого неравенства применим обобщенный метод интервалов. На числовой
оси отметим числа (-5),  ,
,  , 7.
, 7. 
Справа от наибольшего числа, т. е. от числа 7, ставим знак плюс. При переходе через точку (7) многочлен 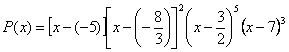 меняет знак, так как двучлен (х-7) содержится в произведении в нечетной степени, поэтому в промежутке
меняет знак, так как двучлен (х-7) содержится в произведении в нечетной степени, поэтому в промежутке  ставим знак минус. При переходе через точку
ставим знак минус. При переходе через точку  многочлен Р(х) меняет знак, так как двучлен
многочлен Р(х) меняет знак, так как двучлен  содержится в произведении в нечетной степени, поэтому в промежутке
содержится в произведении в нечетной степени, поэтому в промежутке 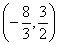 ставим знак плюс. При переходе через точку
ставим знак плюс. При переходе через точку  многочлен Р(х) неменяет знака, так как двучлен
многочлен Р(х) неменяет знака, так как двучлен  содержится в произведении в четной степени, поэтому в промежутке
содержится в произведении в четной степени, поэтому в промежутке 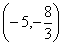 ставим знак плюс. Наконец, при переходе через точку (-5) многочлен Р(х) меняет знак, так как двучлен
ставим знак плюс. Наконец, при переходе через точку (-5) многочлен Р(х) меняет знак, так как двучлен 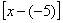 содержится в произведении в первой степени, поэтому в промежутке
содержится в произведении в первой степени, поэтому в промежутке 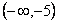 ставим знак минус. Итак, решение неравенства (7) и равносильного ему неравенства (6) - совокупность всех промежутков, где поставлен знак плюс, т. е. множество всех решений неравенства есть множество
ставим знак минус. Итак, решение неравенства (7) и равносильного ему неравенства (6) - совокупность всех промежутков, где поставлен знак плюс, т. е. множество всех решений неравенства есть множество 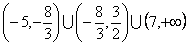 .
.
Суть метода интервалов заключается в следующем:
- С помощью равносильных преобразований приводим неравенство к виду
f(x)*0
где * - один из знаков: >, <, >=, <=.
Комментарий: Выражение f(x) рассматриваем как некоторую функцию и тогда неравенство сводится к нахождению промежутков знакопостоянства и нулей функции.
- Находим нули функции, то есть решения уравнения f(x)=0.








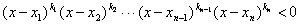 ), (2)
), (2)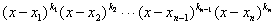 (3)
(3) (4)
(4)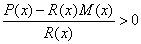 ,
, (4.1)
(4.1) ,
, ), (5)
), (5) (6)
(6)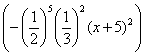 , получим равносильное ему неравенство
, получим равносильное ему неравенство  . (7)
. (7) ,
,  , 7.
, 7. 
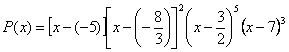 меняет знак, так как двучлен (х-7) содержится в произведении в нечетной степени, поэтому в промежутке
меняет знак, так как двучлен (х-7) содержится в произведении в нечетной степени, поэтому в промежутке  ставим знак минус. При переходе через точку
ставим знак минус. При переходе через точку  многочлен Р(х) меняет знак, так как двучлен
многочлен Р(х) меняет знак, так как двучлен  содержится в произведении в нечетной степени, поэтому в промежутке
содержится в произведении в нечетной степени, поэтому в промежутке 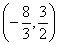 ставим знак плюс. При переходе через точку
ставим знак плюс. При переходе через точку  многочлен Р(х) неменяет знака, так как двучлен
многочлен Р(х) неменяет знака, так как двучлен  содержится в произведении в четной степени, поэтому в промежутке
содержится в произведении в четной степени, поэтому в промежутке 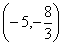 ставим знак плюс. Наконец, при переходе через точку (-5) многочлен Р(х) меняет знак, так как двучлен
ставим знак плюс. Наконец, при переходе через точку (-5) многочлен Р(х) меняет знак, так как двучлен 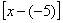 содержится в произведении в первой степени, поэтому в промежутке
содержится в произведении в первой степени, поэтому в промежутке 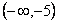 ставим знак минус. Итак, решение неравенства (7) и равносильного ему неравенства (6) - совокупность всех промежутков, где поставлен знак плюс, т. е. множество всех решений неравенства есть множество
ставим знак минус. Итак, решение неравенства (7) и равносильного ему неравенства (6) - совокупность всех промежутков, где поставлен знак плюс, т. е. множество всех решений неравенства есть множество 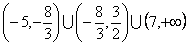 .
.

















