Федеральное агентство по образованию
ФГОУ СПО «Мичуринский аграрный колледж»
Рассмотрено
на заседании цикловой комиссии
общеобразовательных дисциплин
Протокол № ______от _______________
Председатель ___________ И.М. Долгова
Исследовательская работа
Предупреждение и устранение ошибок
при изучении тригонометрических функций
Автор работы:
Долгова И.М.
преподаватель математики и физики
Мичуринск
Оглавление
Введение………………………………………………………………………………………….3
Методика проведения исследований…………………………………………………………...5
Характеристика объекта исследования………………………………………………………...5
Порядок исследований…………………………………………………………………………..6
Заключение……………………………………………………………………………………...14
Библиографический список……………………………………………………………………15
Введение
В древности тригонометрия возникла в связи с потребностями астрономии, землемерия и строительного дела, то есть носила чисто геометрический характер и представляла главным образом «исчисление хорд». Со временем в нее начали вкрапляться некоторые аналитические моменты. В первой половине 18-го века произошел резкий перелом, после чего тригонометрия приняла новое направление и сместилась в сторону математического анализа. Именно в это время тригонометрические зависимости стали рассматриваться как функции. Это имеет не только математико-исторический, но и методико-педагогический интерес.
В настоящее время изучению тригонометрических функций именно как функций числового аргумента уделяется большое внимание в базовом курсе математики ССУЗов. Существует несколько различных подходов к преподаванию данной темы, и преподаватель, особенно начинающий, легко может запутаться в том, какой подход является наиболее подходящим. А ведь тригонометрические функции представляют собой наиболее удобное и наглядное средство для изучения всех свойств функций (до применения производной), а в особенности такого свойства многих природных процессов как периодичность. Поэтому их изучению следует уделить пристальное внимание. Все выше сказанное и обусловливает актуальность выбора темы для данной исследовательской работы.
Кроме того, большие трудности при изучении темы «Тригонометрические функции» возникают из-за несоответствия между достаточно большим объемом содержания и относительно небольшим количеством часов, выделенным на изучение данной темы. Таким образом, проблема этой исследовательской работы состоит в необходимости устранения этого несоответствия за счет тщательного отбора содержания и разработки методов изложения данного материала. Объектом исследования является процесс изучения функциональной линии в базовом курсе математики. Предмет исследования – предупреждение и устранение ошибок при изучении тригонометрических функций.
Таким образом, основной целью написания данной работы является разработка общих методических положений, на которые нужно обратить внимание при изложении темы «Тригонометрические функции».
Гипотеза: изучение тригонометрических функций будет более эффективным в том случае, когда:
1) перед введением тригонометрических функций проведена достаточно широкая пропедевтическая работа с числовой окружностью, которая рассматривается не только как самостоятельный объект, но и как элемент декартовой системы координат;
2) построение графиков осуществляется после исследования свойств тригонометрических функций, исходя из анализа поведения функции на числовой окружности;
3) каждое свойство функции четко обосновано, и все они сведены в систему;
4) твердое знание всех формул, как в прямом, так и в обратном порядке.
Для решения проблемы исследования, проверки достоверности гипотезы и достижения цели реализуются следующие задачи:
- исследование уже имеющейся научно-методической литературы по этой теме;
- экспериментальная проверка эффективности использования разработанной методики.
Для достижения целей работы, проверки гипотезы и решения вышепоставленных задач были использованы следующие методы: наблюдение, анализ, сравнение, опытное преподавание.
Материалы данной исследовательской работы имеют практическую значимость и могут быть использованы преподавателями математики при изложении темы «Тригонометрические функции».
Методика проведения исследований
Исследования проводились в течение двух лет, 2007-2008, 2008-2009 уч. г., методами наблюдения, анализа, сравнения и опытного преподавания. В ходе исследования устанавливаются и систематизируются типичные ошибки, допускаемые студентами при изучении темы «Тригонометрические функции». На основе полученных данных делаются выводы об эффективности предложенной автором методики предупреждения и устранения ошибок при изучении тригонометрических функций.
Характеристика объекта исследования
Во введении говорилось о необходимости изучения тригонометрических функций числового аргумента в базовом курсе математики. Что же обусловливает данную необходимость?
Итак, основными целями изучения тригонометрических функций числового аргумента являются:
1) ознакомление студентов с новым видом трансцендентных функций;
2) развитие навыков вычислительной практики (работа с трансцендентными функциями зачастую требует громоздких вычислений);
3) наглядная иллюстрация всех основных свойств функции (в особенности периодичности);
4) установление межпредметных связей с практикой (изучение колебаний маятника, электрического тока, волновой теории света невозможны без знаний о тригонометрических функциях);
5) развитие логического мышления (обилие формул порождает необходимость преобразований неалгебраического характера, которые носят исследовательский характер).
В изучении тригонометрических функций можно выделить следующие этапы:
I. Первое знакомство с тригонометрическими функциями в геометрии.
Значение аргумента рассматривается в промежутке (00; 900). На этом этапе учащиеся узнают, что sin, cos, tg и сtg угла зависят от его градусной меры, знакомятся с табличными значениями и некоторыми формулами приведения.
II. Обобщение понятий sin, cos, tg и сtg для углов (00; 1800). На этом этапе рассматривается взаимосвязь тригонометрических функций и координат точки на плоскости, доказываются теоремы синусов и косинусов, рассматривается вопрос решения треугольников с помощью тригонометрических соотношений.
III. Введение понятий тригонометрических функций числового аргумента.
IV. Систематизация и расширение знаний о тригонометрических функциях числа, рассмотрение графиков функций, проведение исследования, в том числе с помощью производной.
Отмечу, что существует несколько способов определения тригонометрических функций. Их можно разделить на две группы: аналитические и геометрические. К аналитическим способам относят определение функции у = sinх как решения дифференциального уравнения f"(x) - C*f(x) или как сумму степенного ряда sinх = х - х3/3! + х5/5! - … К геометрическим способам относят определение тригонометрических функций на основе проекций и координат радиус-вектора, определение через соотношения сторон прямоугольного треугольника и определения с помощью числовой окружности. Предпочтение отдается геометрическим способам в силу их простоты и наглядности.
Надо заметить, что изучение тригонометрических функций имеет некоторые особенности. Во-первых, до изучения тригонометрических функций рассматривались функции вида у = f(x), где х и у – некоторые действительные числа, здесь же – углу ставится в соответствие число, что является несколько непривычным для студентов. Кроме того, раньше все функции задавались формулами, в которых явным образом был указан порядок действий над значениями аргумента для получения значений функции. Теперь же студенты сталкиваются с функциями, заданными таблично.
Таким образом, изучая тригонометрические функции, студенты лучше начинают разбираться в сущности самого понятия функции. Они начинают осознавать, что функцией может быть зависимость между любыми множествами объектов, даже если они имеют различную природу (лишь бы каждому значению аргумента соответствовало единственное значение функции).
Порядок проведения исследований
Для проведения исследований были выбраны группы первого курса специальностей: «Механизация сельского хозяйства», «Страховое дело». В ходе исследований обращалось внимание на различную математическую подготовку студентов, устанавливались уровень и глубина знаний контингента по теме «Тригонометрические функции», полученных в основной школе.
Изучалась научно-методическая литература по данной теме. Рассматривались различные подходы при изложении тригонометрических функций. Обращалось внимание на методические приемы, используемые учителями-новаторами при изучении тригонометрии в школе.
Описывались все ошибки, допускаемые студентами в ходе решения тригонометрических задач и упражнений, устанавливались среди них доминирующие и типичные. Наблюдения записывались в дневник.
Изучался уровень познавательного интереса студентов к тригонометрическим функциям.
Результаты исследований
При изучении определений тригонометрических функций надо требовать от студентов точного определения функций и формулировки всех формул. Надо, чтобы все студенты, записывая ту или иную формулу, читали ее формулировку литературным языком, тогда им легче будет применять и увидеть ту или другую формулу при тригонометрических преобразованиях и доказательстве тождеств.
В качестве пропедевтической работы для изучения модели числовой окружности желательно рассмотреть геометрические задачи на нахождение длины дуг четверти окружности данного радиуса, ее трети и половины. Обобщая полученные результаты, необходимо подвести учащихся к тому факту, что для дальнейшей работы выгоднее выбирать окружности именно единичного, а не произвольного радиуса.
В процессе работы с числовой окружностью у учащихся должны быть сформированы следующие умения:
- находить на числовой окружности точки, соответствующие заданным числам, выраженным в долях числа и выраженным не в долях числа;
- составлять аналитические записи для дуг числовой окружности;
- определять принадлежность точки какой-либо координатной четверти;
- работать одновременно в двух системах координат – в криволинейной и прямоугольно-декартовой и осуществлять переход от одной системы координат к другой;
- находить координаты точек числовой окружности и отыскивать на числовой окружности точки по заданным координатам.
Для этого целесообразно рассматривать задания следующих типов:
Найти на числовой окружности точки π/2, π/9, 26π/3, -5π/4 …
Найти на числовой окружности точки 1, 2, -7, 4,5, -31…
Определить, каким четвертям принадлежат точки 21π/4, -37π/6, 10π, -95π
Найти декартовы координаты точек, соответствующих числам π/4, -3π/2, 23π/6, -13π/3…
Найти положительные и отрицательные числа, которым соответствуют точки с координатами (1/2; 3/2), (-2/2; 2/2); (3/2; -1/2), (-1,0)…
Нужно еще раз провести связь между числовой окружностью и числовой прямой. Ведь на числовой прямой можно было откладывать не только положительные, но и отрицательные значения, причем сколь угодно большие. На числовой окружности можно делать то же самое, но следует учитывать тот факт, что на прямой соответствие между точками и числами взаимнооднозначное, а на окружности у каждой точки бесконечно много имен, отличающихся друг от друга на 2к, где к є Z.
Это главное отличие учащиеся должны четко понимать и осознавать. Для этого числовую окружность можно сравнить с колесом, а числовую прямую с бесконечной нитью, на которой отмечены точки. Наматывая нитку на колесо, предварительно совместив соответствующие нулевые точки, можно заметить, что точки, отличающиеся на 2, попадут в одно и тоже место на колесе, благодаря тому, что длина числовой окружности единичного радиуса составляет именно 2.
Когда мы научились работать с числовой окружностью как самостоятельным объектом, можно приступать к введению самих тригонометрических функций.
Не стоит забывать, что определения тригонометрических функций с помощью числовой окружности плохо укладываются в сознании ребят по одной простой причине: на первом этапе определения были даны в геометрической трактовке – как отношения сторон прямоугольного треугольника.
Несмотря на то, что мы уже использовали окружность для введения «новых» определений синуса и косинуса на этапе расширения множества значений, принимаемых углом, необходимо еще раз провести взаимосвязь между прямоугольным треугольником и числовой окружностью.
Рассмотрим числовую окружность единичного радиуса, расположенную в прямоугольно декартовых координатах.
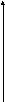 Y
Y


 P
P

 О
О
М X
В положительном направлении от оси ОХ отложим угол такой, что 00. Обозначим полученную на окружности точку как Р. Опустим из точки Р перпендикуляр на ось ОХ, получим точку М. Рассмотрим получившийся прямоугольный треугольник ОМР. Sin по определению равен отношению МР/ОР, но радиус окружности ОР равен единице, следовательно, Sin = МР. Аналогичным образом, cos = ОМ. Заметим, что длина ОМ – это абсцисса точки Р в прямоугольно-декартовой системе координат, а длина МР – ее ордината. Таким образом, синус и косинус угла определяются через ординату и абсциссу точки Р, что является более удобным при работе в прямоугольно-декартовой системе координат.
Сейчас вернемся к наложенным на угол ограничениям. Угол принадлежит промежутку от 00 до 900, а значит и длина дуги лежит между нулем и π/2. Используя все ту же геометрическую интерпретацию, легко показать, что эти определения можно распространить и на любые углы и числа.
Вообще говоря, определив функции синус и косинус, мы уже не нуждаемся в числовой окружности как средстве для введения понятий тангенса и котангенса. Но раз уж мы взялись работать с этой моделью, то неплохо бы показать, как определить функции тангенс и котангенс, используя только их геометрические определения (заметим, что выражения «тангенс угла – это отношение синуса к косинусу» и «котангенс угла – это отношение косинуса к синусу» не являются определениями – это уже свойства).
Чтобы расширить понятие угла удобно рассматривать несколько задач вида:
Задача: на сколько градусов повернется спица велосипеда за 20 секунд, если за 1 секунду она поворачивается на 20 градусов.
Решение: α = 200 * 20 = 400 = 3600 + 400
Ответ: спица велосипеда совершит один полный оборот и повернется еще на 400.
Большое внимание надо обращать на радианную меру угла и переход от радианной меры к градусной и обратно.
Обратить внимание на функции числового аргумента, чтобы студенты могли находить функции числового аргумента по таблицам.
Например: sin2 = 0,9093 и что sin2 . Здесь 2 – значение аргумента и что это угол в радианах, а не отвлеченное понятие.
Некоторые студенты считают, что sin0,7562 = 0,7562. Нужно особо обратить внимание на то, что sin0,7562 ≠ 0,7562.
В тригонометрических преобразованиях студенты стремятся перевести радианную меру угла в градусную (заменить π = 1800 и т.д.). Этого делать не следует, надо, чтобы студенты привыкали работать с радианной мерой угла и умели вести преобразования выражений, в которых встречаются функции угла в радианах, умели пользоваться таблицами: тригонометрические функции аргумента в радианах. При изучении формул приведения требовать от студентов записи формул в градусной и радианной мере.
Например: sin(900 + α) = cosα или sin(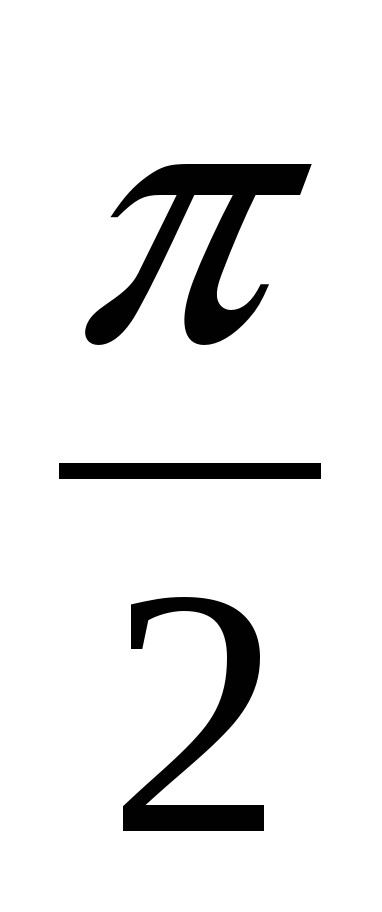 ) + α = cosα.
) + α = cosα.
Остановлюсь на основных ошибках, которые допускают студенты при тригонометрических преобразованиях.
I. Допускают ошибку вида:
а) 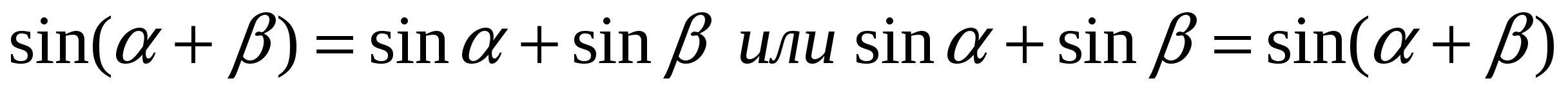
б) 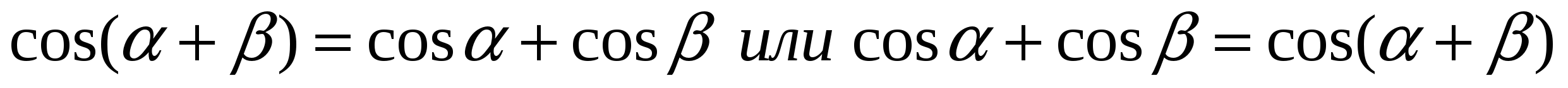
в) 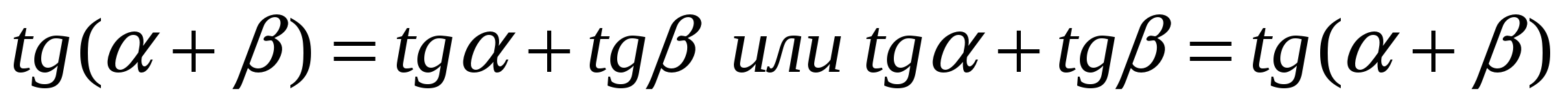
Чтобы предупредить ошибки такого рода при преобразованиях тригонометрических выражений надо перед разбором теорем сложения рассматривать несколько примеров вида:
а) Взять 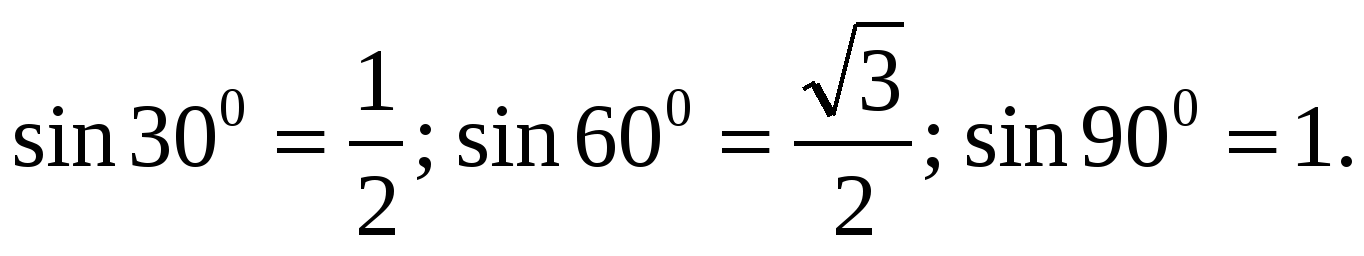
Убедиться в том, что (*) sin(300 + 600) ≠ sin300 + sin600
Так как sin(300 + 600) = sin900 = 1, а sin300 + sin600 = 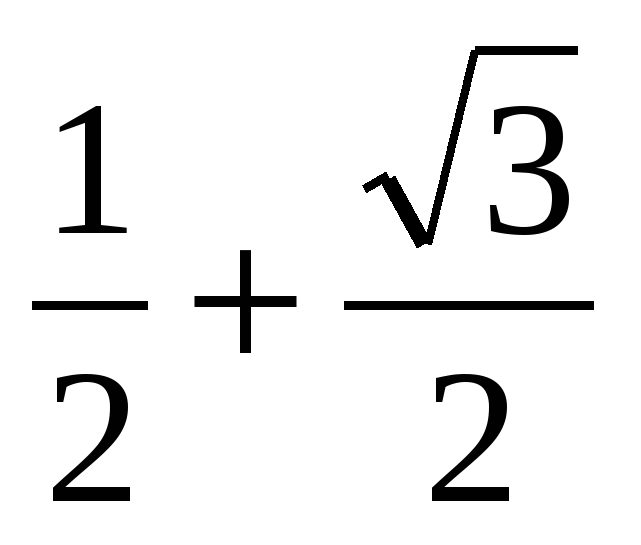 .
.
В левой части равенства (*) получаем 1, а в правой 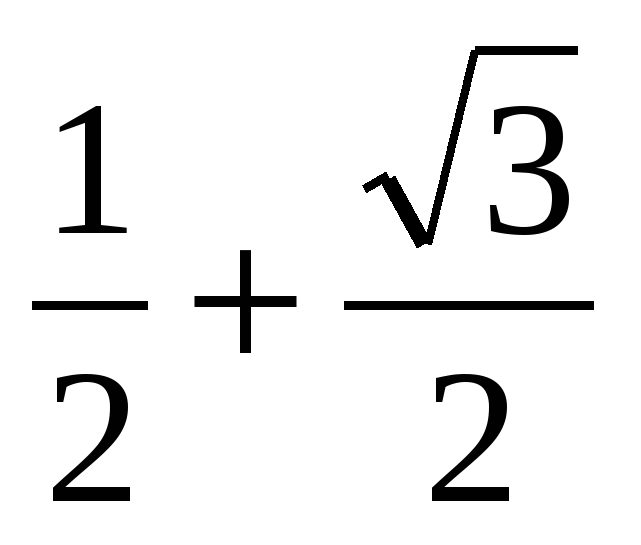 ; 1 ≠
; 1 ≠ 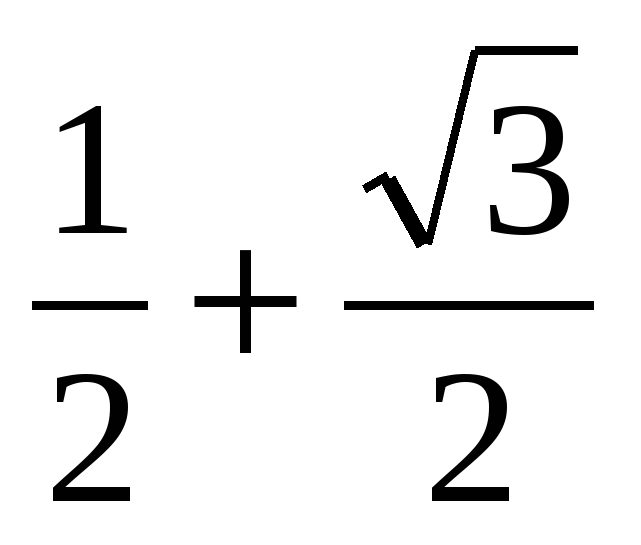 .
.
Следовательно, sin(300 + 600) ≠ sin300 + sin600.
б) Взять 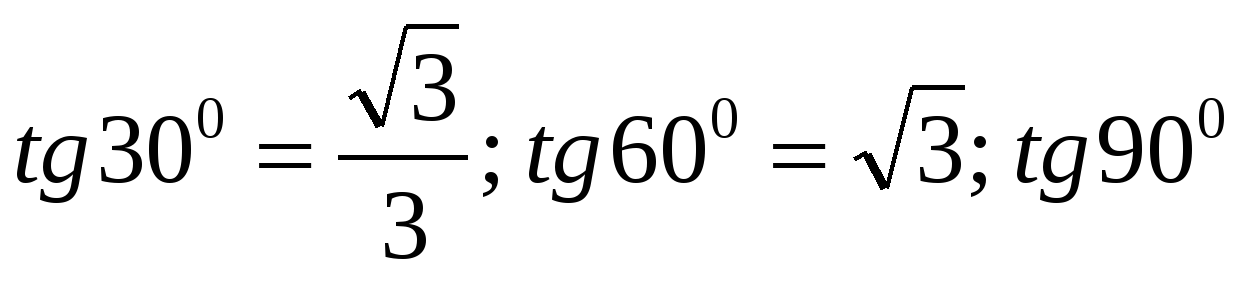 - не существует.
- не существует.
Найти 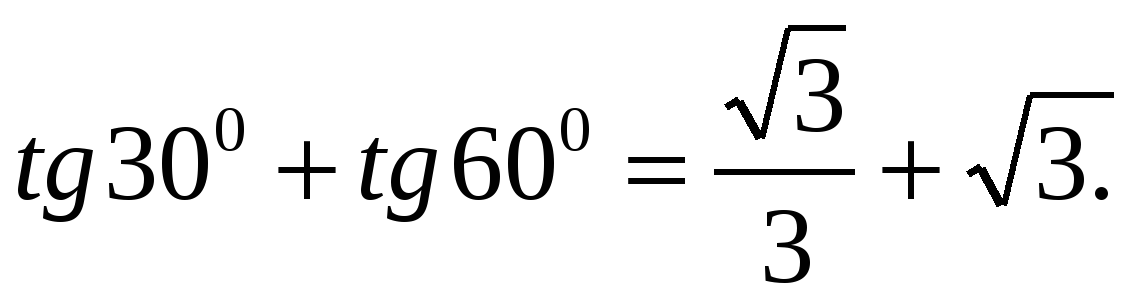
Итак, 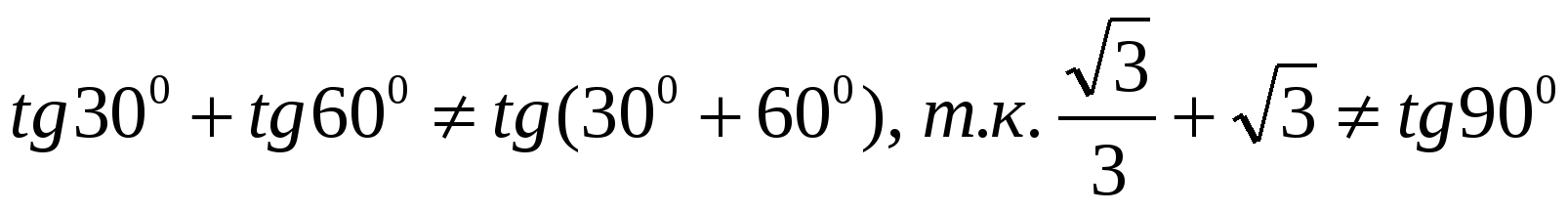
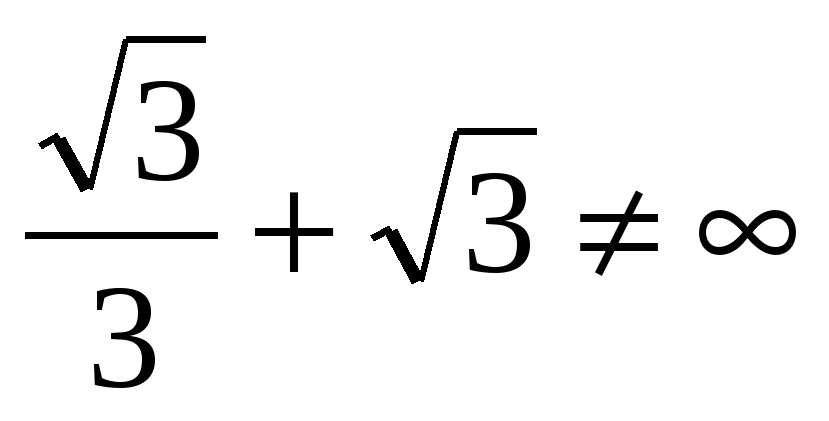
в) 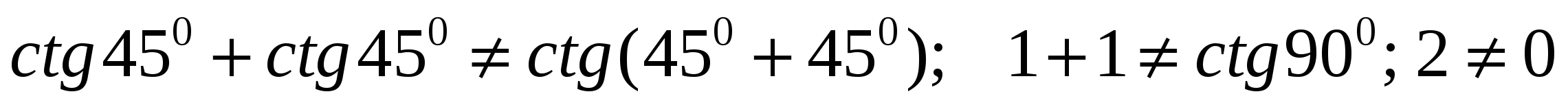
II. В преобразованиях очень часто допускают ошибку, что
tg600=2tg300; sin600=2sin300, т.е. tg2α=2tgα; sin2α=2sinα и т.д.
Предупреждение этой ошибки можно проводить двумя способами:
а) с помощью графика функций.
Из графика видно, что тригонометрические функции не пропорциональны углам, поэтому sin2α ≠ 2sinα; tg2α ≠ 2tgα; cos2α ≠ 2cosα; ctg2α ≠ 2ctgα.
б) sin600≠2sin300; т.е. sin2α≠2sinα, т.к. 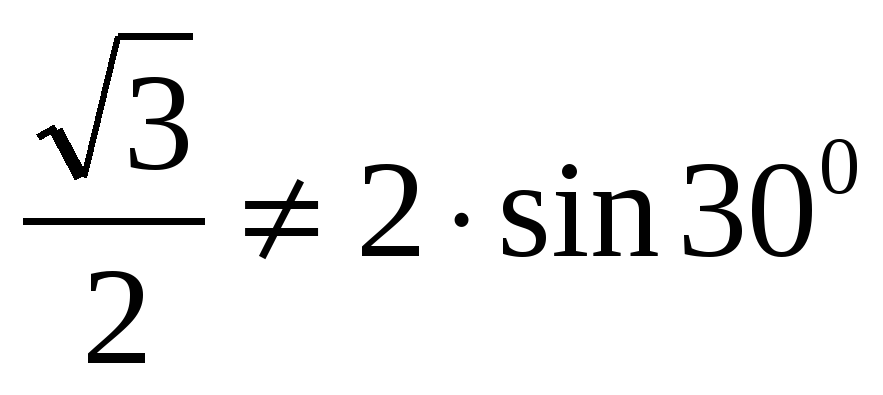 ;
; 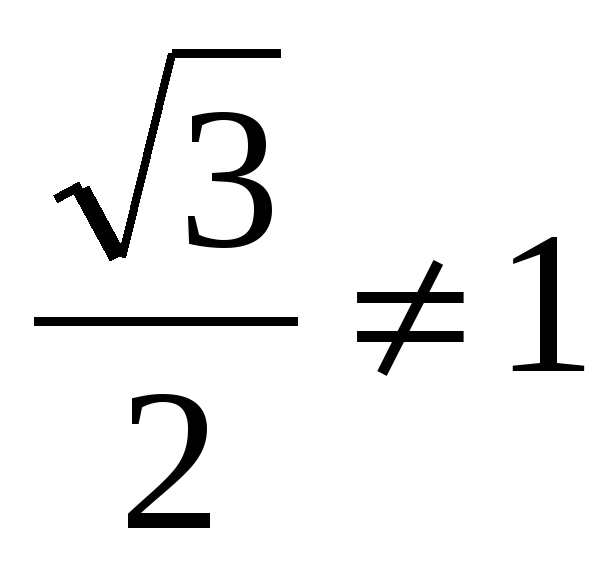 .
.
III. Встречаются ошибки такого вида: tg(α+450) * tg(α+450) = tg2(α+450)2, когда, умножая функцию угла на функцию того же угла, студенты возводят угол в квадрат.
Надо записывать: tg(α+450) * tg(α+450) = tg2(α+450); 
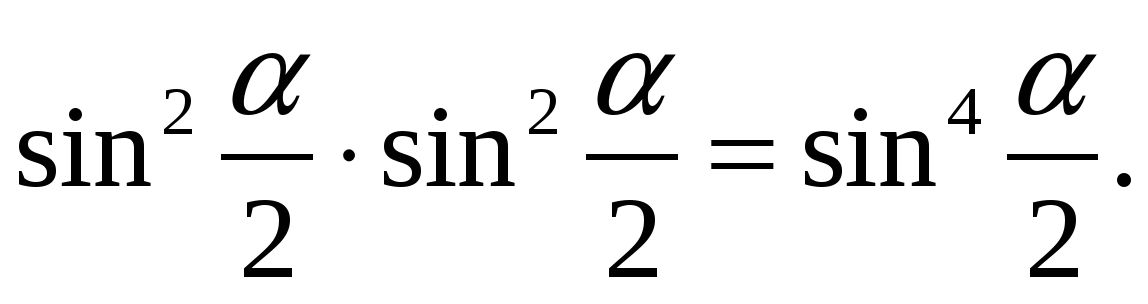
Предупредить ошибку возведения угла в квадрат (в степень) или умножение угла на угол можно двумя способами:
1) Проверить допускаемую ошибку на примере:
tg300* tg300 ≠ tg2(9000), т.к. 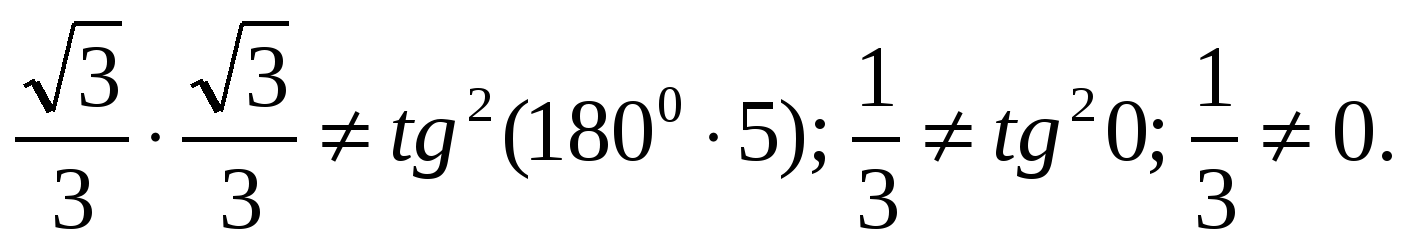
2) Сравнением с помощью:
Перед студентами поставить вопрос: «В чем измеряется площадь?». Площадь измеряется в единицах длины: км, м, дм и т.д. выражение м2=(длина)2=S – площадь.
Выражение (градус)2 не имеет смысла, т.к. нет величины, имеющей измерение (градус)2. Следовательно, угол в квадрат (в степень) возводить нельзя.
IV. Встречается ошибка вида: 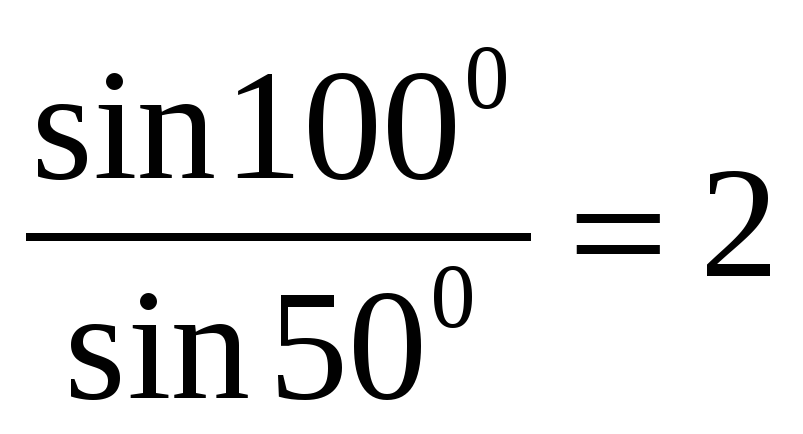
Устранить ошибку такого рода можно двумя способами:
1)
2) тригонометрические функции не пропорциональны углам
V. Студенты не умеют применять знания алгебры при изучении тригонометрии, при тригонометрических преобразованиях.
Например:
1) Упростить выражение: . Не все студенты сразу применяют квадрат суммы двух выражений. В таких случаях надо ставить перед студентами вопрос: «Чему равняется (a + b)2?» Ответ студенты дают верный. Затем надо ставить вопрос: «Что такое sinα?» После получения точного ответа еще раз обратить внимание, что sinα – это число. Теперь перед студентами поставить вопрос: «Что же такое ?» Студенты теперь дают верный ответ.
2) Допускают ошибку вида:
Чтобы устранить эту ошибку надо поставить перед студентами вопросы: «Какое действие надо произвести? Сколько сомножителей в произведении? Назвать все сомножители? Здесь первый сомножитель равен 2, второй - ; третий - . Возводя каждый сомножитель в квадрат получаем:
3) Не умеют сокращать дроби. Допускают такого вида ошибку:
Надо приучать студентов в тригонометрических преобразованиях функции разных аргументов приводить к функциям одного угла:
VI. При решении уравнений сокращаются обе части на множитель, содержащий неизвестный угол.
Например: Решить уравнение: . При решении уравнений такого вида сокращают на . Чтобы предупредить такую ошибку, надо вспомнить, какие действия над уравнениями нарушают их равносильность. Если сократим обе части на , то потеряем корни, значит сокращать нельзя, надо перенести в левую часть и разложить левую часть на множители.
VII. При решении уравнения cos(x – 100) = 0 некоторые студенты пишут х - 100 = 0 и х = 100, а это не верно. Для устранения этой ошибки ставится вопрос: «Косинус какого угла равен 0?» Ответ дают студенты верный, что cosx = 0 и х = 900 + 1800k.
Тогда переходить к решению данного уравнения cos(x – 100) = 0. Получаем х - 100 = 900 + 1800k, х = 1000 + 1800k.
VIII. При решении уравнений вида sin2x = 1,5 студенты допускают две ошибки:
1) чтобы устранить эту ошибку, надо еще раз вспомнить определение тригонометрической функции синус угла и обратить внимание на то, что синус угла – это единое целое, что это число и разрывать его нельзя.
2) При решении уравнения sin2x = 1,5 студенты начинают по таблицам искать угол 2x, по значению функции, забывая, что синус угла по абсолютной величине не превышает 1. Надо здесь поставить вопрос: «Какие значения принимает синус угла? Студенты дают верный ответ: Значит, sinα ≠ 1,5. Синус любого угла по абсолютной величине не больше 1, следовательно sin2х ≠ 1,5, т.е. данное уравнение не имеет решения.
IX. В преобразованиях выражений допускают ошибку в записи.
Например: . Чтобы предупредить ошибку в записи, ставится вопрос: «Чему равен тангенс угла через синус этого угла и косинус того же угла? Студенты дают правильный ответ: Следовательно, надо записывать верно, что.
Заключение
Исследования показали, что тригонометрические функции являются наиболее удобным и наглядным средством для обучения студентов исследованию функций. Преподавание темы «Тригонометрические функции» требует тщательного подбора содержания, средств и методов обучения, то есть разработки эффективной методики.
Изучение тригонометрических функций будет более эффективным в том случае, когда:
1) перед введением тригонометрических функций проведена достаточно широкая пропедевтическая работа с числовой окружностью, которая рассматривается не только как самостоятельный объект, но и как элемент декартовой системы координат;
2) построение графиков осуществляется после исследования свойств тригонометрических функций, исходя из анализа поведения функции на числовой окружности;
3) каждое свойство функции четко обосновано и все они сведены в систему;
4) твердое знание всех формул, как в прямом, так и в обратном порядке.
Для предупреждения и устранения ошибок, допускаемых студентами на занятиях тригонометрии, надо больше уделять внимание решению задач и упражнений, как в аудитории, так и дома. Для развития и поддержания интереса к данной теме следует использовать на занятиях упражнения практического характера по тригонометрии, рассмотреть тригонометрические функции в алгебраических и физических задачах.
Материалы данной исследовательской работы имеют практическую значимость и могут быть использованы преподавателями математики ССУЗов при изложении темы «Тригонометрические функции» в курсе математики.
Библиографический список
Алимов Ш.А. Алгебра и начала анализа 10-11. Учебник/Ш.А. Алимов. – М.: Просвещение, 2001. – 286с.
Дадаян А.А. Математика: Учебник/А.А. Дадаян. – 2-е изд. – М.: ФОРУМ: ИНФРА-М, 2007. – 544с.
Дадаян А.А. Сборник задач по математике/А.А. Дадаян. – М.:ФОРУМ: ИНФРА-М, 2007. – 352с.
Колмогоров А.Н. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк./А.Н. Колмагоров, А.М. Абрамов, Ю.П. Дудницын. – М.: Просвещение, 1999. – 320с.
Крамор В.С. Тригонометрические функции: учеб. пособие/В.С. Крамор, П.А. Михалов. – М.: Просвещение, 1979. – 120с.
Мишин В.И. Методика преподавания математики в средней школе (Частная методика)/В.М. Мишин. – М.: Просвещение, 1987. – 420с.
Мордкович А.Г. Методические проблемы изучения тригонометрии в общеобразовательной школе/А.Г. Мордкович//Математика в школе. – 2002.- №6. – С. 32-38.
Мордкович А.Г. Алгебра и начала анализа 10-11: Учеб. для общеобр. учреждений/А.Г. Мордкович. – М.: Мнемозина, 2003. – 376с.
Цукарь А.Я. Упражнения практического характера по тригонометрии/А.Я. Цукарь// Математика в школе. – 1993. -№2. – С. 75-77.
15







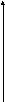 Y
Y 

 P
P
 О
О 

















