Четность, нечетность, периодичность тригонометрических функций

ЧЕТНОСТЬ, НЕЧЕТНОСТЬ, ПЕРИОДИЧНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ

НОВЫЙ МАТЕРИАЛ

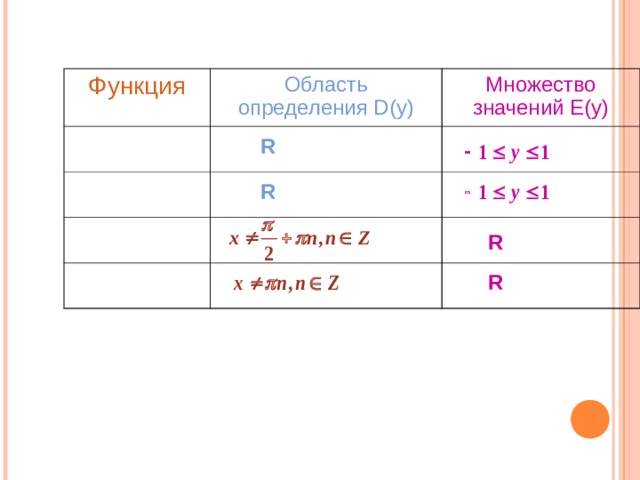
Функция

Область определения D(y)

y=sin x

Множество значений E(y)

y=cos x

y=tg x

y=ctg x

R

R

R

R

ДОМАШНЕЕ ЗАДАНИЕ

№ 1 (4,6), № 2 (4,6),

№ 3 (1,2), № 5 (2)

стр.6

РЕШЕНИЕ УПРАЖНЕНИЙ

1. Найдите область определения функции:

РЕШЕНИЕ УПРАЖНЕНИЙ

2. Найти множество значений функции:

РЕШЕНИЕ УПРАЖНЕНИЙ

3. Найдите область определения функции:

Решение

0









0

•

-1

РЕШЕНИЕ УПРАЖНЕНИЙ

3. Найдите область определения функции:

ЧЕТНОСТЬ И НЕЧЕТНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ

11 класс

ДОМАШНЕЕ ЗАДАНИЕ

П.1.3

№ 18, 32(а.б.в)

Функции

Чётные

Ни чётные,

ни нечётные

Нечётные

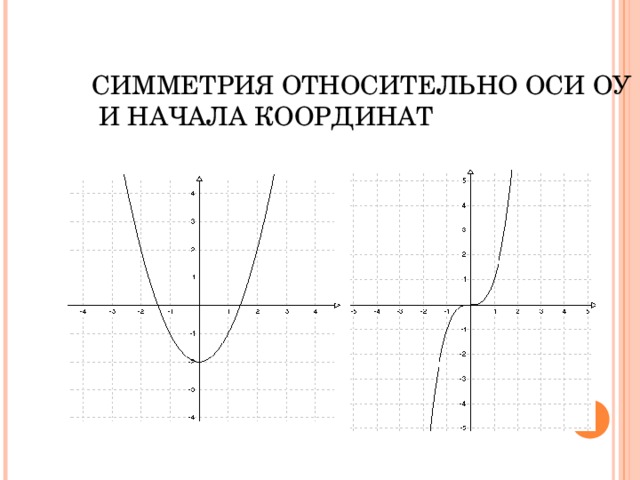
СИММЕТРИЯ ОТНОСИТЕЛЬНО ОСИ ОУ И НАЧАЛА КООРДИНАТ

ЧЕТНЫЕ ФУНКЦИИ

• Функция y = f(x) называется четной, если для любого х из области определения функции верно равенство f(-x) = f(x).
• Чтобы узнать является ли функция четной нужно в функцию f(x) вместо переменной х поставить переменную( –x ).

ЧЕТНЫЕ ФУНКЦИИ

• Например: является ли четной функция f(x) = 3x 2 + 2
• f (-x) = 3(-x) 2 + 2 = 3x 2 + 2 = f(x) – функция четная

ЧЕТНЫЕ ФУНКЦИИ

• Проверим являются ли данные функции четными

• f( - x) = 2(-x) 4 – 3(-x) 2 = 2x 4 - 3x 2 - четная
• f ( - x) = (- x ) 3 – 2 (- x ) 2 = – x 3 – 2x 2 Не является четной

• f(x) = 2x 4 - 3x 2
• f (x) = x 3 - 2x 2

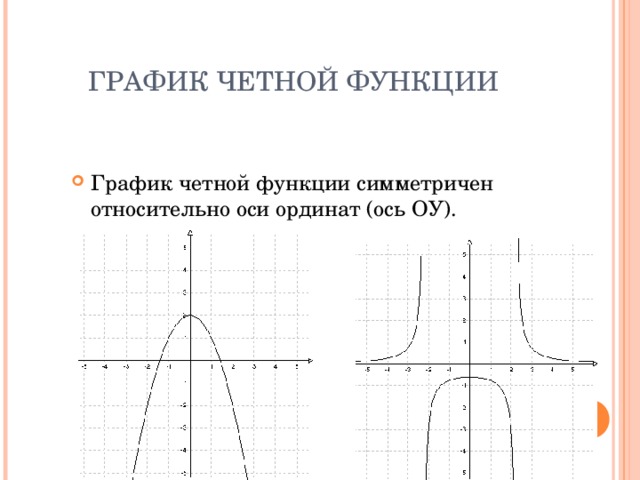
ГРАФИК ЧЕТНОЙ ФУНКЦИИ

• График четной функции симметричен относительно оси ординат (ось ОУ).

НЕЧЕТНЫЕ ФУНКЦИИ

• Функция y = f(x) называется нечетной, если для любого х из области определения функции верно равенство

f(-x) = - f(x).

• чтобы узнать является ли функция нечетной нужно в функцию f(x) вместо переменной х поставить переменную ( – x ) и получить первоначальную функцию с противоположными знаками .

НЕЧЕТНЫЕ ФУНКЦИИ

• Например: является ли нечетной функция f(x) = 3x 3 + х
• f (-x) = 3(-x) 3 + (-х) = - 3x 3 - х = -( 3x 3 + х)=

= - f(x) – функция нечетная

НЕЧЕТНЫЕ ФУНКЦИИ

• Проверим являются ли данные функции нечетными

• f ( - x) = 2(-x) 4 + 3(-x) = = 2x 4 - 3x - не является нечетной
• f ( - x) = (- x ) 3 – 2 (- x ) = – x 3 + 2x нечетная

• f(x) = 2x 4 + 3x
• f (x) = x 3 - 2x

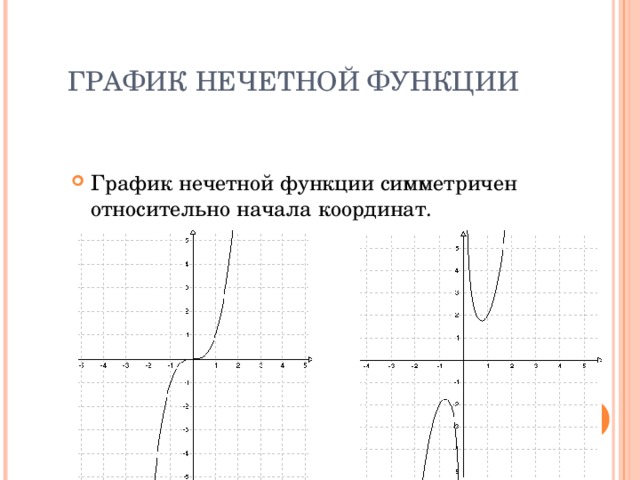
ГРАФИК НЕЧЕТНОЙ ФУНКЦИИ

• График нечетной функции симметричен относительно начала координат.

ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ

• Функции могут быть как четными, нечетными , так и ни четными, ни нечетными.

Пример: y (x) = x 2 + 2x

y(-x) = (-x) 2 + 2(-x) = x 2 - 2x

Для любого значения x верны равенства :

• Sin(-x) = -Sin x Cos(-x) = Cos x
• Sin(-x) = -Sin x Cos(-x) = Cos x
• Sin(-x) = -Sin x
• Cos(-x) = Cos x

Следовательно :

y= Sin x – нечетная функция

y= Cos x – четная функция

Так как для любого значения x из области определения функции

y = tg x верно равенство

tg(-x) = -tg x ,

то y = tg x – нечетная функция.

ПРИМЕР

Выяснить, является ли функция

y = 2 + Sin 2 x четной или нечетной.

Решение :

y(-x) = 2 + Sin 2 (-x) = 2 + (-Sin x) 2 =

=2 + Sin 2 x = y(x) 

 y = 2 + Sin 2 x – четная функция .

Пример: определите, является ли данная функция четной или нечетной

Решение:

Работа в тетрадях

Определите, являются ли данные функции четными или нечетными:

Разбейте функции на три группы:

• четные
• нечетные
• не являются ни четными, ни нечетными

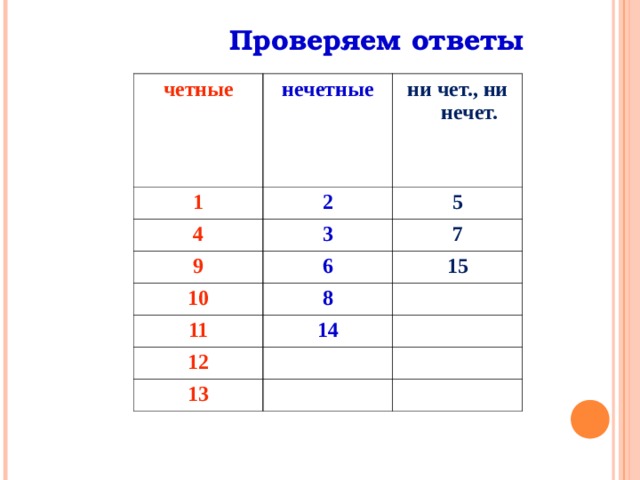
Проверяем ответы

четные

нечетные

1

ни чет., ни нечет.

2

4

5

3

9

10

7

6

15

8

11

14

12

13

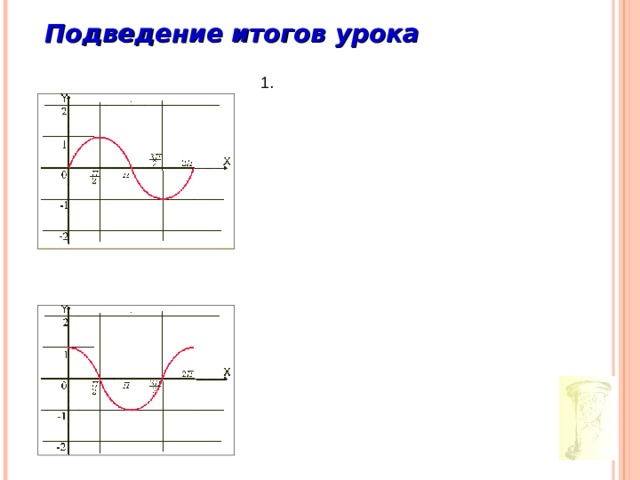
Подведение итогов урока

• y=sinx – нечетная функция,

т.к. sin(-x)=-sinx

График функции симметричен относительно начала координат

2. y=cosx – нечетная функция,

т.к. cos(-x)=cosx

График функции симметричен относительно оси Оу

ЧЕТНОСТЬ, НЕЧЕТНОСТЬ, ПЕРИОДИЧНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ

11 класс

Для любого значения x верны равенства :

• Sin (x + 2 π ) = Sin x Cos (x + 2 π ) = Cos х
• Sin (x + 2 π ) = Sin x Cos (x + 2 π ) = Cos х
• Sin (x + 2 π ) = Sin x
• Cos (x + 2 π ) = Cos х

Следовательно, значения Sin и Cos периодически повторяются при изменении аргумента на 2 π .

Такие функции называются периодическими с периодом 2 π .

Функция f(x) называется периодической , если существует такое число T ≠ 0 , что для любого x из области определения этой функции выполняется равенство

f(x – T) = f(x) = f(x + T).

Число T называется периодом функции f(x).

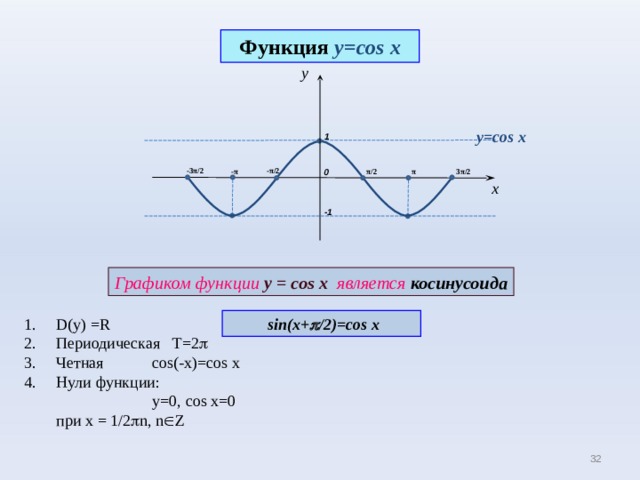
Функция y = cos x

y

y=cos x

1

-3 π /2

- π /2

π /2

π

3 π /2

0

- π

x

-1

Графиком функции у = cos x является косинусоида

• D(y) =R
• Периодическая Т=2 
• Четная cos(-x)=cos x
• Нули функции:

у=0, cos x=0 при х = 1/2  n, n  Z

sin(x+  /2)=cos x

32

32

ПОКАЖЕМ, ЧТО ЧИСЛО 2 Π ЯВЛЯЕТСЯ НАИМЕНЬШИМ ПОЛОЖИТЕЛЬНЫМ ПЕРИОДОМ ФУНКЦИИ Y = COS X.

Пусть Т › 0 – период косинуса, т.е. для любого x выполняется равенство

Cos (x + T) = Cos x. Положив x = 0 , получим Cos T = 1. Отсюда T = 2 π k, k є Ζ . Так как Т › 0, то Т может принимать значения 2 π , 4 π , 6 π , …, и поэтому период не может быть меньше 2 π .

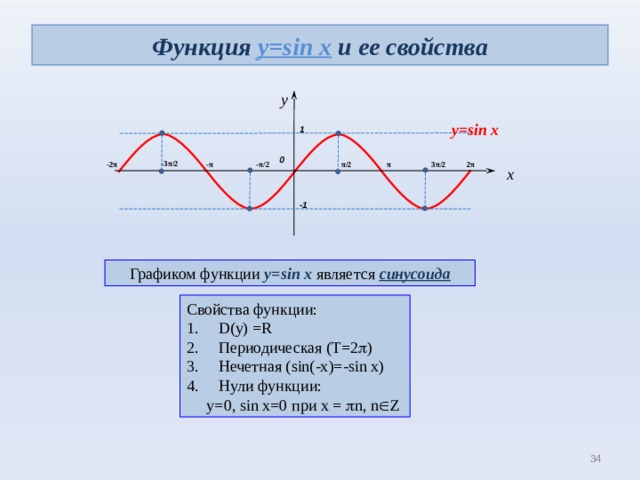
Функция y=sin x и ее свойства

y

y=sin x

1

0

-3 π /2

3 π /2

π /2

- 2 π

2 π

- π /2

- π

π

x

-1

Графиком функции y=sin x является синусоида

Свойства функции:

• D(y) =R
• Периодическая (Т=2  )
• Нечетная ( sin(-x)=-sin x)
• Нули функции:

у=0, sin x=0 при х =  n, n  Z

34

АНАЛОГИЧНО МОЖНО ДОКАЗАТЬ, ЧТО НАИМЕНЬШИЙ ПОЛОЖИТЕЛЬНЫЙ ПЕРИОД ФУНКЦИИ Y = SIN X ТАКЖЕ РАВЕН 2 Π

Пример :

Доказать, что f(x) = Sin 3x – периодическая функция с периодом ( 2 π ) /3.

Доказательство :

Данная функция определена для всех x є R , поэтому достаточно показать, что для любого x верно равенство f(x + T) = f(x) .

f(x + (2 π )/3) = Sin 3(x + (2 π )/3) =

= Sin (3x + 2 π ) = Sin 3x = f(x)

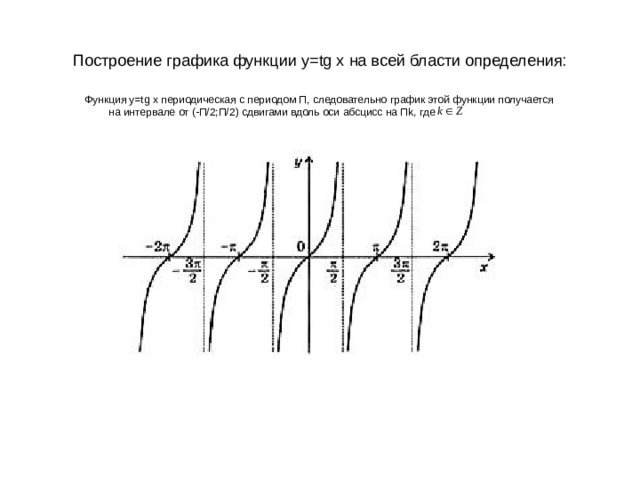
Построение графика функции у= tg x на всей бласти определения:

Функция у= tg x периодическая с периодом П, следовательно график этой функции получается на интервале от (-П/2;П/2) сдвигами вдоль оси абсцисс на П k, где

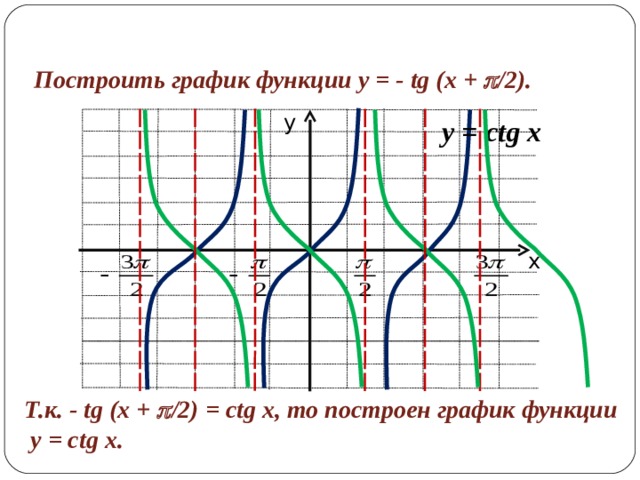
Построить график функции y = - tg (x +  /2) .

у

y = ctg x

х

Т.к. - tg (x +  /2) = ctg x , то построен график функции

y = ctg x .

ПОКАЖЕМ, ЧТО ФУНКЦИЯ Y= TG X ЯВЛЯЕТСЯ ПЕРИОДИЧЕСКОЙ С ПЕРИОДОМ Π .

Если x принадлежит области определения этой функции, т.е. x ≠ - π /2 + π n, n є Ζ , то по формулам приведения получаем

tg(x – π ) = -tg( π – x) = -(-tg x) = tg x

tg(x + π ) = tg x

Таким обтазом, tg(x – π ) = tg x = tg(x + π ). Следовательно, π – период функции у = tg x.

ПОКАЖЕМ, ЧТО Π – НАИМЕНЬШИЙ ПОЛОЖИТЕЛЬНЫЙ ПЕРИОД ФУНКЦИИ Y = TG X.

Пусть Т – период тангенса, тогда tg(x + T) = tg x, откуда при x = 0 получаем tg T = 0, T = k π , k є Ζ . Так как наименьшее целое положительное k равно 1, то π – наименьший положительный период функции y = tg x.

ДОКАЗАТЬ, ЧТО У = TG (X/3) – ПЕРИОДИЧЕСКАЯ ФУНКЦИЯ С ПЕРИОДОМ 3 Π .

Доказательство :

Так как tg ((x + 3 π )/3) = tg (x/3 + π ) = tg (x/3)

и

tg((x - 3 π )/3) = tg(x/3 – π ) = tg (x/3), то tg(x/3) – периодическая функция с периодом 3 π .