Решение неравенств методом рационализации

Решение неравенств методом рационализацииАвтор Сергей Валерьевич

Данная статья посвящена разбору решенией неравенств (логарифмических и неравенств с модулем) методом рационализации. Данный метод становится в последнее время всё более популярным, поскольку помогает существенно упростить решение неравенств, которые встречаются во второй части профильного ЕГЭ по математике. Так что, если вы готовитесь к сдаче этого экзамена и не знакомы с решением неравенств методом рационализации, данная статья может оказаться для вас чрезвычайно полезной.

«Стандартный» метод решения логарифмических неравенств

Рассмотрим традиционный метод решения логарифмического неравенства на конкретном примере.

Вне зависимости от того, каким методом вы решаете то или иное логарифмическое неравенство, начинать всегда нужно с области допустимых значений. Основание логарифма должно быть положительным и не равным 1, а выражение, стоящее под знаком логарифма, — положительным. То есть область допустимых значений в нашем примере определяется следующей системой:

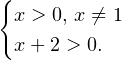
Легко видеть, что решением данной системы является промежуток: .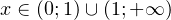

Теперь, используя свойства логарифмов, представим двойку справа в виде логарифма с основанием 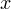. Тогда неравенства примет вид:

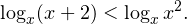
Далее решение неравенства разбивается на два случая:

1) если 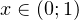. В этом случае в основаниях логарифмов стоят одинаковые числа из интервала 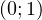. Значит, соответствующие логарифмические функции являются убывающими. Поэтому, опуская знаки логарифмов, нам нужно изменить знак неравенства на обратный. В результате в этом случае приходим к следующему неравенству:

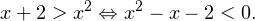
Изобразим соответствующую параболу, ветви которой направлены вверх, пересекающую ось OX в двух точках: 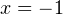и 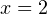, являющихся корнями квадратного трёхчлена :

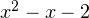Тогда с учётом рассматриваемого ограничения на 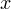получаем для этого случая .

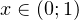2) рассмотрим теперь случай, когда 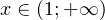. В этом случае оба логарифма будут возрастающими, поэтому после ухода от знаков логарифма, знак неравенства останется прежним. То есть в этом случае исходное логарифмическое неравенство можно заменить следующим:

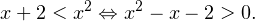
В учётом ограничения на 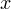решение этого неравенства можно проиллюстрировать на числовой прямой следующим образом:

То есть решение в данном случае имеет вид: .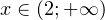

Объединяя решения, полученные в пунктах а) и б), приходим к окончательному ответу, который имеет вид: .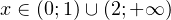

Решение логарифмических неравенств методом рационализации

Описанный в предыдущем параграфе способ является правильным, но при этом чрезвычайно неудобным. Как видите, приходится рассматривать два отдельных случая, что существенно повышает вероятность совершения ошибки. Гораздо проще поступить следующим образом. Перепишем исходное логарифмическое неравенства в виде:

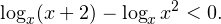
А дальше, в области допустимых значений, то есть при 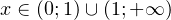(это мы установили выше), данное неравенство можно заменить следующим равносильным ему неравенством:

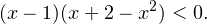
Ну действительно, если 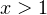, то первая скобка положительна, и на неё можно разделить, не меняя при этом знак неравенства. Если же 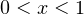, то первая скобка отрицательна, и при делении на неё, знак неравенства изменится на противоположный.

То есть мы получили ровно то же самое, что имели в предыдущем пункте. Но при этом нет необходимости рассматривать два случая. Всё решается в рамках одного единственного неравенства. И хотя этот способ не избавляет нас от необходимости определения области допустимых значений, он всё равно приводит к существенному упрощению решения задачи.

Решаем полученное неравенство методом интервалов. Для этого поменяем знаки во второй скобке, разделим обе части неравенства на -1, поменяв знак неравенства:

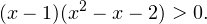
Теперь разложим выражение во вторых скобках на множители:

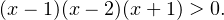
Изобразим на числовой прямой множество решений полученного неравенства (стрелкой обозначена область допустимых значений исходного логарифмического неравенства):

В результате получаем тот же результат, что и в предыдущем параграфе:

.

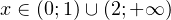Итак, метод рационализации логарифмических неравенств состоит в следующем.

Неравенство вида

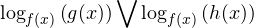
в области его допустимых значений можно заменить равносильным неравенством

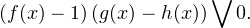
Здесь знак 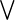означает любой из знаков 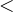, , 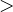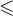или .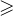

С помощью этого метода можно решать и более сложные логарифмические неравенства. Рассмотрим ещё один пример из реальных прототипов заданий ЕГЭ по математике.

Область допустимых значений данного неравенства определяется следующей системой неравенств:

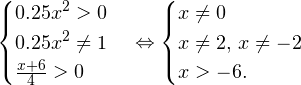
Итак, область допустимых значений задаётся следующим промежутком:

.

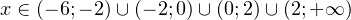Представим единицу справа в виде логарифма с основанием 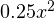и перенесём его в левую сторону неравенства:

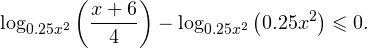
Воспользуемся методом рационализации. В области допустимых значений данное неравенство можно заменить следующим:

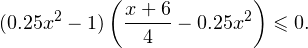
Умножим обе части на -4, поменяв при этом знак неравенства:

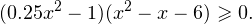
Разложим на множители выражение, стоящее в обеих скобках:

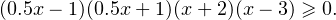
Если умножить обе части на 2 и внести этот множитель во вторую скобку, то получится следующее уравнение:

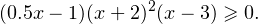
Изобразим на числовой прямой промежутки, на которые разбивают числовую ось корни полученного многочлена слева, определим знаки многочлена в каждом промежутке и выделим решение неравенства с учётом области допустимых значений:

Итак, окончательный ответ:

.
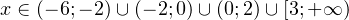