Метод рационализации при решении показательных и логарифмических неравенств
| Из опыта работы учителя математики, физики МОУ «Сольвычегодская СОШ» Ноговицыной Валентины Валериевны |
Решение неравенств методом интервалов достаточно часто приводит к затруднению при вычислении значения функции в промежуточных точках. Чтобы расширить возможности применения метода интервалов, рассмотрим метод рационализации.
Метод рационализации заключается в замене сложного выражения  на более простое выражение
на более простое выражение  , при которой неравенство
, при которой неравенство 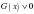 равносильно неравенству
равносильно неравенству 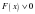 в области определения выражения.
в области определения выражения.
Выделим некоторые выражения F и соответствующие им рационализирующие выражения G, где  - выражения от переменной х
- выражения от переменной х  , а – фиксированное число
, а – фиксированное число  .
.
|

| Некоторые следствия (с учетом ОДЗ неравенства)


|
Рассмотрим примеры сведения логарифмических и показательных неравенств, у которых основание, выражение под знаком логарифма, степень – многочлены. Оказывается, такие неравенства эффективно сводятся к дробно-рациональным или рациональным, причём, полученные решения будут более компактными по сравнению с традиционными.
Сведение логарифмического неравенства к системе рациональных неравенств
Рассмотрим логарифмическое неравенство вида
 , (1)
, (1)
где  - некоторые функции (об их природе будем говорить ниже).
- некоторые функции (об их природе будем говорить ниже).
Стандартный метод решения такого неравенства предполагает разбор двух случаев на области допустимых значений неравенства:
если  , то
, то 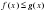 ; 2. если
; 2. если  , то
, то  .
.
Рассмотрев два случая, необходимо объединить ответы. Правда, при рассмотрении второго случая возникает определенный дискомфорт – приходится на 90 процентов повторять выкладки из первого случая (преобразовывать, находить корни вспомогательных уравнений, определять промежутки монотонности знака). Возникает естественный вопрос – можно ли все это как-нибудь рационализировать объединить?
Ответ на этот вопрос содержится в следующей теореме.
Теорема 1. Логарифмическое неравенство 
равносильно следующей системе неравенств:
 (2)
(2)
Доказательство. Начнем с того, что первые четыре неравенства системы (2) задают множество допустимых значений исходного логарифмического неравенства. Обратим теперь внимание на пятое неравенство. Если  , то первый множитель этого неравенства будет отрицателен. При сокращении на него придется изменить знак неравенства на противоположный, тогда получится неравенство
, то первый множитель этого неравенства будет отрицателен. При сокращении на него придется изменить знак неравенства на противоположный, тогда получится неравенство 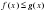 . Если же
. Если же  , то первый множитель пятого неравенства положителен, сокращаем его без изменения знака неравенства, получаем неравенство
, то первый множитель пятого неравенства положителен, сокращаем его без изменения знака неравенства, получаем неравенство  . Таким образом, пятое неравенство системы включает в себя оба случая предыдущего метода. Терема доказана
. Таким образом, пятое неравенство системы включает в себя оба случая предыдущего метода. Терема доказана
Пример 1. Решить неравенство  .
.
Решение. Воспользуемся теоремой 1. Получим следующую систему неравенств:
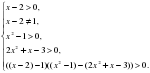
Решая первые четыре неравенства, находим ОДЗ исходного неравенства:

Откуда:  .
.
Решим теперь пятое неравенство системы: .
.
 .
.
 .
.
С учетом найденного ранее ОДЗ, получаем окончательный ответ.
Ответ:  .
.
Сведение показательного неравенства к системе рациональных неравенств
Рассмотрим показательное неравенство вида
 (3)
(3)
где  - некоторые функции.
- некоторые функции.
Традиционное решение такого неравенства приводит к двум случаям:
1. если  , то
, то 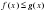 ; 2.если
; 2.если  , то
, то  .
.
Как и в случае с логарифмическим неравенством, имеется возможность значительно укоротить решение задачи, используя метод рационализации. Этот метод основан на следующей теореме.
Теорема 2. Показательное неравенство

равносильно следующей системе неравенств:
(4)
Нетрудно заметить, что система (4) аналогична системе (2) из теоремы 1 (правда, в ней нет требования положительности степеней).
Пример 2. Решить неравенство
 .
.
Решение. Составим систему неравенств, аналогичную системе (4) из теоремы 2:
Решив два первых неравенства, найдем ОДЗ исходного показательного неравенства:

Откуда ОДЗ:  .
.
Далее рассмотрим основное неравенство  , которое приводится к виду:
, которое приводится к виду:  .
.
Корни первого множителя этого неравенства мы нашли ранее:  . Корни второго множителя равны:
. Корни второго множителя равны:  ,
,  ,
,  .
.
Так как  , то
, то  . Применив метод интервалов, получим следующее решение основного неравенства:
. Применив метод интервалов, получим следующее решение основного неравенства:  .
.
Учитывая найденную ранее ОДЗ, получаем окончательный ответ:
 .
.
Пимер 3. Решить систему неравенств
Решение: Рассмотрим решение каждого неравенства отдельно:
(2): введем замену 
- система несовместна, т.к. по первому неравенству 
Выберем решение системы  , т.к.
, т.к.  .
.
Ответ:  .
.
Задания для самостоятельного решения.
1.
2.
3.
4.
5.
6.
Используемая литература:
1. Алгебра и начала анализа: Учеб. для 11 кл. общеобразовательных учреждений /[С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин ] – 5-ое изд. – М.: Просвещение, ОАО «Московские учебники»,2006.
2. А.Г. Корянов, А.А. Прокофьев. Материалы курса «Готовим к ЕГЭ хорошистов и отличников»: лекции 1-4. – М.: Педагогический университет «Первое сентября», 2012.
3. Колесникова, С.И. Математика. Интенсивный курс подготовки к ЕГЭ. Айриспресс 2014г.





 на более простое выражение
на более простое выражение  , при которой неравенство
, при которой неравенство 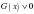 равносильно неравенству
равносильно неравенству 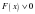 в области определения выражения.
в области определения выражения. - выражения от переменной х
- выражения от переменной х  , а – фиксированное число
, а – фиксированное число  .
.

 , (1)
, (1) - некоторые функции (об их природе будем говорить ниже).
- некоторые функции (об их природе будем говорить ниже). , то
, то 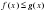 ; 2. если
; 2. если  , то
, то  .
. (2)
(2) .
.