РОССИЙСКАЯ НАУЧНО-СОЦИАЛЬНАЯ ПРОГРАММА
ДЛЯ МОЛОДЕЖИ И СТУДЕНТОВ «ШАГ В БУДУЩЕЕ»
«НЕСТАНДАРТНЫЕ СПОСОБЫ РЕШЕНИЯ
КВАДРАТНЫХ УРАВНЕНИЙ»
ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА НА ИНТЕЛЛЕКТУАЛЬНЫЙ
ФОРУМ МОЛОДЕЖИ «ШАГ В БУДУЩЕЕ»
Автор: Голощапов Виталий Олегович
9 класс МОУ «СОШ №1»
Руководитель: Голощапова Л.А.,
учитель математики МОУ «СОШ №1»
Г. ЧЕЛЯБИНСК
2010
СОДЕРЖАНИЕ
Цели и задачи работы…..………………………………………………….3
Квадратное уравнение и его корни………………………………………..3
Нестандартные способы решения квадратных уравнений………………4
Прием коэффициентов………………………………………………4
Прием переброски…………………………………………………...6
Решение некоторых видов квадратных уравнений………………..7
Использование приемов решения квадратных уравнений………………..8
Выводы……………………………………………………………………….8
Приложения………………………………………………………………….9
Список литературы………………………………………………………….10
ЦЕЛИ И ЗАДАЧИ РАБОТЫ
Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, иррациональных уравнений и неравенств.
В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения.
Однако имеются и другие приёмы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения. Овладение данными приёмами поможет экономить время и эффективно решать уравнения; потребность в быстром решении обусловлена применением системы ЕГЭ.
Целью данной работы является выявление нестандартных способов решения квадратных уравнений. Для этого следует решить ряд задач:
обобщить и систематизировать материал по теме: «Решение квадратных уравнений»;
рассмотреть известные приёмы устного решения квадратных уравнений;
выявить закономерности в решении квадратных уравнений и сформулировать способы решения некоторых типов квадратных уравнений;
составить список заданий для применения нестандартных способов решения квадратных уравнений.
Для достижения поставленных задач нужно использовать такие методы, как изучение литературы и Интернет - источников, анализ, обобщение данных, выдвижение гипотезы и ее доказательство.
КВАДРАТНОЕ УРАВНЕНИЕ И ЕГО КОРНИ
Квадратным уравнением называется уравнение вида ax2+bx+c=0, где х – переменная, а, b, с – некоторые числа, причем а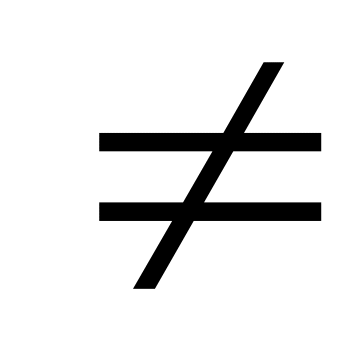 0. Числа а, b, с – коэффициенты квадратного уравнения. Число а называют первым коэффициентом, число b – вторым коэффициентом и число с – свободным членом.
0. Числа а, b, с – коэффициенты квадратного уравнения. Число а называют первым коэффициентом, число b – вторым коэффициентом и число с – свободным членом.
Квадратное уравнение, в котором первый коэффициент равен 1, называют приведенным квадратным уравнением. Если квадратное уравнение разделить на первый коэффициент 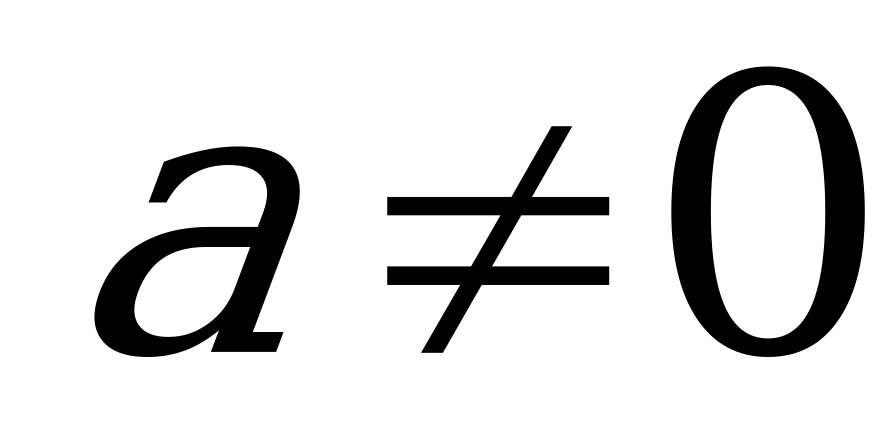 , то получится приведенное квадратное уравнение:
, то получится приведенное квадратное уравнение:
x2+ x+
x+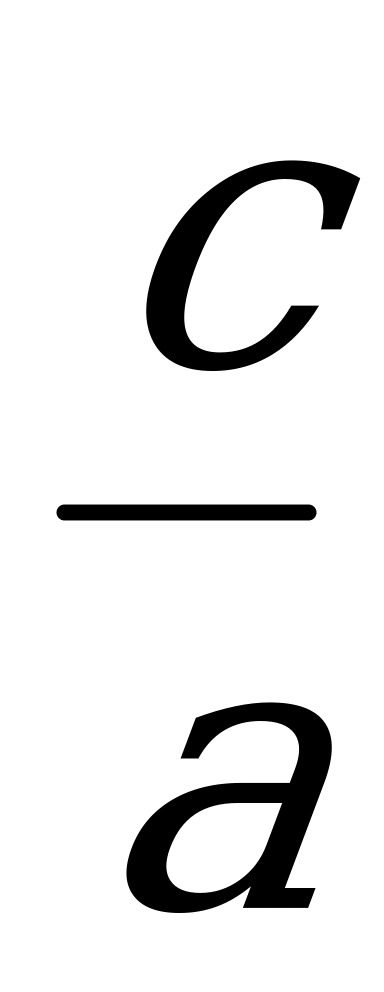 =0. Если
=0. Если  =p,
=p, 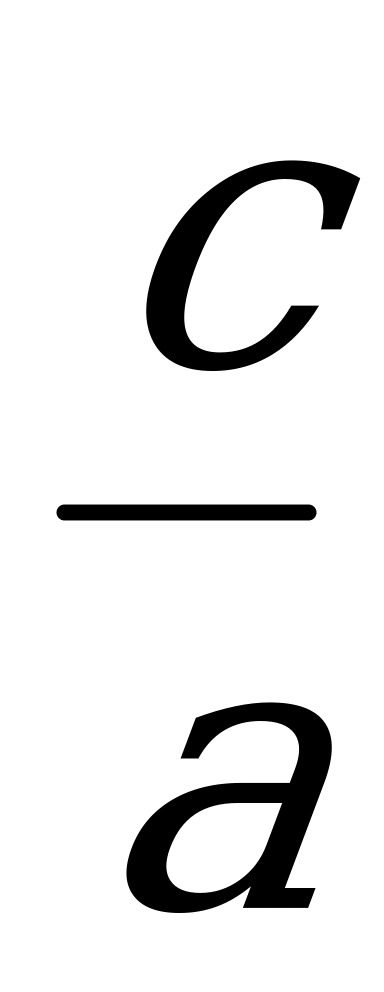 =q, то уравнение примет вид x2+px+q=0.
=q, то уравнение примет вид x2+px+q=0.
Для решения квадратных уравнений существуют формулы:
Для уравнения ax2+bx+c=0 - 
Для уравнения x2+px+q=0 - 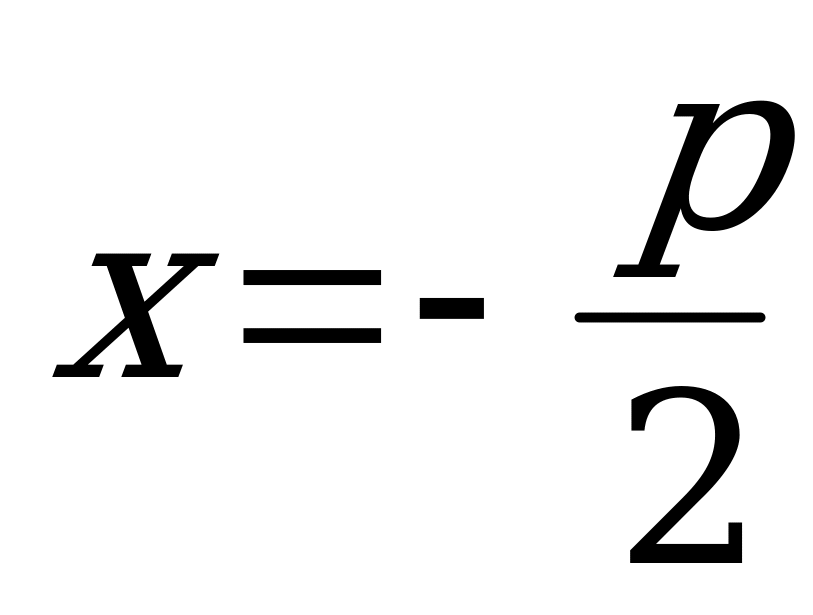
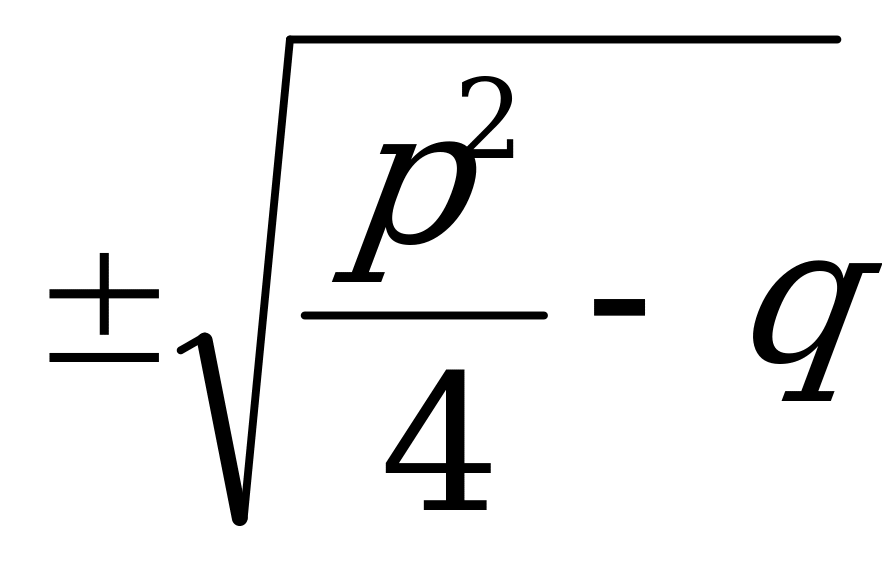
Если b=2k, то 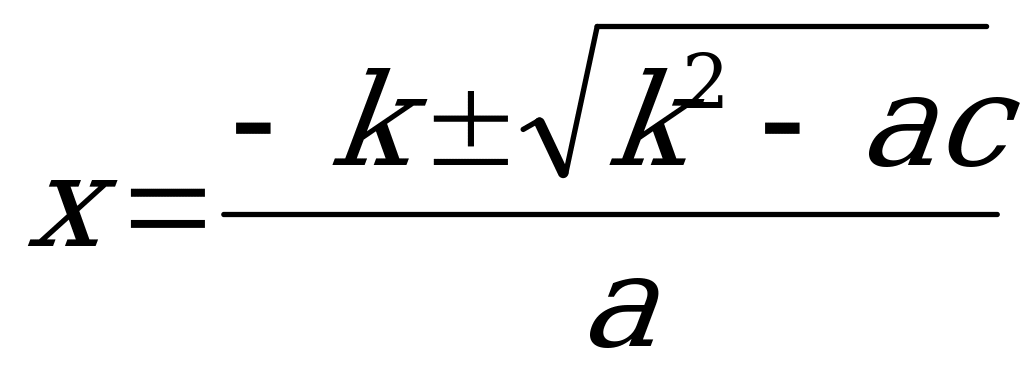
Для решения приведенных квадратных уравнений можно использовать теорему Виета:
Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Дано:
х1 и х2 – корни уравнения x2+px+q=0
Доказать: х1 + х2=-р
х1  х2=q
х2=q
Доказательство:
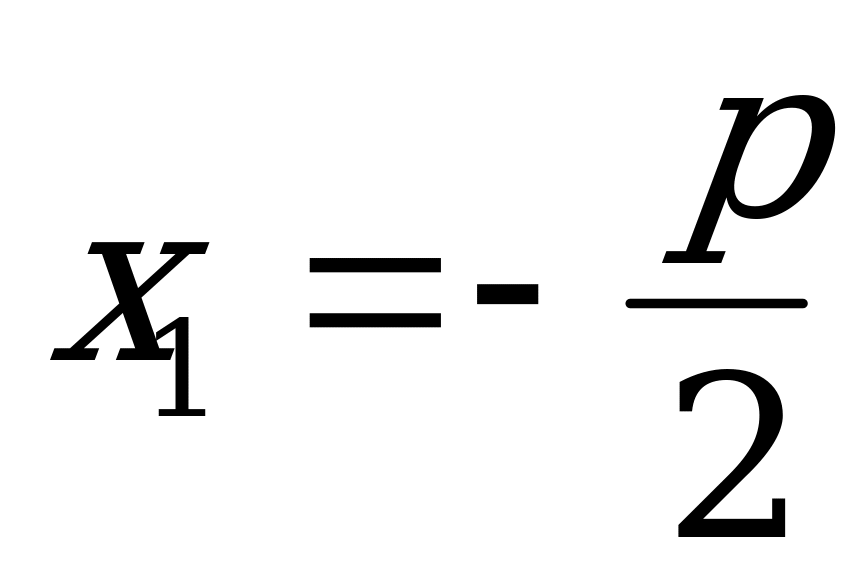
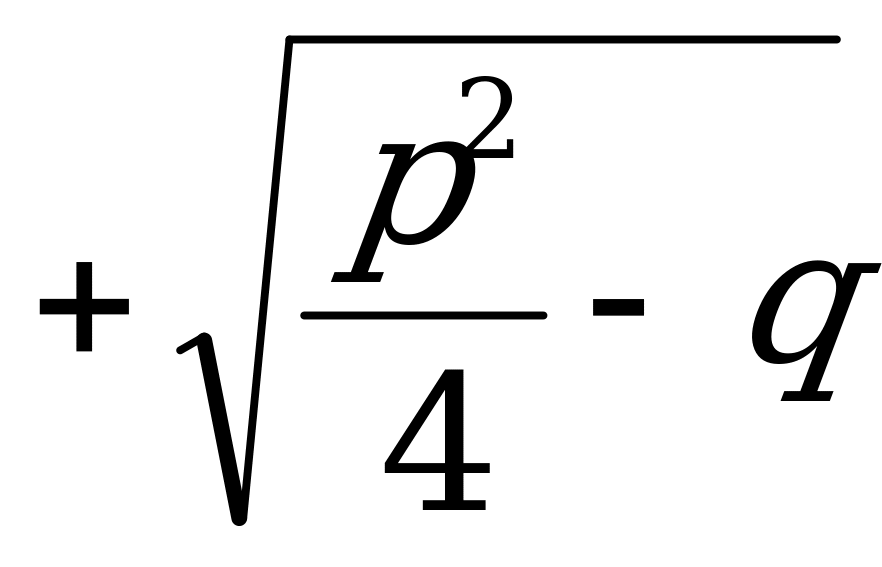 и
и 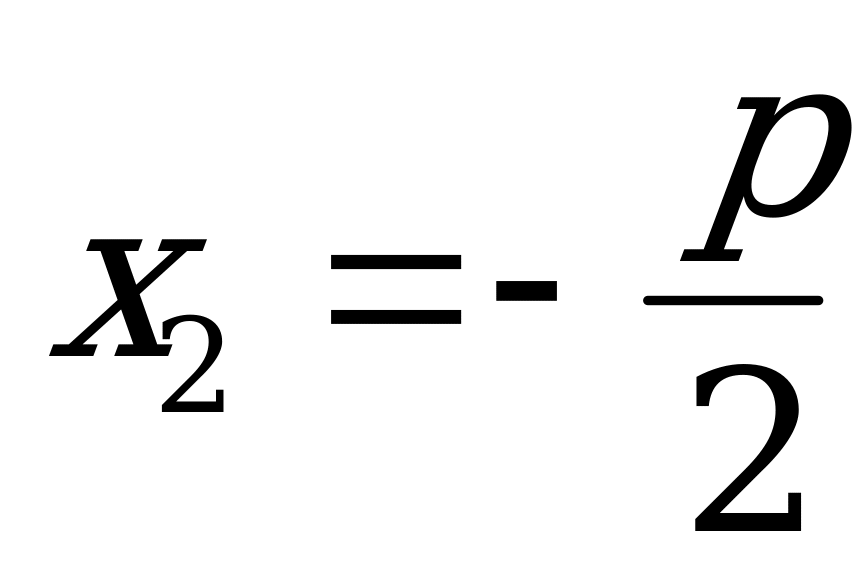

Тогда
х1+х2=
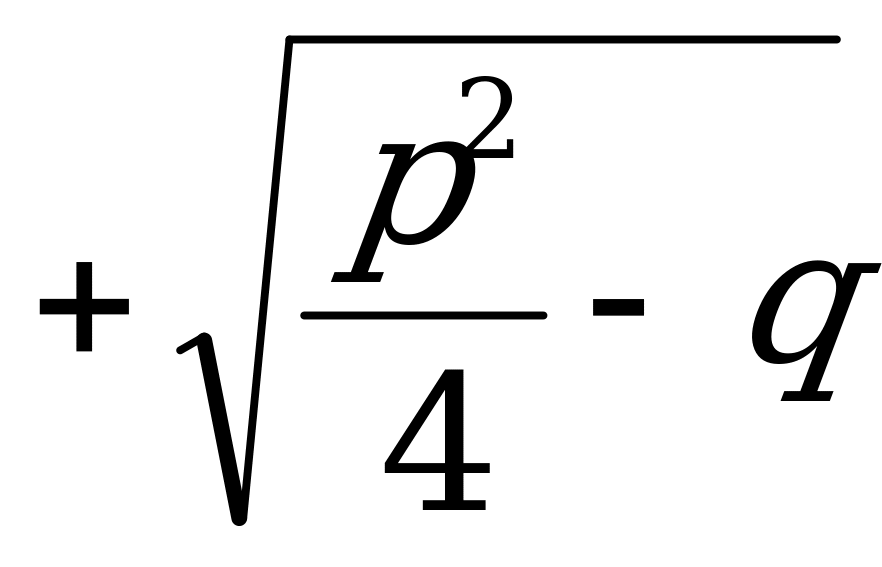

 =
= 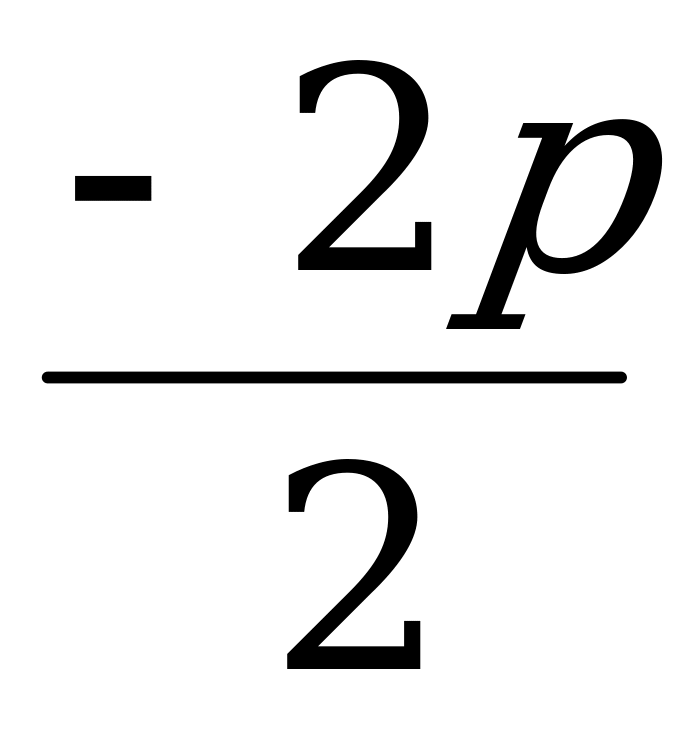 = -р;
= -р;
х1  х2=(
х2=(
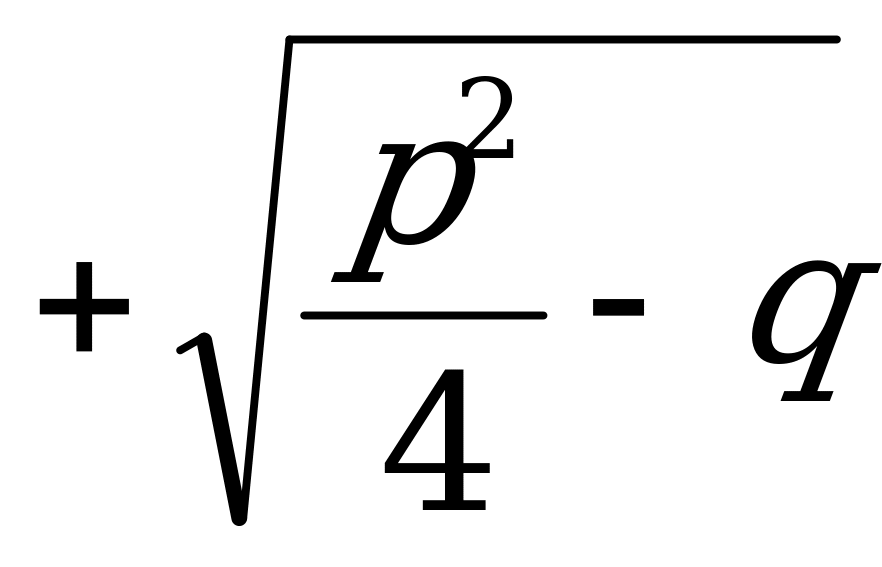 )(
)(
 ) =
) =  = q
= q
Теорема доказана.
Пример. Решить с помощью теоремы Виета уравнение х2 – 9х + 20 = 0.
х1+х2= 9 и х1  х2 = 20
х2 = 20
Нетрудно догадаться, что х1=4, х2=5.
НЕСТАНДАРТНЫЕ СПОСОБЫ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ
I. ПРИЕМ «КОЭФФИЦИЕНТОВ»
Чтобы решить уравнения типа
10х2+2009х+1999=0 или 7х2 – 2010х +2003 = 0, нужно воспользоваться следующими свойствами коэффициентов квадратных уравнений:
Если a + b + c=0 (т.е. сумма коэффициентов равна нулю),
то один из корней квадратного уравнения равен 1, а второй – дроби 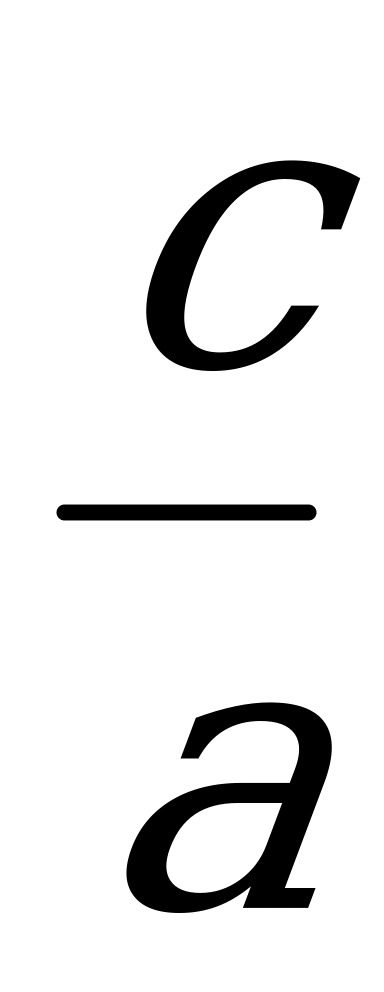 .
.
Дано: ax2+bx+c=0
a + b + c=0
Доказать: х1=1
х2=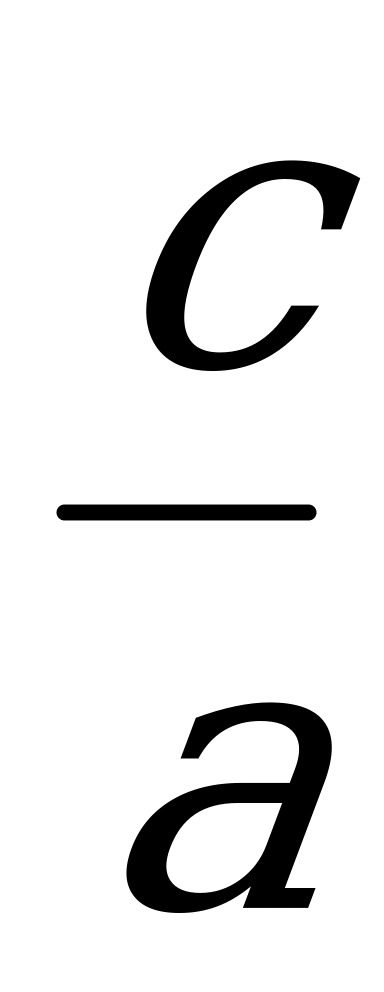
Доказательство: разделим обе части уравнения ax2+bx+c=0 на а 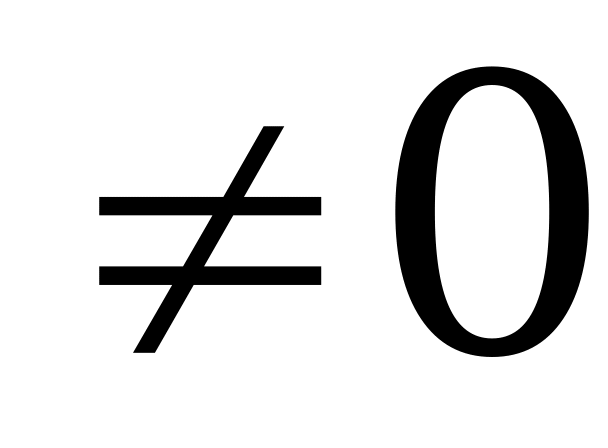 , получим приведённое квадратное уравнение x2+
, получим приведённое квадратное уравнение x2+ x+
x+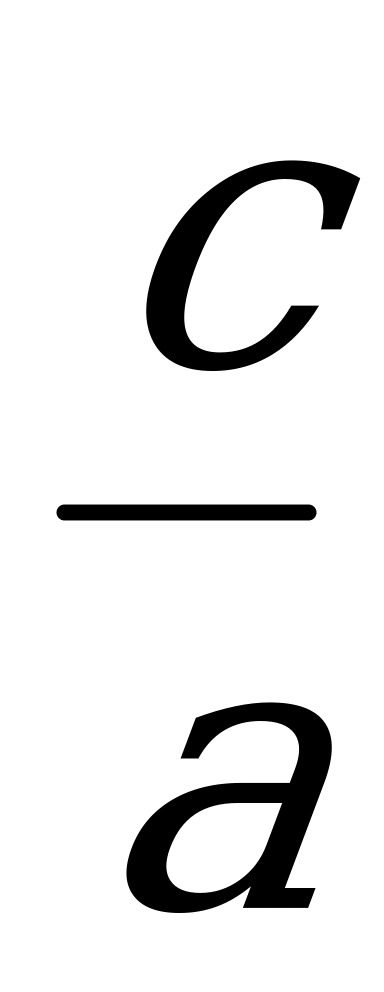 =0.
=0.
По теореме Виета х1 + х2=-
х1  х2=
х2=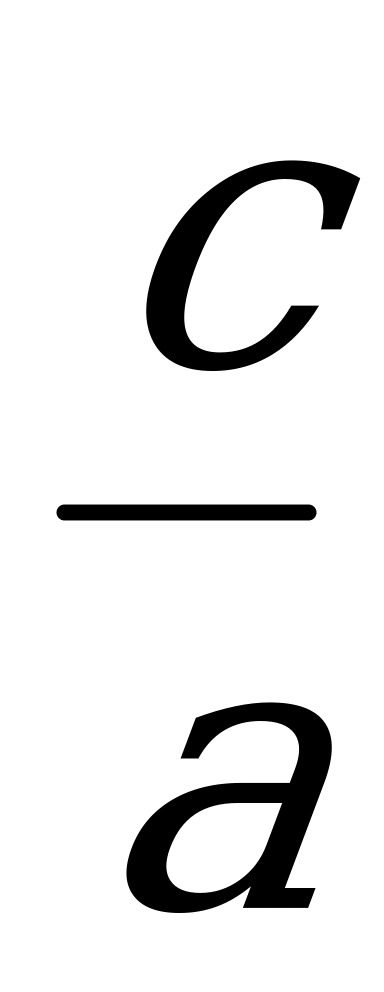
По условию a + b +c =0, откуда b= - a – c.
Значит х1 + х2=-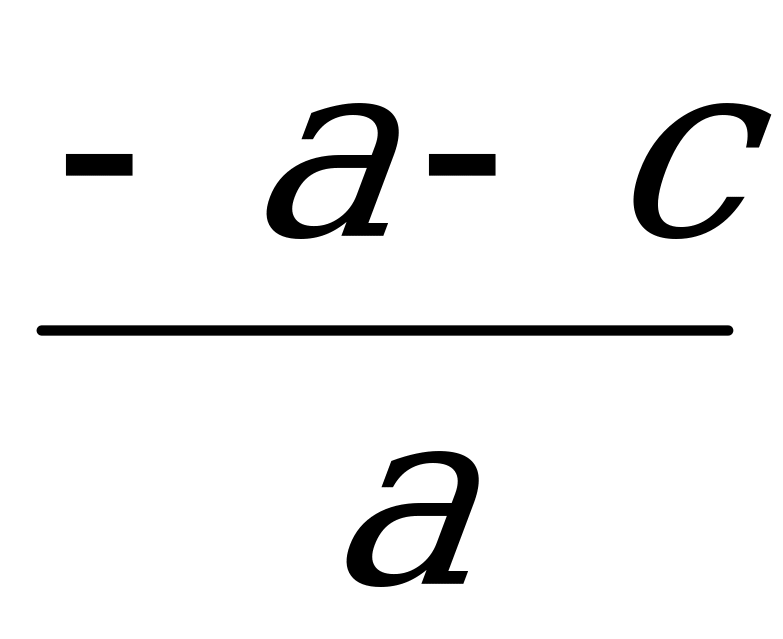 =
=  = 1+
= 1+ 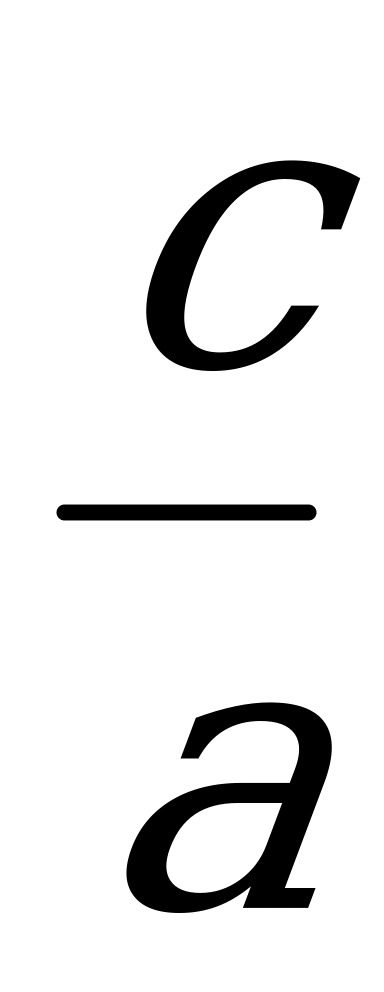 ,
,
х1  х2= 1
х2= 1
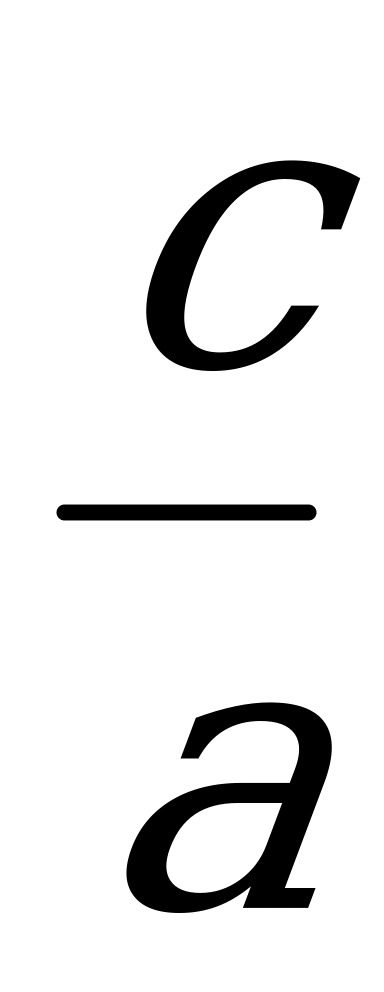
Получаем х1=1, х2=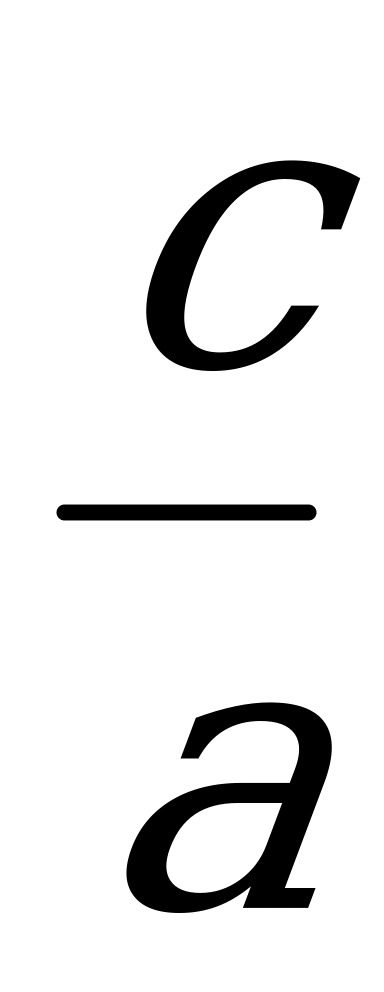 , что и требовалось доказать.
, что и требовалось доказать.
Пример. Решить уравнение а)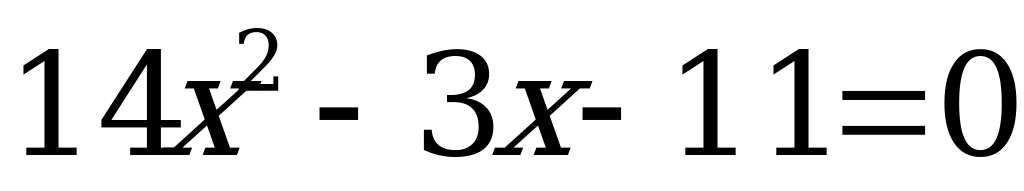
Так как 14 – 3 – 11 = 0, то


б) 7х2 – 2010х +2003 = 0
Так как 7 – 2010 + 2003 = 0, то 
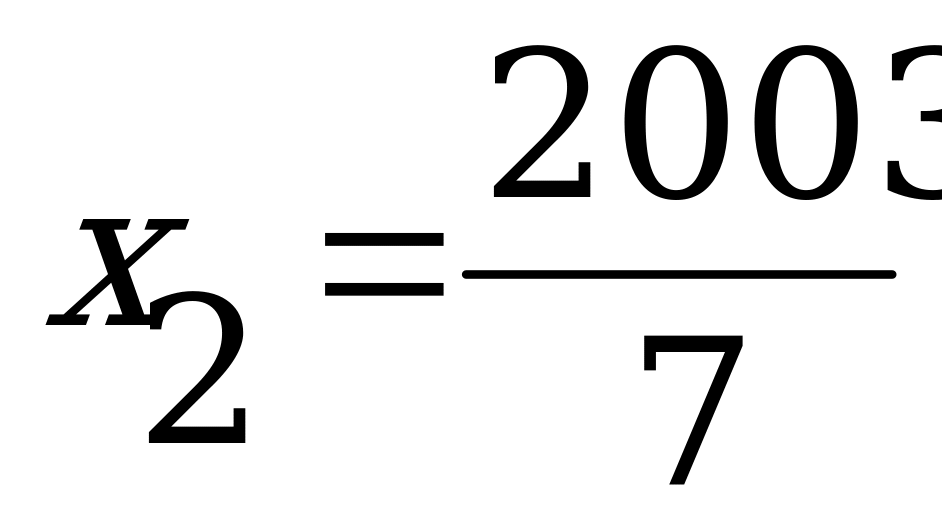
Если a - b + c=0 (или b = а + с, т.е. второй коэффициент равен сумме первого коэффициента и свободного члена),
то один из корней квадратного уравнения равен (-1), а второй –
дроби ( - 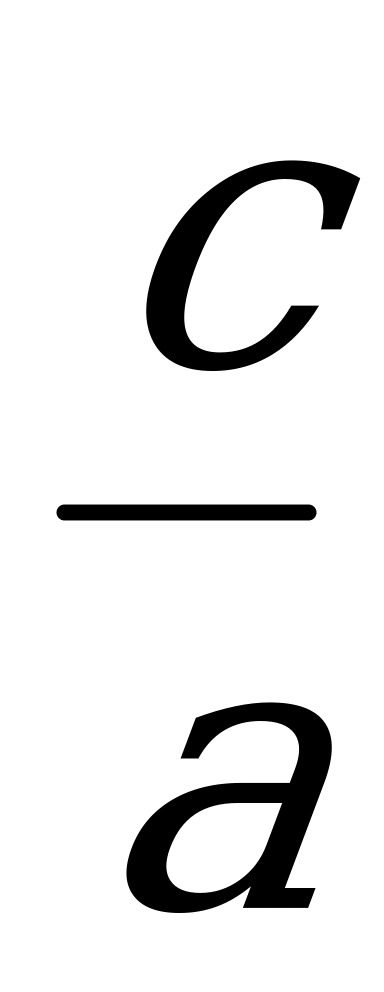 ).
).
Дано: ax2+bx+c=0
a – b + c=0
Доказать: х1= - 1
х2= - 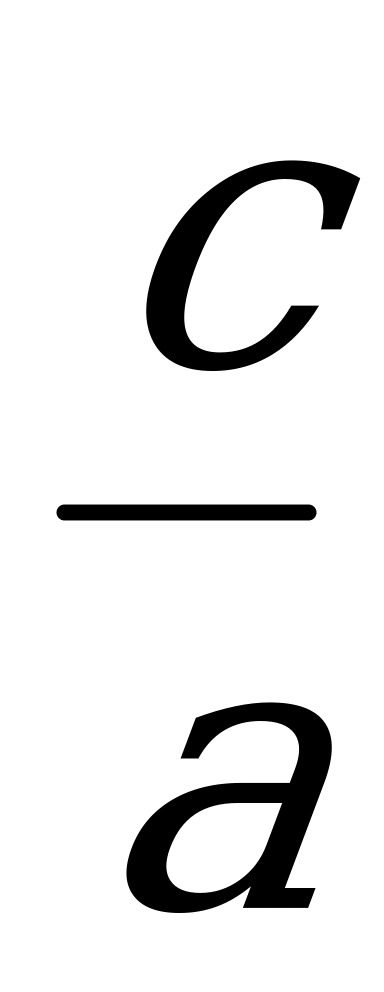
Доказательство: разделим обе части уравнения ax2+bx+c=0 на а 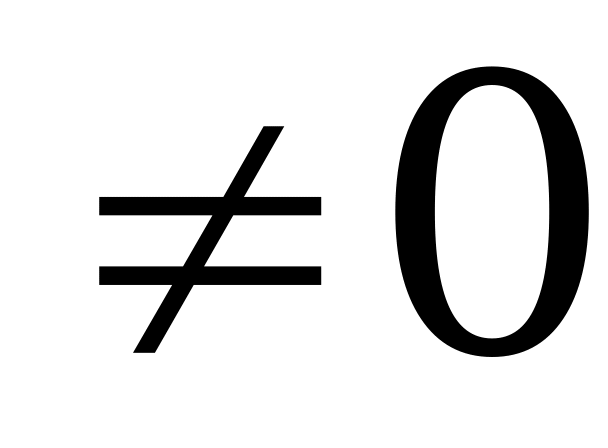 , получим приведённое квадратное уравнение x2+
, получим приведённое квадратное уравнение x2+ x+
x+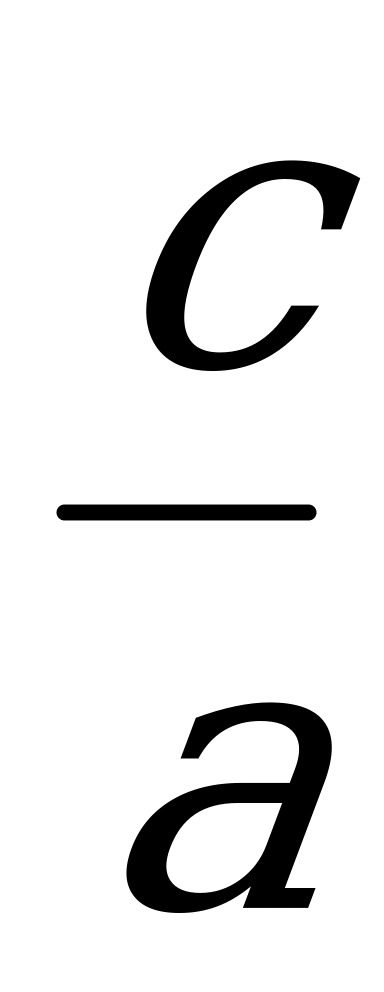 =0.
=0.
По теореме Виета х1 + х2=-
х1  х2=
х2=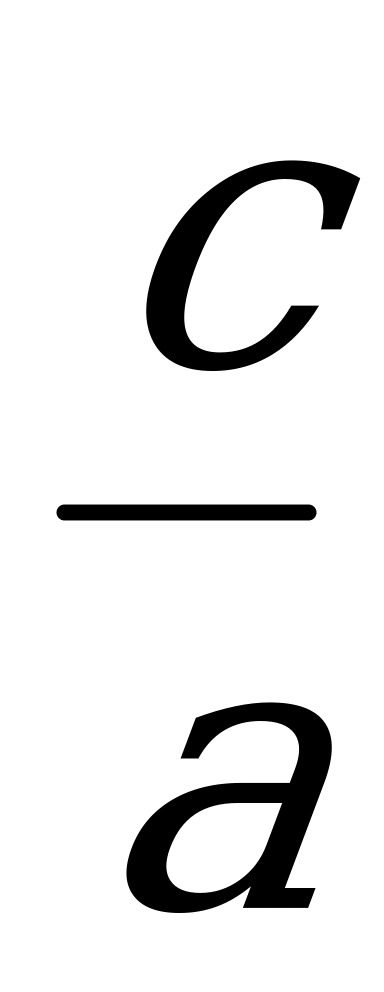
По условию a – b +c =0, откуда b= a + c.
Значит х1 + х2= -  =
= 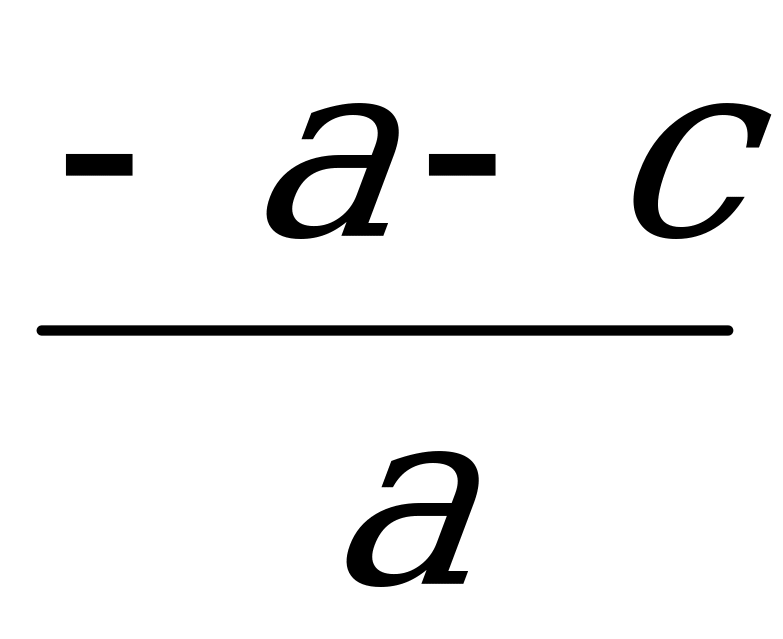 = - 1 –
= - 1 – 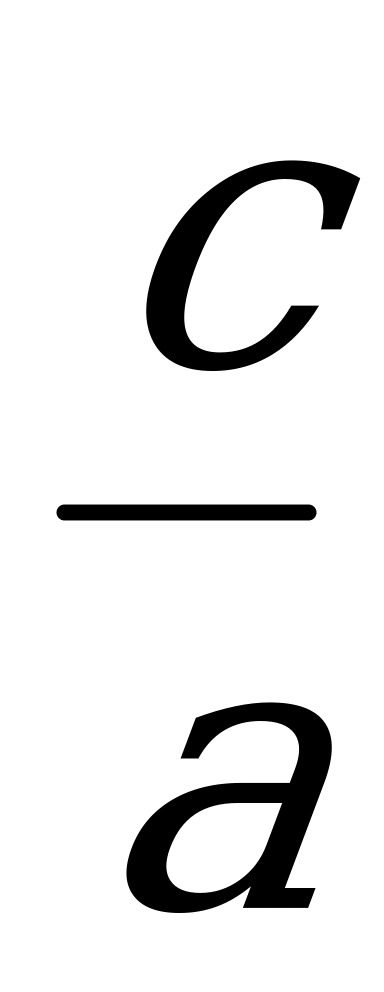 ,
,
х1  х2= - 1
х2= - 1
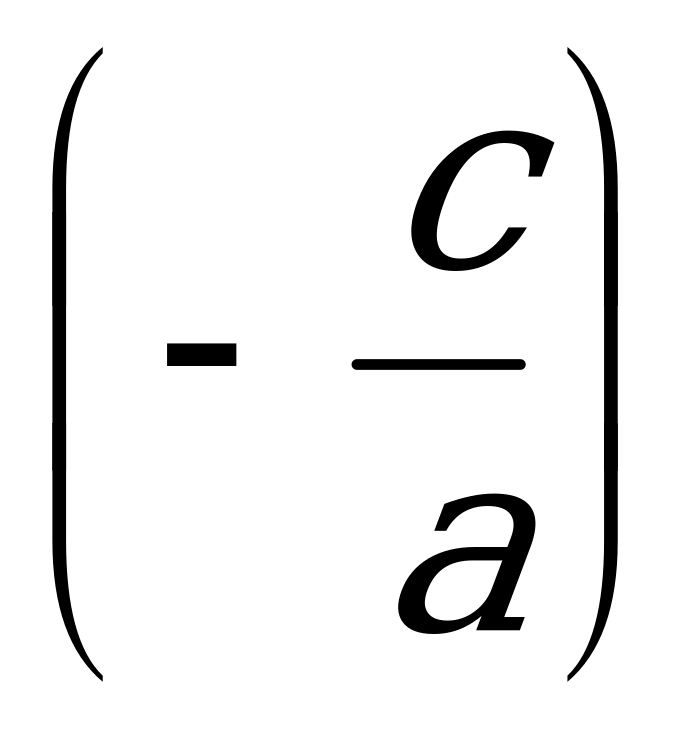
Получаем х1= - 1, х2= - 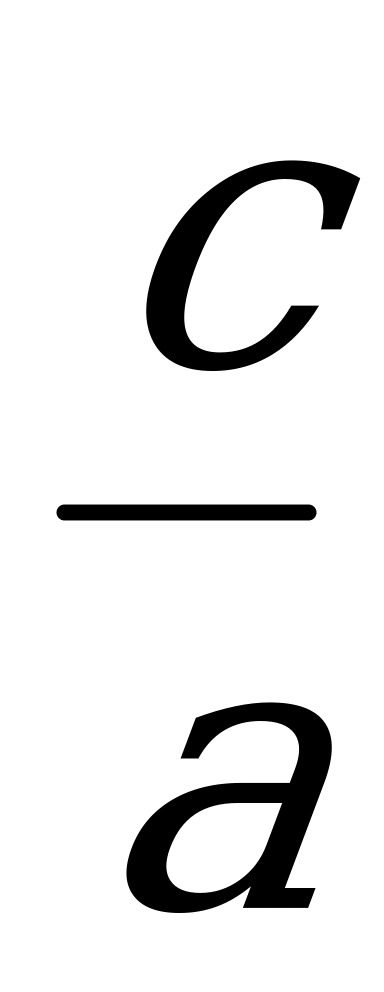 , что и требовалось доказать.
, что и требовалось доказать.
Пример. Решить уравнение: а)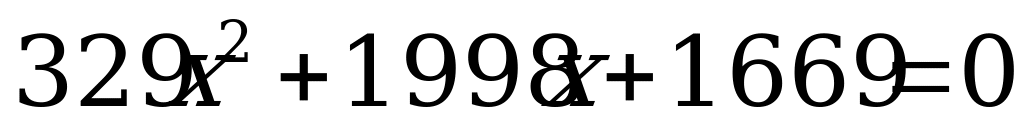
Так как 1998 = 329 + 1669, то
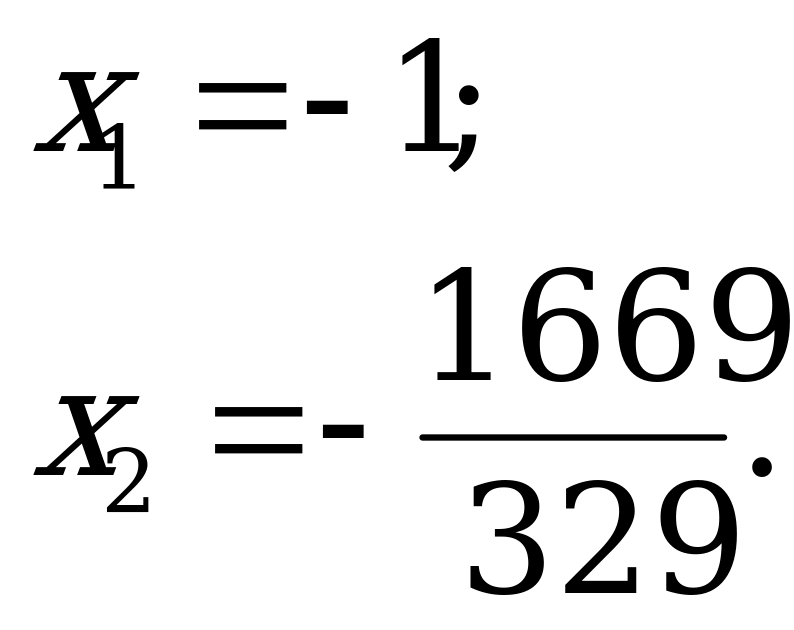
б) 10х2+2009х+1999=0
Так как 2009 = 10 + 1999, то

II ПРИЕМ ПЕРЕБРОСКИ
Используется при решении уравнений, для которых a  b + c
b + c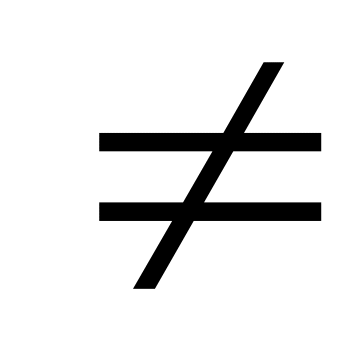 0.
0.
Например, при решении уравнения 2х2 – 11х + 5 = 0, где 2 (-11) + 5
(-11) + 5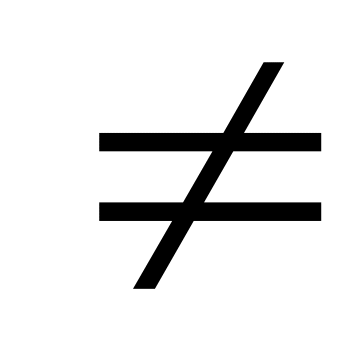 0
0
Перебросим число 2 к свободному члену, получим новое уравнение
х2 – 11х + 10 = 0, в котором 1 – 11 + 10 = 0. Следовательно, его корни 
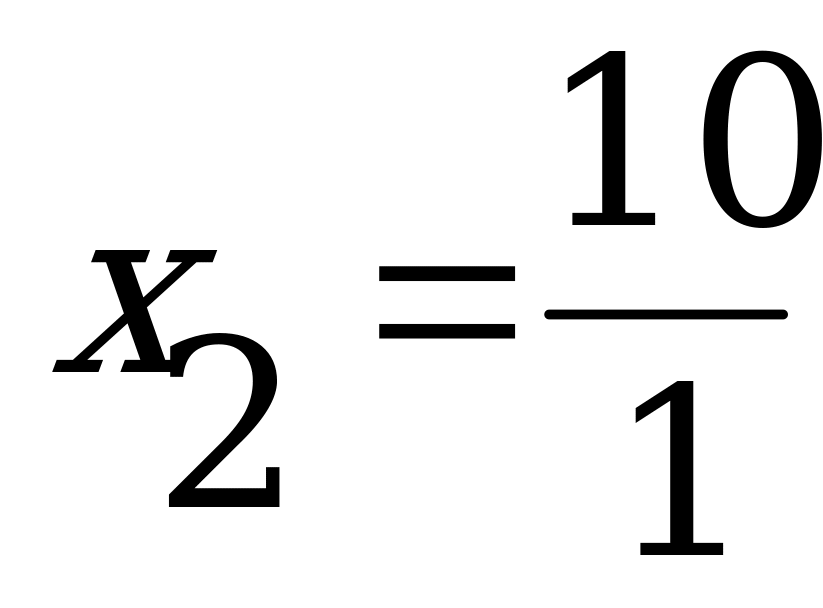 = 10. Чтобы найти корни исходного уравнения, разделим полученные значения на 2, тогда
= 10. Чтобы найти корни исходного уравнения, разделим полученные значения на 2, тогда 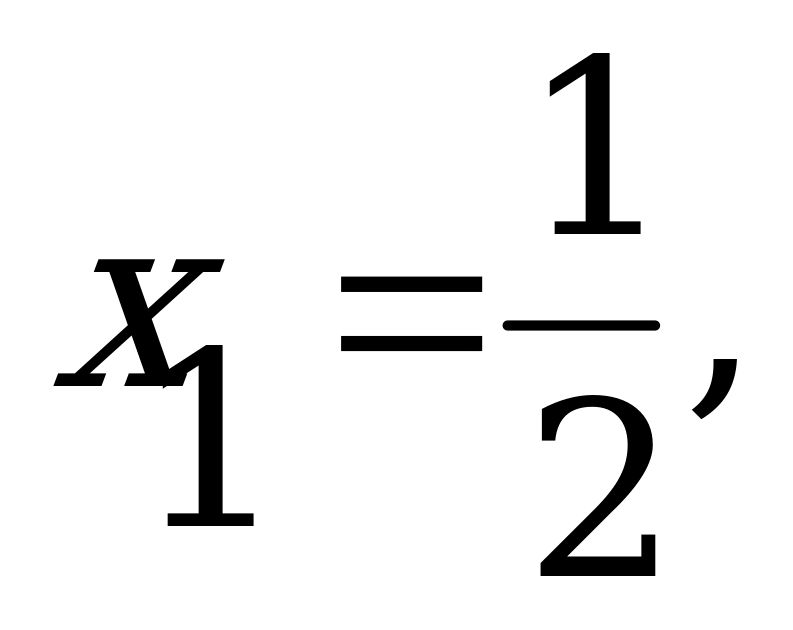
 = 5.
= 5.
Ответ: 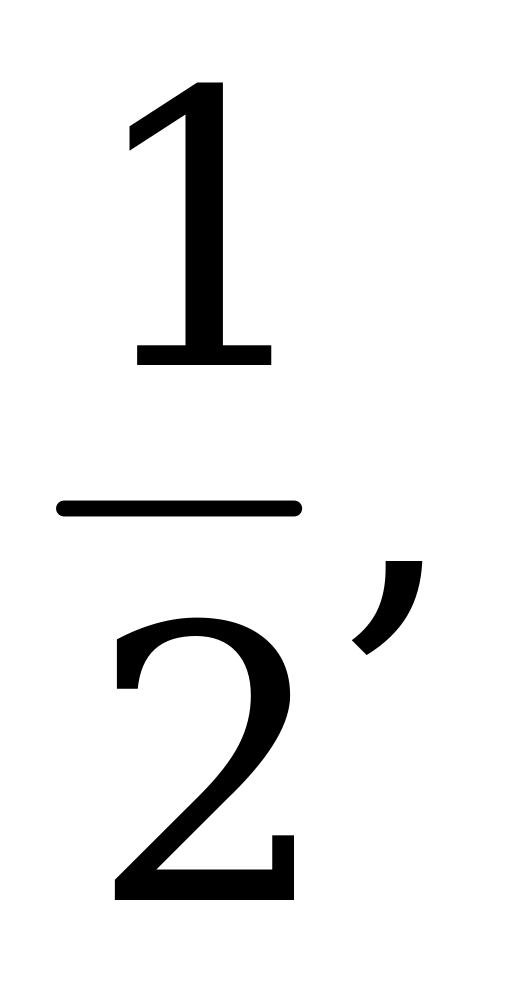 5.
5.
Этот прием можно использовать также и при решении квадратного уравнения с помощью теоремы Виета.
Пример. Решить уравнение 
Перебросим первый коэффициент


Корни 9 и (-2).
Делим числа 9 и (-2) на 6:
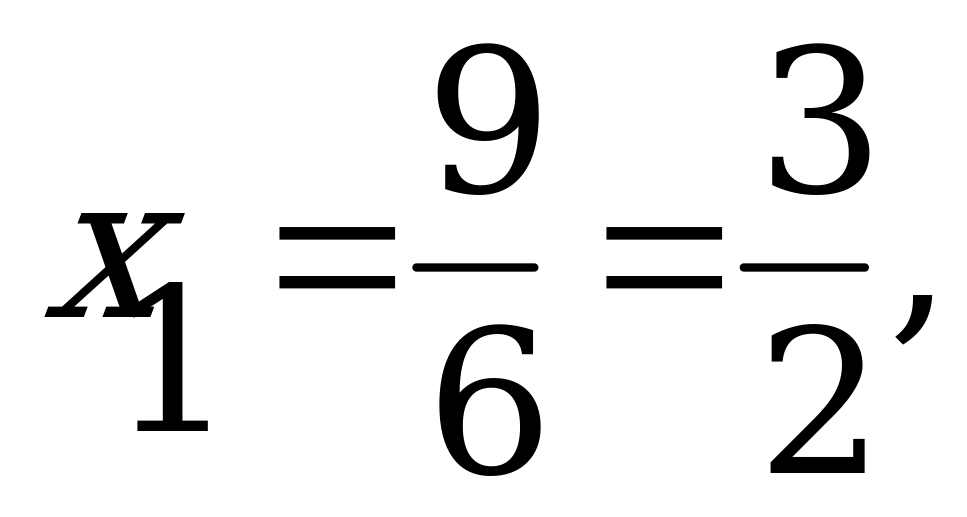
 .
.
Ответ: 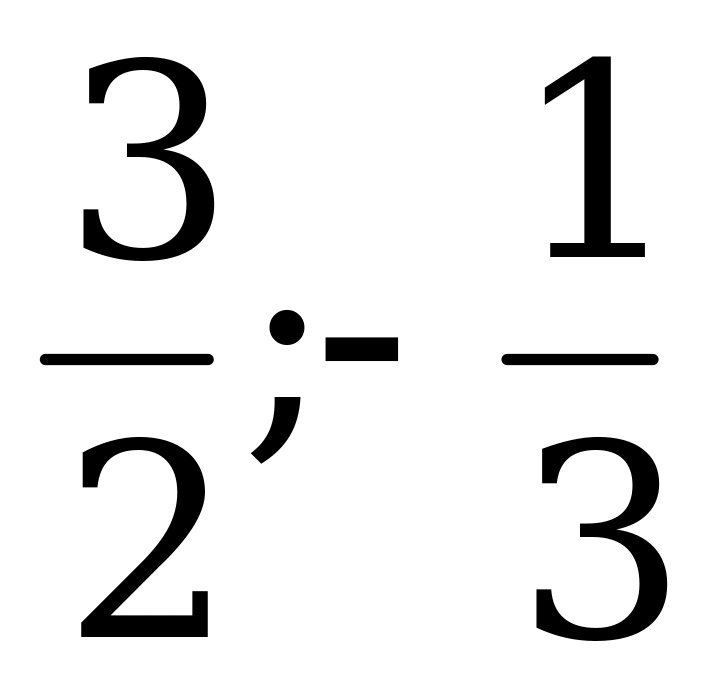
III РЕШЕНИЕ НЕКОТОРЫХ ВИДОВ КВАДРАТНЫХ УРАВНЕНИЙ
1) Уравнение вида aх2 + (а2 + 1) х + а = 0 имеет корни х1 = - а, х2 = - 
Доказательство: разделим обе части уравнения ах2 + (а2 + 1) х + а = 0 на а 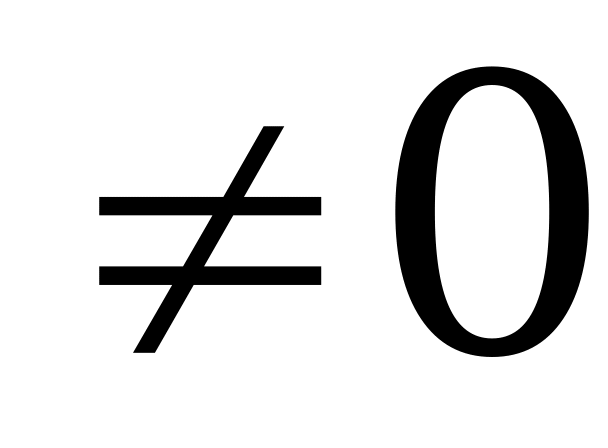 , получим приведённое квадратное уравнение x2 + (а +
, получим приведённое квадратное уравнение x2 + (а + 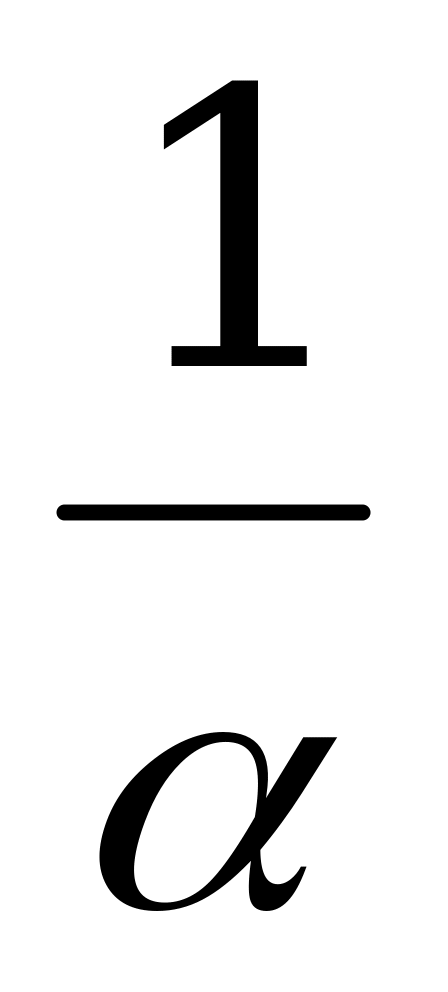 )x + 1 = 0.
)x + 1 = 0.
По теореме Виета х1 + х2 = - а – 
х1  х2= 1
х2= 1
Так как 1 = - а (
( ), то х1 = - а, х2 = -
), то х1 = - а, х2 = - 
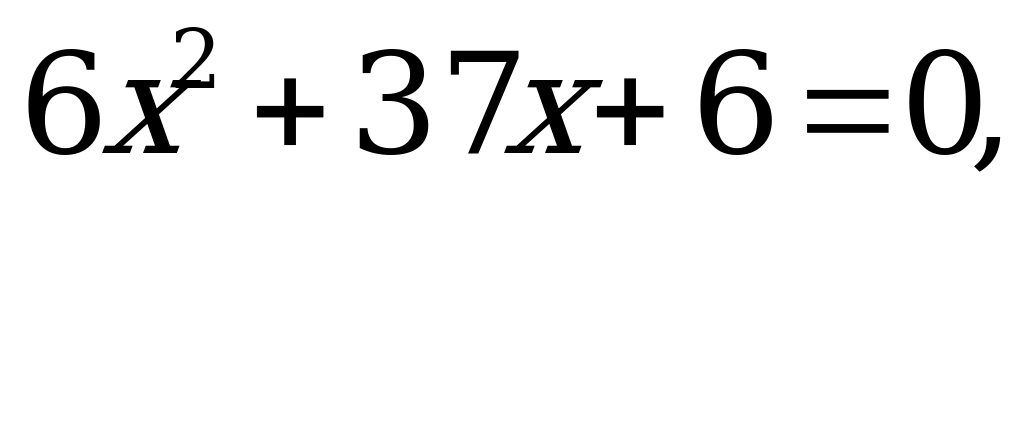
Н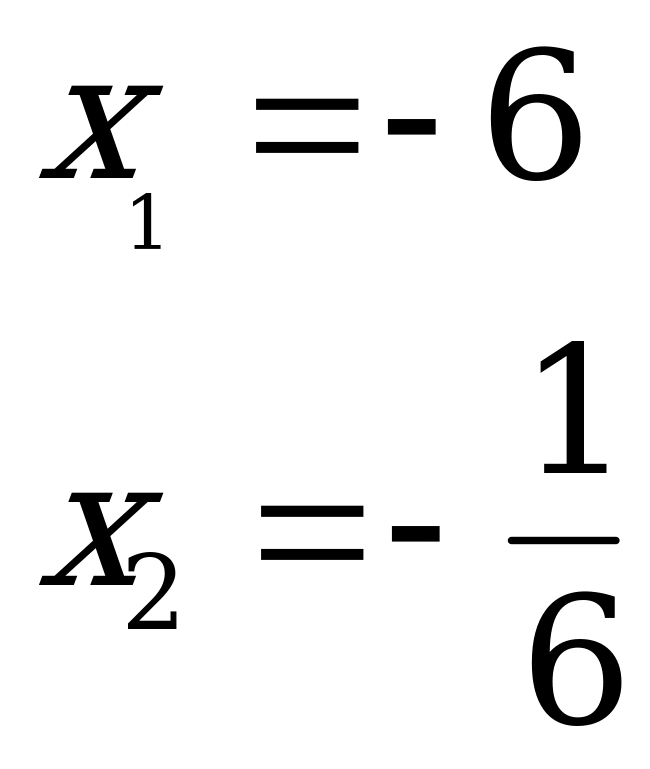 апример: то
апример: то
2) Уравнение вида ах2 – (а2 + 1) х + а = 0 имеет корни х1 = а, х2 = 
Доказательство аналогично.

Например:

3) Уравнение вида aх2 + (а2 – 1) х – а = 0 имеет корни х1 = - а, х2 = 
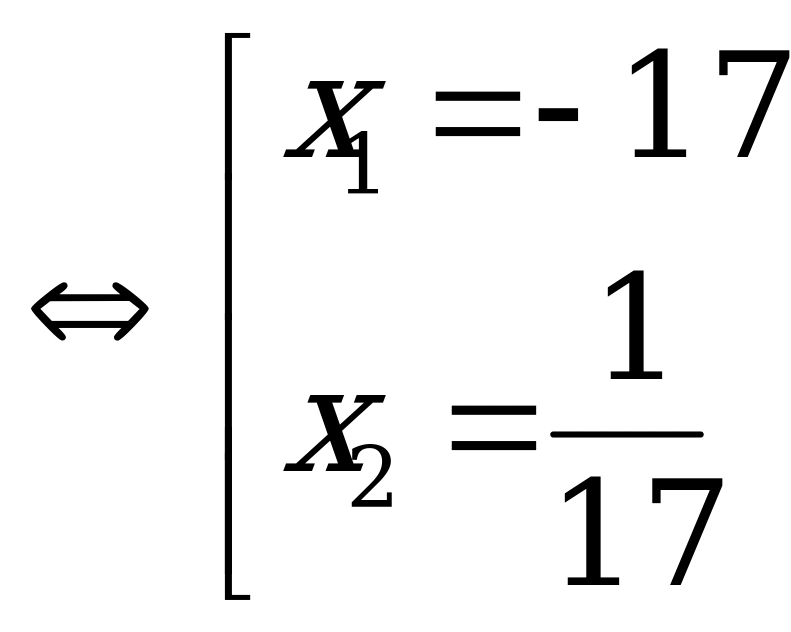
 например:
например:
4) Уравнение вида aх2 – (а2 – 1) х – а = 0 имеет корни х1 = а, х2 = - 
Н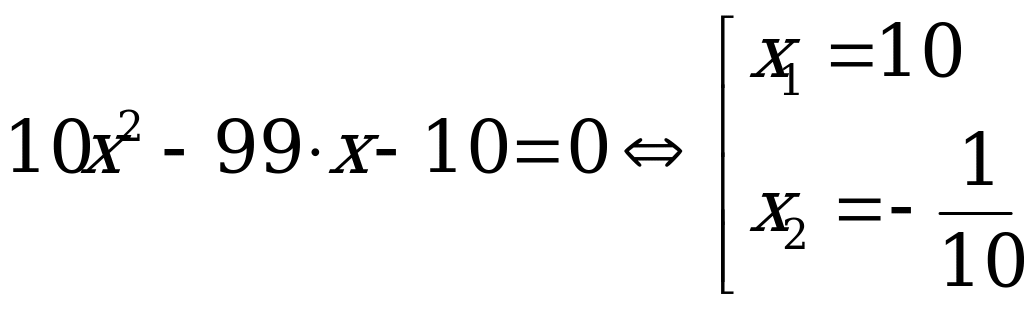 апример:
апример:
ИСПОЛЬЗОВАНИЕ ПРИЕМОВ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ
Использование теоремы, обратной теореме Виета, для составления уравнений с заданными корнями изучается в школе. Используя такие приёмы решения квадратных уравнений как прием «коэффициентов» и прием переброски, можно придумывать уравнения с рациональными корнями.
Например, составим сумму 23 – 48 + 25 = 0.
Тогда уравнение 23х2 – 48х + 25 = 0 имеет корни 1 и 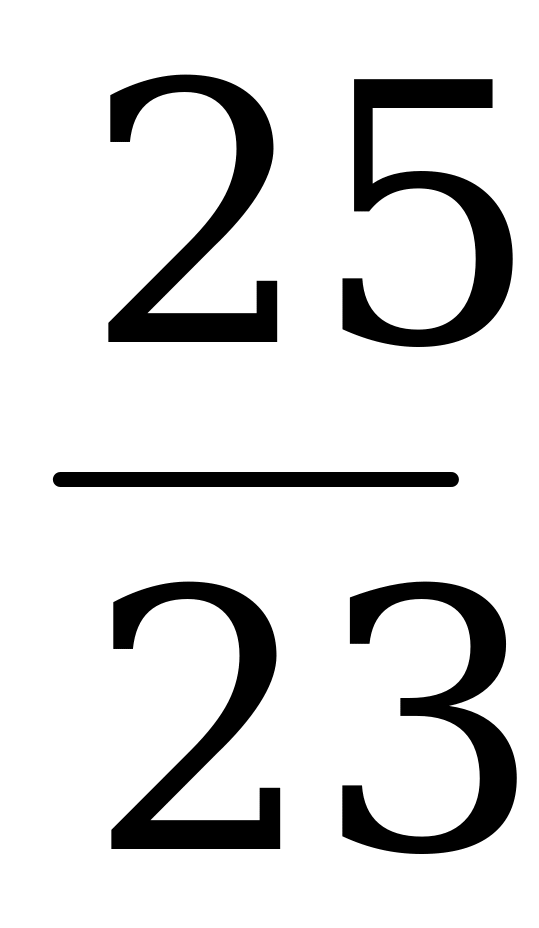 .
.
2010 = 2009 + 1  2009х2 + 2010х + 1 = 0, корни (-1) и (-
2009х2 + 2010х + 1 = 0, корни (-1) и (-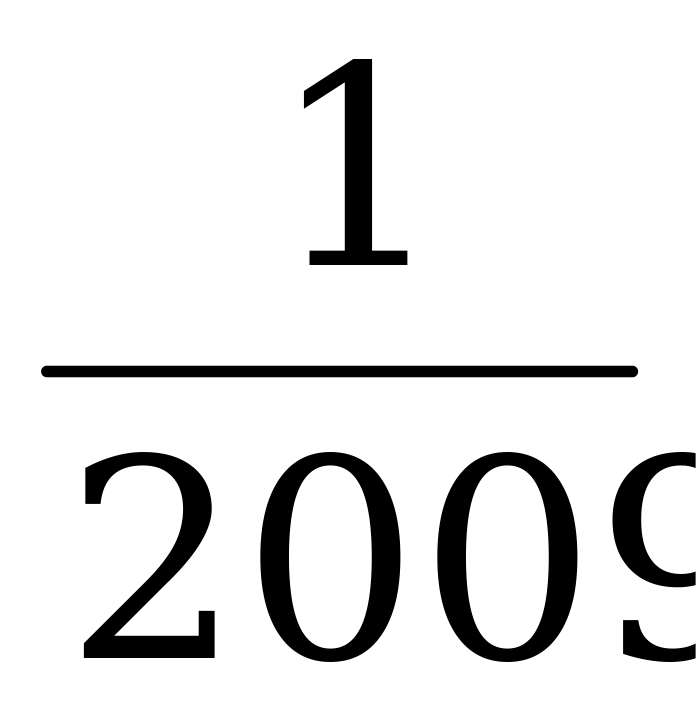 )
)
Использование приема переброски позволяет составить сразу несколько уравнений. Например, возьмём уравнение 
По теореме Виета корни 2 и 3, их произведение равно 6, 6 делится на 1,2,3,6
6=1*6
6=6*1
6=2*3
6=3*2
Используя прием переброски, можно составить еще 3 уравнения:
1)  корни
корни 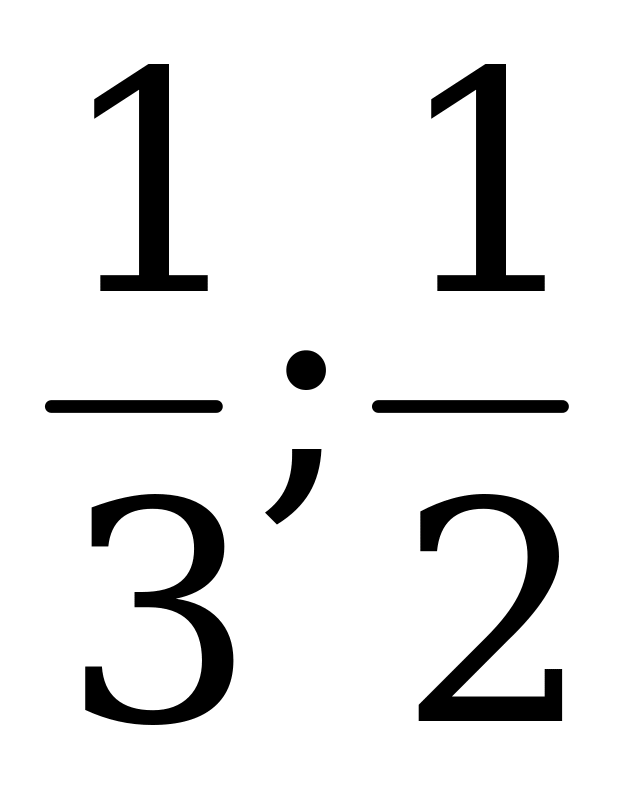
2) 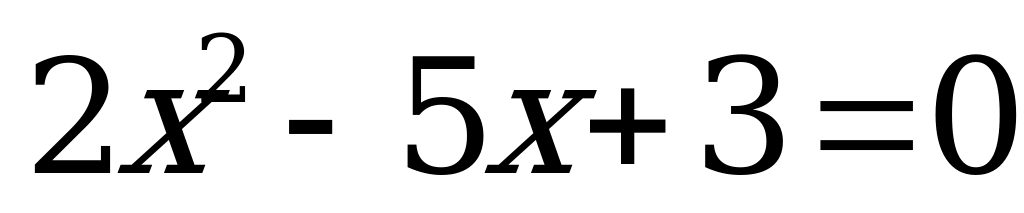 корни
корни 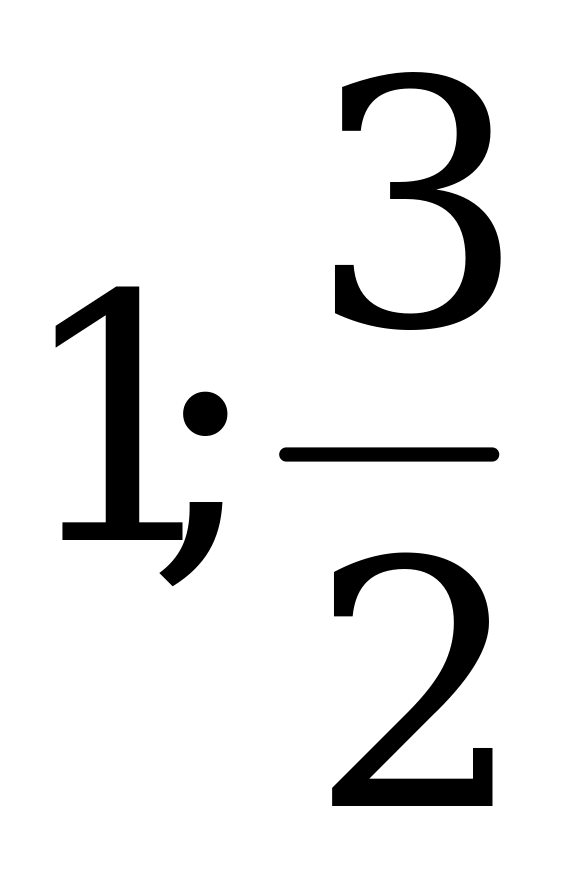
3) 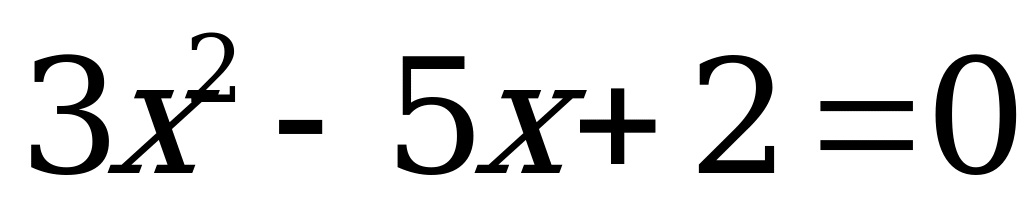 корни
корни 
ВЫВОДЫ
данные приёмы решения заслуживают внимания, поскольку они не отражены в школьных учебниках математики;
данные приёмы решения позволяют значительно сокращать вычисления, особенно при вычислении корня из дискриминанта в квадратных уравнениях с большими коэффициентами, если а и с имеют разные знаки;
овладение данными приёмами поможет экономить время и эффективно решать уравнения;
потребность в быстром решении обусловлена применением системы ЕГЭ.
ПРИЛОЖЕНИЯ
1) Решить уравнение
а)
б) 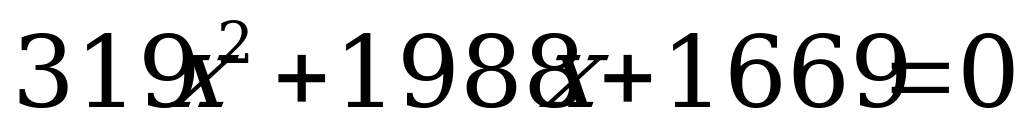
в) 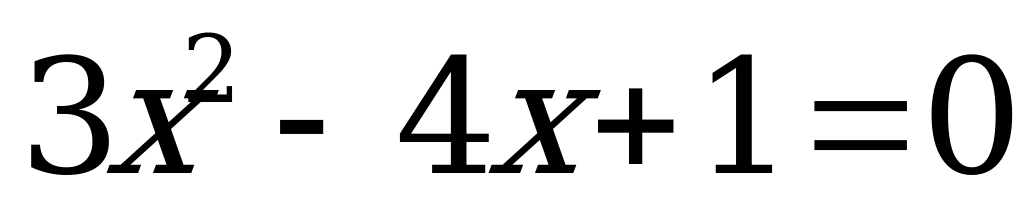
г) 
д) 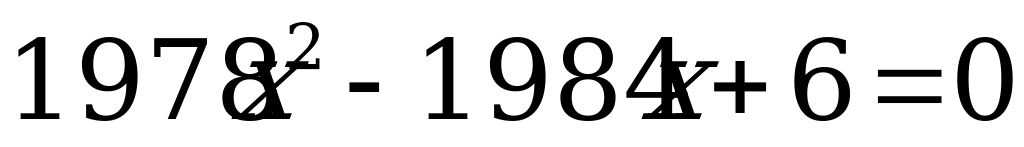
е) 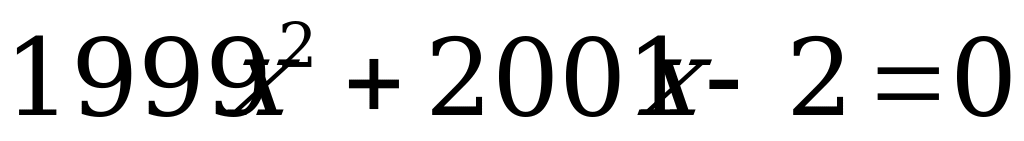
ж) 
и) 
к) 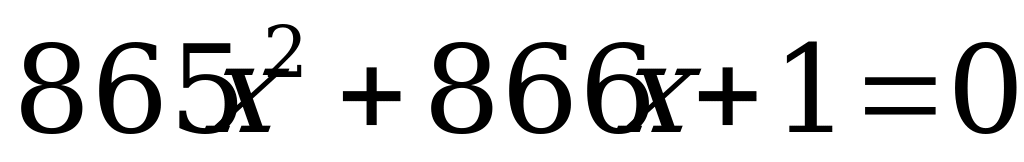
л) 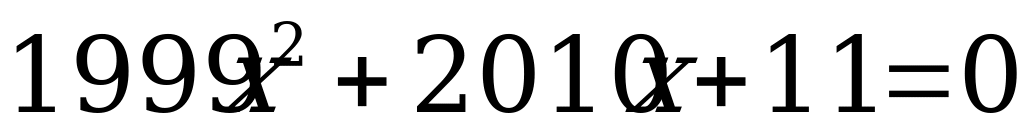
м) 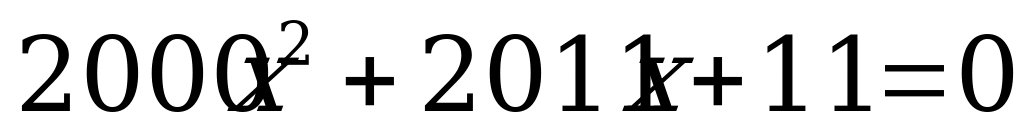
н) 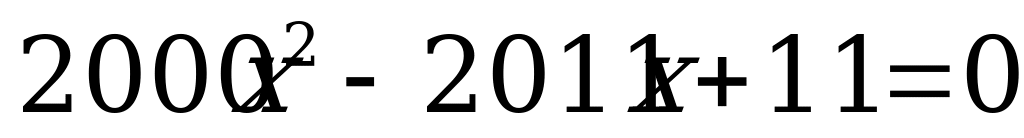
2) Составить уравнения методом переброски из уравнения х2 – 7х + 12 = 0 и найти их корни.
3) Составить уравнения методом переброски из уравнения х2 – 9х + 20 = 0 и найти их корни.
4) Составить уравнения методом переброски из уравнения х2 – 11х + 30 = 0 и найти их корни.
6) Составить уравнения методом переброски из уравнения х2 – 12х + 35 = 0 и найти их корни.
7) Решить уравнение
а) 5х2 + 26х + 5 = 0
б) 10х2 + 101х + 10 = 0
в) 5х2 – 26х + 5 = 0
г) 10х2 – 101х + 10 = 0
д) 5х2 + 24х – 5 = 0
е) 10х2 + 99х – 10 = 0
ж) 5х2 – 24х – 5 = 0
з) 10х2 – 99х – 10 = 0
8) Составить уравнение, зная его корни:
1 и 25
1 и 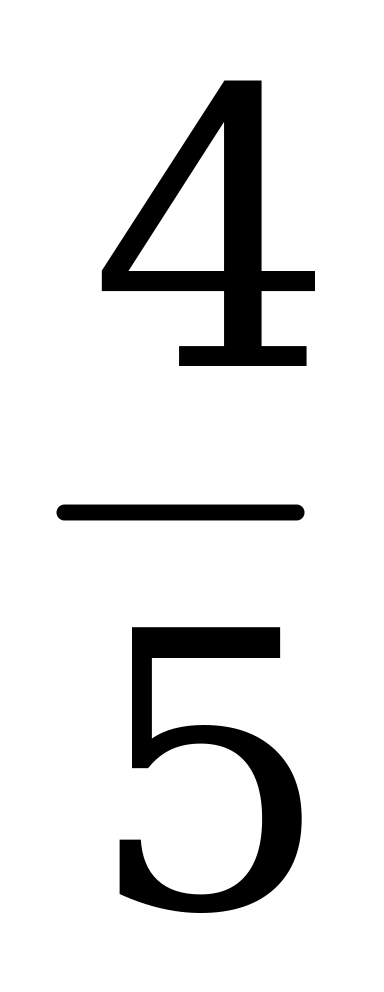
-1 и 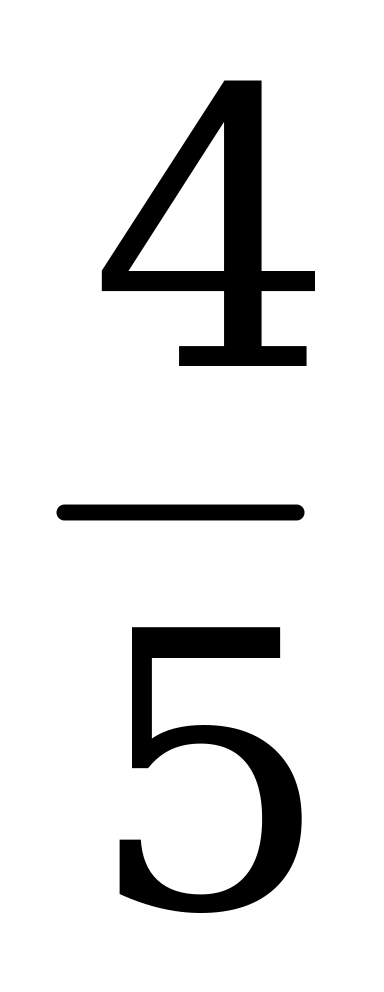
-1 и -37
1 и 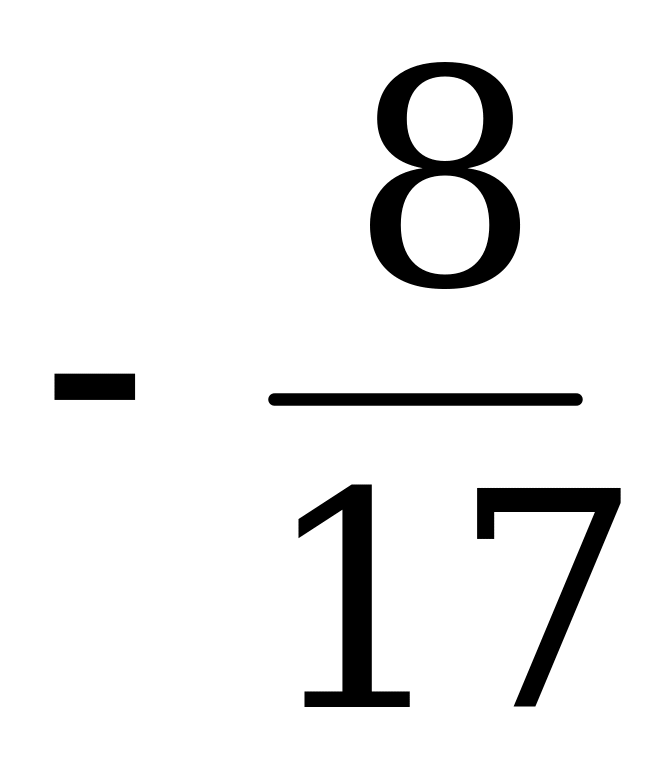
-1 и 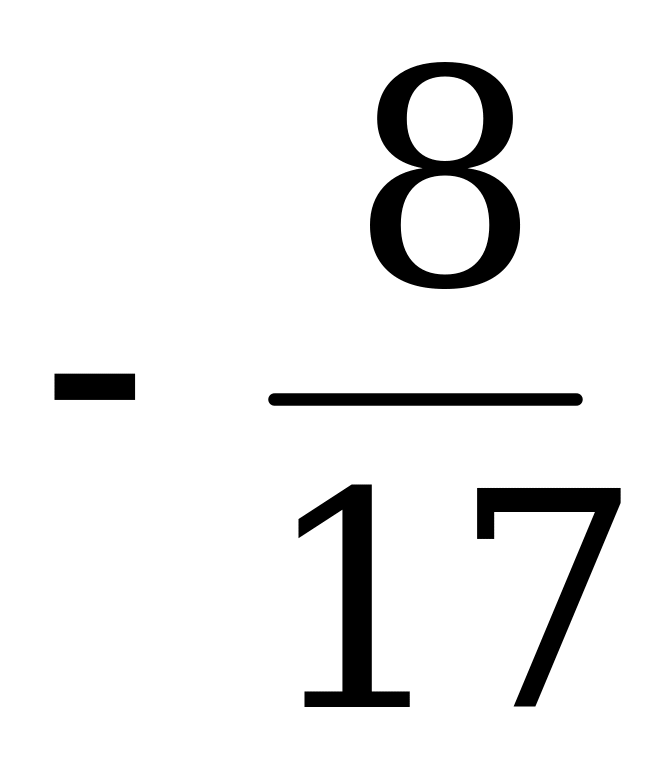
СПИСОК ЛИТЕРАТУРЫ
Ю. Н. Макарычев, Н. Г. Миндюк, К.И.Нешков, С. Б. Суворова. АЛГЕБРА, учебник для 8 класса
В.Г. Степанов. Основы исследовательской деятельности школьника. - Псков, 2004. С.34-38
Справочник по математике
Л.А.Скакунова Урок-конференция по теме «Нестандартные приемы решения квадратных уравнений Математика в школе. №6, 2008г.
http://festival.1september.ru/2005_2006/index.php?numb_artic=311026
http://center.fio.ru/som/RESOURCES/FILIPPOVMA/2002/05/KV_UR/KV_UR.HTM
http://www.iteach.ru/forum/uchproekt/m_3nqy.html?start=150
http://e-science.ru/math/theory/old/?t=143
http://festival.1september.ru/2005_2006/index.php?numb_artic=310040
http://som.fio.ru/Resources/Karpuhina/2003/12/Complited%20work/Concert/index1.htm
http://pages.marsu.ru/iac/school/s4/page74.html
http://festival.1september.ru/2004_2005/index.php?numb_artic=214032
http://lenaka.home.nov.ru/geron.htm
http://www.college.ru/mathematics/courses/stereometry/content/scientist/eukleides.html
http://portfolio.1september.ru/?p=work&id=553045
http://vio.fio.ru/vio_15/resource/HTML/Moor/P35_1/d_0.htm
11







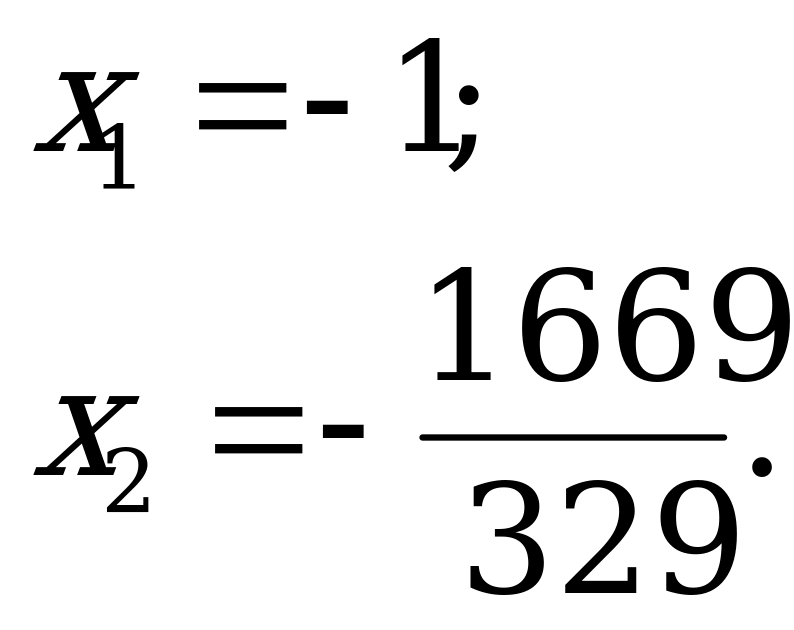

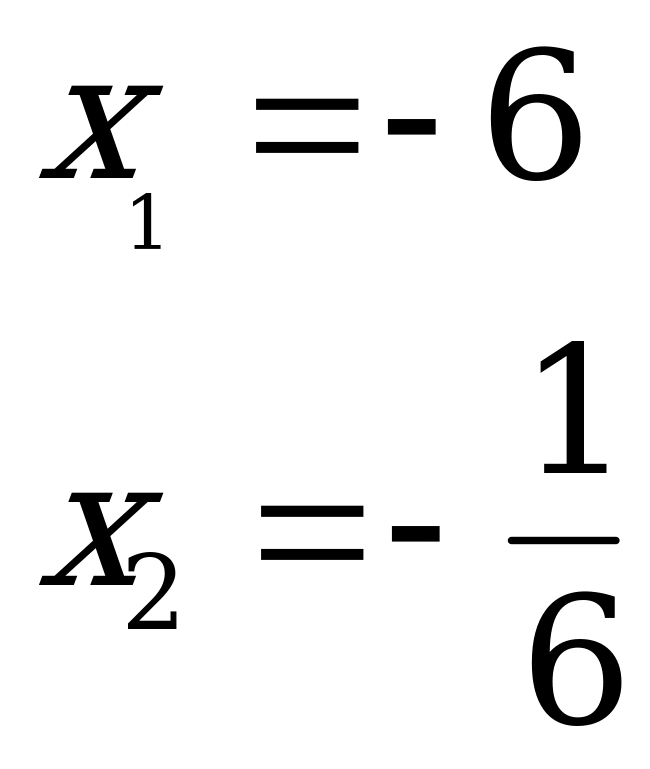 апример: то
апример: то

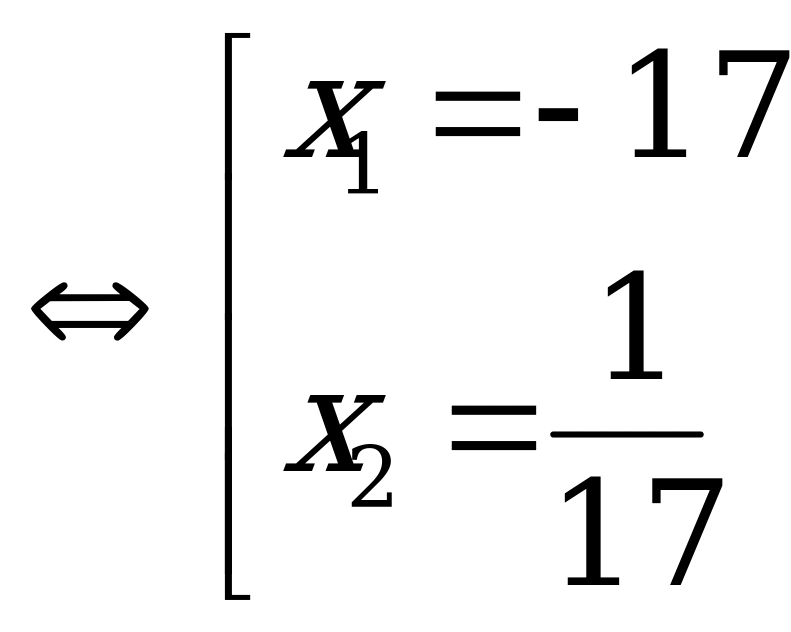
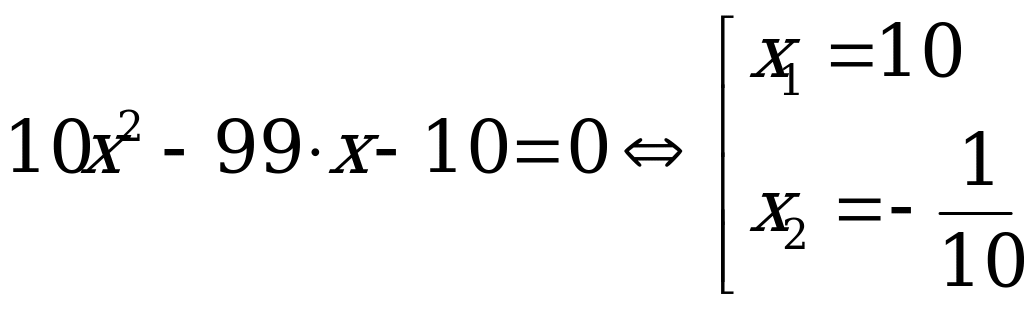 апример:
апример:
















