Министерство образования и науки
Донецкой Народной Республики
«Комсомольский индустриальный техникум»
Применение « Высшей математики»
в предметах, изучаемых студентами специальности 1302.11 « Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (по отраслям) .
Подготовила
Кулага Т.Ф.
При изучении таких дисциплин как физика, химия, начертательная геометрия, основы информатики математика является фундаментальной наукой, в других предметах специальности «ЭРГО» «математика» и «высшая математика», изучаемые в техникуме, используются неодинаково по количеству и качеству применяемых тем, разделов и понятий.
Например, для успешного изучения предмета «Начертательная геометрия» учащиеся должны:
Усвоить понятия:
а) правильных многоугольников;
б) многоугольников, вписанных в окружность;
в) взаимного расположения двух прямых;
г) взаимного пересечения поверхностей многогранников и круглых тел и сечение их плоскостями;
д) кривых второго порядка;
е) диаграмм и графиков;
ж) о геометрических телах и методах их получения.
II. Уметь:
1) вписывать в окружность правильные треугольник, четырехугольник, шестиугольник, восьмиугольник и т.д.
2) строить графики прямой и обратной пропорциональности, эллипса, гиперболы, параболы.
3) строить сечения круглых тел плоскостями.
4) строить сечения многогранников плоскостями.
5) строить фигуры, центрально – симметричные данной.
6) строить параллельные и ортогональные проекции.
7) делить угол и отрезок на 2, 3 и т.д. равных частей.
III. Знать методы приближенного вычисления.
Уметь применять микрокалькуляторы.
При изучении физики студенты должны иметь понятие и приближенных числах и вычислениях с заранее заданной точностью, о приращении функции и аргументов, о подобии треугольников, о прямой и обратной пропорциональности, зависимости и их графиках, о тригонометрических функциях и их графиках, о снижении колебаний, о векторах, об осях и системе координат, о геометрических телах, их поверхностях, о объемах.
Информатику можно считать разделом математики, так они тесно связаны.
В химии применяются приближенные вычисления, прямая обратная пропорциональные зависимости, степенная, показательная функции, линейные уравнения, сводимые к линейным, неравенства, геометрические тела, их поверхности и объемы.
В некоторых предметах, например «Горное дело», «Рудничный транспорт», «Горные машины» применяются только расчеты по формулам, графики функций, приближенные вычисления, таблицы и диаграммы, в других предметах, например «Открытая разработка месторождений полезных ископаемых» кроме выше перечисленных понятий применяются формулы тригонометрии, на конкретных примерах где и как они применяются будет указано в дальнейшем изложении. В предмете «Общая электротехника тригонометрия применяется еще больше. Но кроме этих тем используется понятие комплексных чисел и ряды Фурье.
Применение комплексных чисел
в расчете физических величин
Так как комплексные числа геометрически представляются векторами на плоскости, то все векторные физические величины могут быть охарактеризованы при помощи комплексных чисел. Представление векторных физических величин комплексными числами облегчает выполнение расчетов этих величин. При этом действия над векторами, которые выполняются графическим путем, заменяются соответствующими действиями над комплексными числами, которые выполняются аналитически, что значительно проще. Кроме того, комплексные числа могут быть взяты в алгебраической, тригонометрической и показательной формах в зависимости от конкретного случая. Особенно широкое применение комплексные числа получили в электротехнике при расчете электрических цепей. В электротехнике мнимая единица і обозначается буквой j , т.к. буквой і традиционно обозначается сила тока в цепи.
 y M
y M
U1
 600
600

O 900 x
U2
N
Рассмотрим один пример. На рисунке одна векторная диаграмма неразветвленной цепи переменного тока. Пусть вектор 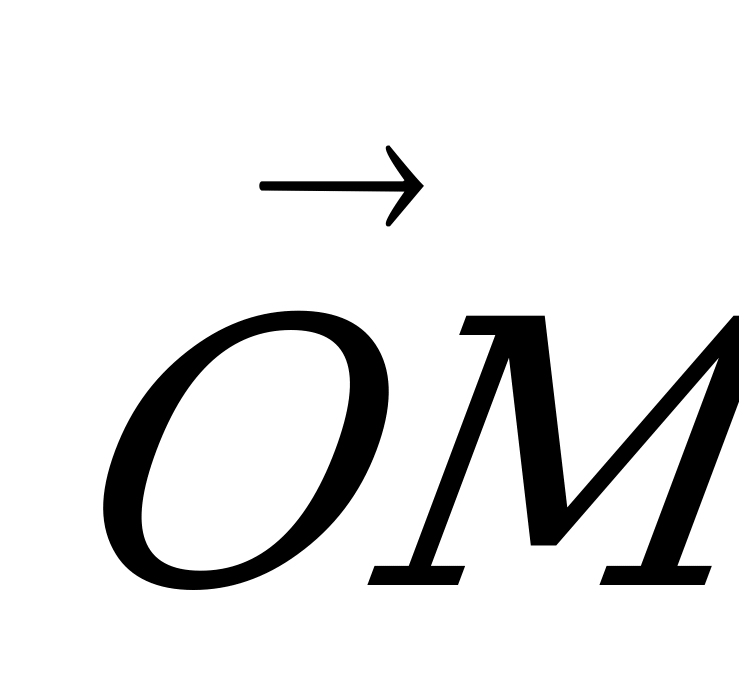 представляет вектор напряжения
представляет вектор напряжения 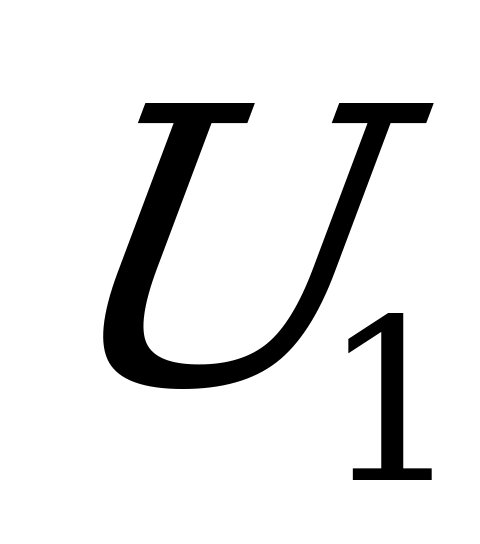 , модуль которого
, модуль которого 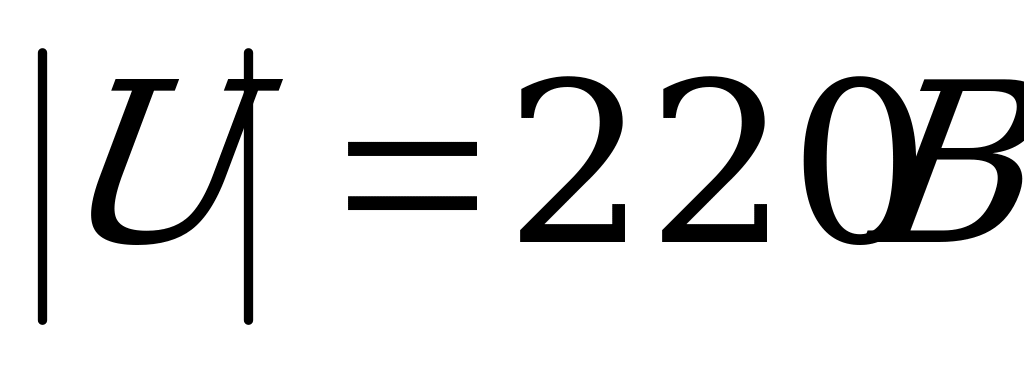 . Вектор
. Вектор 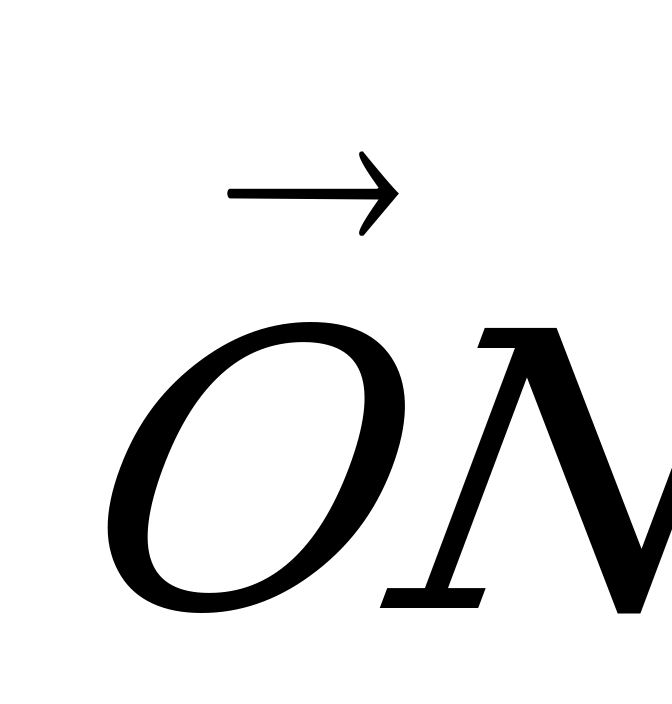 представляет вектор напряжения
представляет вектор напряжения 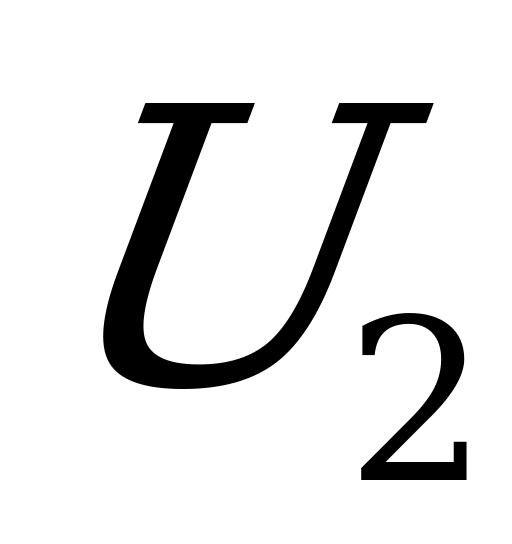 , модуль которого
, модуль которого 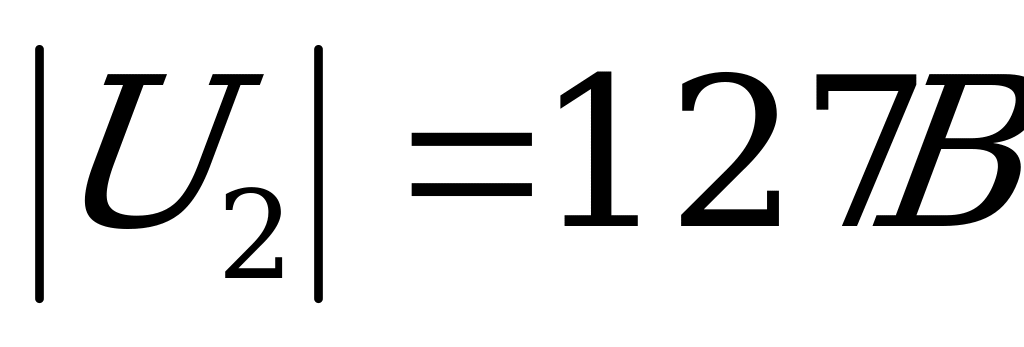 .
.
Тогда: U1=220(cos 600+j sin 600)=110+190,5j .
Также: U2=220(cos (-90)0+j sin(- 900))= -127j.
Если электрическая цепь составлена из двух последовательно включенных участков с напряжением 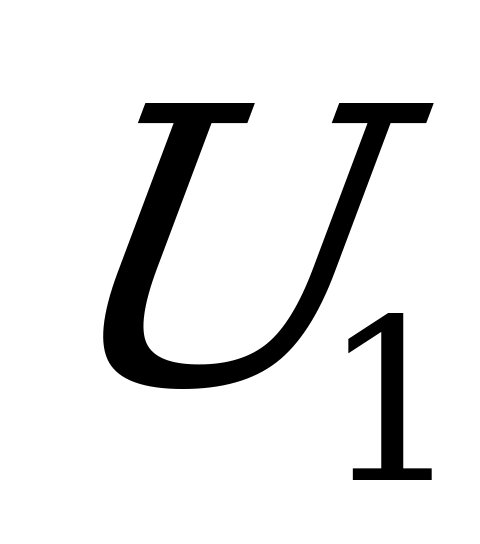 и
и 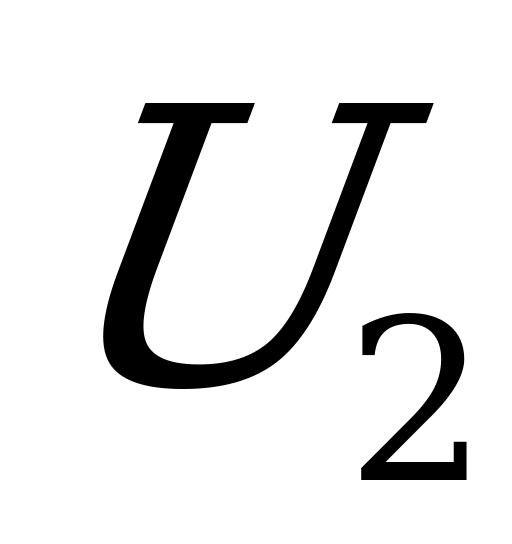 , то на зажимах будем иметь напряжение:
, то на зажимах будем иметь напряжение:
U=U1+U2=110+190,5j -127j=110+63,5j.
При включении цепи на постоянное напряжение в процессе увеличения тока в катушке будет индуктироваться э.д.с. самоиндукции 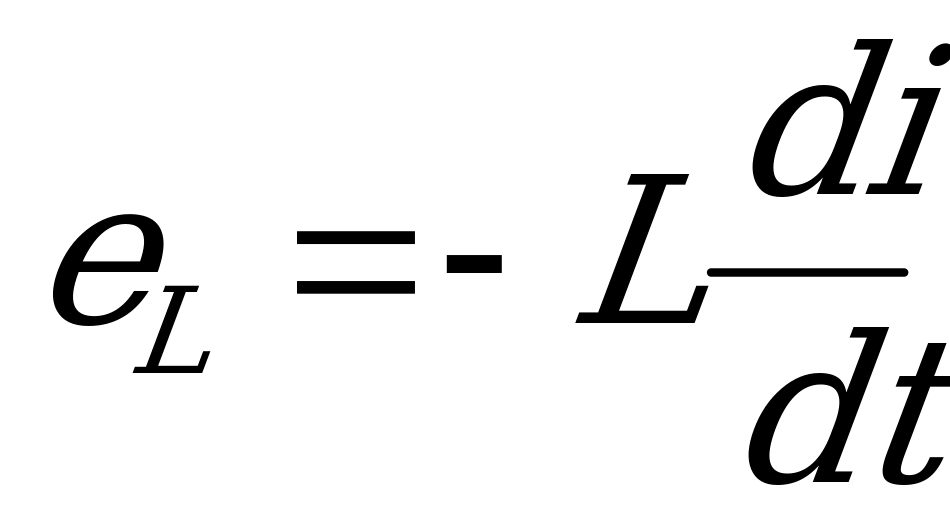 . Применив второй закон Кирхгофа, напишем:
. Применив второй закон Кирхгофа, напишем:
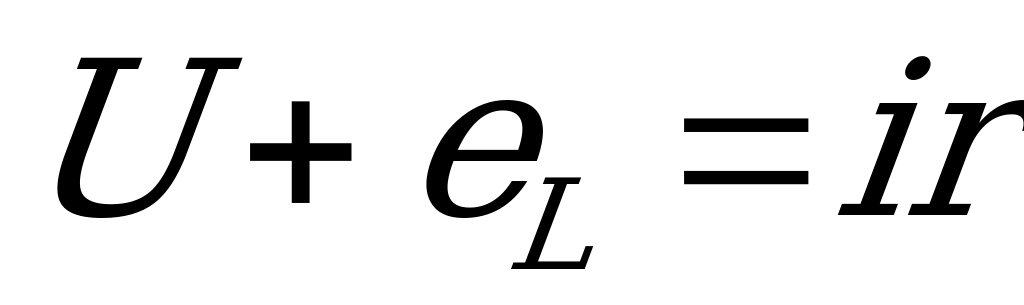
откуда 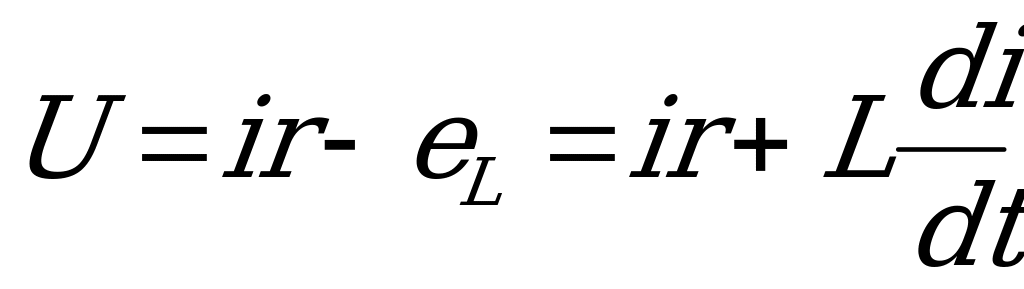 .
.
Таким образом, напряжение на зажимах цепи состоит из двух слагающих. Первая слагающая напряжения 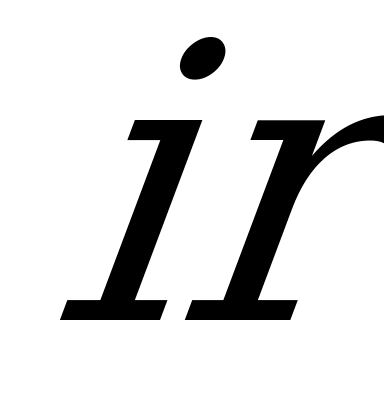 определяется по закону Ома. Вторая слагающая напряжения
определяется по закону Ома. Вторая слагающая напряжения 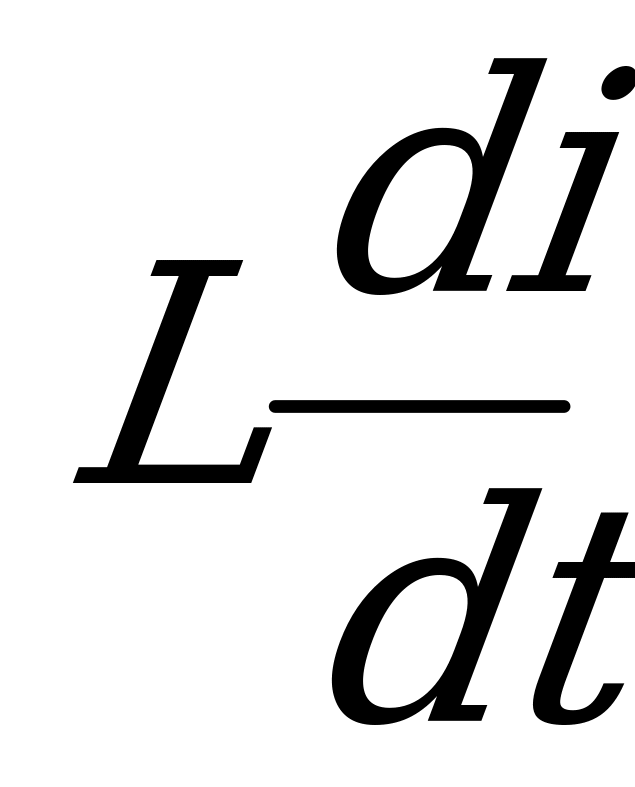 равна по величине и противоположна по направлению
равна по величине и противоположна по направлению 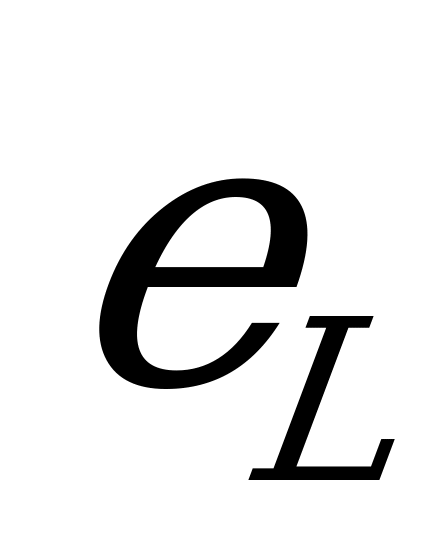 ; она уравновешивает возникающую в цеп э.д.с. самоиндукции.
; она уравновешивает возникающую в цеп э.д.с. самоиндукции.
Умножив обе части уравнения на произведение 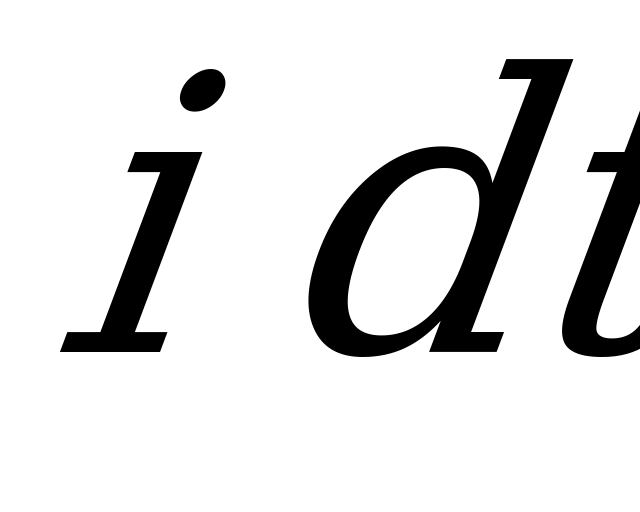 , получим:
, получим:
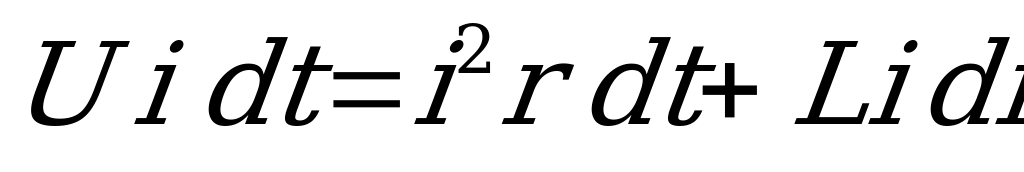 .
.
Левая часть этого уравнения выражает собой энергию, полученную цепью за время  , правая часть того же уравнения показывает, что часть энергии
, правая часть того же уравнения показывает, что часть энергии 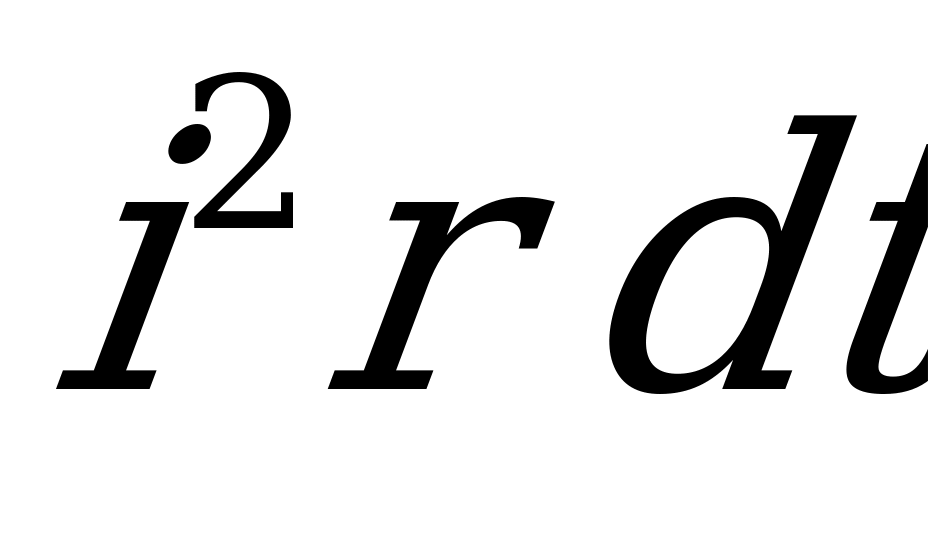 расходуется на нагревание проводов цепи, другая же часть полученной энергии
расходуется на нагревание проводов цепи, другая же часть полученной энергии 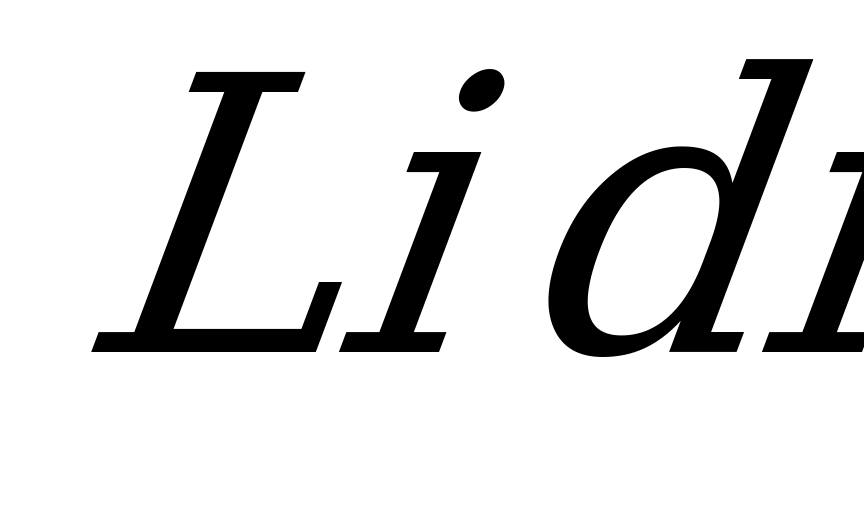 запасается в магнитном поле цепи.
запасается в магнитном поле цепи.
Суммируя приращение энергии при увеличении тока от нуля до значения 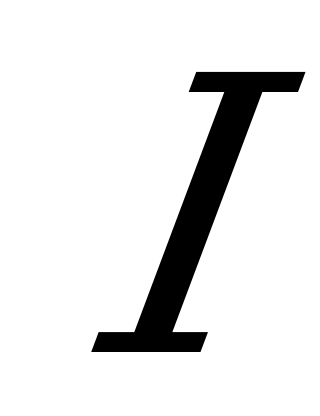 , получим энергию, запасенную в магнитном поле цепи:
, получим энергию, запасенную в магнитном поле цепи:
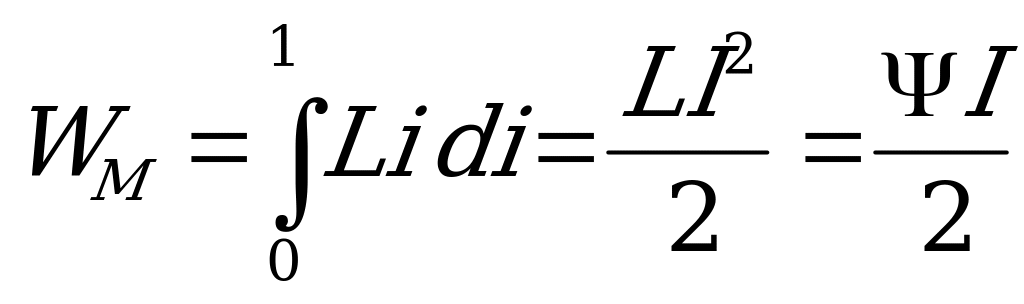 .
.
Высшая математика в теме по электротехнике
«Действующие значения тока и напряжения»
При расчете цепей переменного тока обычно пользуются понятием действующих (эффективных) значений переменного тока, напряжения и э.д.с.
Действующие значения тока, напряжения и э.д.с. обозначаются прописными буквами 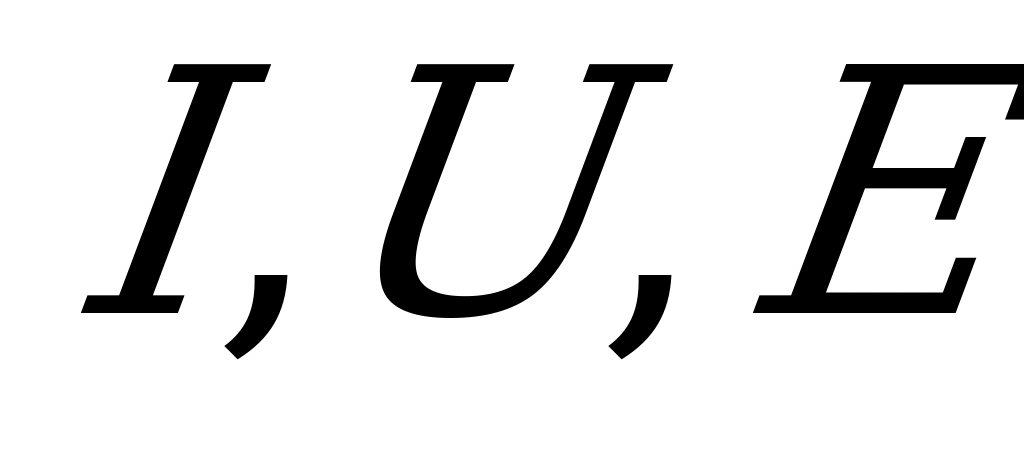 .
.
На шкалах измерительных приборов и технической документации также указываются действующие значения величин.
Действующее значение переменного тока равно значению такого эквивалентного постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет в нем за период то же количество тепла.
Количество тепла, выделенное переменным током в сопротивлении 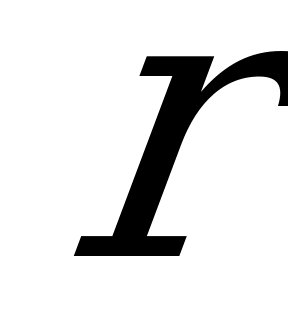 за бесконечно малый промежуток времени
за бесконечно малый промежуток времени
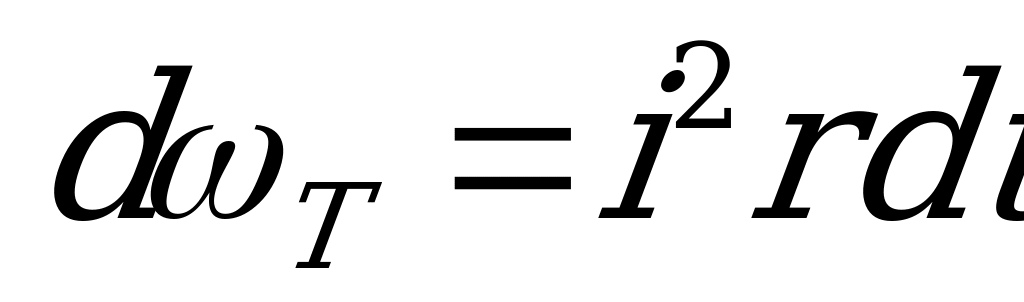 ,
,
а за период переменного тока 
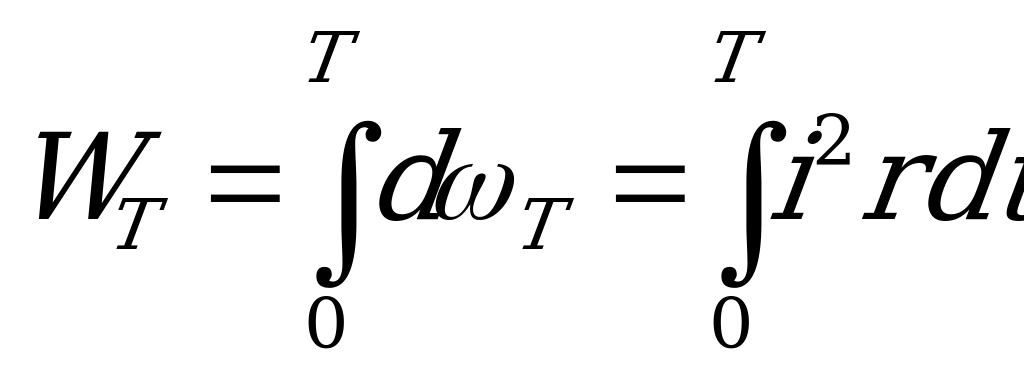 .
.
Приравняв полученное выражение 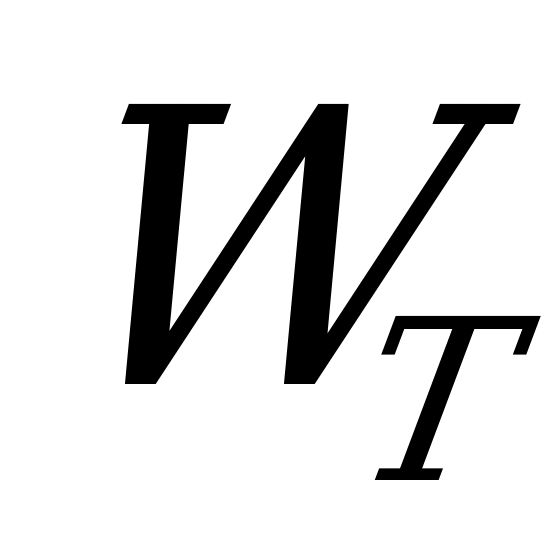 количеству тепла
количеству тепла 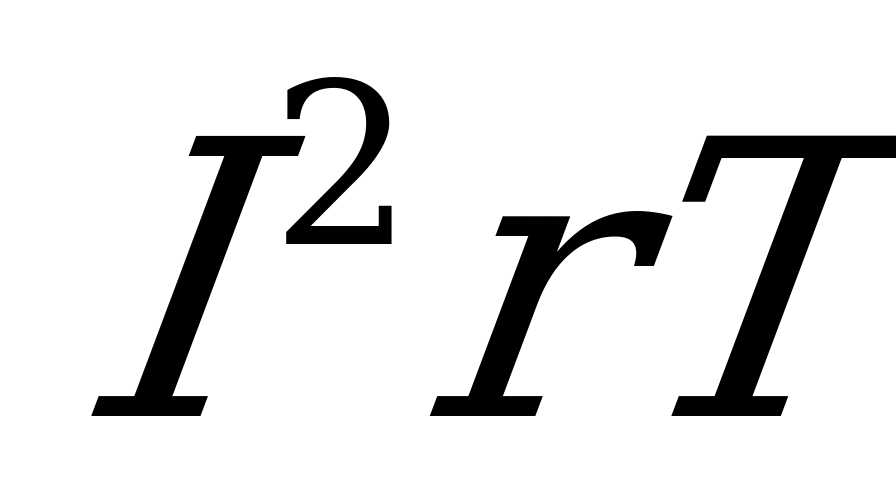 , выделенному в том же сопротивлении
, выделенному в том же сопротивлении 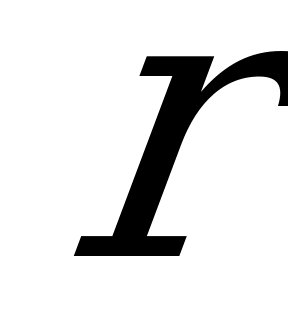 постоянным током
постоянным током 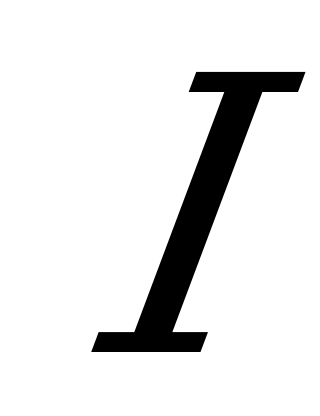 за то же время
за то же время  , получим :
, получим :
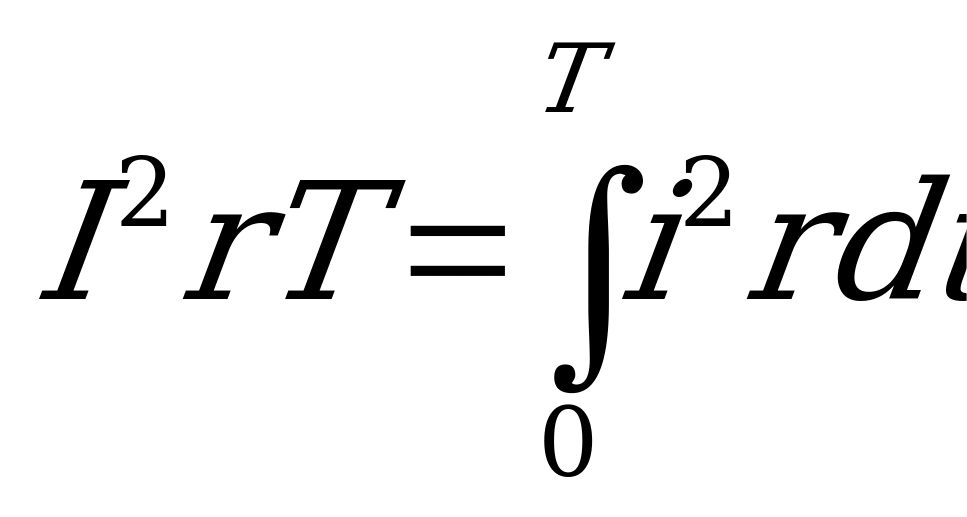 .
.
Сократив общий множитель 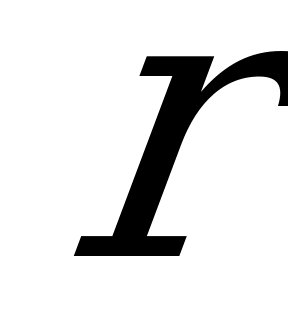 , получим действующее значение тока
, получим действующее значение тока
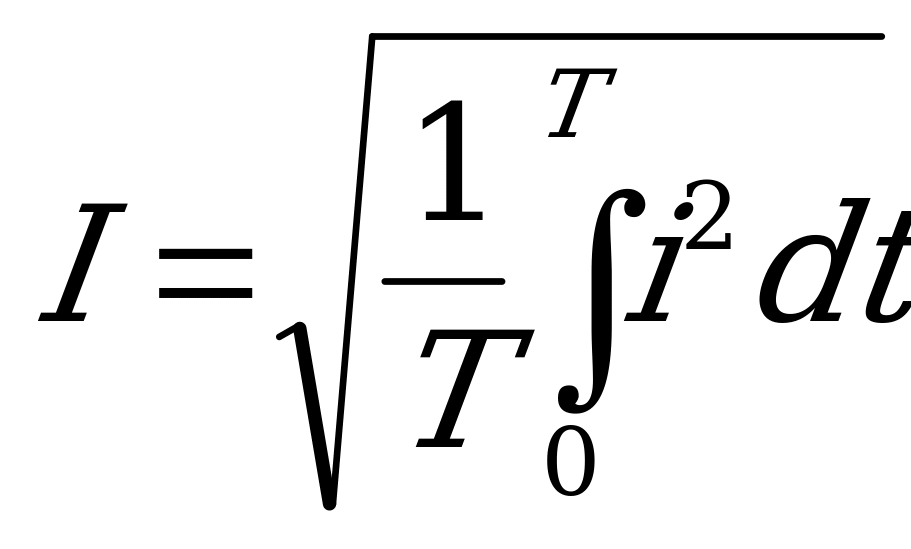 .
.
На рисунке построена кривая мгновенных значений тока 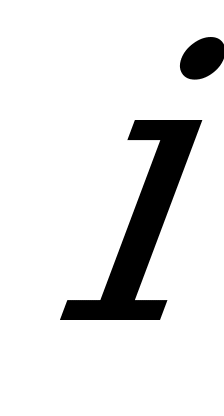 и кривая квадратов мгновенных значений
и кривая квадратов мгновенных значений 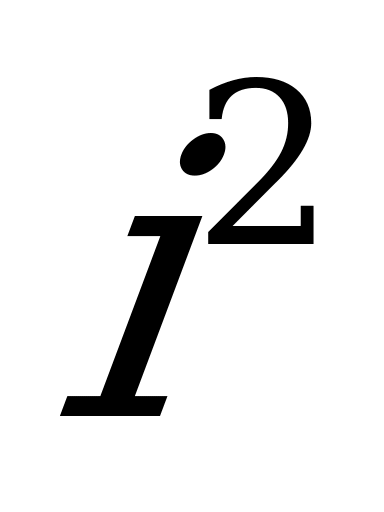 . Площадь, ограниченная последней кривой (
. Площадь, ограниченная последней кривой (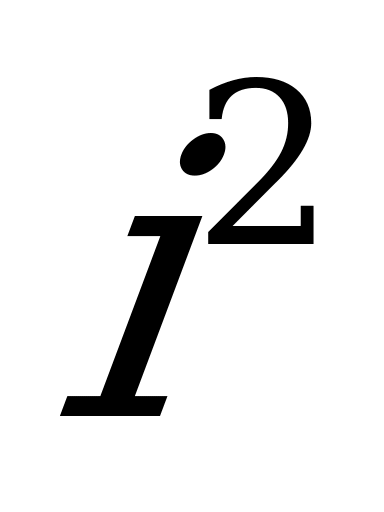 ) и осью абсцисс, представляет собой в некотором масштабе величину, определяемую выражением
) и осью абсцисс, представляет собой в некотором масштабе величину, определяемую выражением 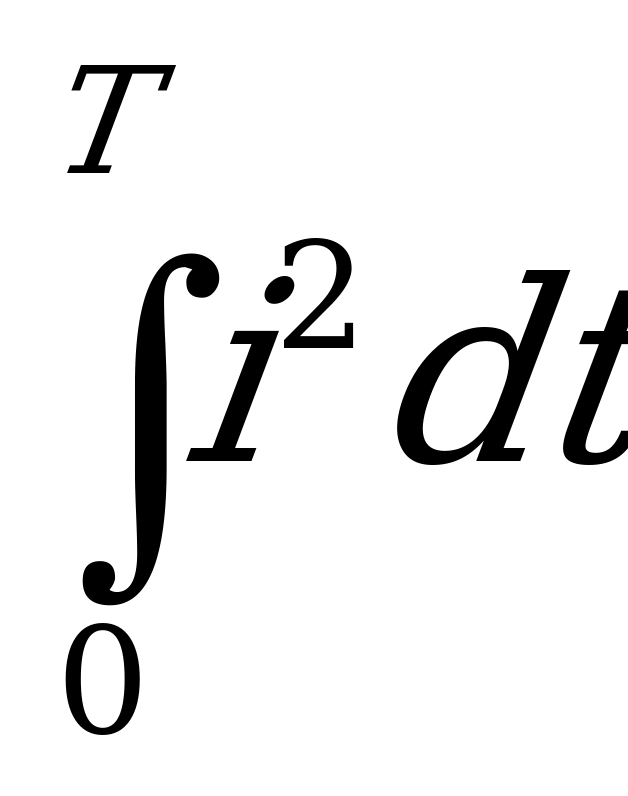 . Высота Аб прямоугольника АбвДА, равновеликого площади, ограниченной кривой
. Высота Аб прямоугольника АбвДА, равновеликого площади, ограниченной кривой 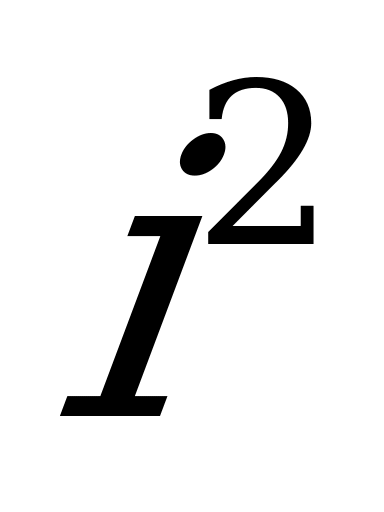 и осью абсцисс, равная среднему значению ординат кривой
и осью абсцисс, равная среднему значению ординат кривой 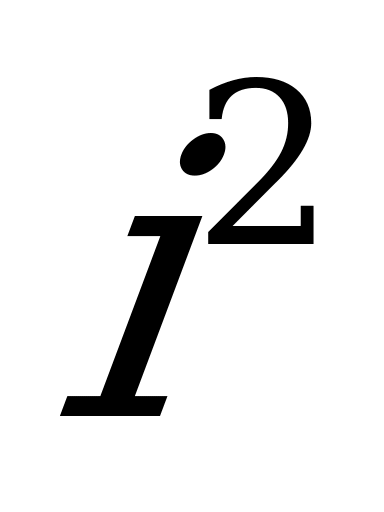 , представляет собой квадрат действующего значения тока
, представляет собой квадрат действующего значения тока 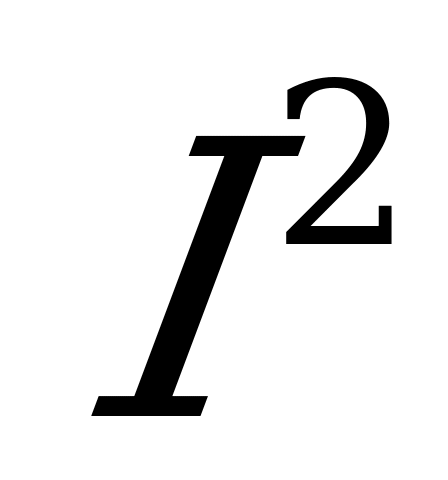 .
.
График переменного тока и квадрата тока.
Если ток изменяется по закону синуса, т.е.
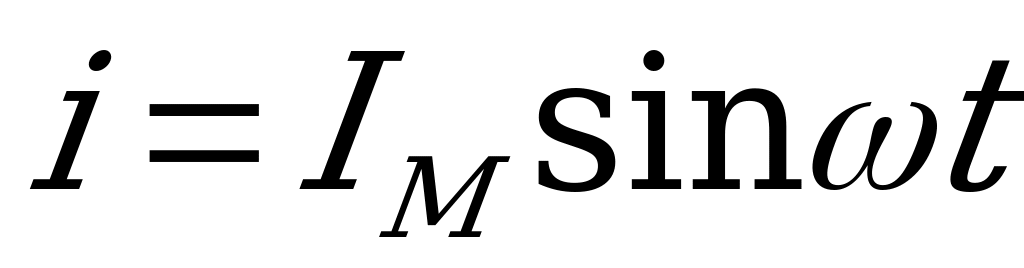 ,
,
то 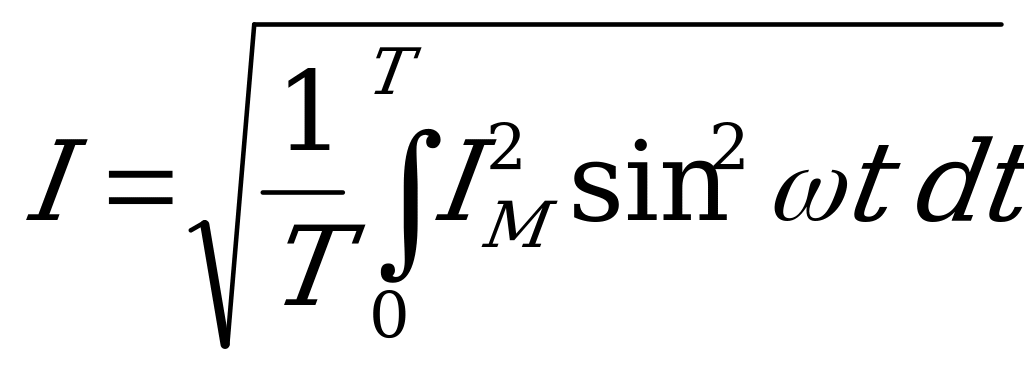 .
.
Так как
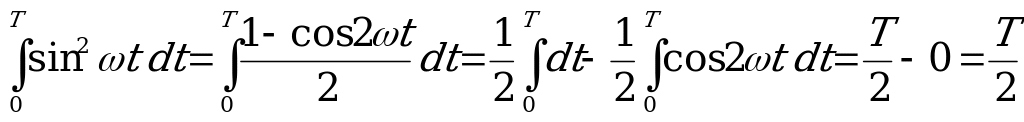 ,
,
то 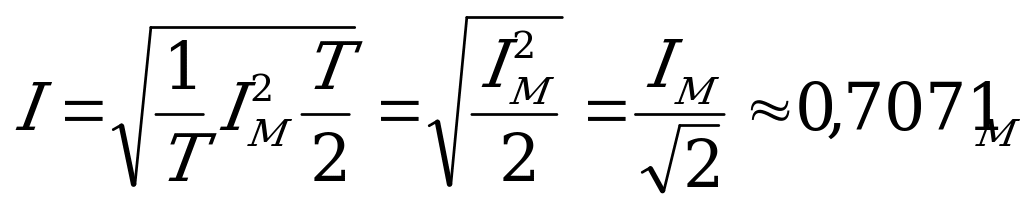 .
.
Аналогично для действующих значений синусоидальных напряжений и э.д.с. можно записать:
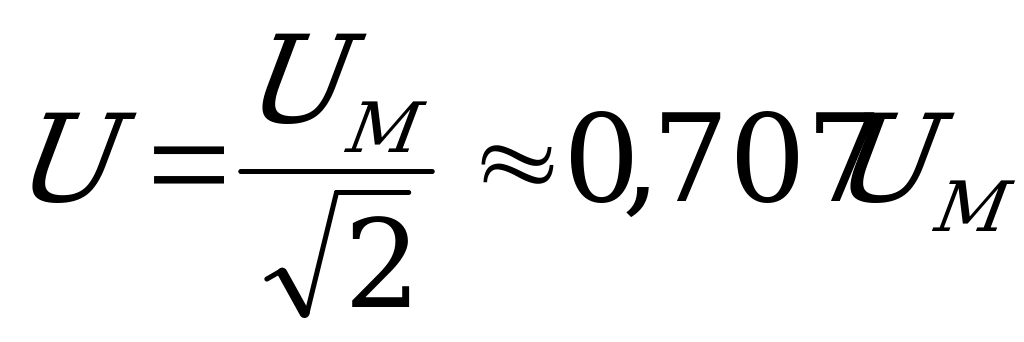 и
и 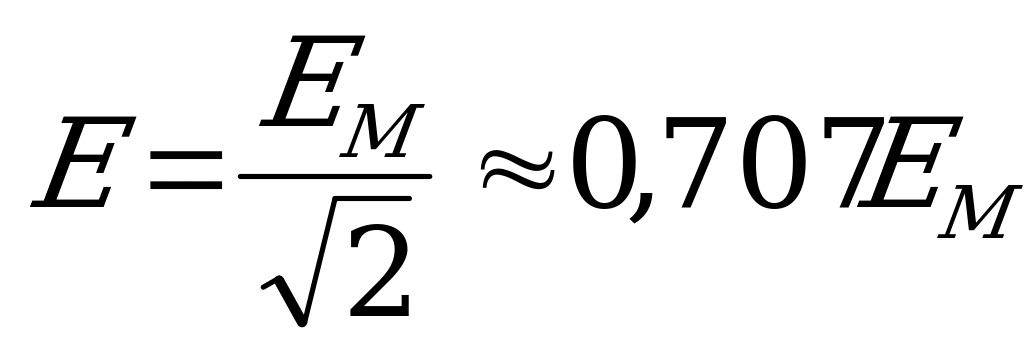 .
.
Кроме действующего значения тока и напряжения, иногда пользуются еще понятием среднего значения тока и напряжения.
Среднее значение синусоидального тока за период равно нулю, так как в течение первой половины периода определенное количество электричества  проходит через поперечное сечение проводника в прямом направлении. В течение второй половины периода то же количество электричества проходит через сечение проводника в обратном направлении. Следовательно, количество электричества, прошедшее через сечение проводника за период, равно нулю, равно нулю и среднее за период значение синусоидального тока.
проходит через поперечное сечение проводника в прямом направлении. В течение второй половины периода то же количество электричества проходит через сечение проводника в обратном направлении. Следовательно, количество электричества, прошедшее через сечение проводника за период, равно нулю, равно нулю и среднее за период значение синусоидального тока.
Поэтому среднее значение синусоидального тока 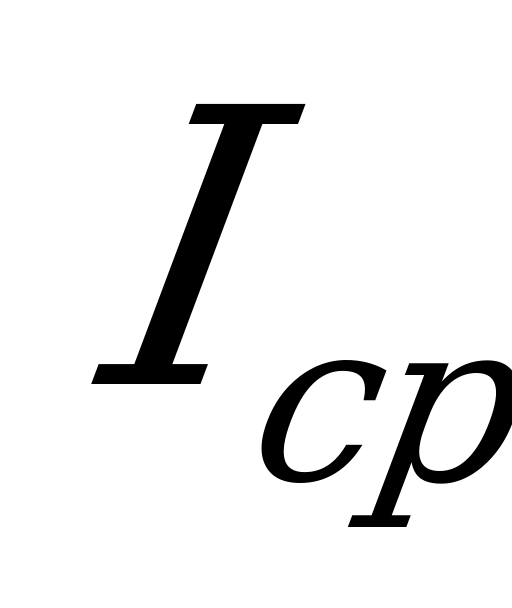 вычисляют за полупериод, в течение которого ток остается положительным. Среднее значение тока равно отношению количества электричества, прошедшего через сечение проводника за половину периода, к продолжительности этого полупериода. Таким образом,
вычисляют за полупериод, в течение которого ток остается положительным. Среднее значение тока равно отношению количества электричества, прошедшего через сечение проводника за половину периода, к продолжительности этого полупериода. Таким образом,
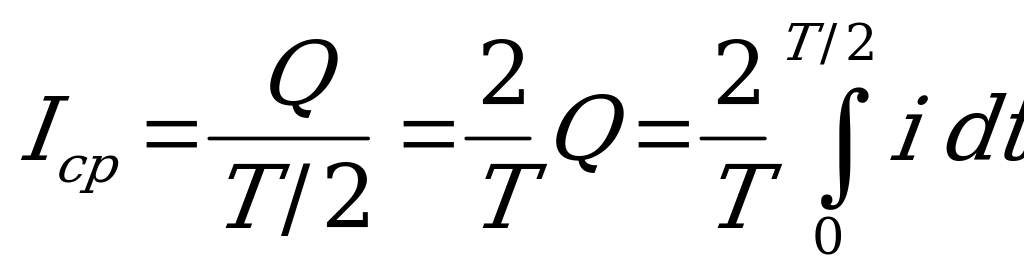 ,
,
причем начало отсчета времени 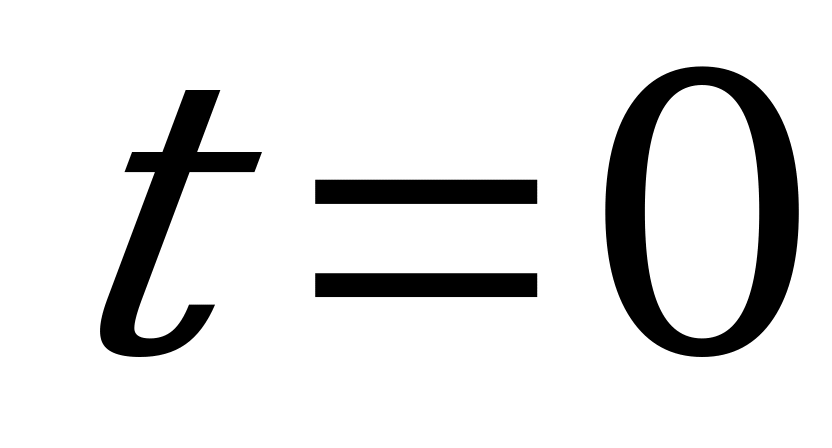 должно совпадать с началом периода. Аналогично определяются средние значения напряжения и э.д.с.
должно совпадать с началом периода. Аналогично определяются средние значения напряжения и э.д.с.
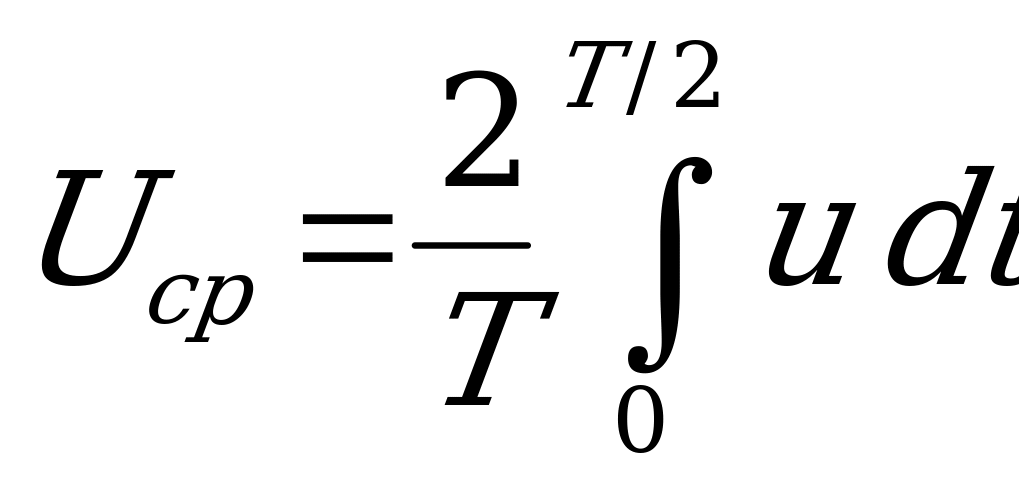 и
и 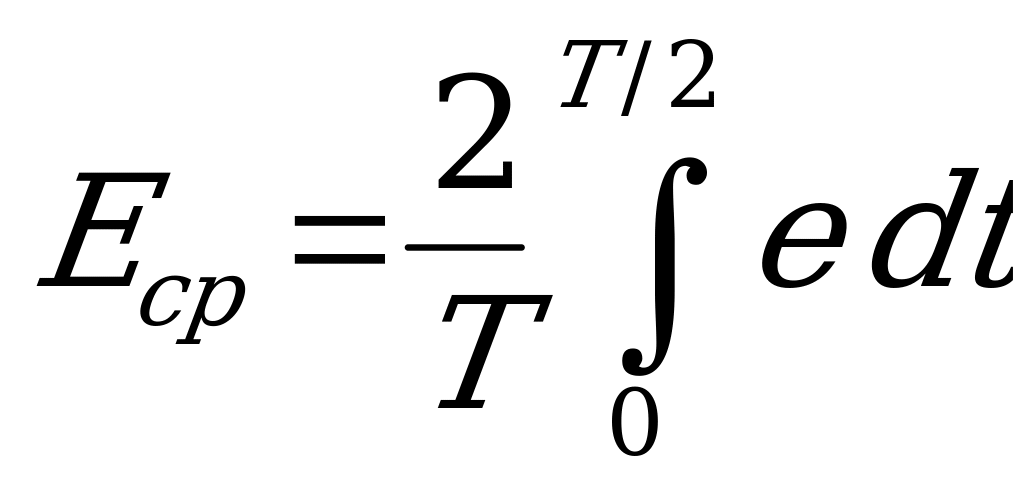 .
.
Среднее за полупериод значение тока можно представить графически высотой прямоугольника с основанием, равным  , и площадью, равной площади, которая ограничена осью абсцисс и кривой тока от начала периода до половины периода.
, и площадью, равной площади, которая ограничена осью абсцисс и кривой тока от начала периода до половины периода.
 i
i



IM Icp=0,63IM t

 0
0

T/2
Среднее значение тока за полупериод
Среднее значение синусоидального тока можно выразить через его амплитудное значение следующим образом:
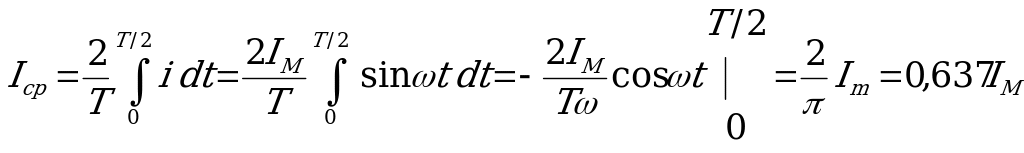 .
.
Такое же соотношение имеет место для напряжения т для э.д.с.
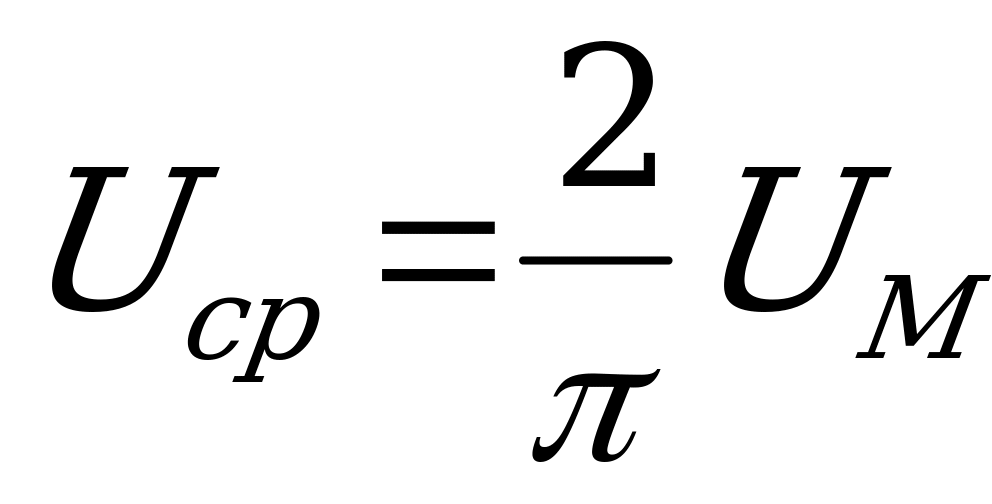 и
и 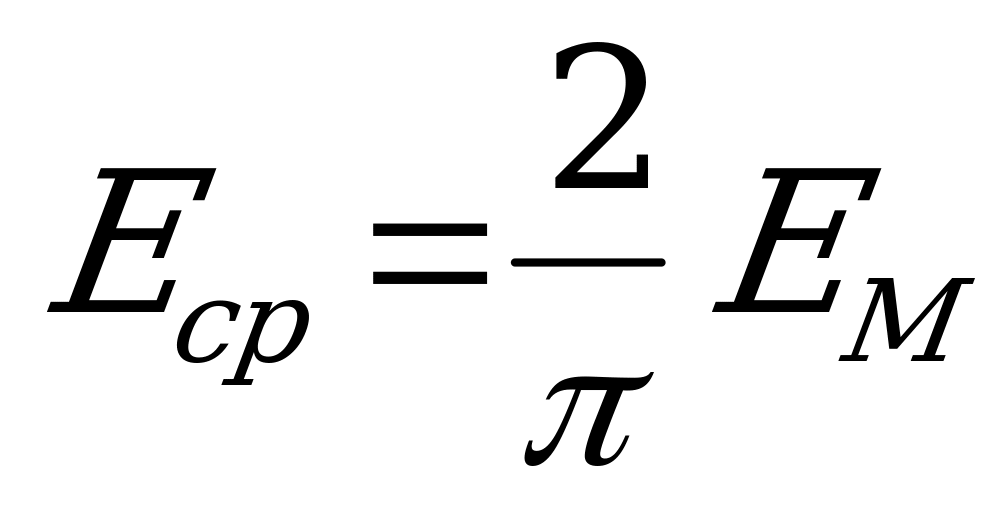 .
.
Синусоидальные величины изображают кривыми – синусоидами или вращающимися векторами. Последний способ позволяет значительно упростить графическое изображение синусоидальных величин и графическое определение суммы и разности нескольких величин.
Изображение синусоидальной величины вращающимся вектором.
При изображении синусоидальной величины, например э.д.с. 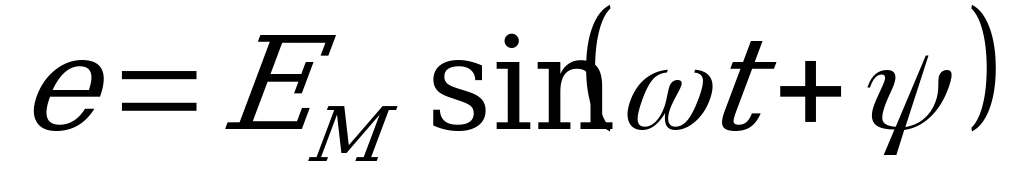 , вращающимся вектором длина его ОА в определенном масштабе представляет амплитуду
, вращающимся вектором длина его ОА в определенном масштабе представляет амплитуду 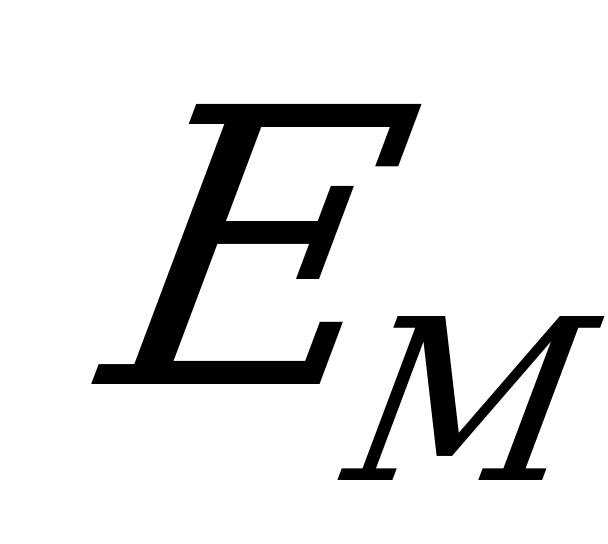 ; угол, образованный вектором с положительной полуосью абсцисс
; угол, образованный вектором с положительной полуосью абсцисс 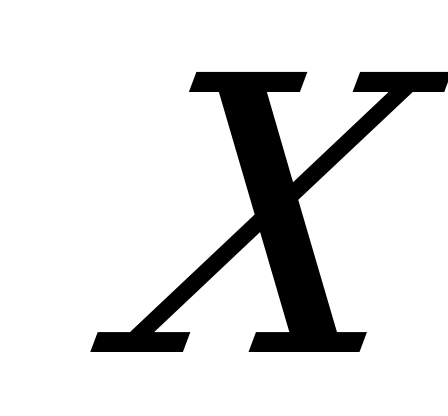 , в начальный момент времени
, в начальный момент времени 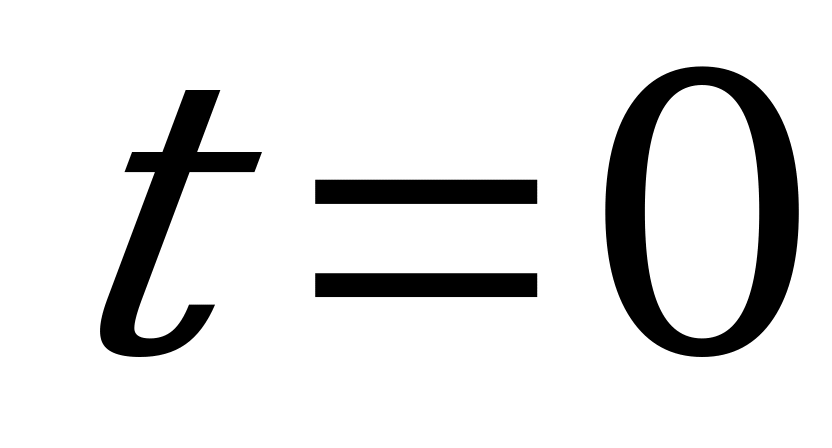 равен начальной фазе
равен начальной фазе 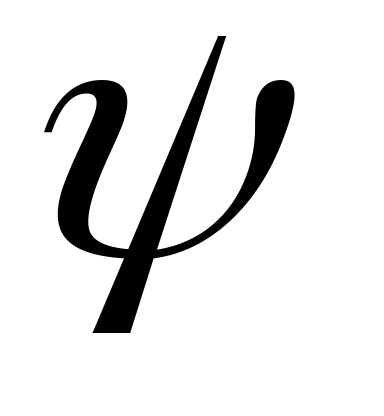 , а угловая скорость вращения вектора равна угловой частоте
, а угловая скорость вращения вектора равна угловой частоте 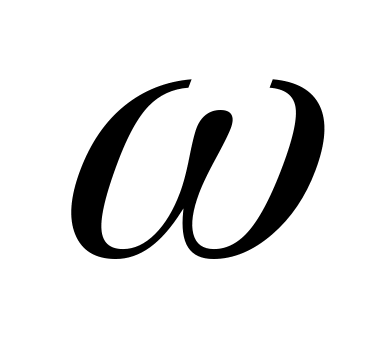 . Проекция вектора на ось ординат
. Проекция вектора на ось ординат 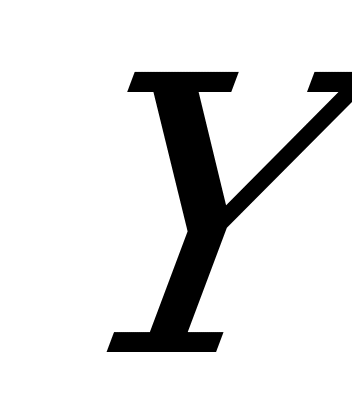 в том же масштабе дает мгновенное значение э.д.с.
в том же масштабе дает мгновенное значение э.д.с.  .
.
Действительно, в момент времени 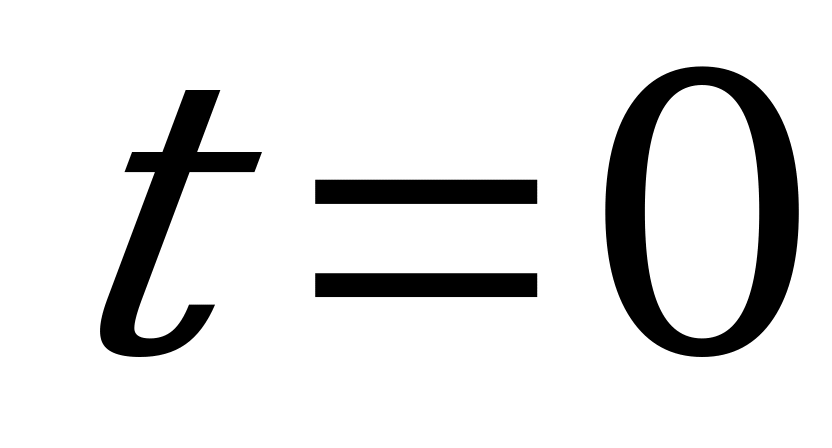 э.д.с.
э.д.с. 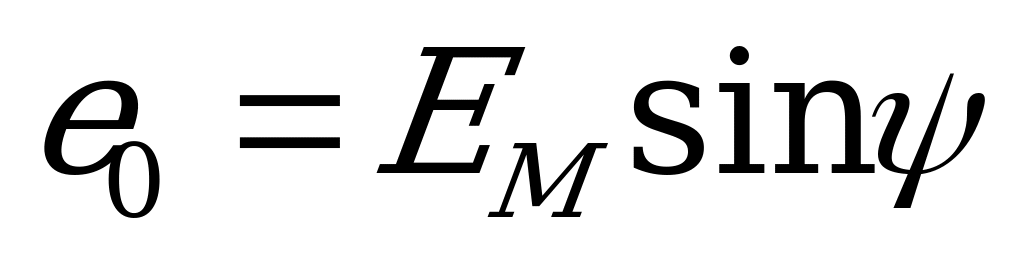 выражается проекцией вектора
выражается проекцией вектора 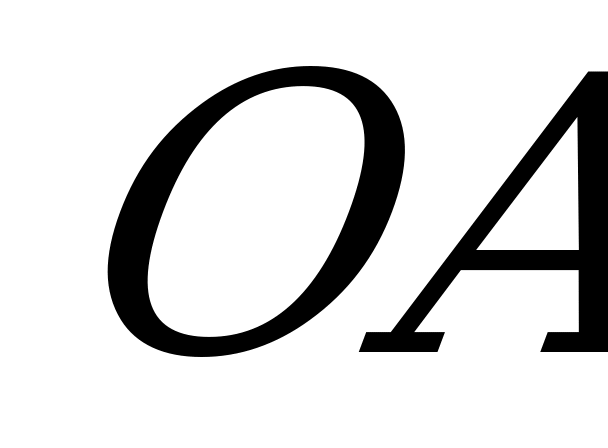 на ось
на ось 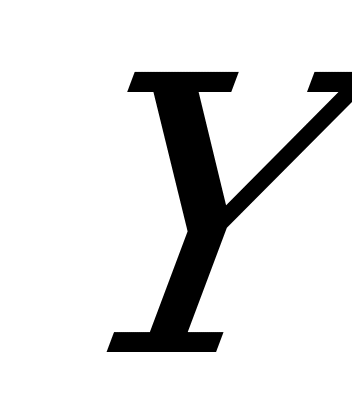 . В момент времени
. В момент времени 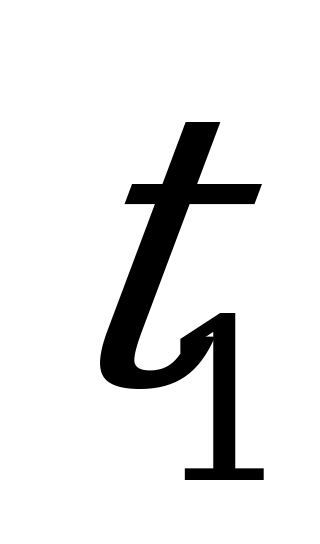 , э.д.с.
, э.д.с. 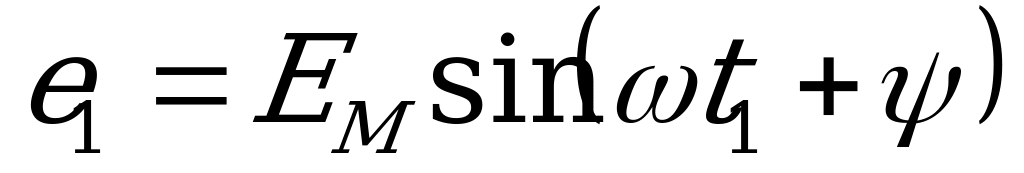 выражается проекцией вектора, занявшего новое положение
выражается проекцией вектора, занявшего новое положение 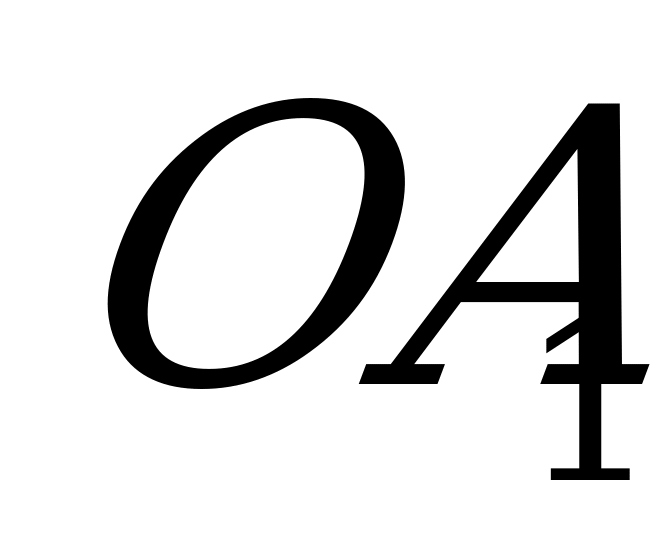 на ось
на ось 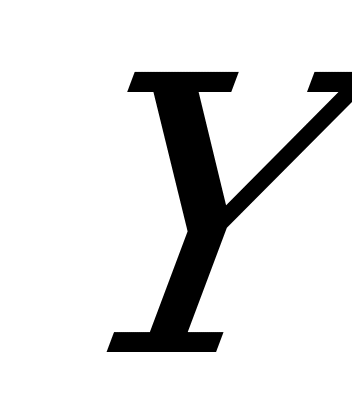 .
.
Совокупность нескольких векторов, изображающих синусоидальные величины одной частоты, называется векторной диаграммой.
Так как угловая скорость всех векторов на векторной диаграмме одинакова, то возможное расположение их на диаграмме не меняется. Начало отсчета времени для периодической кривой можно выбрать произвольно, поэтому при построении один из векторов на вертикальной диаграмме можно расположить произвольно, а остальные векторы располагать по отношению к нему под углом, равным углам сдвига фаз.
Сложение двух синусоидальных величин можно заменить сложением векторов, каждый из которых изображает соответствующую синусоидальную величину. Например, если даны две э.д.с. 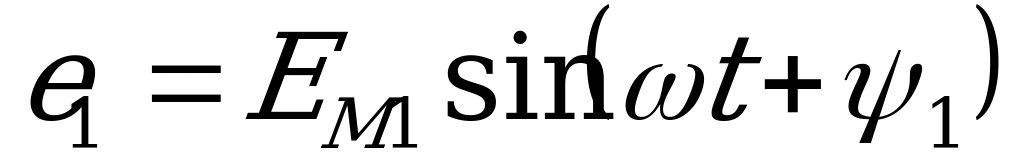 и
и 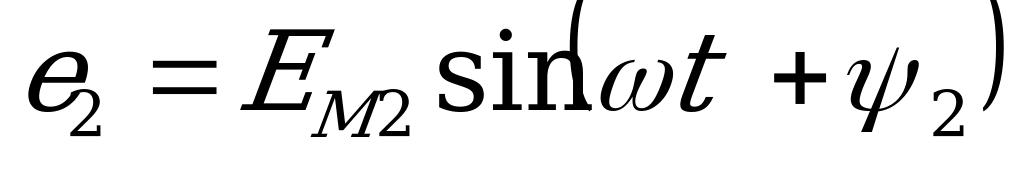 , представленные векторами ОА и ОБ , то для сложения вектор ОА переносят параллельно самому себе так, чтобы начало его совпало с концом вектора ОБ, тогда замыкающий вектор ОВ будет представлять вектор суммарной э.д.с. е. Правильность сказанного следует из того, что проекции вектора ОА и ОБ на ось ординат представляют собой мгновенные значения е1 и е2, а сумма этих проекций равна проекции вектора ОВ, представляющего собой вектор суммарной э.д.с. е.
, представленные векторами ОА и ОБ , то для сложения вектор ОА переносят параллельно самому себе так, чтобы начало его совпало с концом вектора ОБ, тогда замыкающий вектор ОВ будет представлять вектор суммарной э.д.с. е. Правильность сказанного следует из того, что проекции вектора ОА и ОБ на ось ординат представляют собой мгновенные значения е1 и е2, а сумма этих проекций равна проекции вектора ОВ, представляющего собой вектор суммарной э.д.с. е.
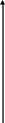 Y B
Y B


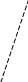


EM
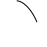


 EM2
EM2 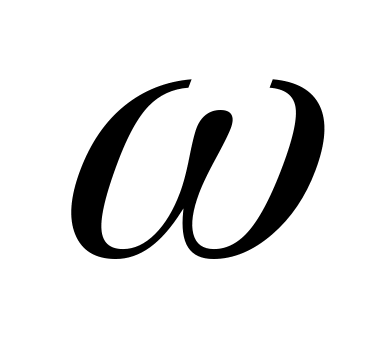
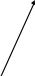
 e2 Б
e2 Б

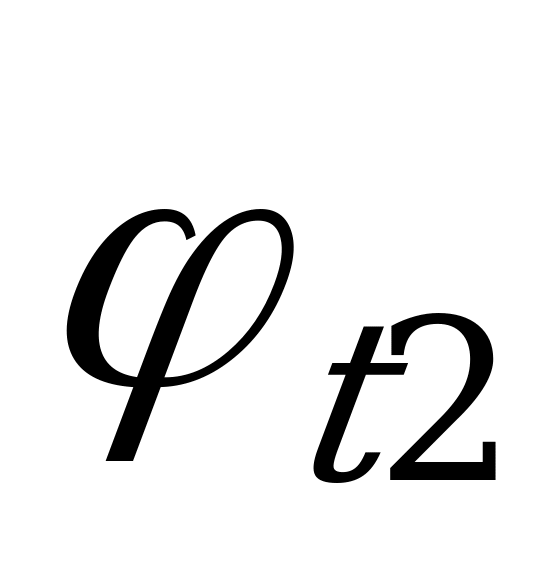

e1 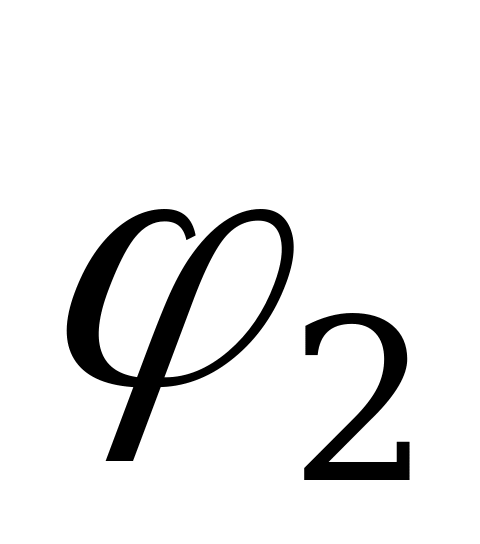 A
A



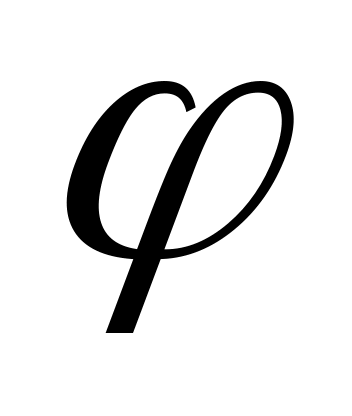 EM1
EM1
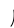 Г Х
Г Х
 0
0 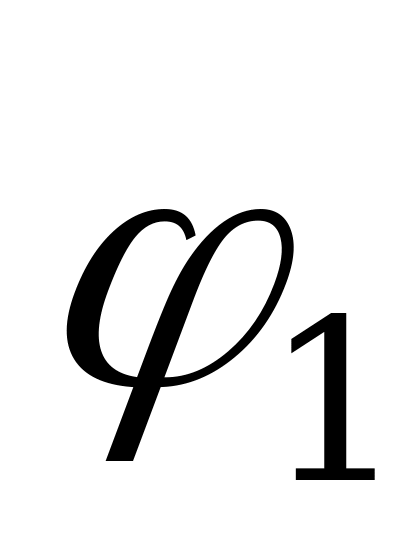
Сложение двух векторов э.д.с.
Из треугольника векторов можно найти амплитуду суммарной э.д.с. и тангенс ее начального фазного угла.
Вычитание синусоидальных величин производится как сложение уменьшаемой величины с обратной по знаку вычитаемой величины, т.е.
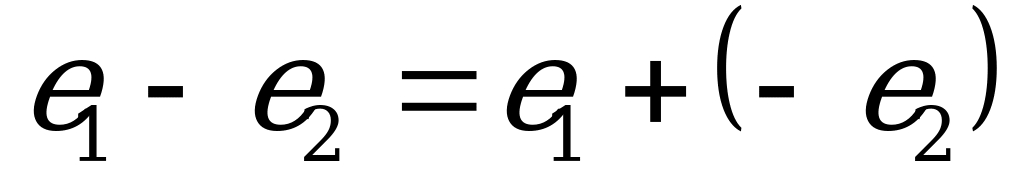 .
.
В теме «Процессы нагрева и охлаждения электрических машин» рассматривается дифференциальное уравнение теплового баланса.
 ,
,
где С - теплоемкость двигателя в целом;
 - превышение температуры двигателя над температурой внешней среды;
- превышение температуры двигателя над температурой внешней среды;
А - теплоотдача двигателя в целом;
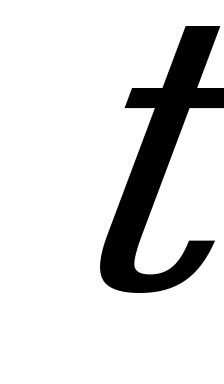 - время;
- время;
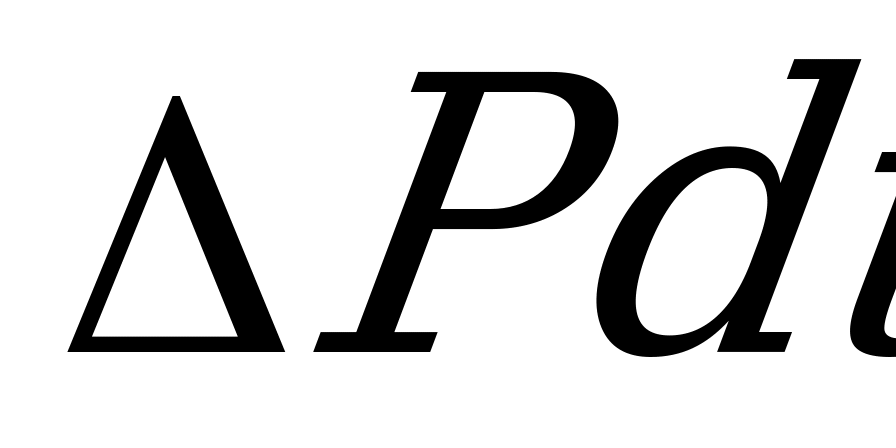 - выделенное двигателем количество тепла за время
- выделенное двигателем количество тепла за время 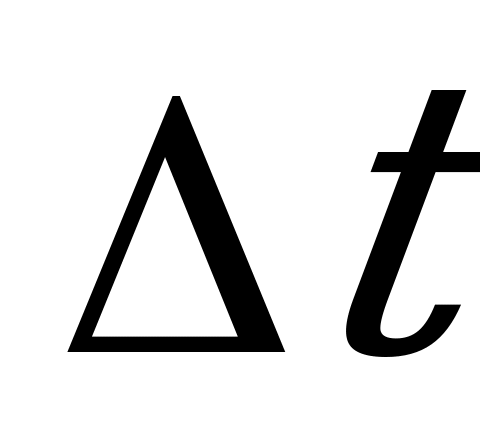 ;
;
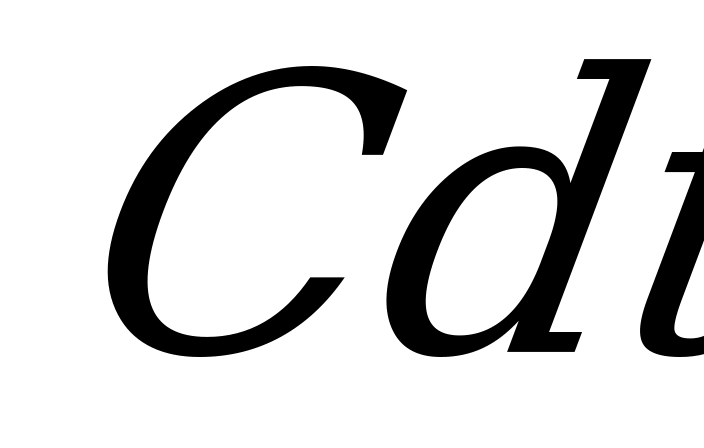 - количества тепла, увеличивающее температуру нагрева машин;
- количества тепла, увеличивающее температуру нагрева машин;
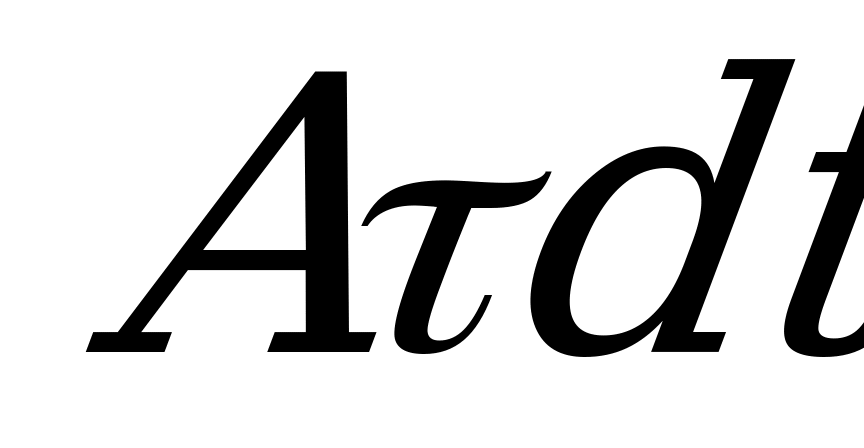 - количество тепла, рассеивающееся в окружающей среде.
- количество тепла, рассеивающееся в окружающей среде.
Допуская, что нагрузка, а следовательно и потери 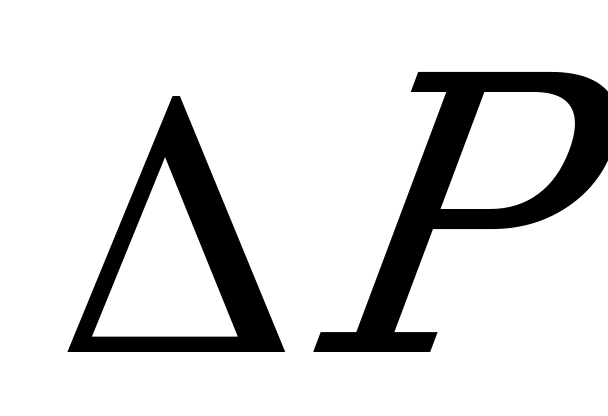 постоянны в пределах рассматриваемого промежутка времени
постоянны в пределах рассматриваемого промежутка времени  , получим
, получим
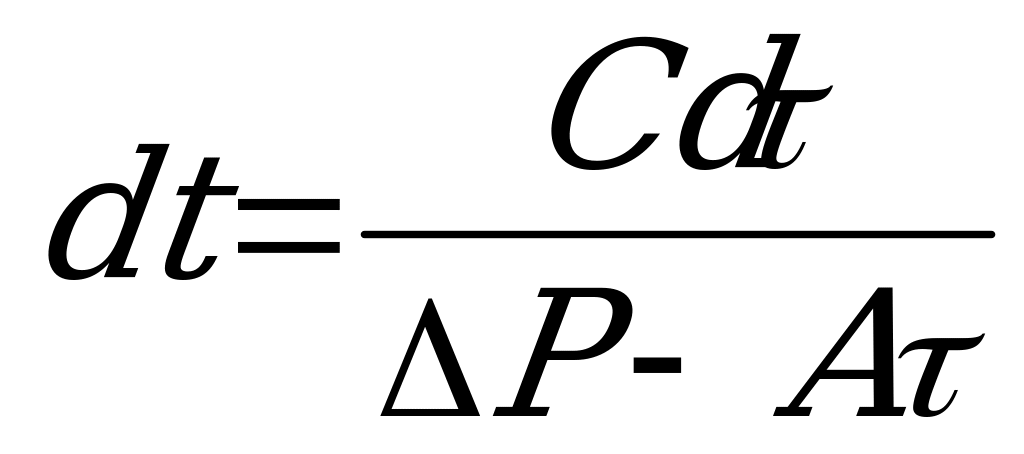 .
.
Предмет «Открытая разработка месторождений полезных ископаемых» применяет формулы тригонометрии в теме «Порядок и методы определения конечных контуров карьера».
Объем массы, заключенный в торцевом борту карьера находят по формуле:
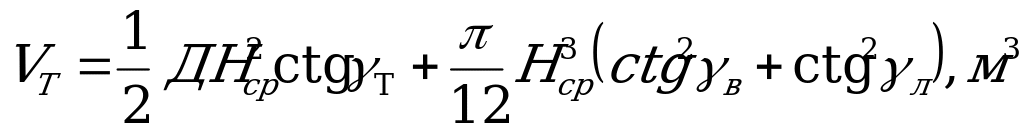 , где
, где
Д – ширина дна карьера;
Нср - средняя глубина торцевого борта;
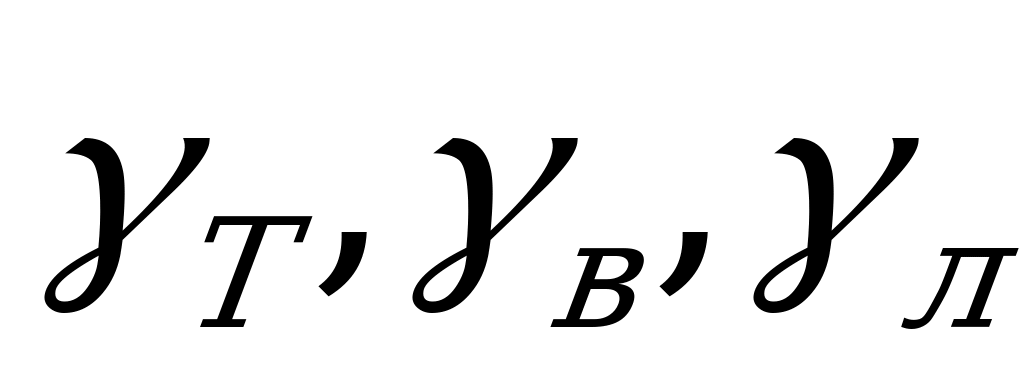 - углы откосов соответственно торцового борта и бортов по висячему и лежачему боку.
- углы откосов соответственно торцового борта и бортов по висячему и лежачему боку.
В других предметах применение более широкое. Например, при изучении предметов «Техническая механика», «Сопротивление материалов» рассматриваются физические, технологические и механические свойства материалов. В этом предмете дифференциальное и интегральное исчисления являются основой для большинства вычислений.
Алгебраические суммы произведений площадей частей плоской фигуры на расстояние их центров тяжести до соответствующей оси называют статическими моментами площадей относительно осей. Следовательно, 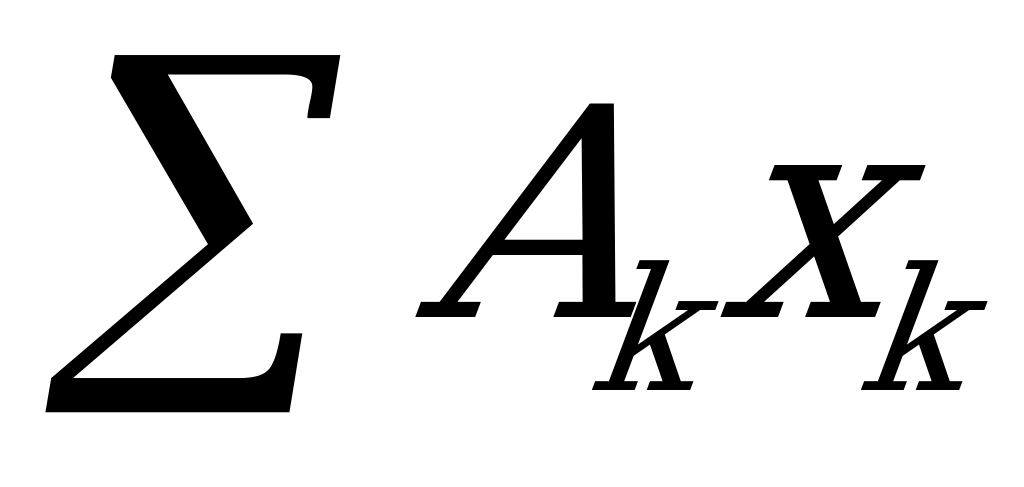 - статический момент площади относительно оси у;
- статический момент площади относительно оси у; 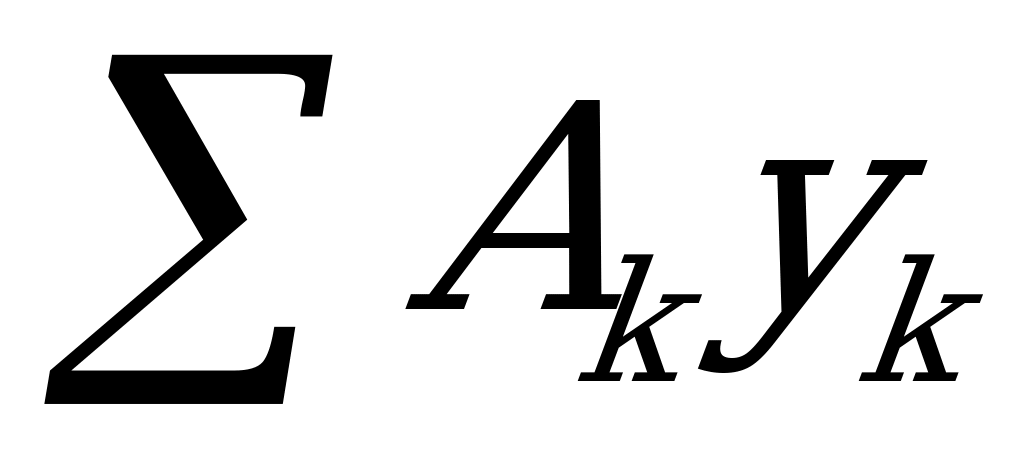 - статический момент площади относительно оси х.
- статический момент площади относительно оси х.
Обозначив статические моменты соответственно 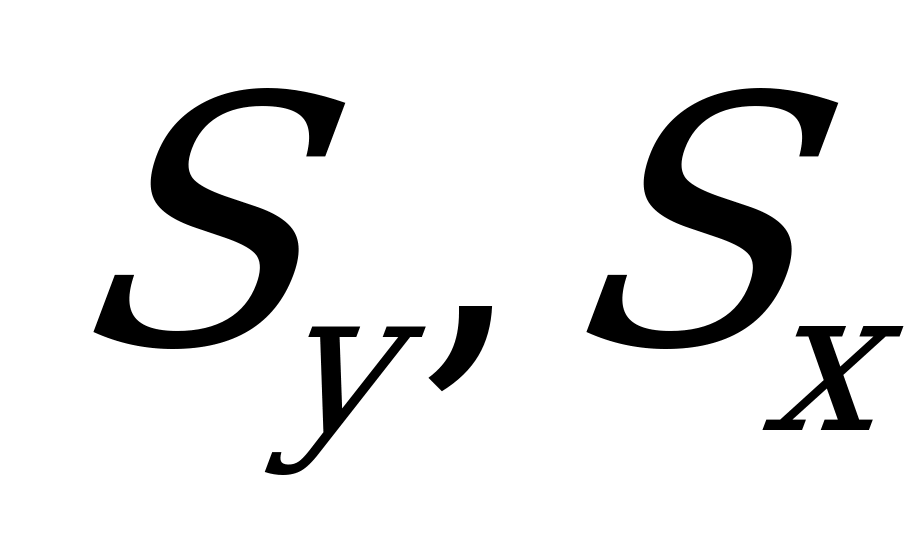 и приняв во внимание, что
и приняв во внимание, что 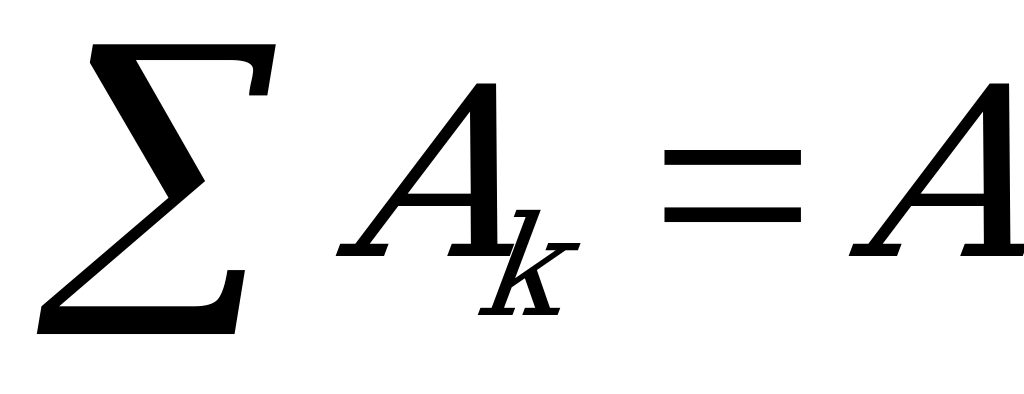 - площади всей плоской фигуры, последние две формулы примут вид
- площади всей плоской фигуры, последние две формулы примут вид
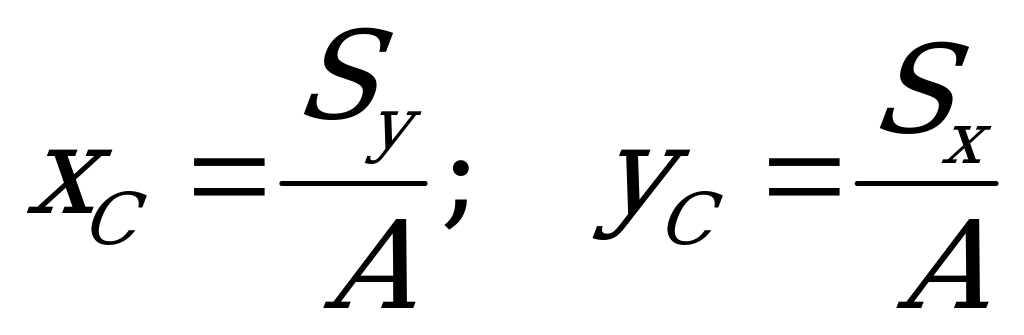 . (1.65)
. (1.65)
Отсюда 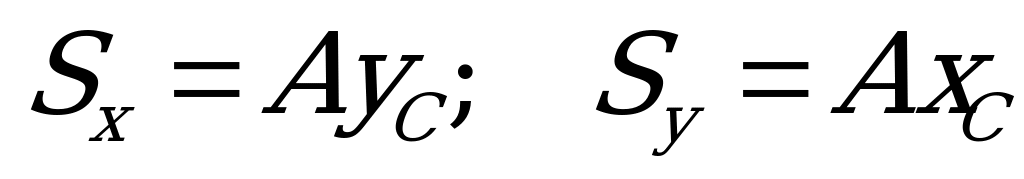 , (1. 66)
, (1. 66)
т.е. статический момент площади относительно оси абсцисс равен произведению площади фигуры на ординату ее центра тяжести, а статический момент относительно оси ординат – произведению площади фигуры на абсциссу ее центра тяжести.
Статический момент плоской фигуры выражается в м3, см3 или в мм3.
а) б)

 у
у
y




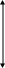





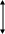

 С h x
С h x
C
yC



 x
x

xC
b

Пример. Определить статические моменты площади прямоугольника со сторонами b=20см и h=14см относительно осей х и у (рис. а).
Решение. 1. Площадь прямоугольника 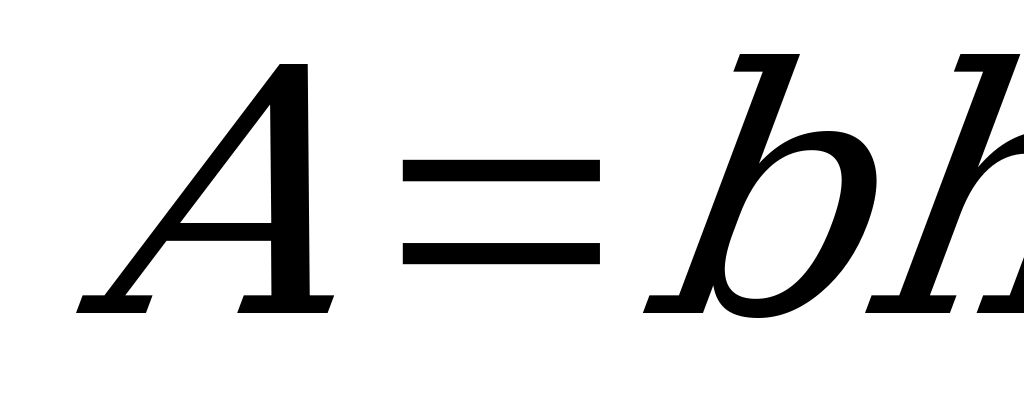 , а координаты центра тяжести С
, а координаты центра тяжести С 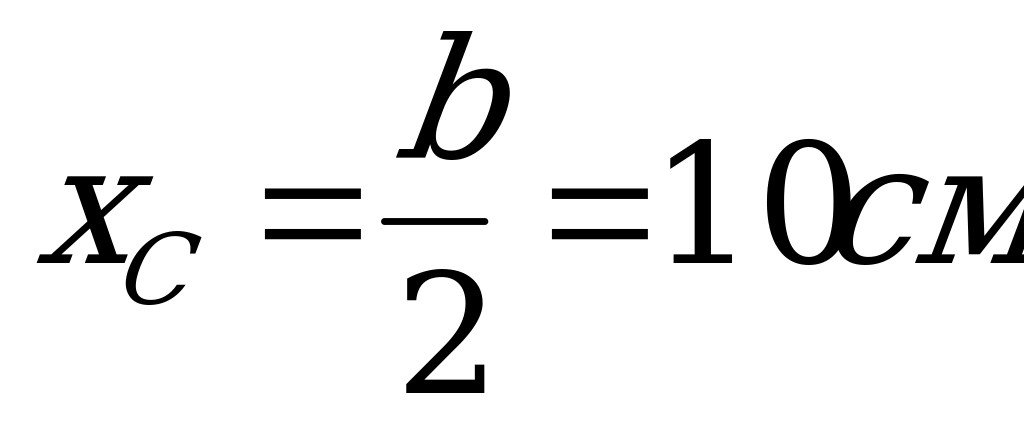 и
и 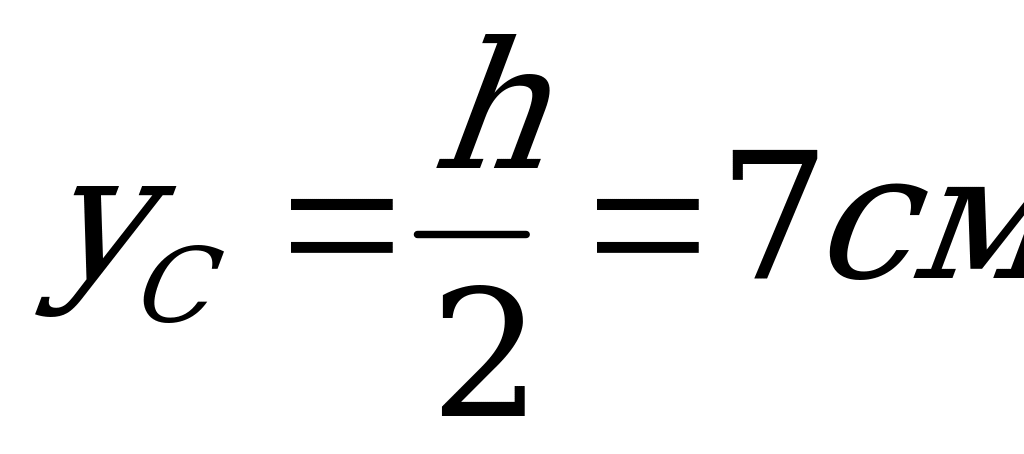 .
.
По формулам (1. 66) находим:
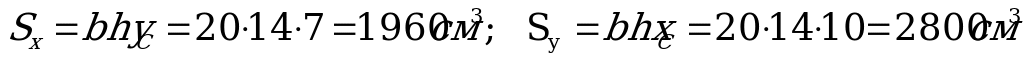 .
.
Из равенства (1.66) следует важное свойство статического момента: статический момент плоской фигуры относительно центральной оси (оси, проходящей через центр тяжести плоской фигуры) равен нулю.
Действительно, если в выше предоставленном примере начало осей координат поместить в точке С (рис. б), то при любом положении осей х и у каждая из них будет центральной и в этом случае 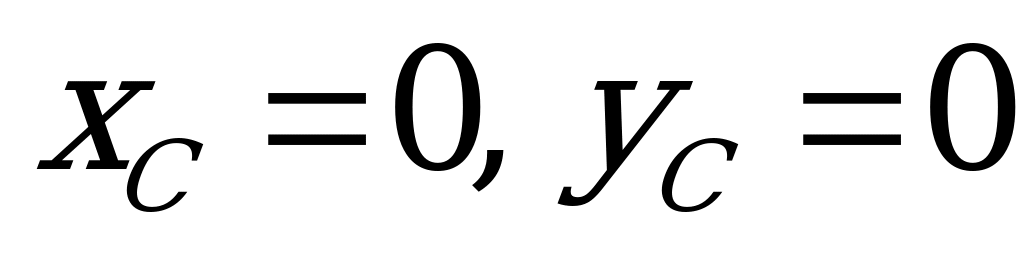 . Значит,
. Значит, 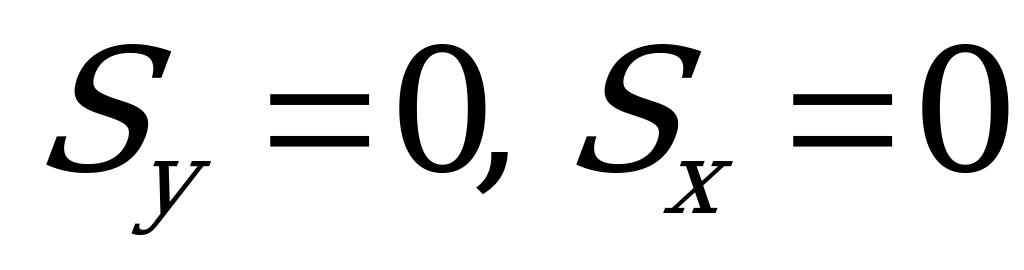 .
.
В случае произвольной плоской фигуры

 y x
y x




 dA
dA


 xC
xC




y
yC
 0 x
0 x
ее площадь находят интегрированием:
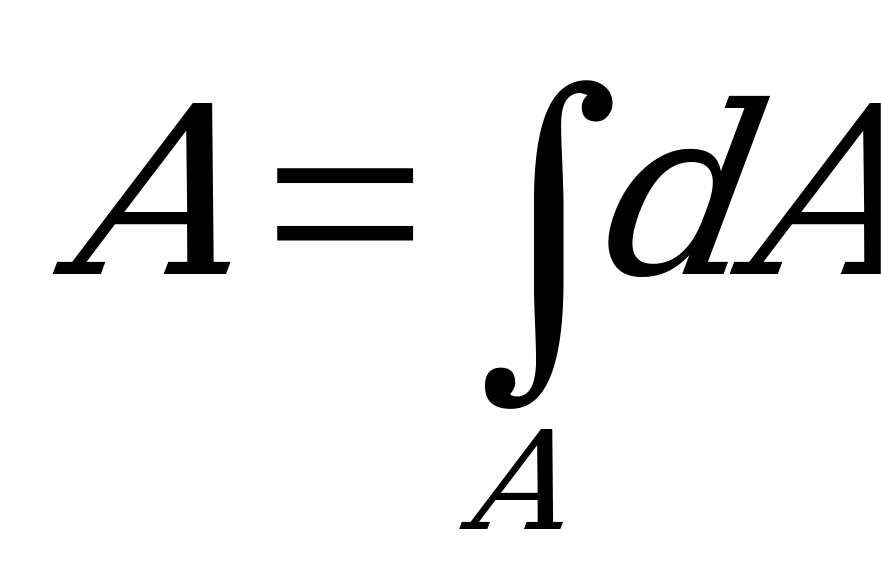 . (1.67)
. (1.67)
Интегрированием определяют и статические моменты таких плоских фигур:
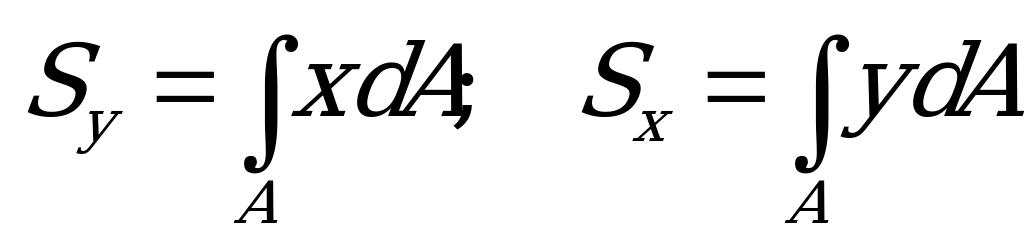 . (1.68)
. (1.68)
Здесь  - элементарные площадки плоской фигуры (дифференциал площади); х и у – расстояния от элементарных площадок до осей, знак А у интегралов означает, что интегрирование производится по всей площади.
- элементарные площадки плоской фигуры (дифференциал площади); х и у – расстояния от элементарных площадок до осей, знак А у интегралов означает, что интегрирование производится по всей площади.
Исходя из выражений (1.67) и (1.68), формулы координат центра тяжести произвольной плоской фигуры в интегральной форме примут вид
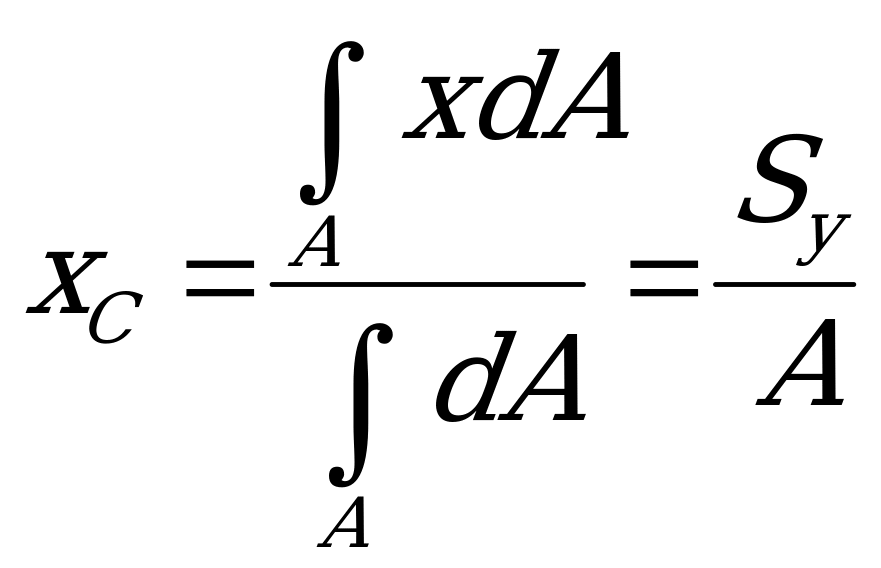 ;
; 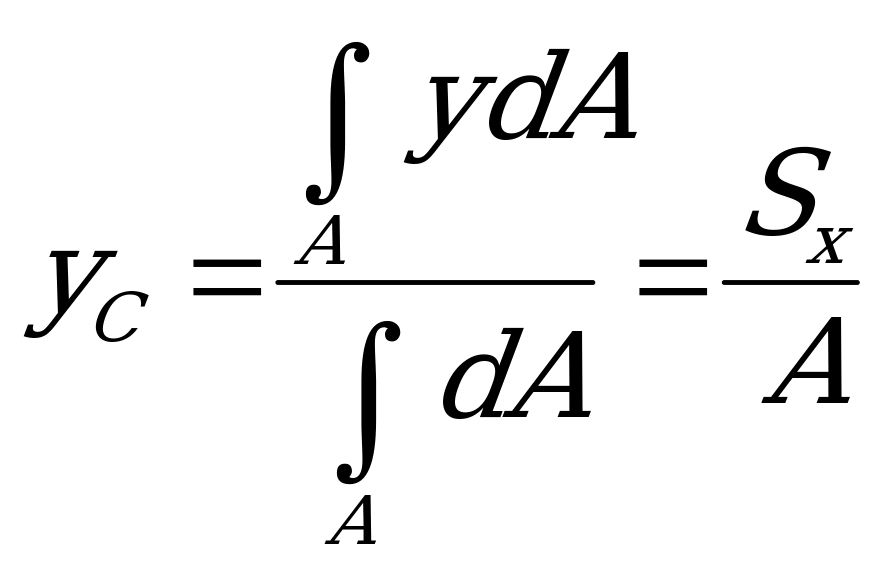 (1.69)
(1.69)
полностью соответствуют формулам (1.65).
Центр тяжести параболического треугольника.
Параболическим треугольником называется фигура, ограниченная дугой параболы 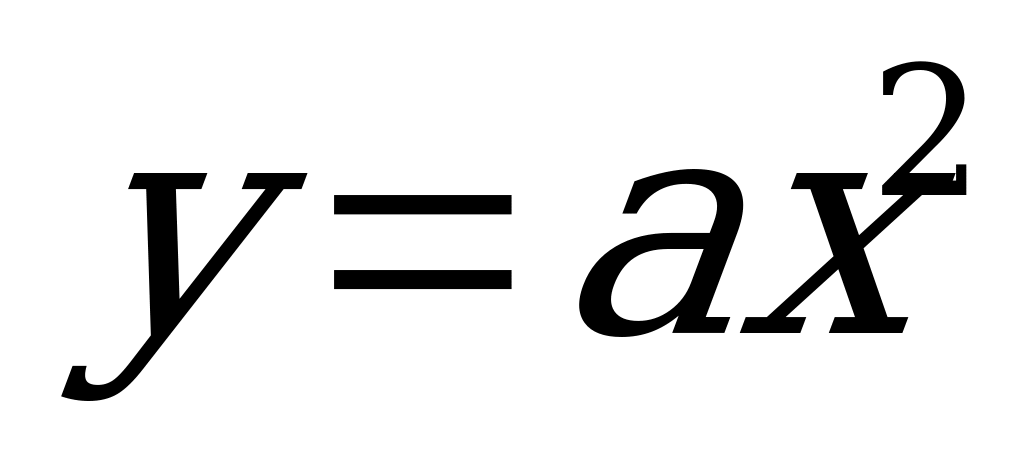 с вершиной в начале координат, осью абсцисс и ординатой
с вершиной в начале координат, осью абсцисс и ординатой 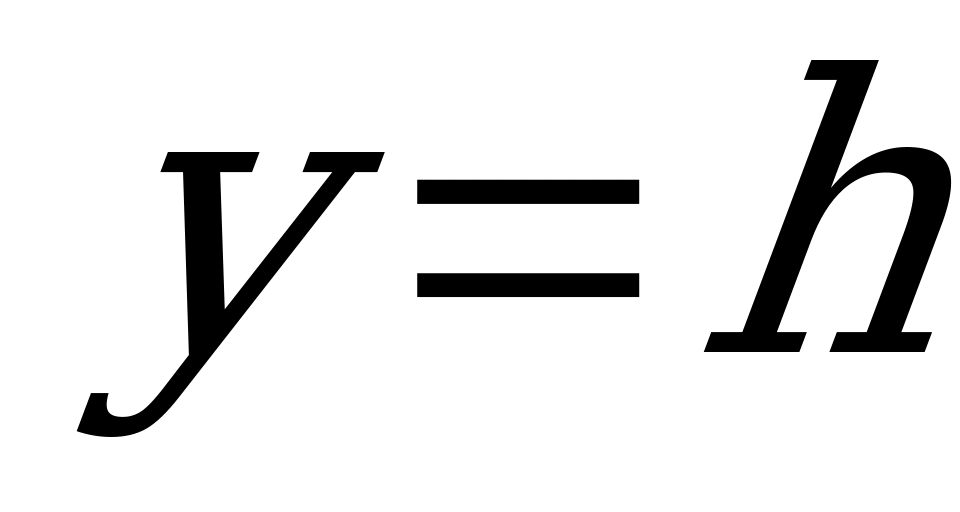 . Для определения координат центра тяжести параболического треугольника используем формулы (1.67), (1.68), (1.69).
. Для определения координат центра тяжести параболического треугольника используем формулы (1.67), (1.68), (1.69).
 y
y
 y=ax2
y=ax2

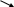



 dy dA’
dy dA’









 h=ab2
h=ab2


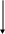




 x dx (b-x)
x dx (b-x)



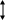 y
y 
 da y=3h/10
da y=3h/10

xC=3b/4 b/4


b

Разобьем площадь треугольника на полоски бесконечно малой ширины 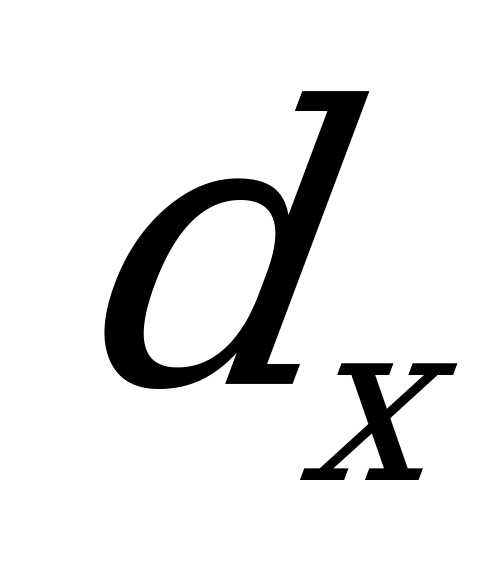 и переменной высоты
и переменной высоты 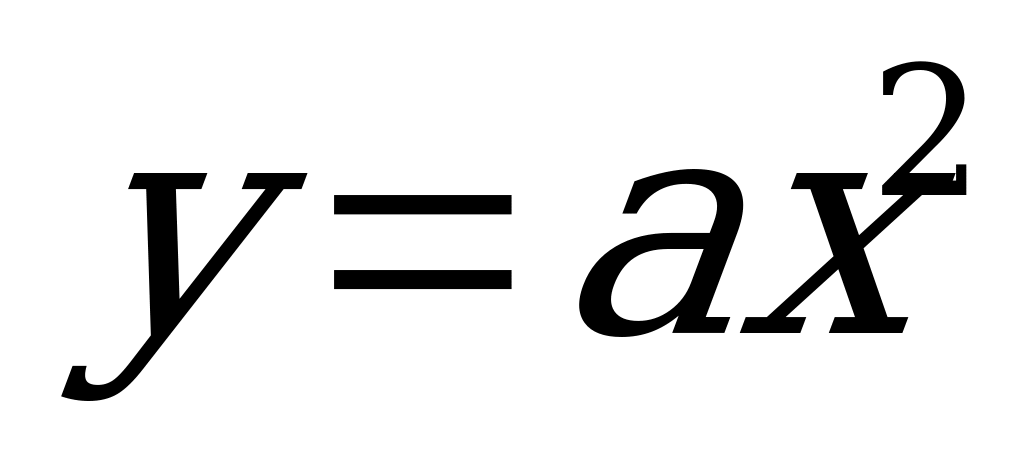 . Тогда элементарная площадка
. Тогда элементарная площадка 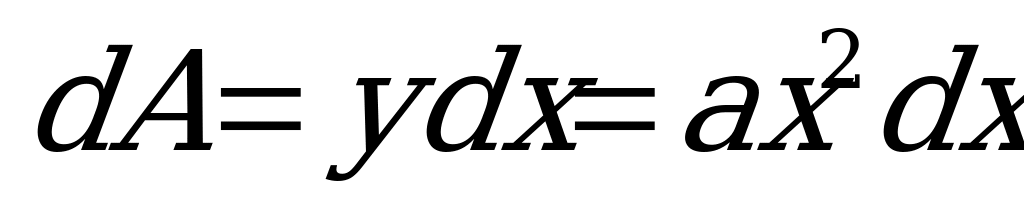 . Подставив значение
. Подставив значение  в выражение
в выражение 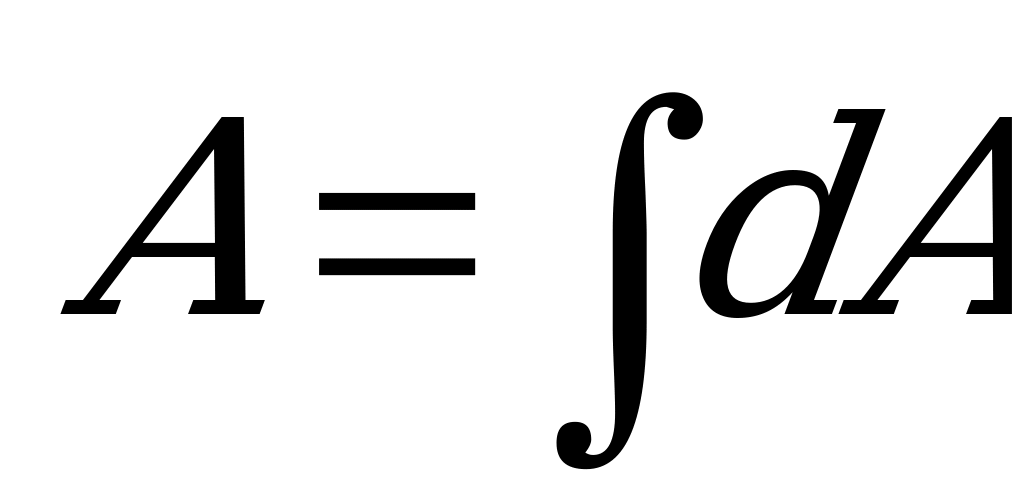 и проинтегрировав по всей площади, т.е. при изменении
и проинтегрировав по всей площади, т.е. при изменении 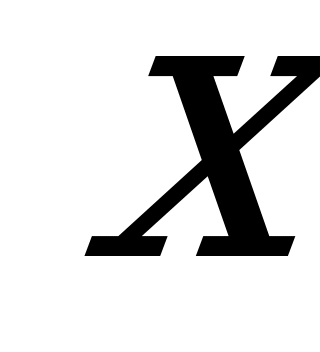 от
от 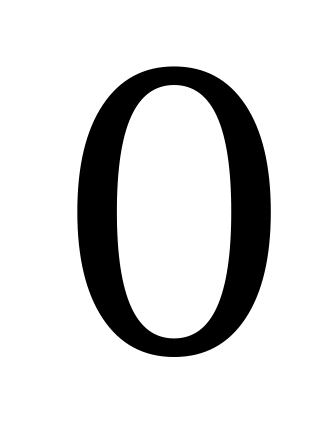 до
до 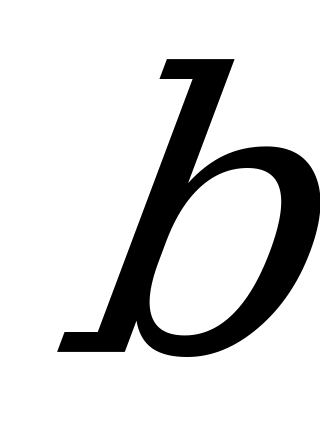 , получим
, получим
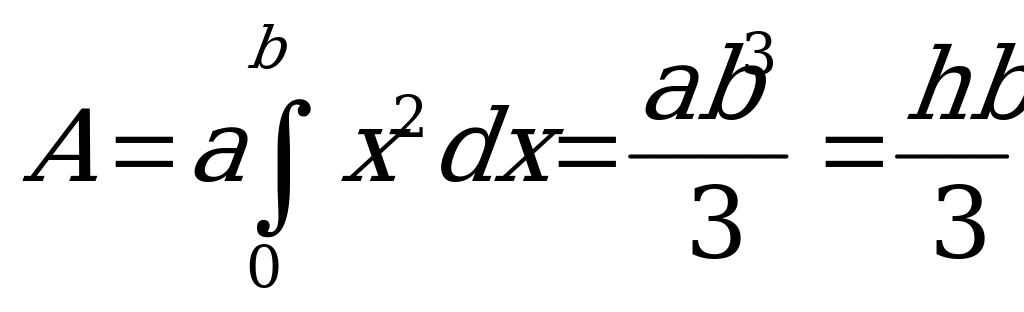 .
.
Статический момент элементарной площадки  относительно оси
относительно оси 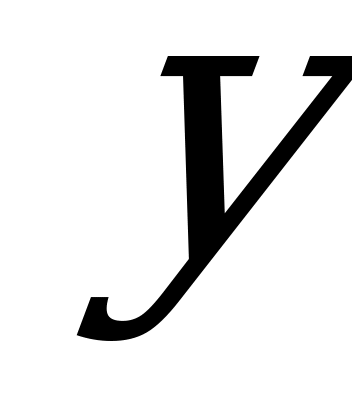
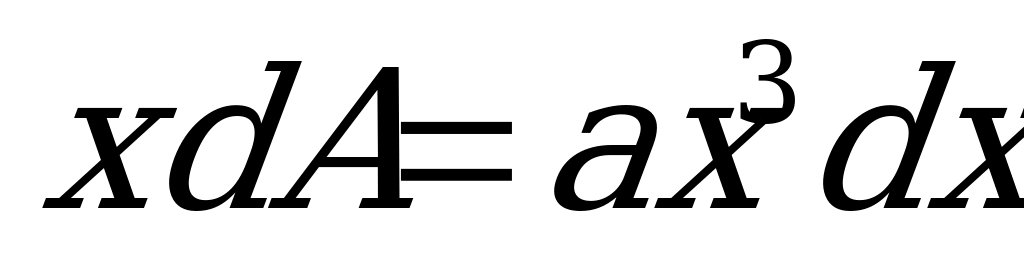 . Проинтегрировав это выражение по всей площади параболического треугольника (т.е. в пределах изменения
. Проинтегрировав это выражение по всей площади параболического треугольника (т.е. в пределах изменения 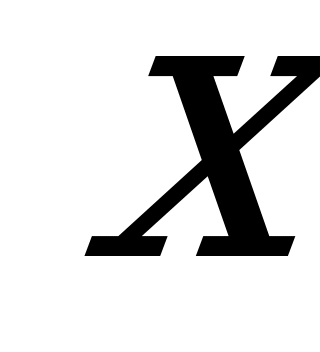 от
от 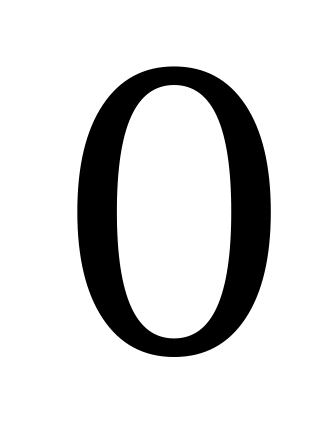 до
до 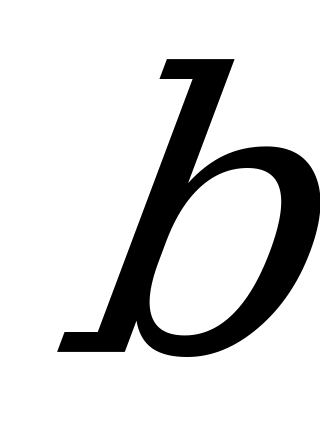 ), получим
), получим
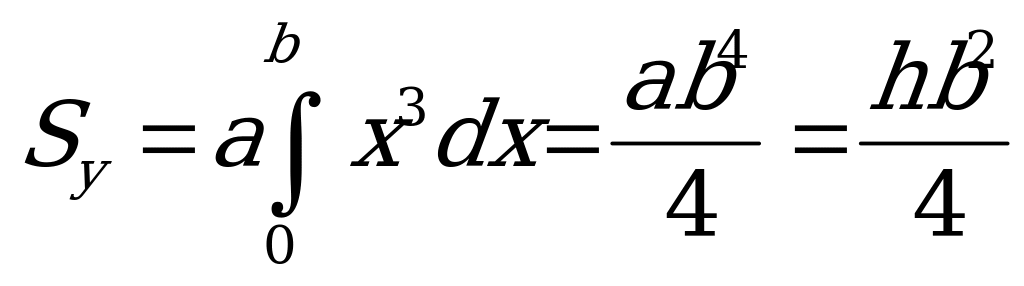 .
.
Для определения статического момента параболического треугольника относительно оси х разобьем его на полоски бесконечно малой высоты 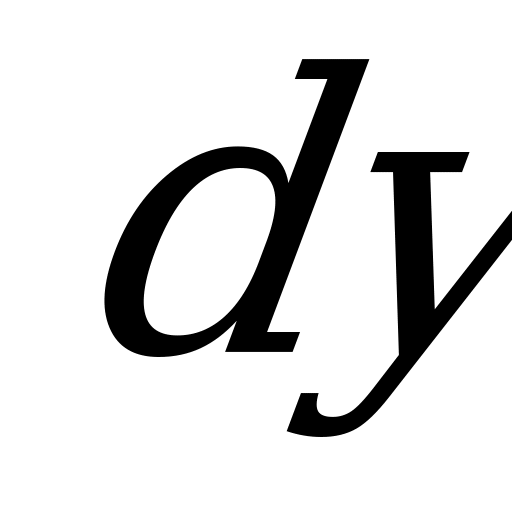 и ширины
и ширины 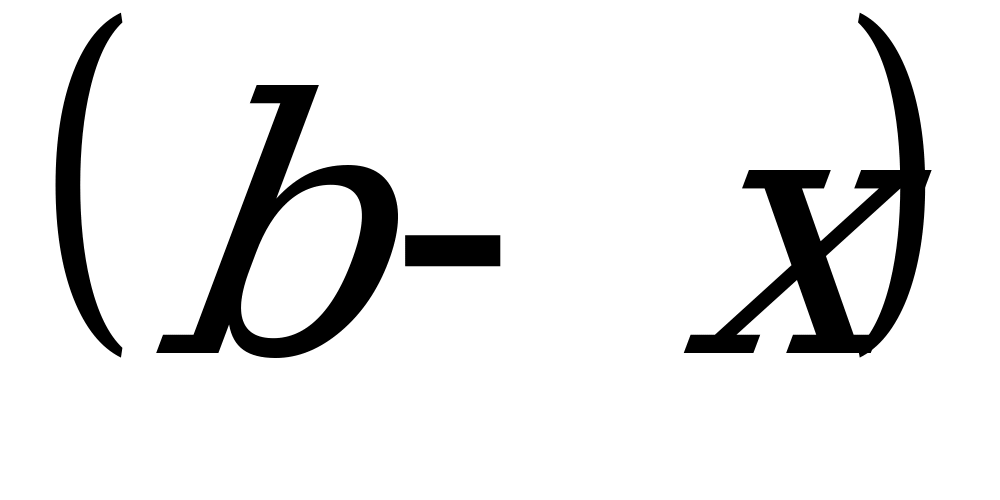 , тогда элементарная площадка
, тогда элементарная площадка
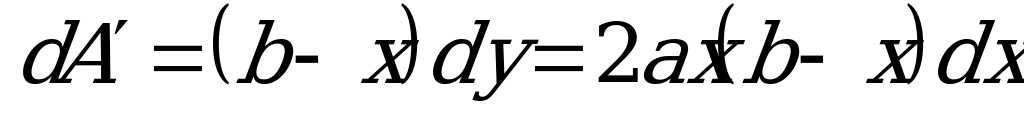 ,
,
так как 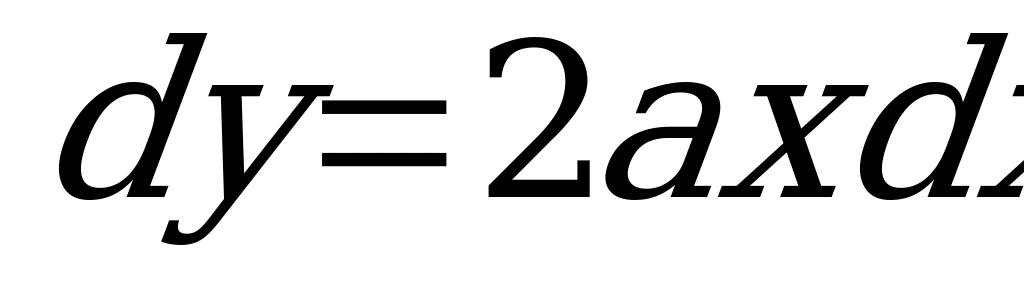 . Следовательно, статический момент элементарной площадки относительно оси
. Следовательно, статический момент элементарной площадки относительно оси 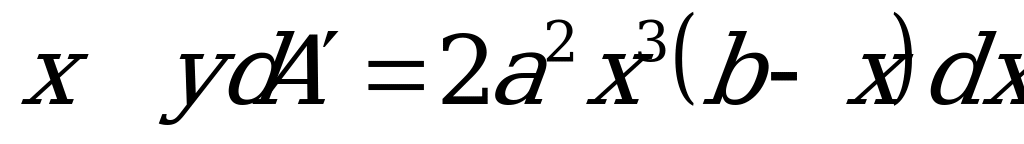 .
.
Проинтегрировав это выражение по всей площади, получим
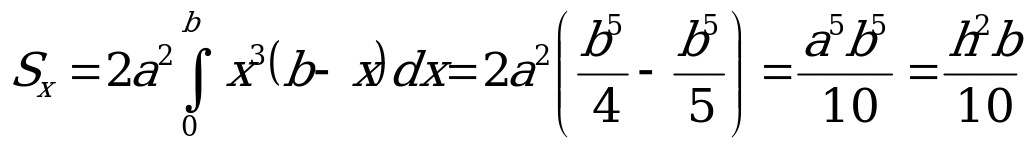 .
.
Из формул 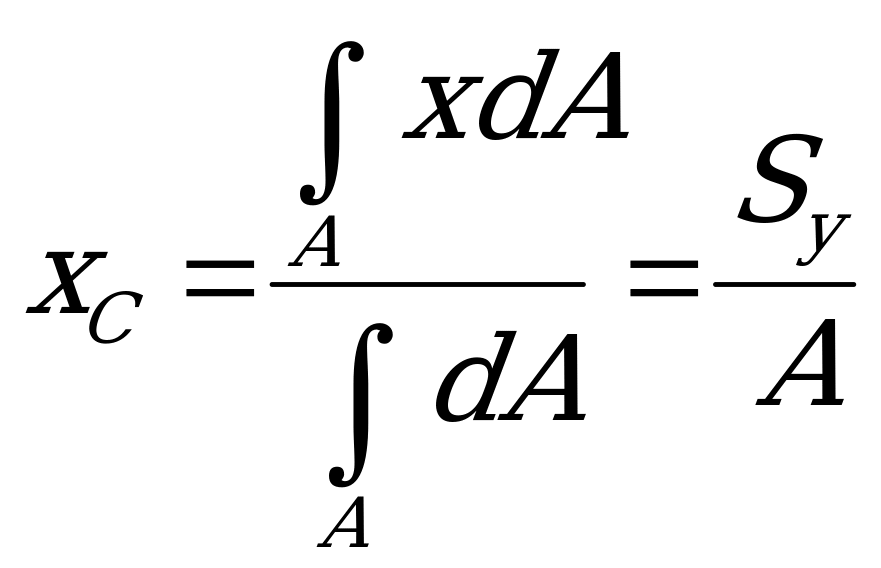 ;
; 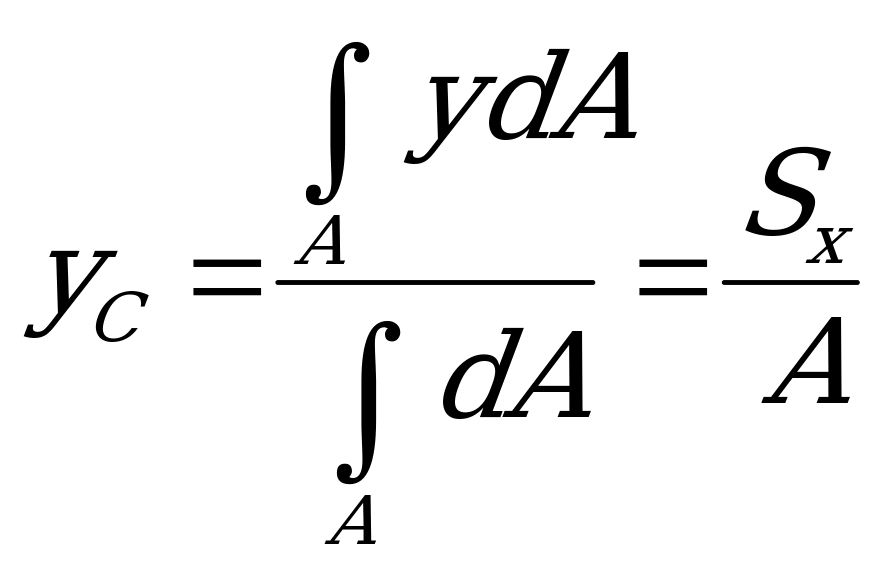 получаем координаты центра тяжести:
получаем координаты центра тяжести:
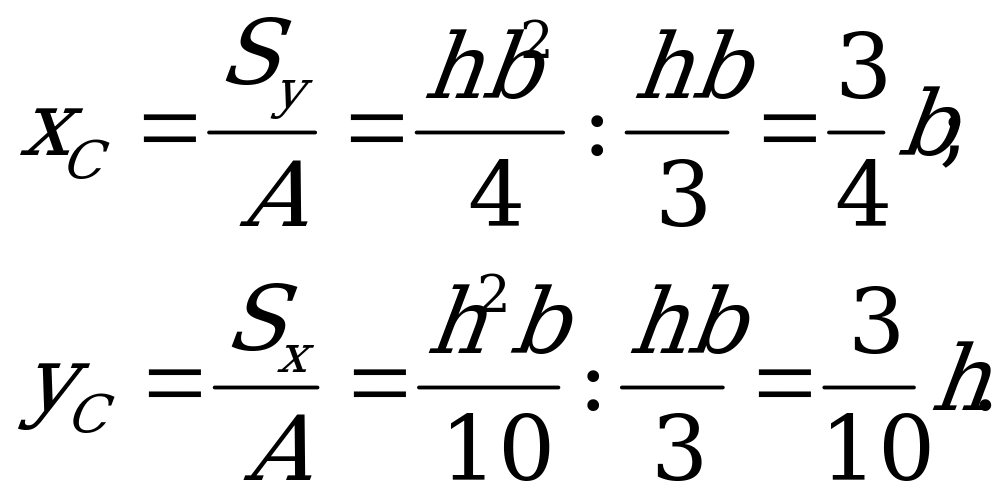
Моменты инерции некоторых тел
Воспользовавшись общей формулой 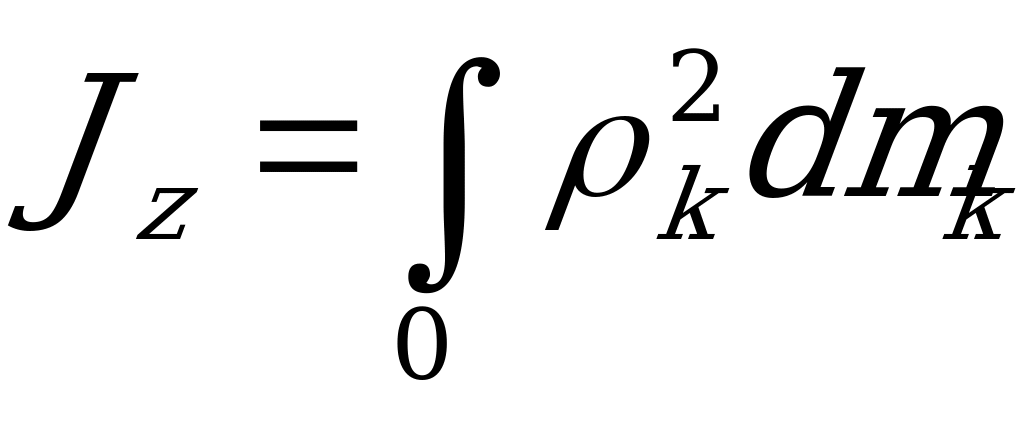 , выведем формулы моментов инерции некоторых тел.
, выведем формулы моментов инерции некоторых тел.
Моменты инерции тонкого однородного стержня массой 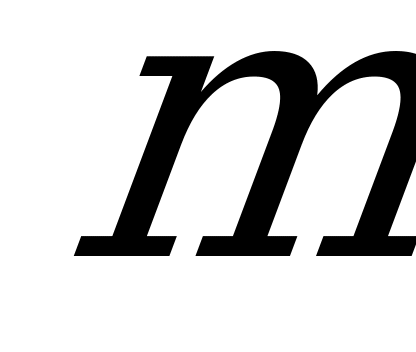 и длиной
и длиной 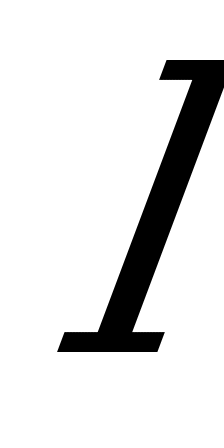 относительно оси, перпендикулярной стержню и расположенной у одного из его концов (1.176).
относительно оси, перпендикулярной стержню и расположенной у одного из его концов (1.176).


 z y dy dm
z y dy dm






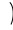





 0 l
0 l
1.176
Выделим на расстоянии 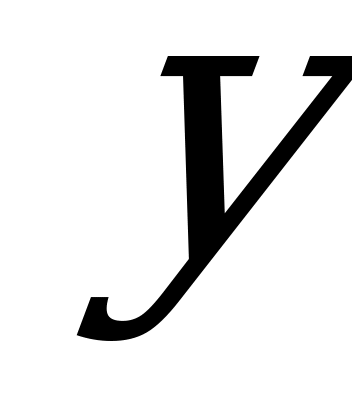 от оси
от оси  элемент стержня
элемент стержня 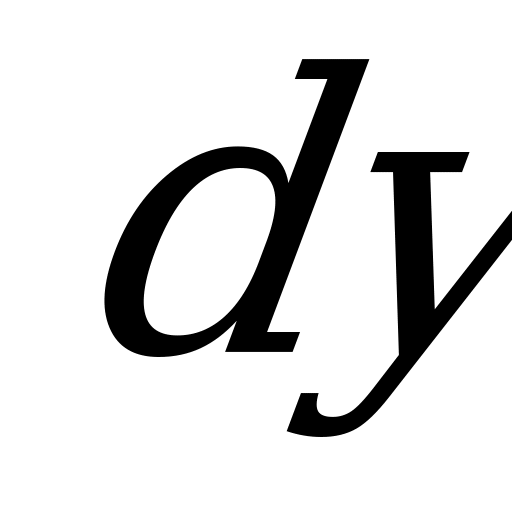 и массой
и массой 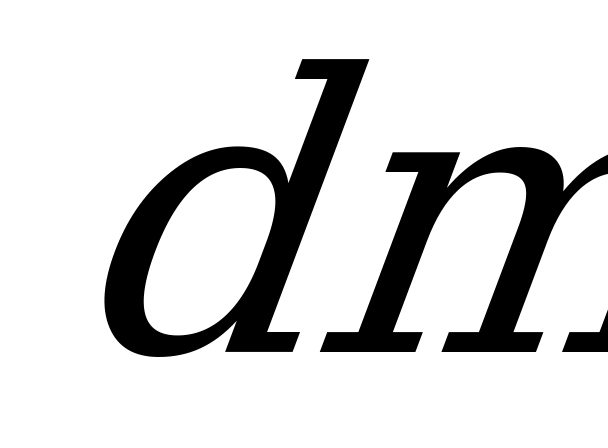 . Принимая во внимание однородность стержня и постоянство поперечного сечения по всей длине, можно считать, что
. Принимая во внимание однородность стержня и постоянство поперечного сечения по всей длине, можно считать, что 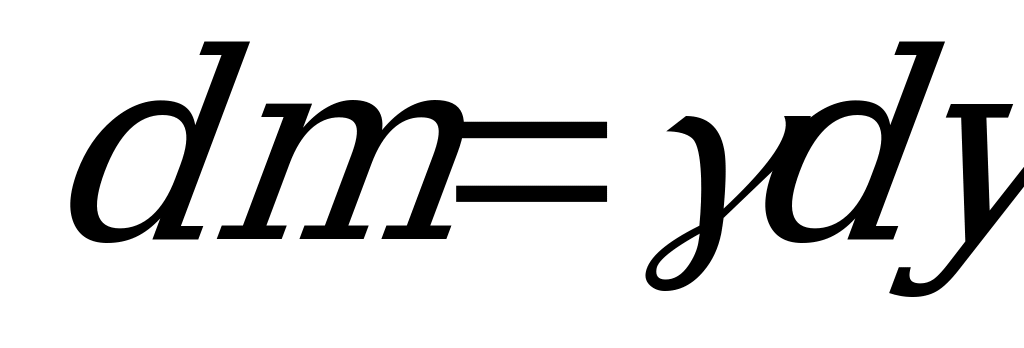 , где
, где 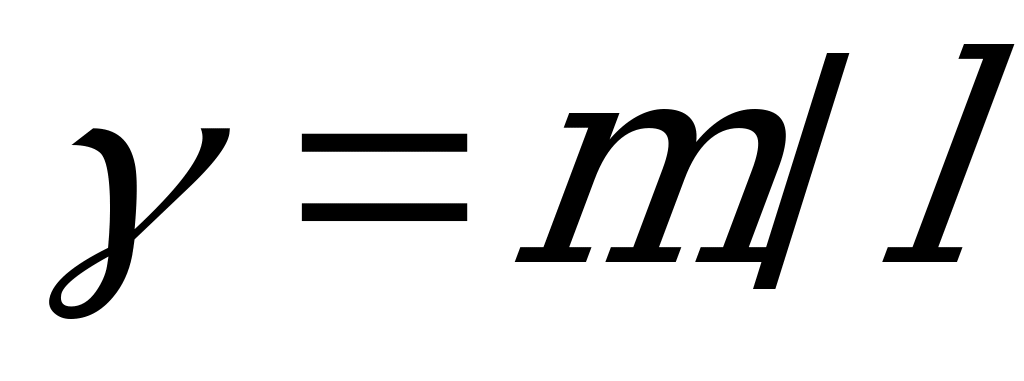 - масса длины стержня. Тогда элементарный момент инерции
- масса длины стержня. Тогда элементарный момент инерции 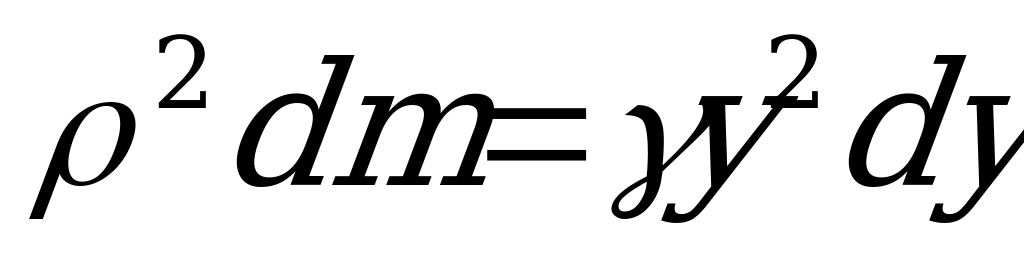 . Просуммируем их по всей длине стержня, т.е. в пределах от
. Просуммируем их по всей длине стержня, т.е. в пределах от 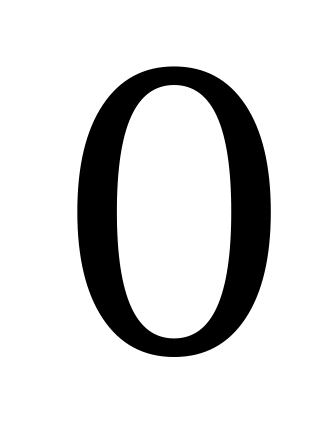 до
до 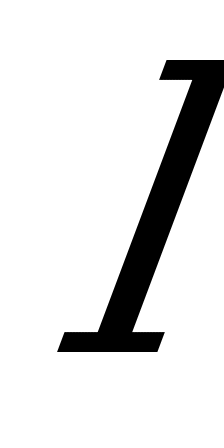 :
:
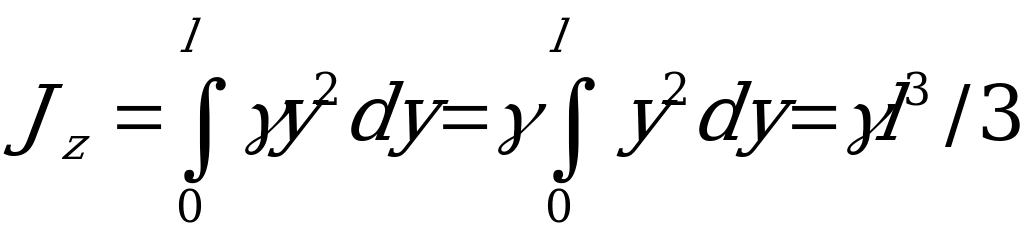 .
.
Подставим вместо 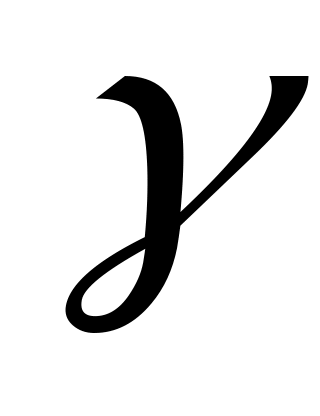 ее значение
ее значение 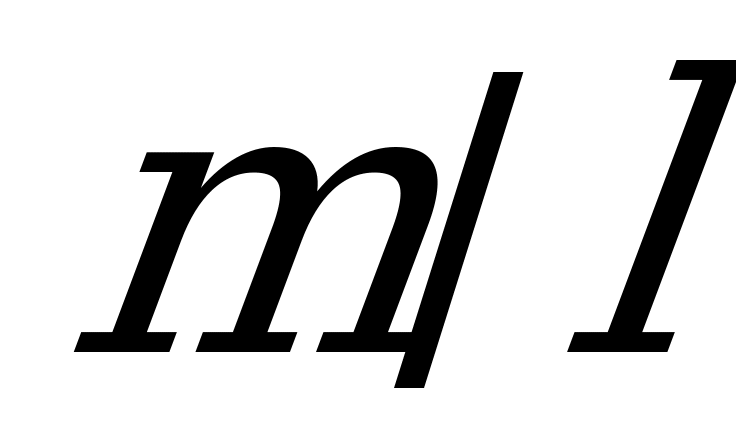 и получим окончательно
и получим окончательно
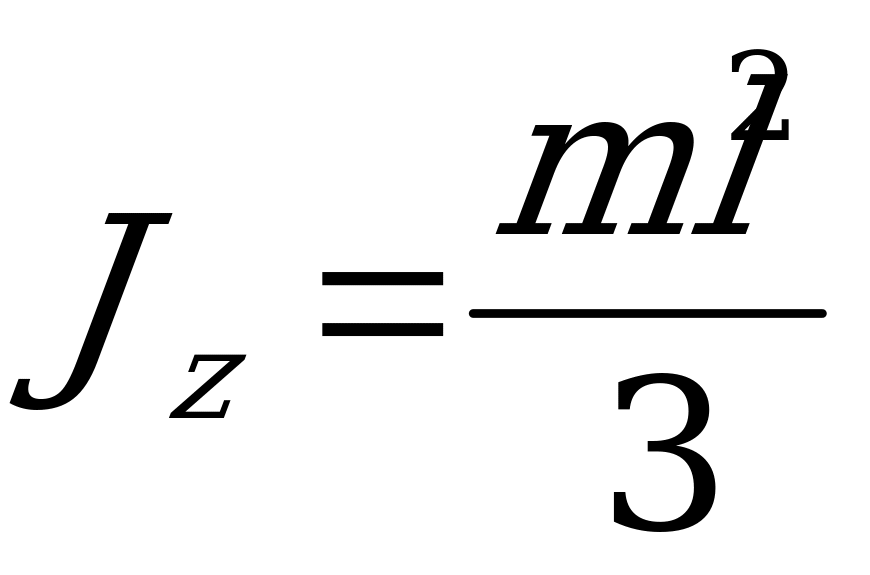 . (1.212)
. (1.212)
Момент инерции этого же стержня относительно оси 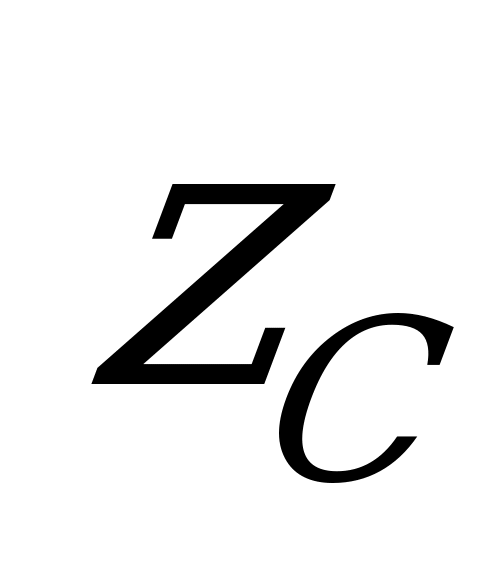 , проходящей через середину стержня (1.177).
, проходящей через середину стержня (1.177).
 zx
zx

 y dy dm
y dy dm

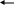











c
l/2 l/2


1.177
Ось 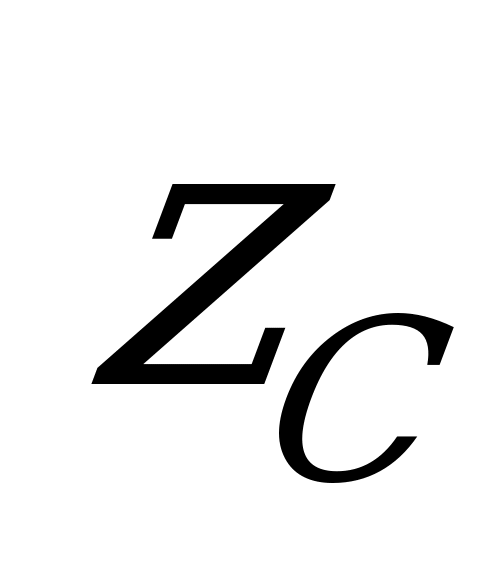 называется центральной, так как проходит через центр тяжести тела. Поступаем так же, как и в предыдущем случае, и получаем то же значение элементарного момента инерции, но при суммировании их по всей длине стержня получим
называется центральной, так как проходит через центр тяжести тела. Поступаем так же, как и в предыдущем случае, и получаем то же значение элементарного момента инерции, но при суммировании их по всей длине стержня получим
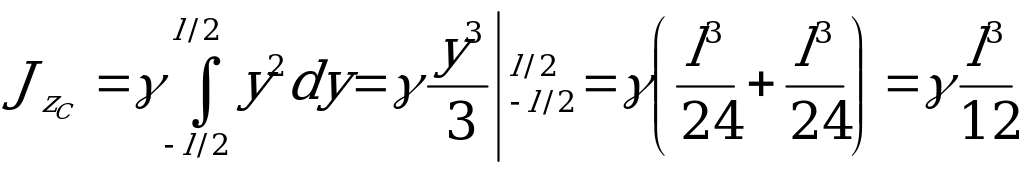 .
.
Помня, что 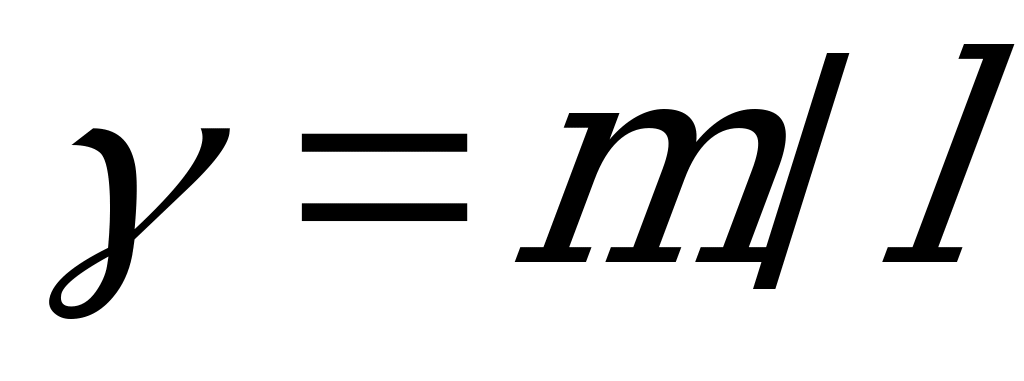 , окончательно имеем
, окончательно имеем
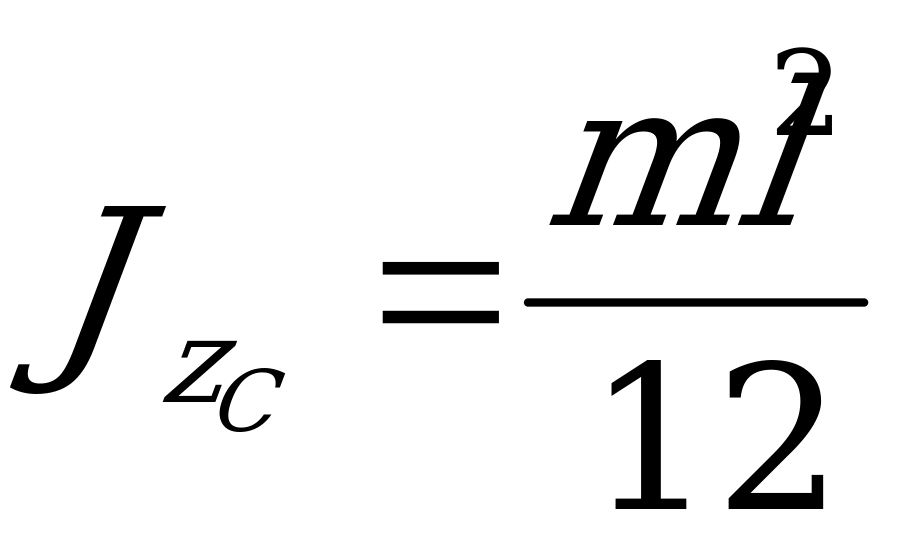 . (1.213)
. (1.213)
Для момента инерции тела относительно оси, параллельной центральной, существует зависимость – теорема Гюйгенса
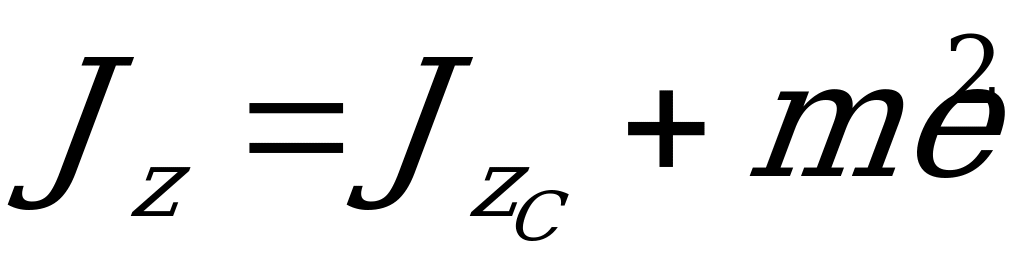 , (1.214)
, (1.214)
где  - момент инерции относительно данной оси;
- момент инерции относительно данной оси; 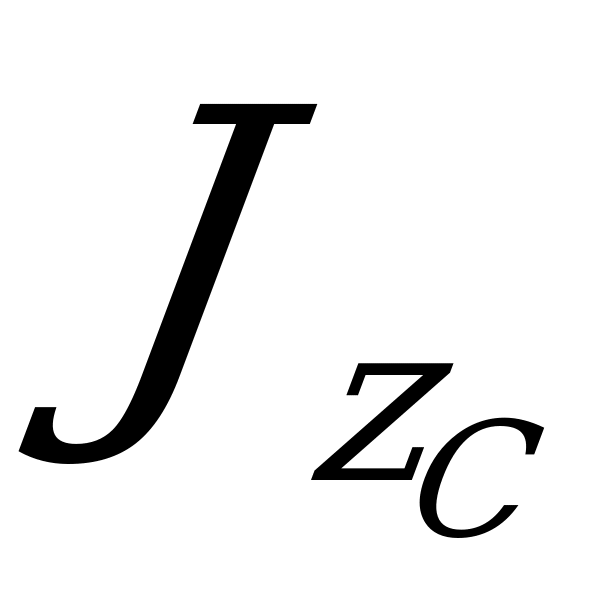 - момент инерции относительно центральной оси, параллельной данной;
- момент инерции относительно центральной оси, параллельной данной; 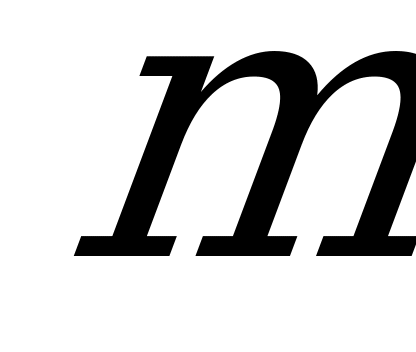 - масса тела;
- масса тела;  - расстояние между осями.
- расстояние между осями.
Зная формулу 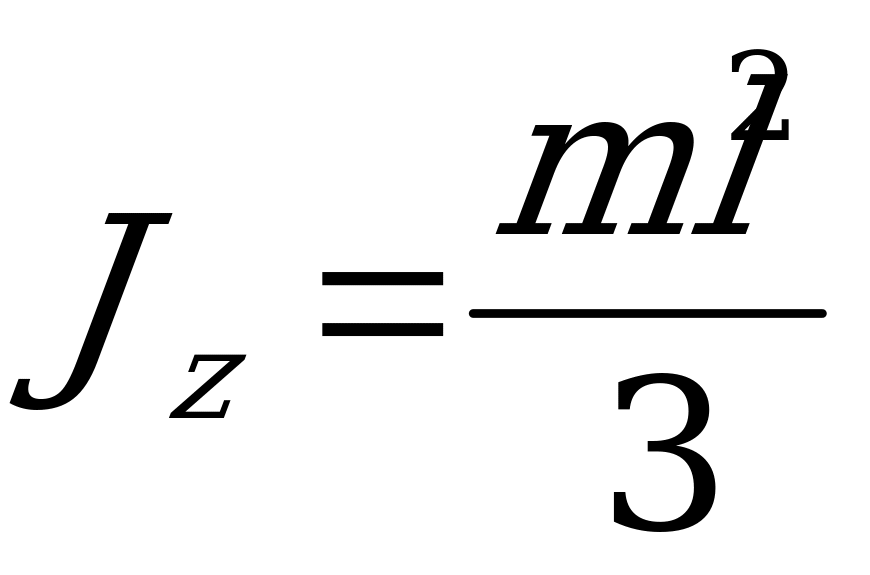 и используя зависимость (1.214) при
и используя зависимость (1.214) при 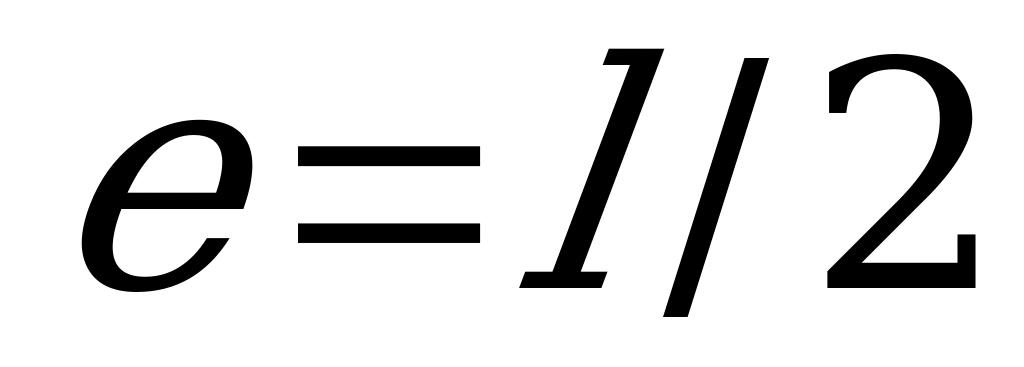 , можно получить формулу (1.213).
, можно получить формулу (1.213).
Момент инерции тонкой круглой однородной пластинки радиуса 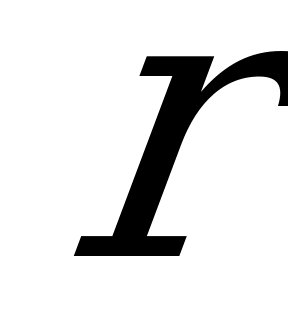 и массы
и массы 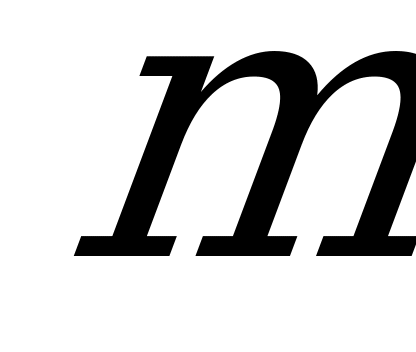 относительно центральной оси
относительно центральной оси 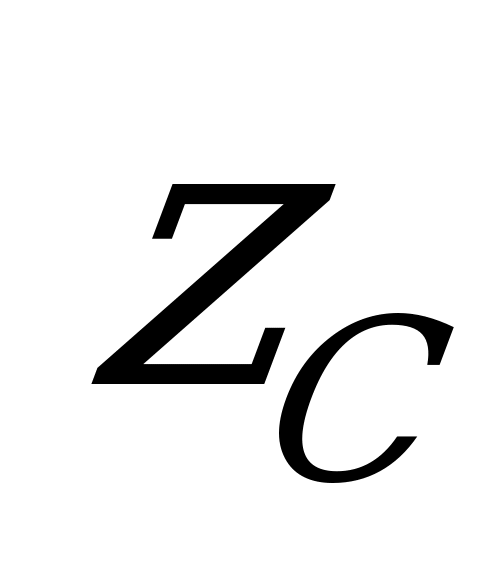 , перпендикулярной плоскости пластинки (1.178).
, перпендикулярной плоскости пластинки (1.178).
 zC
zC
dm





 c
c  y dy
y dy
r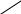 1.178
1.178

Выделим в пластинке элемент массой 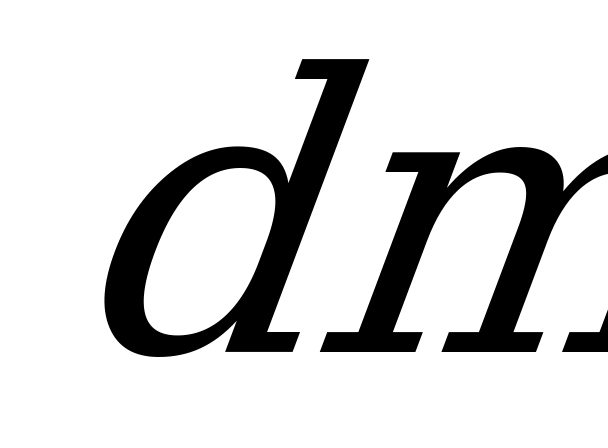 в виде кольца радиуса
в виде кольца радиуса 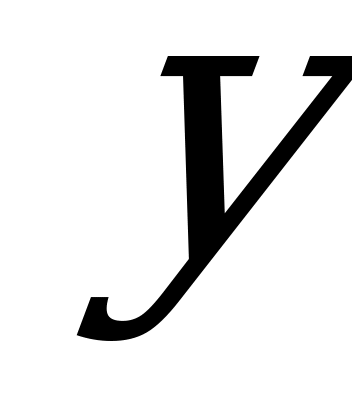 и шириной
и шириной 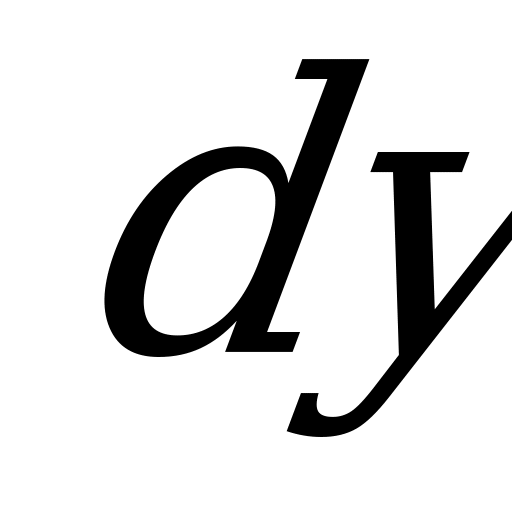 . Площадь кольца ввиду малости
. Площадь кольца ввиду малости 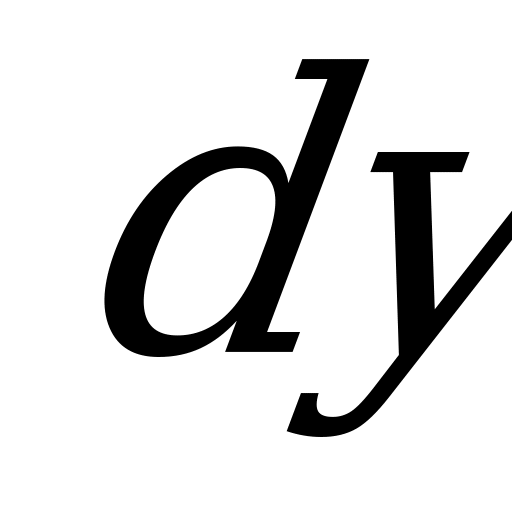 можно принять равной
можно принять равной 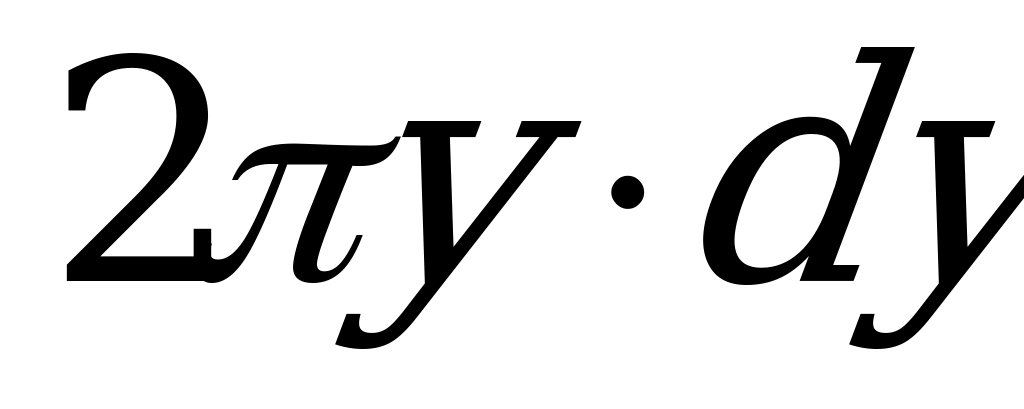 . Тогда элементарная масса
. Тогда элементарная масса 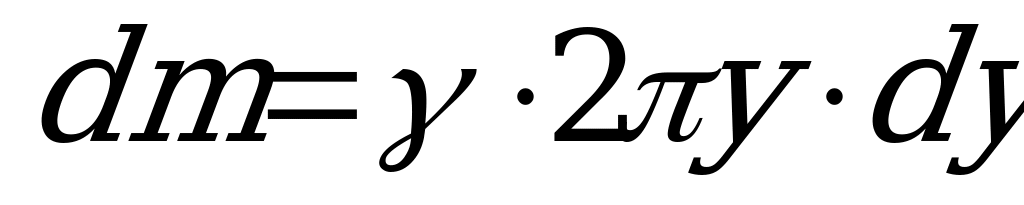 , где
, где 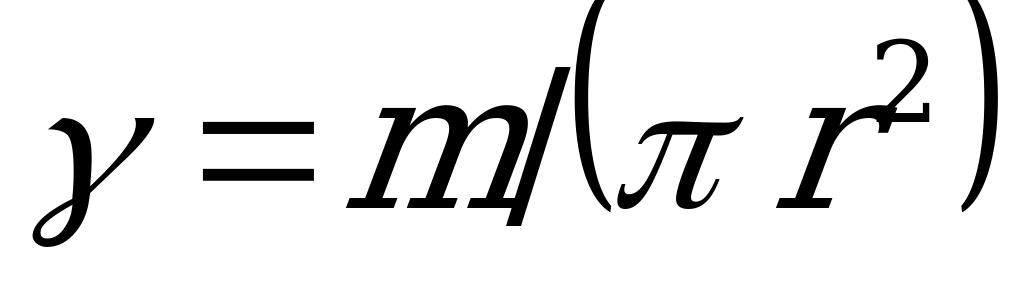 - масса единицы всей площади пластинки. Просуммируем элементарные моменты инерции пластинки
- масса единицы всей площади пластинки. Просуммируем элементарные моменты инерции пластинки 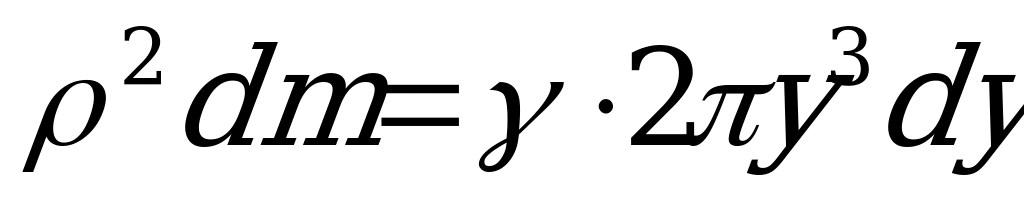 по всей площади, т.е. в пределах от
по всей площади, т.е. в пределах от 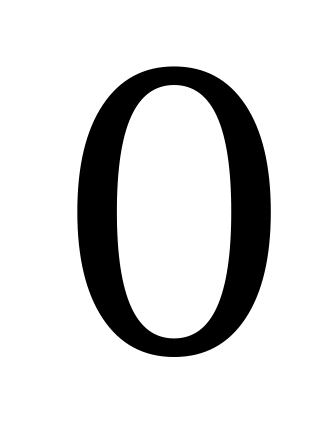 до
до 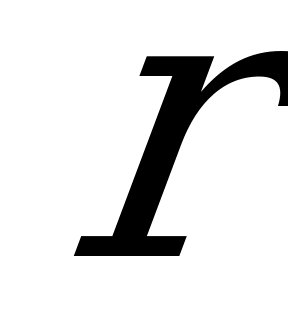 :
:
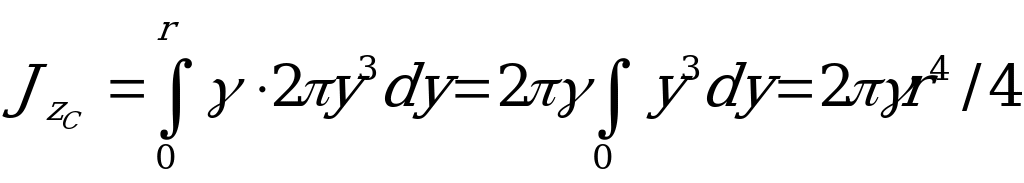 .
.
Заменим 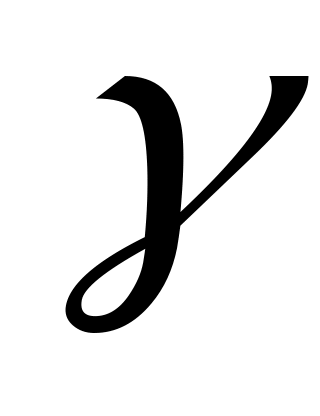 ее значением
ее значением 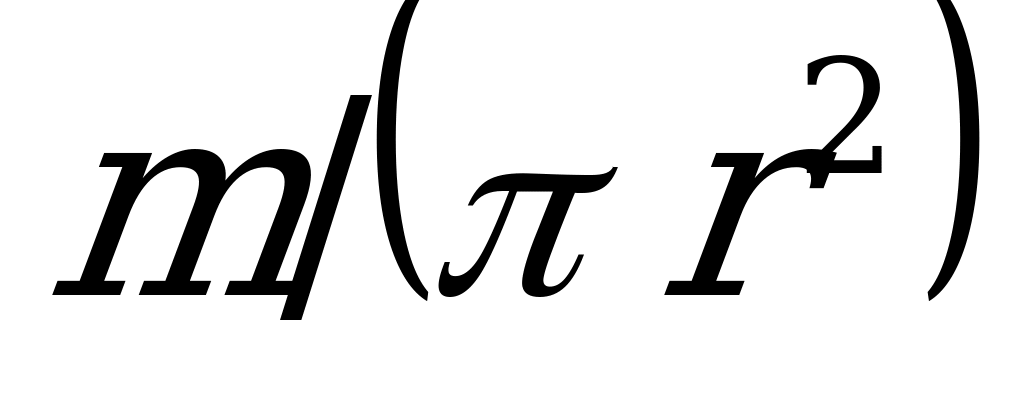 и получим
и получим
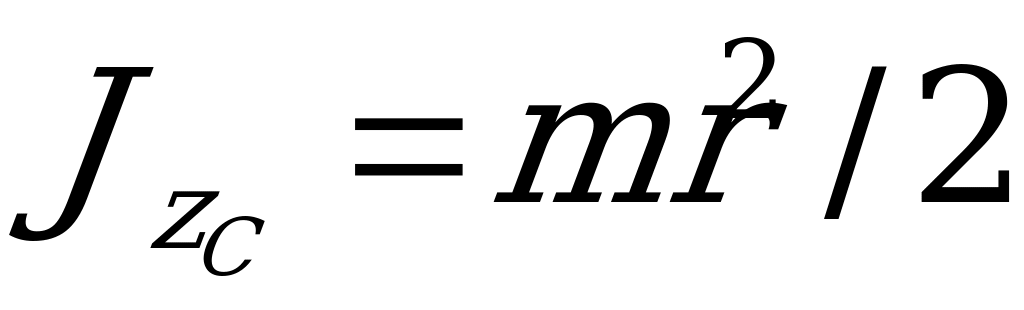 . (1.215)
. (1.215)
Если ввести в эту формулу диаметр диска 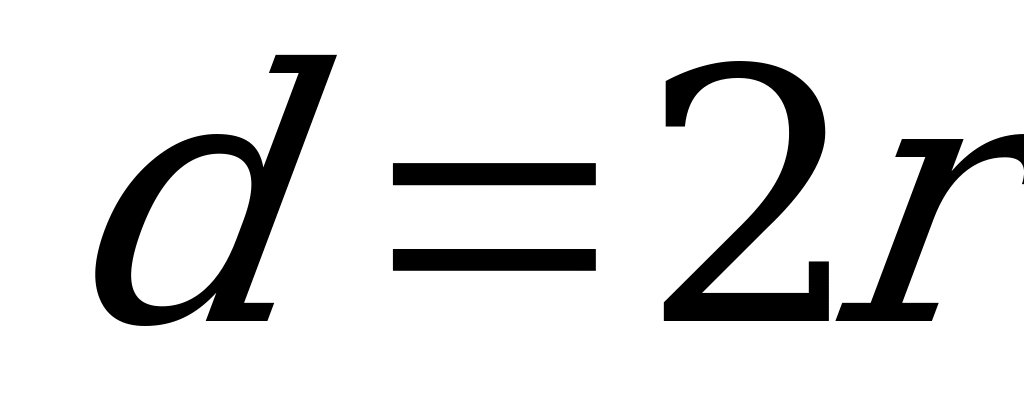 , то получим
, то получим
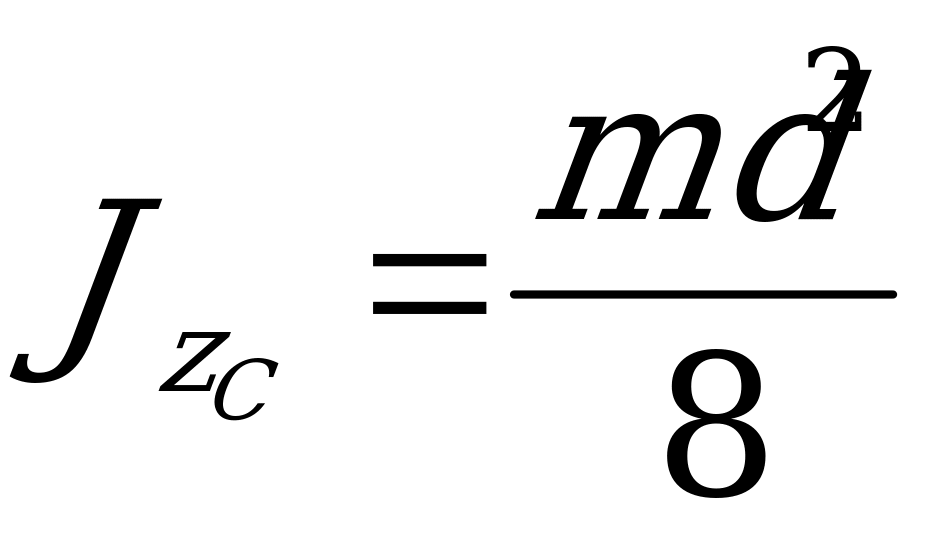 . (1.216)
. (1.216)
Кручение круглого прямого бруса.
Одинаковые предпосылки и формулы.
Деформация бруса при кручении характеризуется величиной
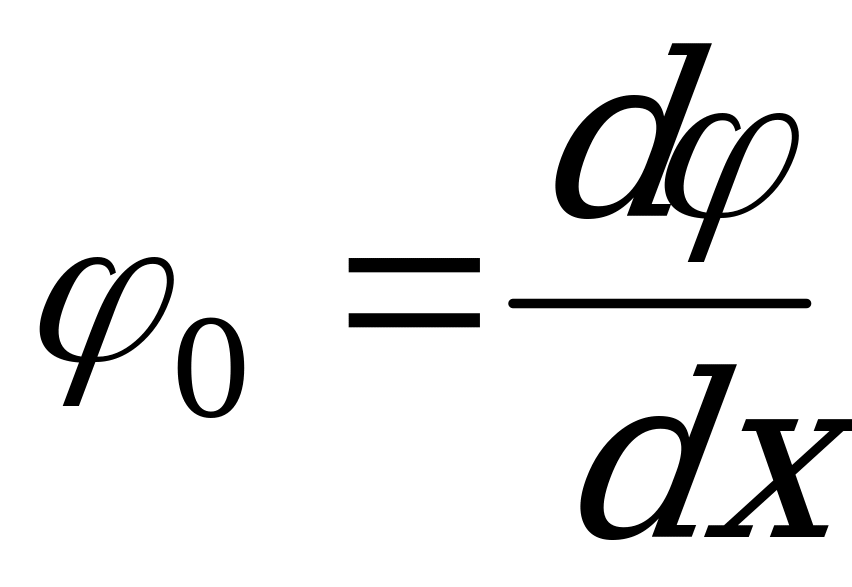 , (2.30)
, (2.30)
называемой относительным углом закручивания. Это угол взаимного поворота двух сечений, отнесенный к расстоянию между ними.
Если у поверхности выделенного элемента вырезать слой 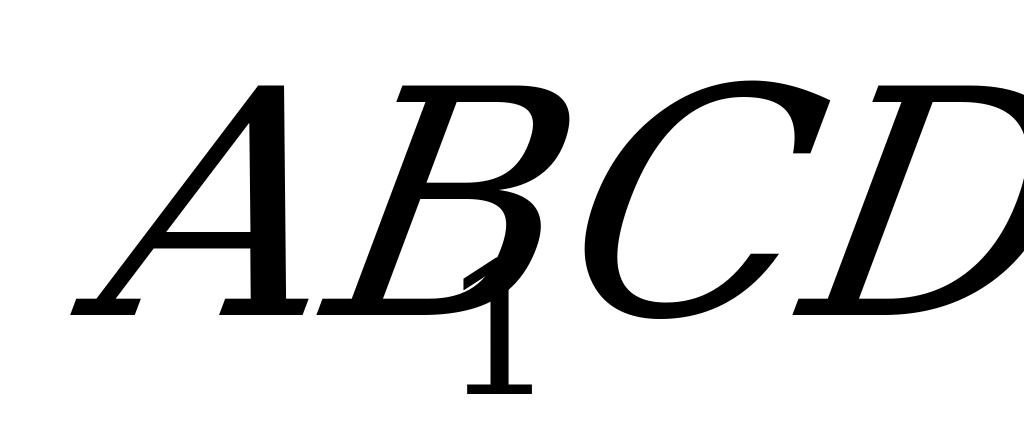 , который из-за малости размеров можно считать призмой, то этот призматический элемент находится в состоянии чистого сдвига, т.е.
, который из-за малости размеров можно считать призмой, то этот призматический элемент находится в состоянии чистого сдвига, т.е. 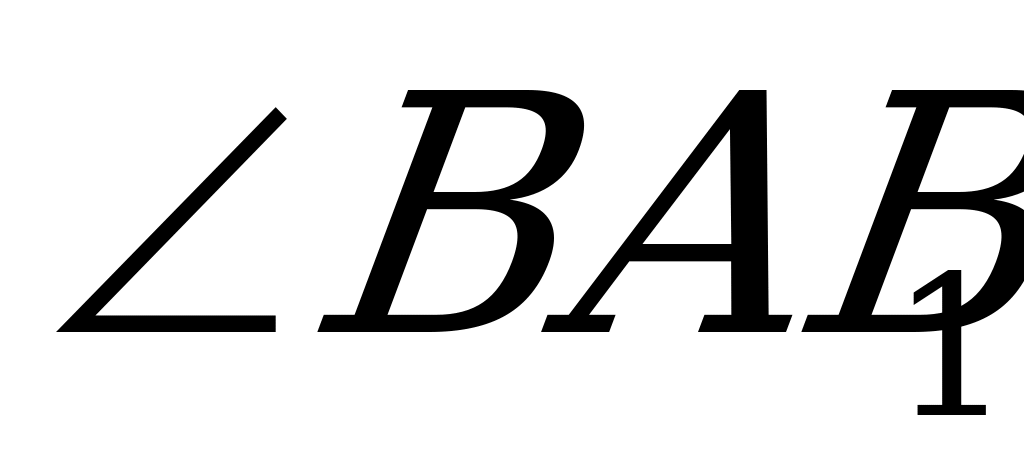 на цилиндрической поверхности элемента является углом сдвига
на цилиндрической поверхности элемента является углом сдвига 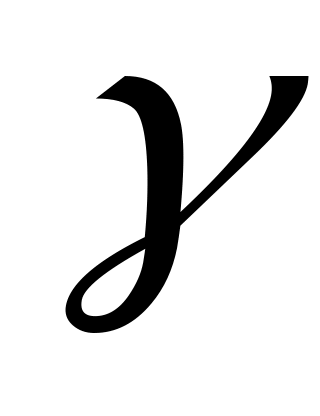 . Приближенно можно считать
. Приближенно можно считать 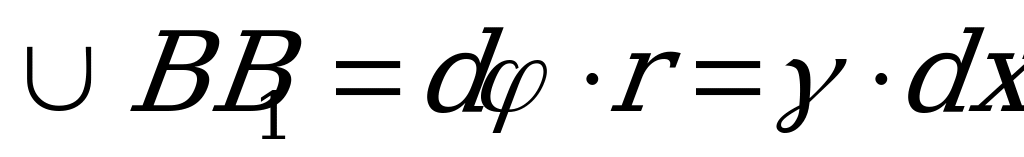 , отсюда с учетом равенства (2.30)
, отсюда с учетом равенства (2.30)
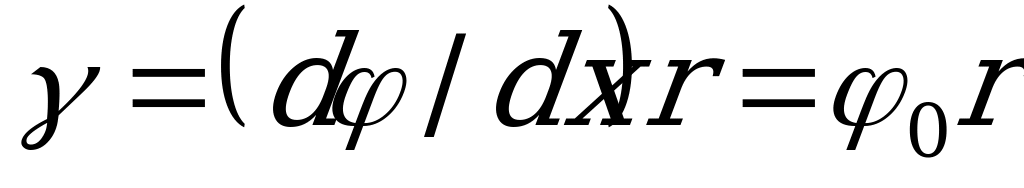 . (2.31)
. (2.31)
Чтобы выразить максимальные касательные напряжения 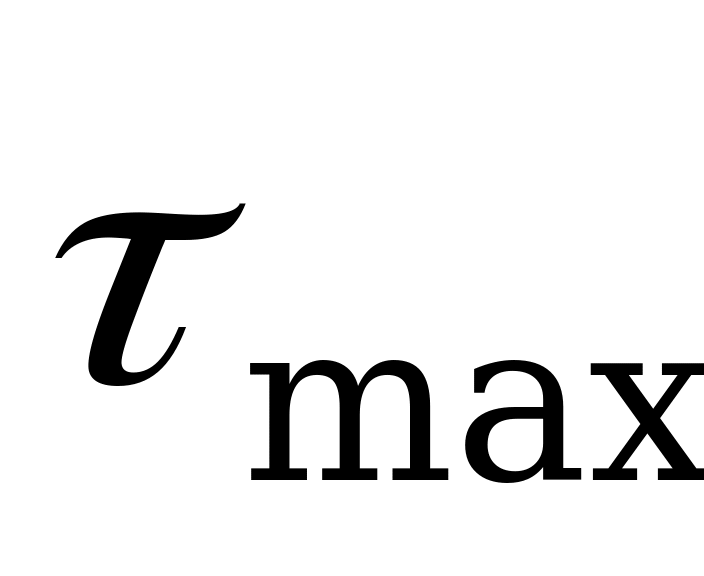 в крайних точках поперечного сечения бруса, найденное значение
в крайних точках поперечного сечения бруса, найденное значение 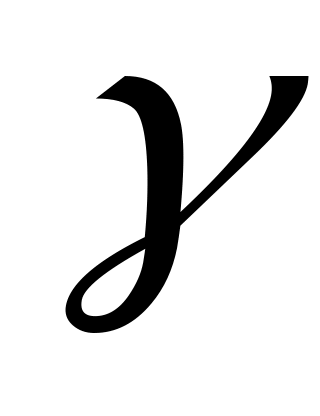 подставим в выражение
подставим в выражение 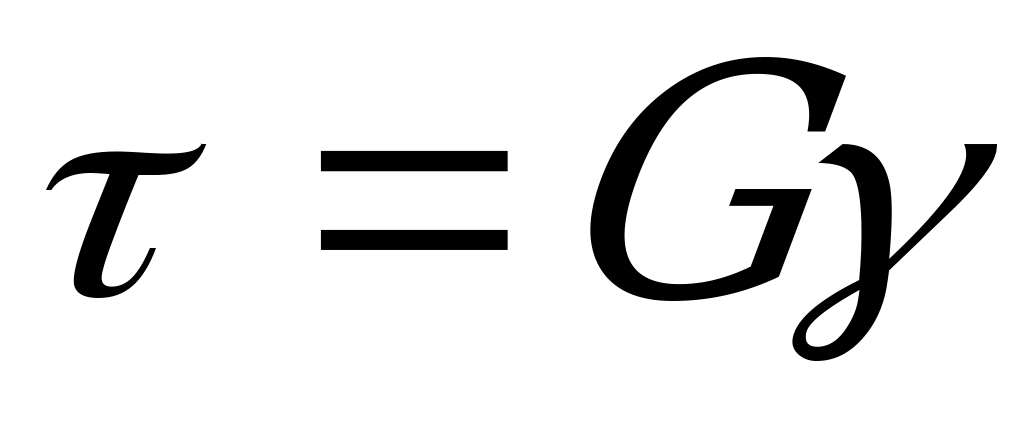 :
:
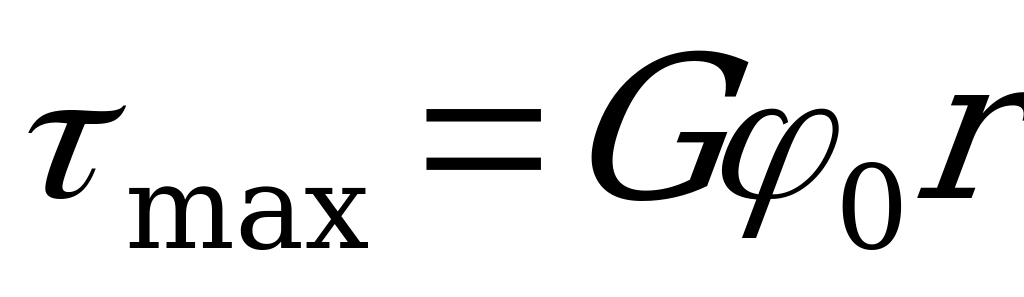 . (2.32)
. (2.32)
Если мысленно вырезать призматический элемент на расстоянии 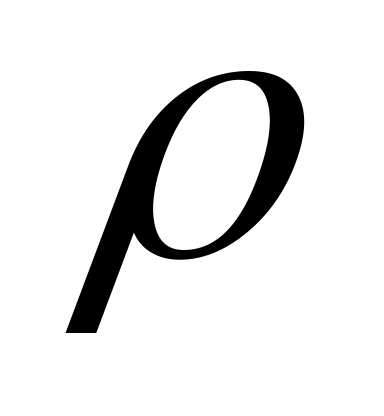 от оси бруса, то угол сдвига у этого элемента
от оси бруса, то угол сдвига у этого элемента 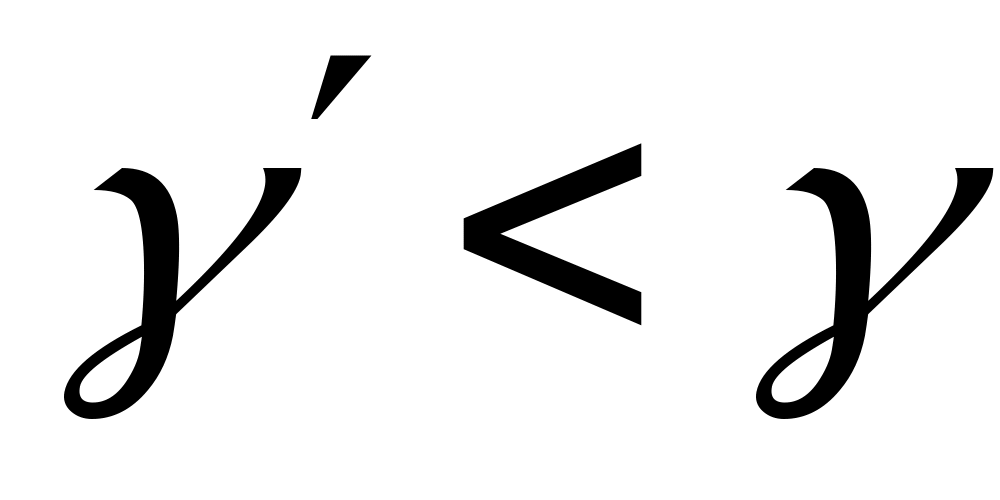 и тогда в любой точке поперечного сечения на расстоянии
и тогда в любой точке поперечного сечения на расстоянии 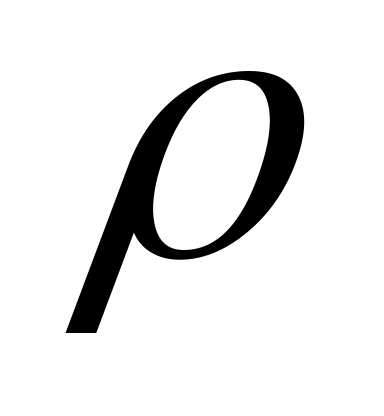 от центра
от центра
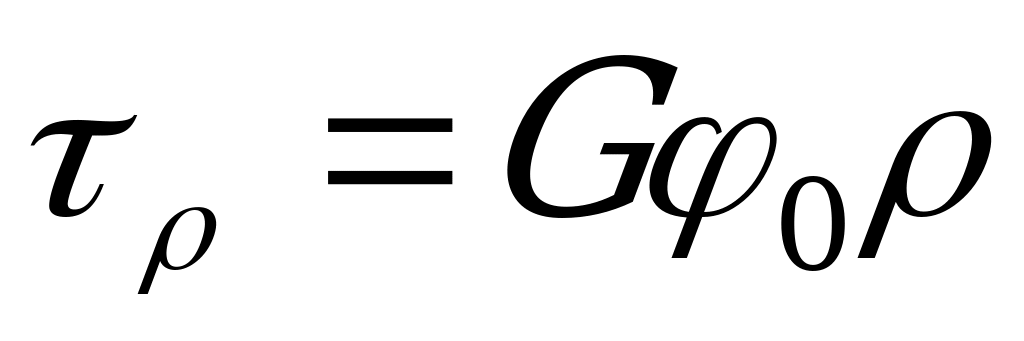 . (2.33)
. (2.33)
Равенство (2.33) выражает линейный закон распределения касательных напряжений по поперечному сечению при кручении. Максимальные касательные напряжения кручения 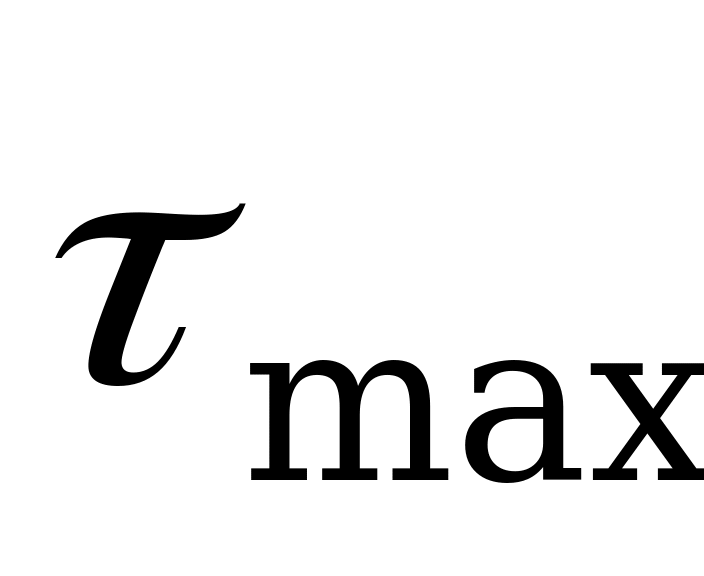 возникают у края сечения, а по мере приближения к центру убывают до нуля. Таким образом, в большей степени сопротивляются кручению те части бруса, которые расположены ближе к его поверхности. Поэтому для экономии материала брусья, работающие на кручение, иногда изготовляют пустотелыми. Поперечное сечение такого бруса для полого вала имеет форму плоского кругового кольца, распределение касательных напряжений в нем показано на рис. 2.45, б.
возникают у края сечения, а по мере приближения к центру убывают до нуля. Таким образом, в большей степени сопротивляются кручению те части бруса, которые расположены ближе к его поверхности. Поэтому для экономии материала брусья, работающие на кручение, иногда изготовляют пустотелыми. Поперечное сечение такого бруса для полого вала имеет форму плоского кругового кольца, распределение касательных напряжений в нем показано на рис. 2.45, б.
2.45 2.46
Касательные напряжения вследствие закона парности возникают и в продольных сечениях бруса(2.46).
Зная закон распределения касательных напряжений по сечению, установим зависимость между возникшим в нем крутящим моментом 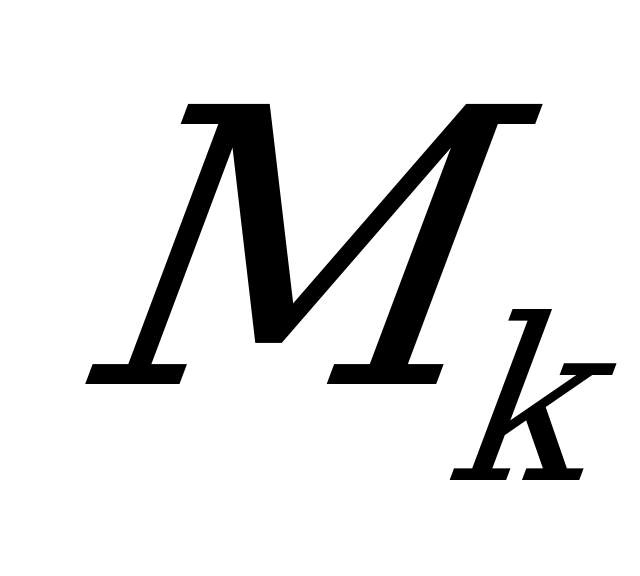 , относительным углом закручивания
, относительным углом закручивания 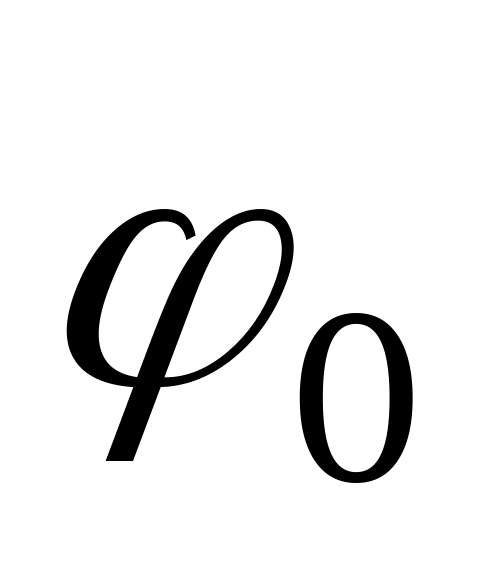 и максимальными касательными напряжениями
и максимальными касательными напряжениями 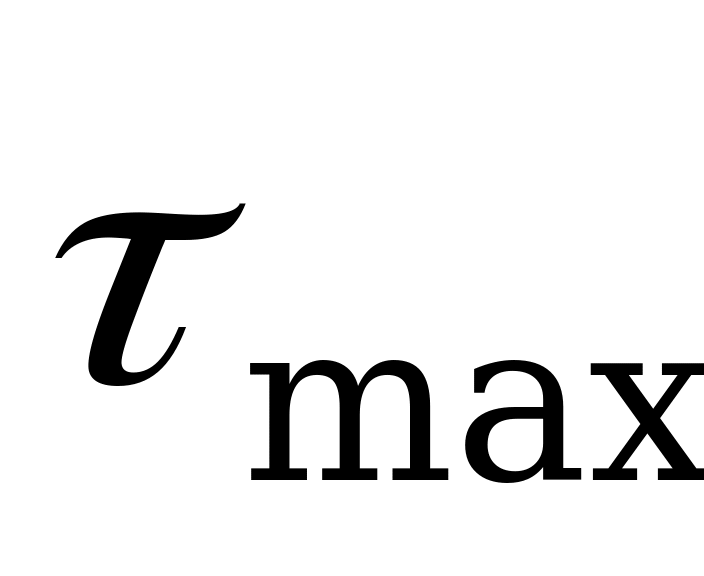 .
.
Пусть в некотором сечении (2.47,а) возник крутящийся момент 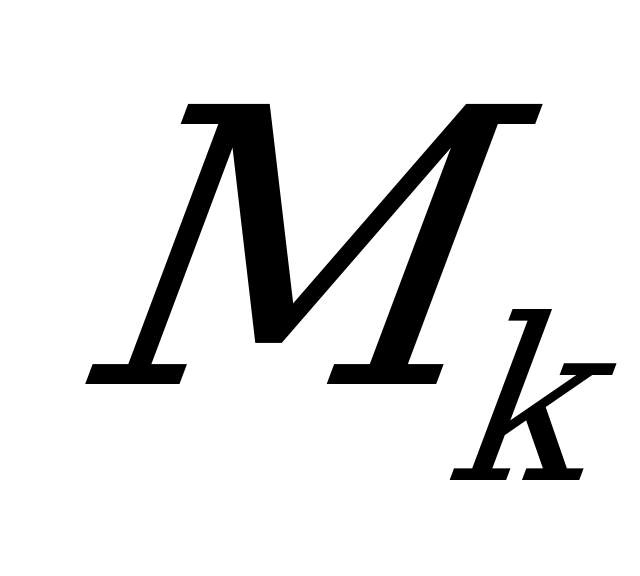 , который как известно, можно определить через внешние моменты. На некотором расстоянии
, который как известно, можно определить через внешние моменты. На некотором расстоянии 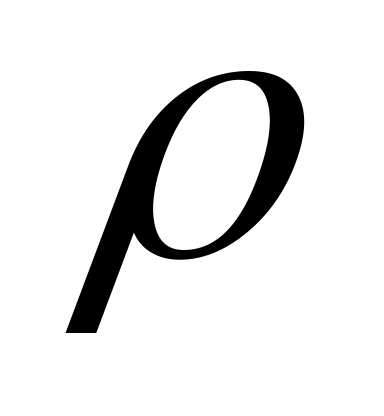 от центра выберем в сечении бесконечно малую площадку
от центра выберем в сечении бесконечно малую площадку  и допустим, что напряжение по этой площадке
и допустим, что напряжение по этой площадке 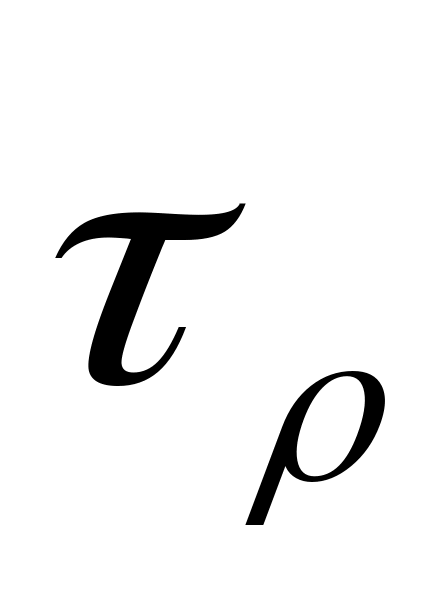 . Тогда с учетом равенства
. Тогда с учетом равенства 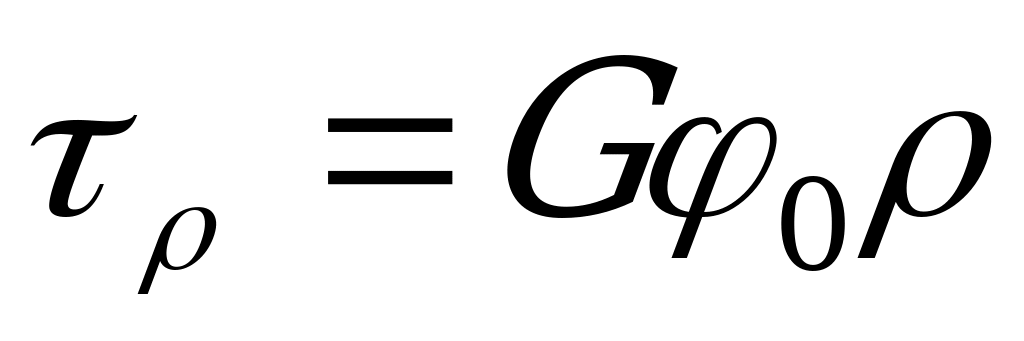 элементарный крутящий момент
элементарный крутящий момент
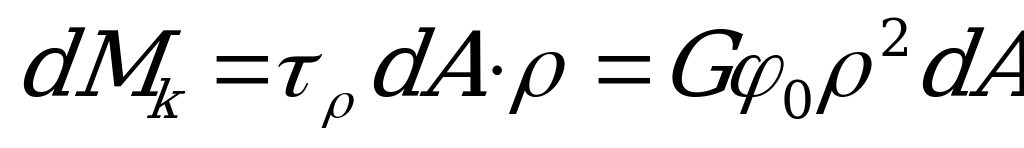 .
.
а) б)
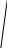

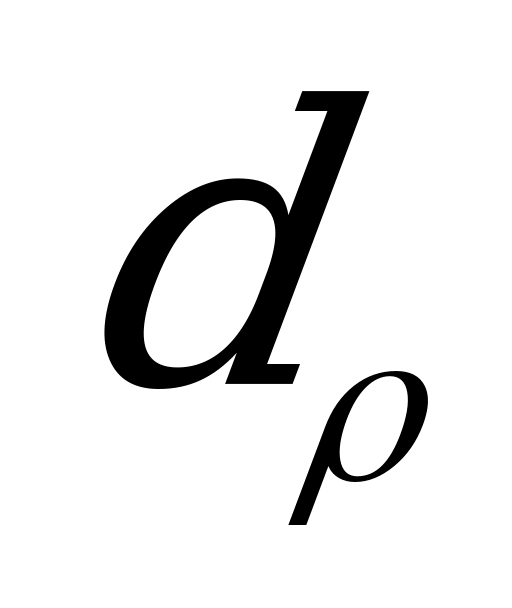


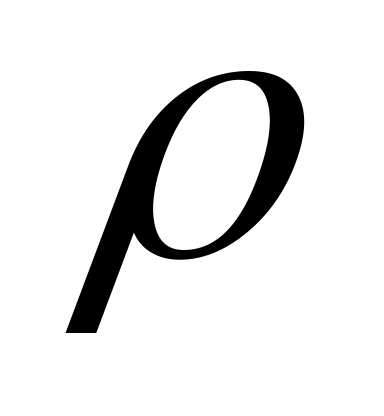




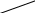

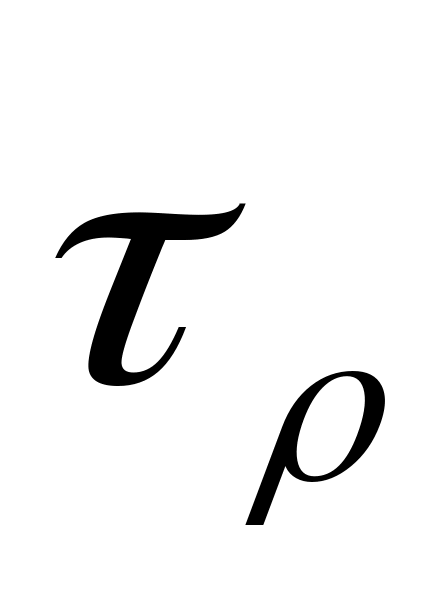
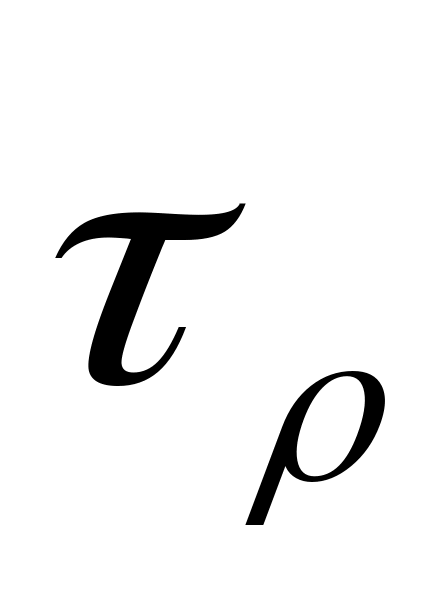
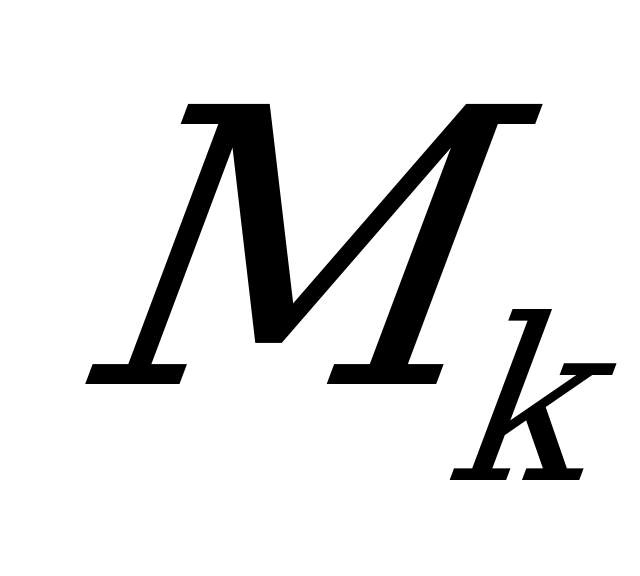


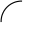

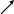






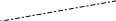



2.47
Суммируя элементарные крутящиеся моменты 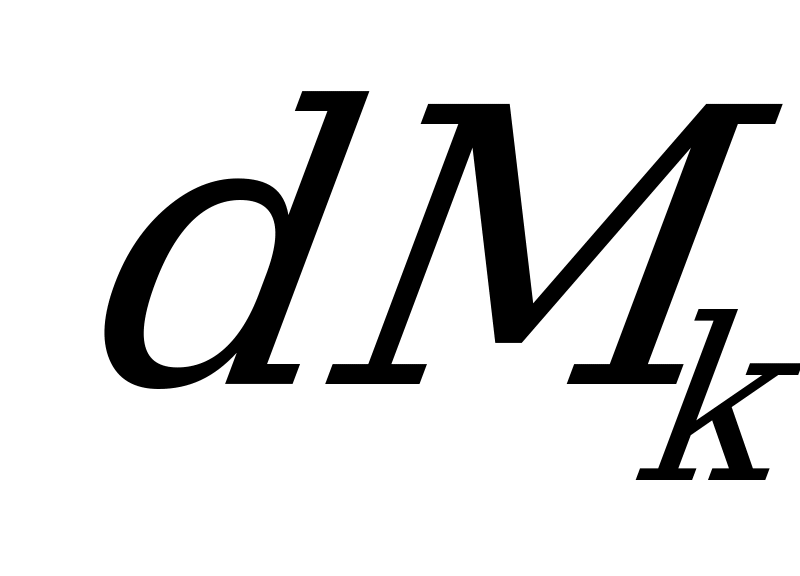 по всей площади и учитывая, что
по всей площади и учитывая, что 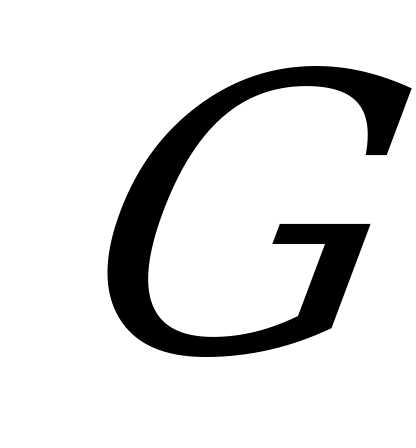 и
и 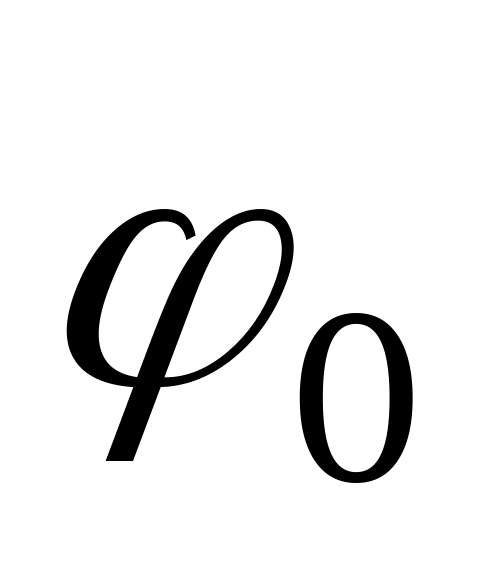 - величины постоянные, получаем
- величины постоянные, получаем
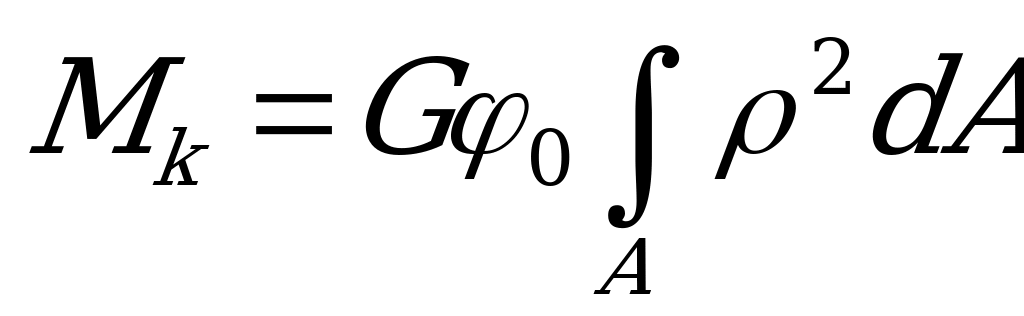 .
.
Обозначив 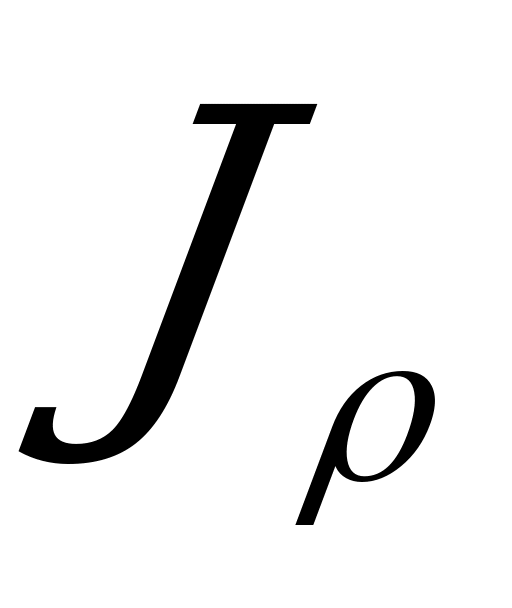 выражение
выражение 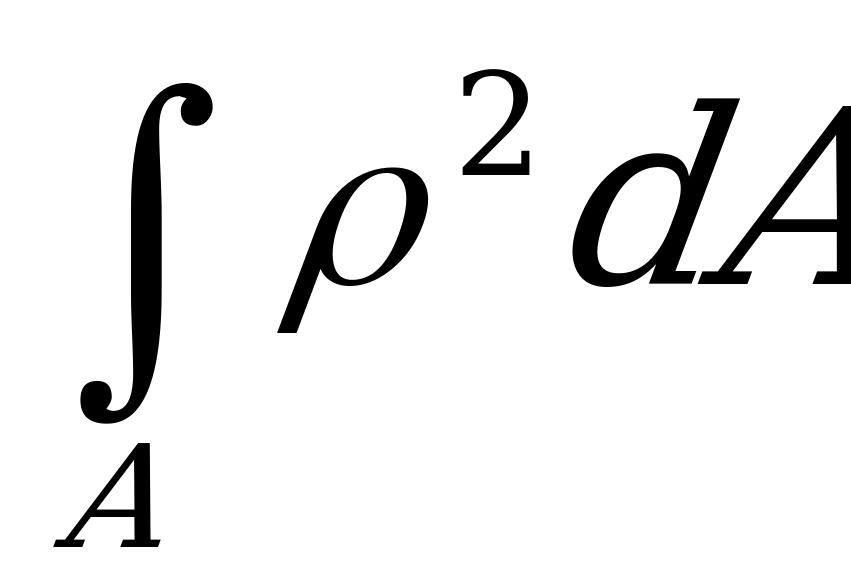 , получим
, получим
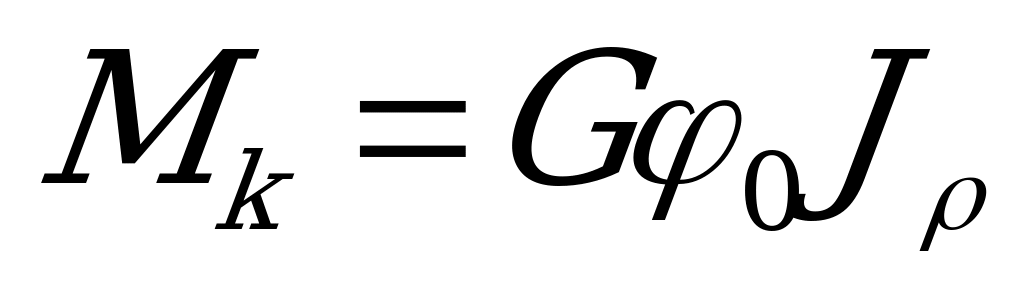 . (2.34)
. (2.34)
Величина
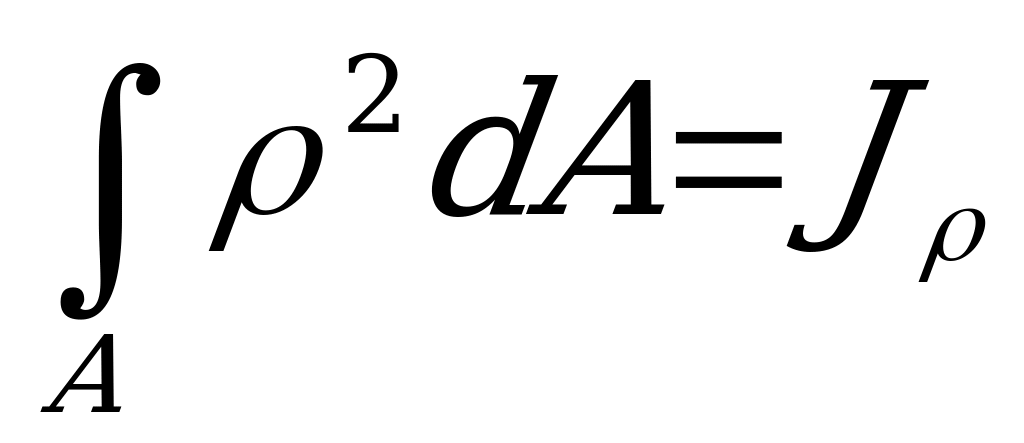 , (2.35)
, (2.35)
т.е. сумма произведений всех элементарных площадок поперечного сечения на квадраты их расстояний от центра, называется полярным моментом инерции сечения.
В уравнении 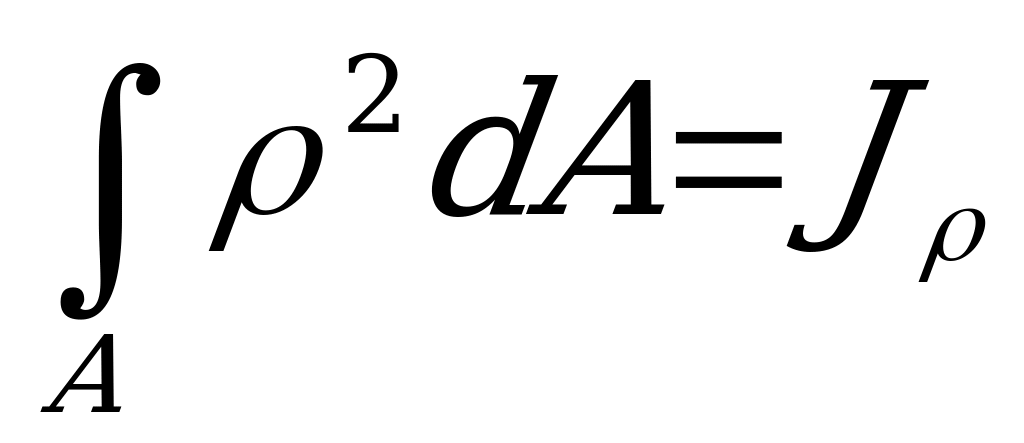
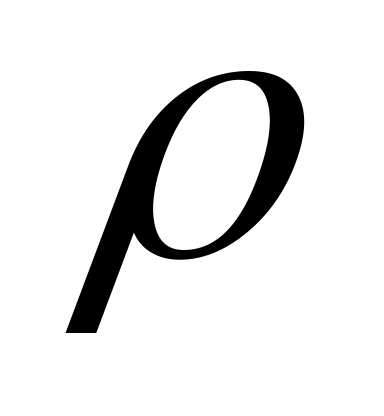 выражается в м, см или мм, а
выражается в м, см или мм, а  - в м2, см2 или мм2; следовательно, полярный момент инерции выражается в м4, см4 или мм4.
- в м2, см2 или мм2; следовательно, полярный момент инерции выражается в м4, см4 или мм4.
Из равенства 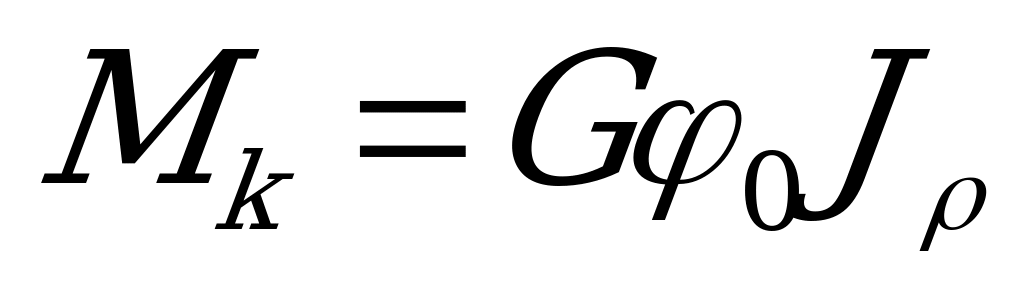 получаем выражение относительного угла закручивания
получаем выражение относительного угла закручивания
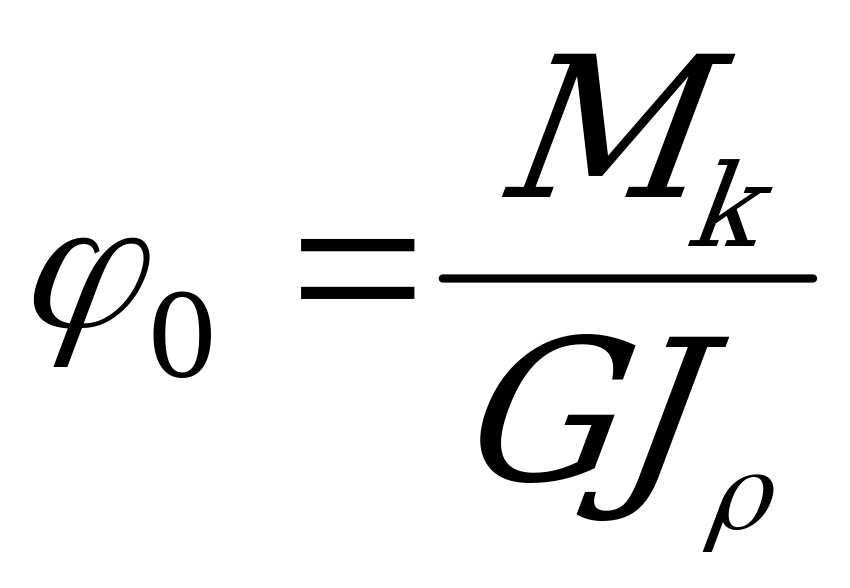 . (2.36)
. (2.36)
Полный угол закручивания бруса (значение углового перемещения при кручении)
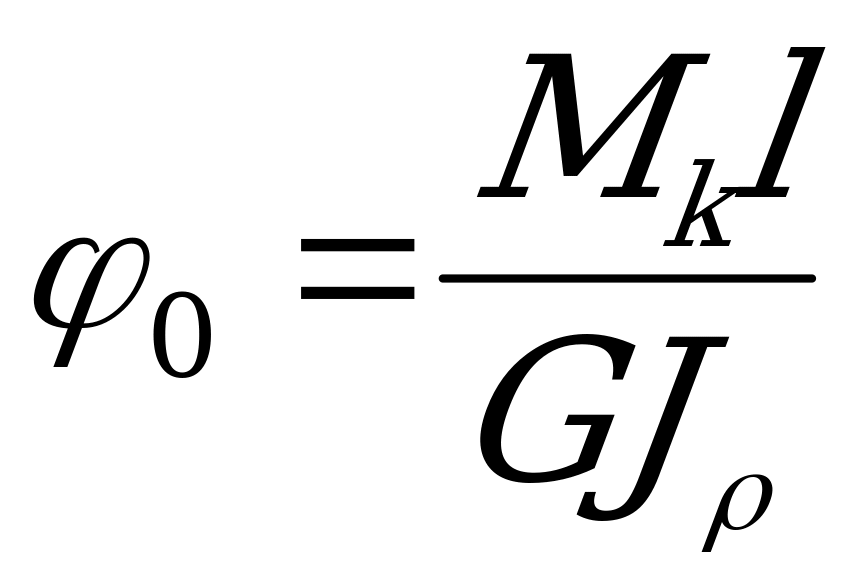 . (2.37)
. (2.37)
Легко видеть, что эта формула в принципе аналогична формуле 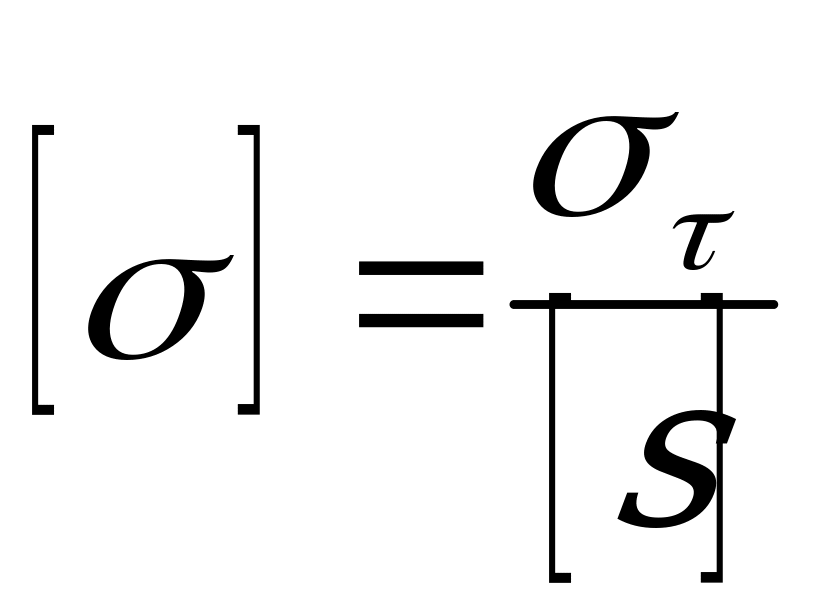 для удлинения
для удлинения 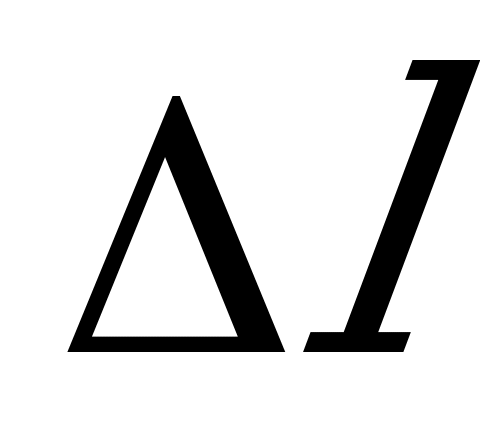 . Произведение
. Произведение 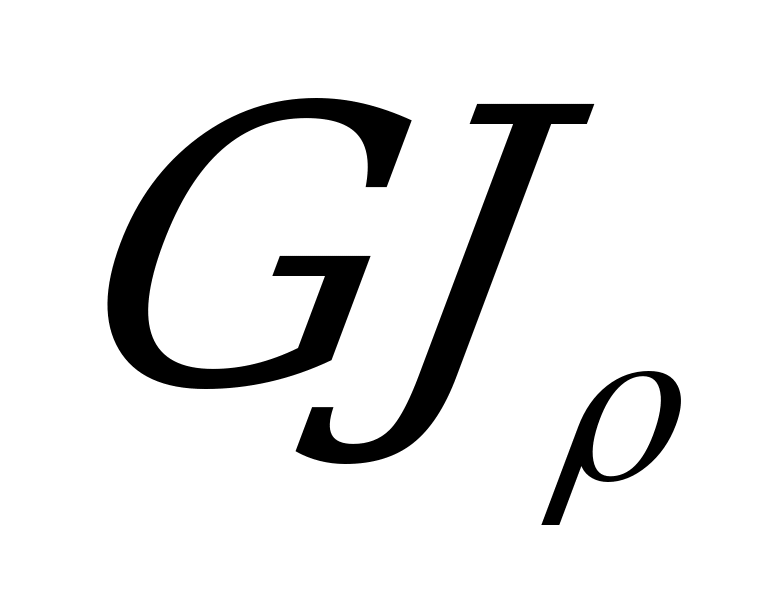 называется жесткостью сечения бруса при кручении.
называется жесткостью сечения бруса при кручении.
В формуле (2.36) 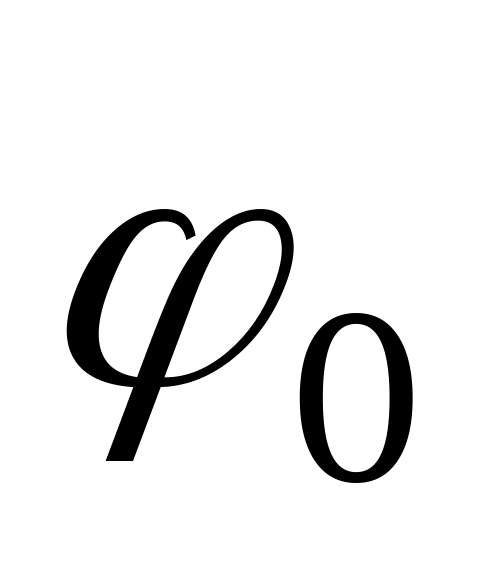 выражается в рад/м или рад/мм, в формуле (2.37)
выражается в рад/м или рад/мм, в формуле (2.37) 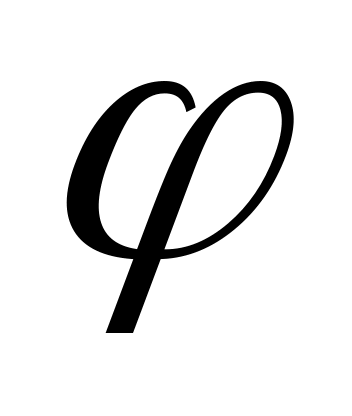 выражается в рад.
выражается в рад.
Заменив в равенстве 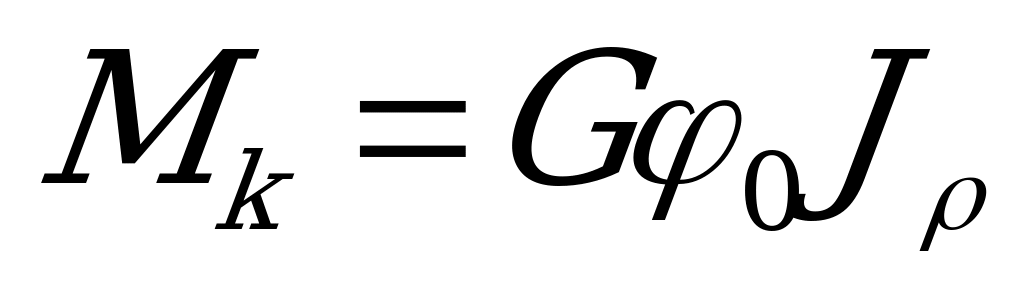 произведение
произведение 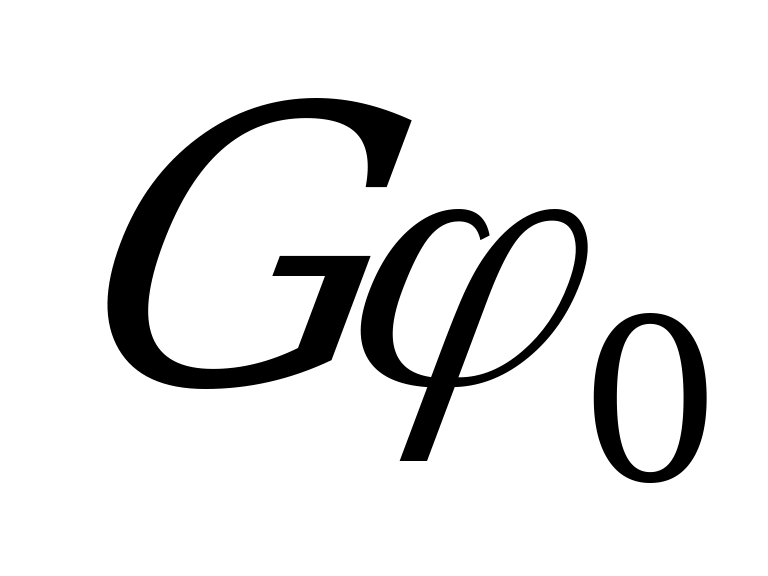 его выражение из формулы
его выражение из формулы 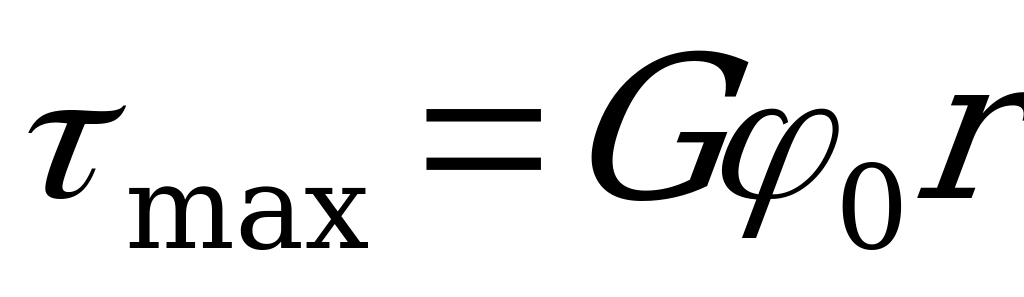 , получим
, получим 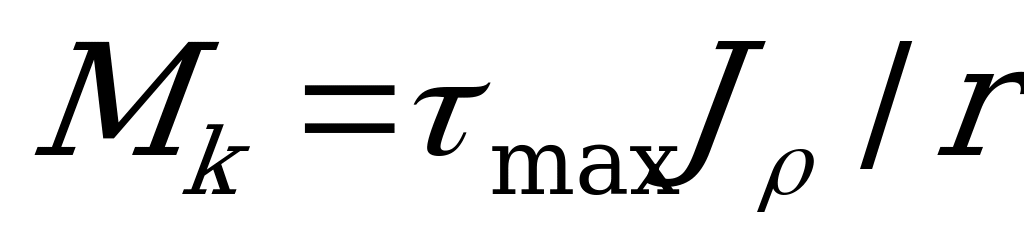 . Откуда максимальные касательные напряжения
. Откуда максимальные касательные напряжения
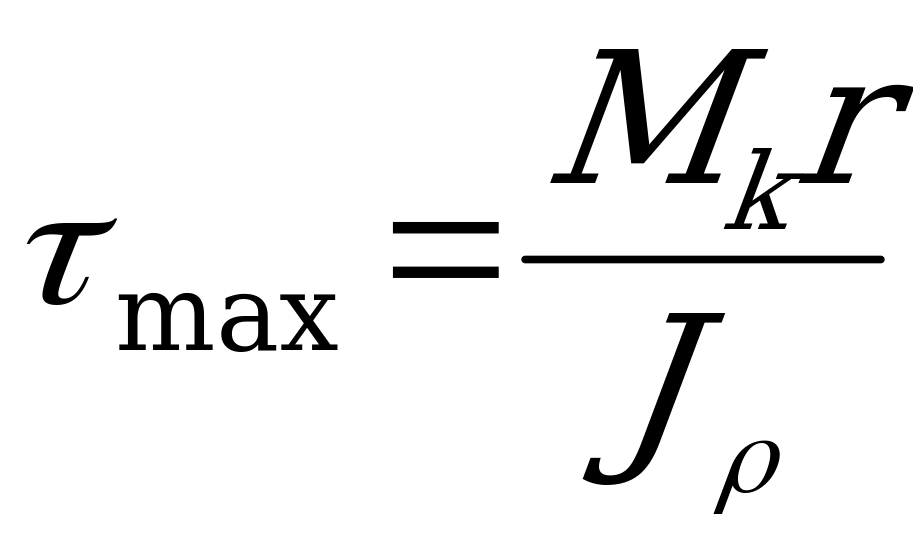 . (2.38)
. (2.38)
Отношение полярного момента инерции круглого сечения в его радиусу называется полярным моментом сопротивления и обозначается 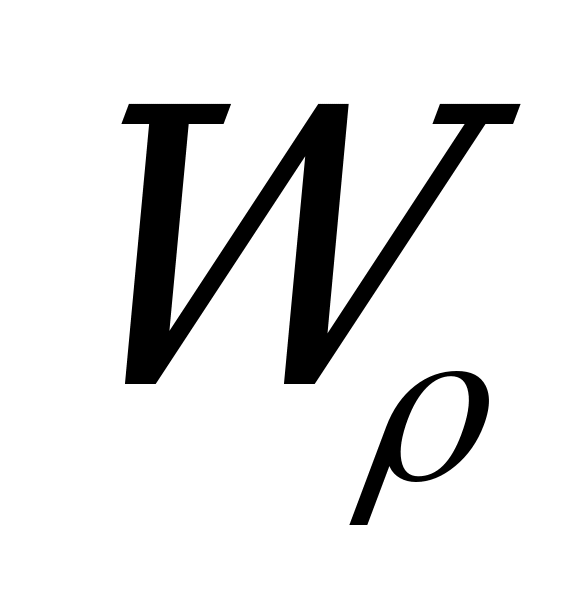 :
:
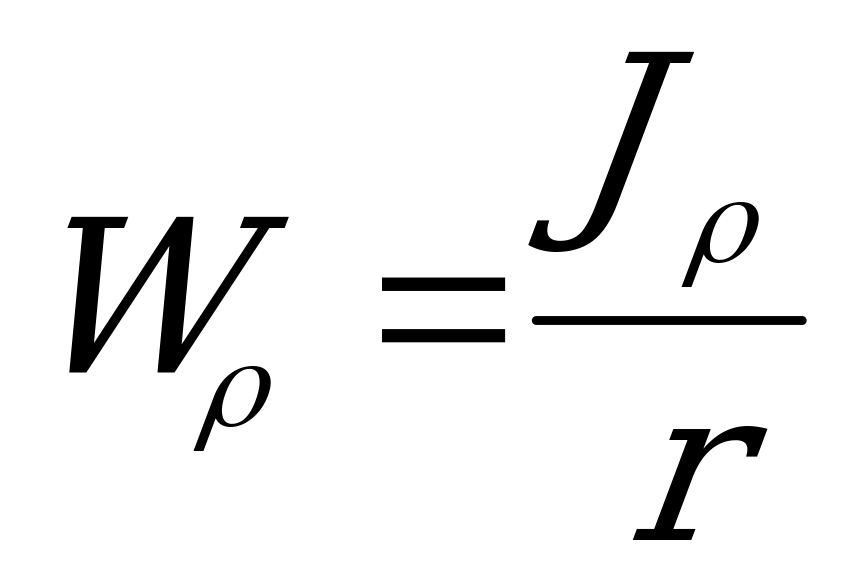 , (2.39)
, (2.39)
где 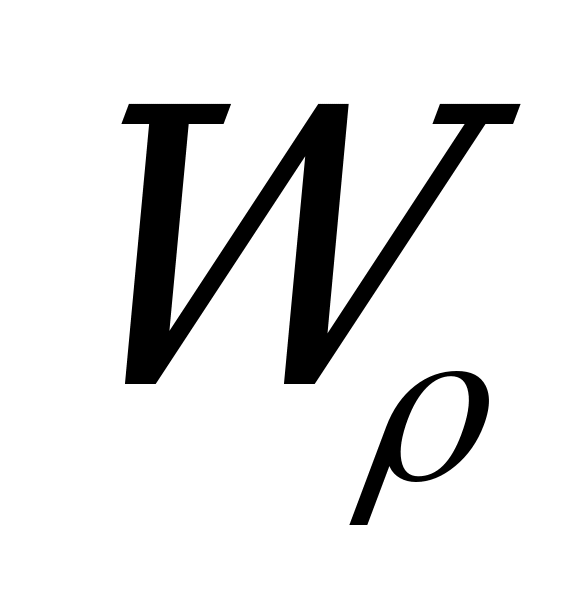 выражается в м3, см3 или мм3. Таким образом,
выражается в м3, см3 или мм3. Таким образом,
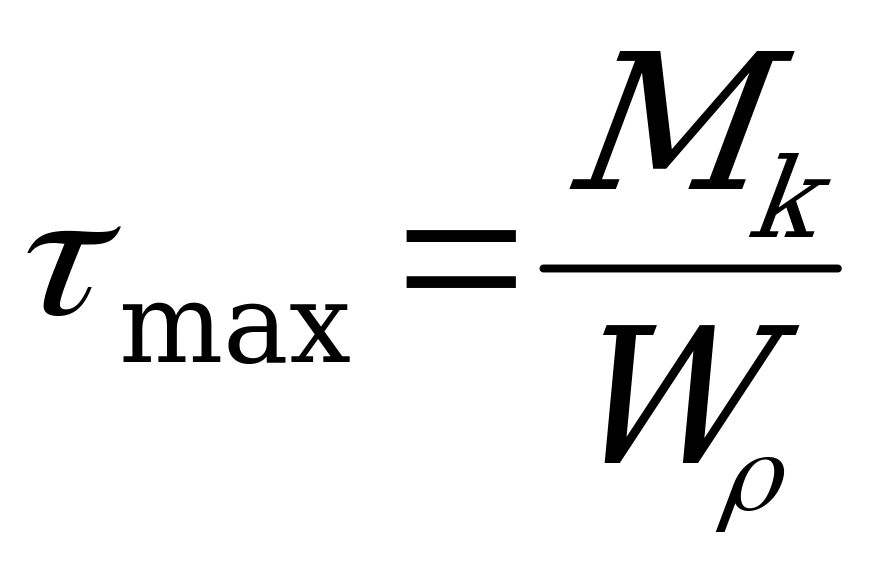 . (2.40)
. (2.40)
Максимальное касательное напряжение в поперечном сечении бруса равно частному от деления крутящего момента на полярный момент сопротивления.
При вычислении значений 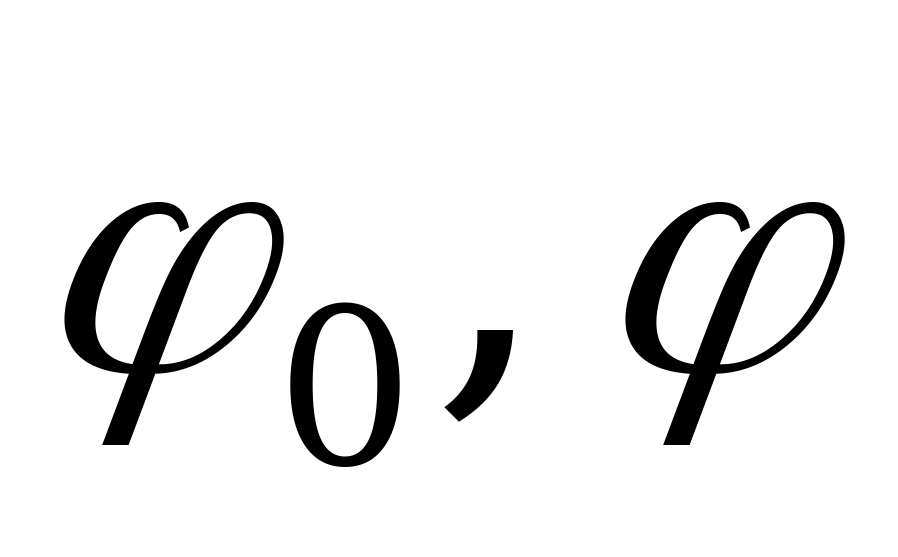 и
и 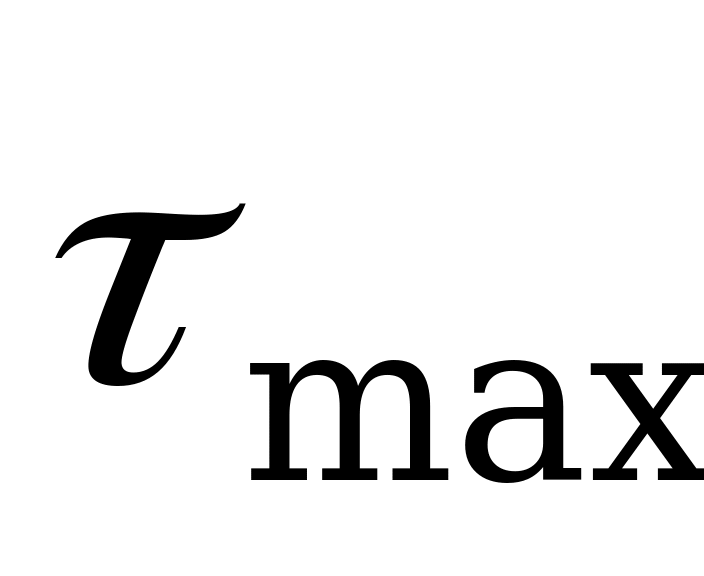 соответственно по формулам (2.36), (2.37) и (2.38) кроме крутящего момента
соответственно по формулам (2.36), (2.37) и (2.38) кроме крутящего момента 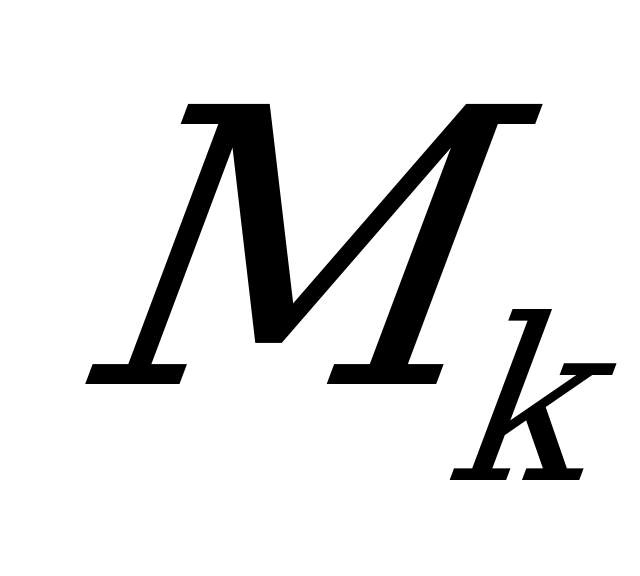 , модуля сдвига
, модуля сдвига 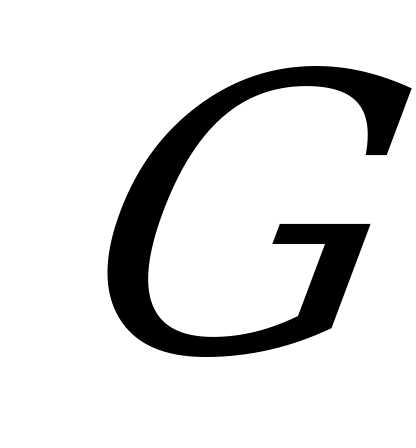 , длины
, длины 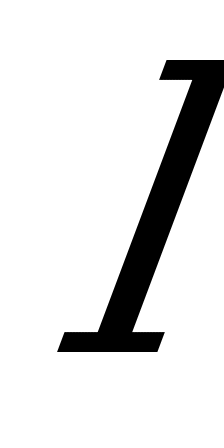 нужно знать значение полярного момента инерции
нужно знать значение полярного момента инерции 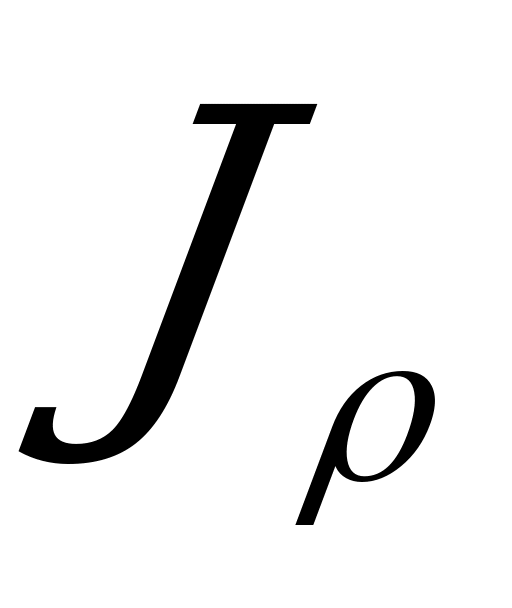 или полярного момента сопротивления
или полярного момента сопротивления 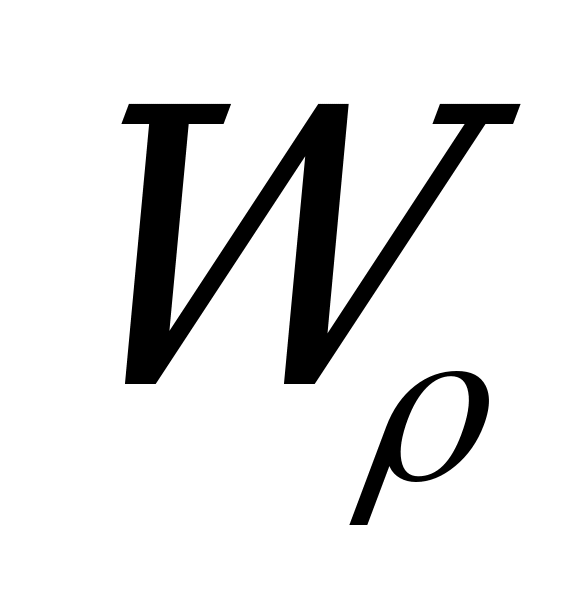 , которые зависят от формы и размеров сечения.
, которые зависят от формы и размеров сечения.
Чтобы получить формулу полярного момента инерции круга, выделим в его площади на расстоянии 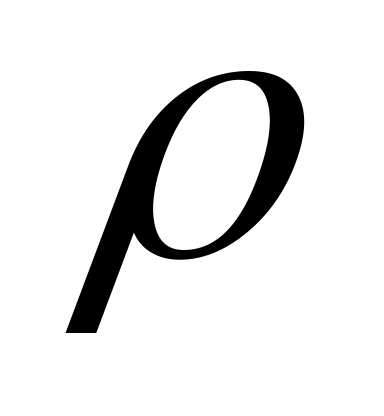 от центра элемент
от центра элемент  в виде плоского кольца шириной
в виде плоского кольца шириной  (2.47,б). Если пренебречь разницей между длинами внешнего и внутреннего контуров кольцевого элемента, то его площадь
(2.47,б). Если пренебречь разницей между длинами внешнего и внутреннего контуров кольцевого элемента, то его площадь 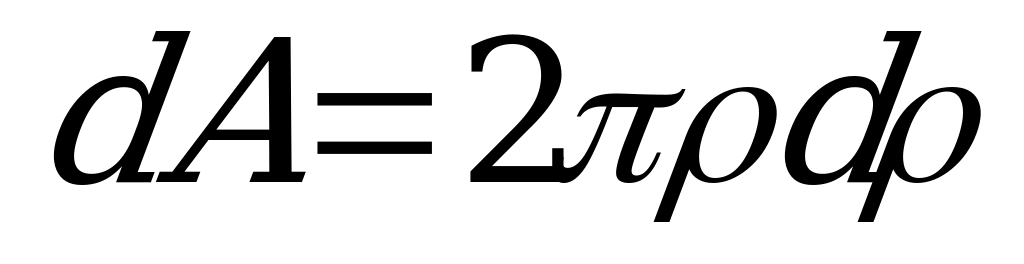 . Подставляя значение
. Подставляя значение  в выражение
в выражение 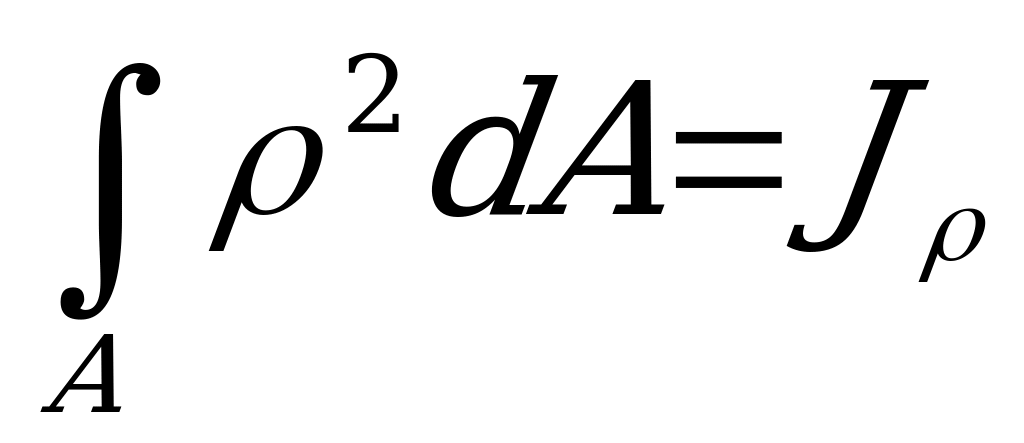 и принимая во внимание, что при интегрировании по всей площади
и принимая во внимание, что при интегрировании по всей площади 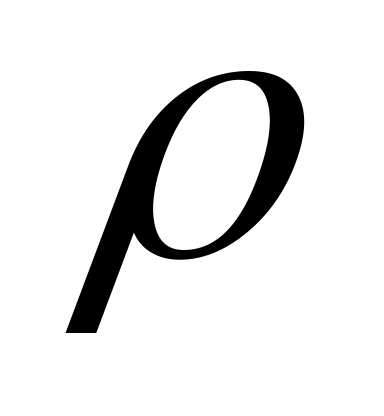 изменяется от 0 до
изменяется от 0 до 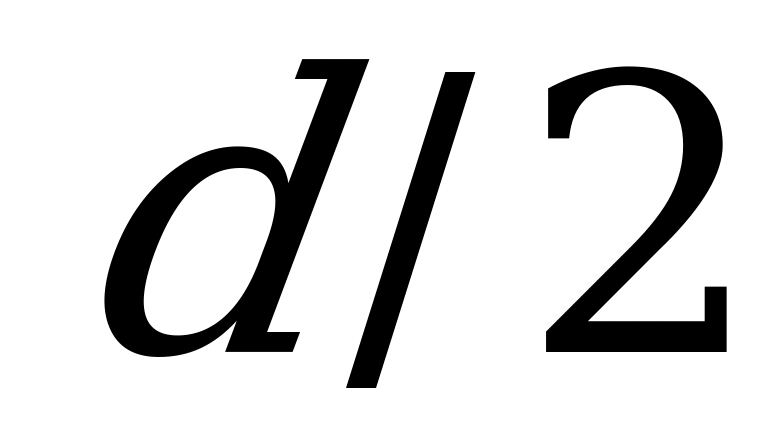 (где
(где 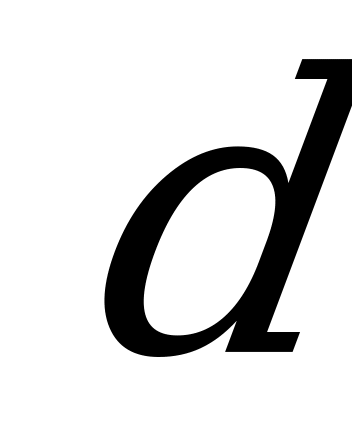 - диаметр круглого сечения), получаем
- диаметр круглого сечения), получаем
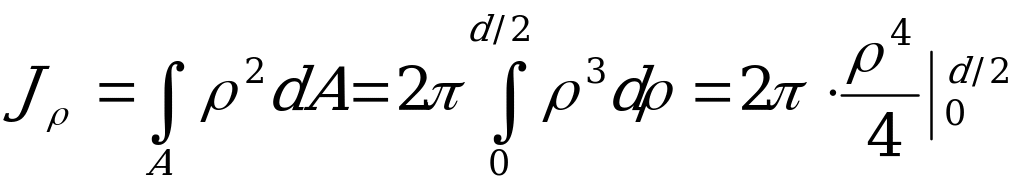 .
.
Отсюда
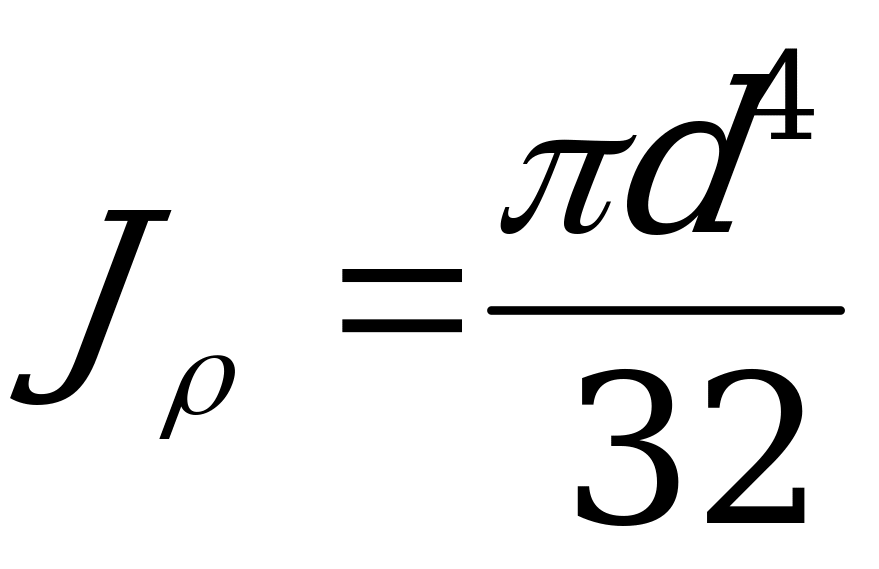 . (2.41)
. (2.41)
Момент инерции сечений
С некоторыми геометрическими характеристиками сечений мы знакомы. Любое сечение бруса имеет определенную геометрическую форму и площадь. В формулы для определения координат центра тяжести сечения входит алгебраическая сумма произведений элементарных площадей на координаты их центров тяжести; эта величина называется статическим моментом сечения. В интегральной форме статические моменты сечения 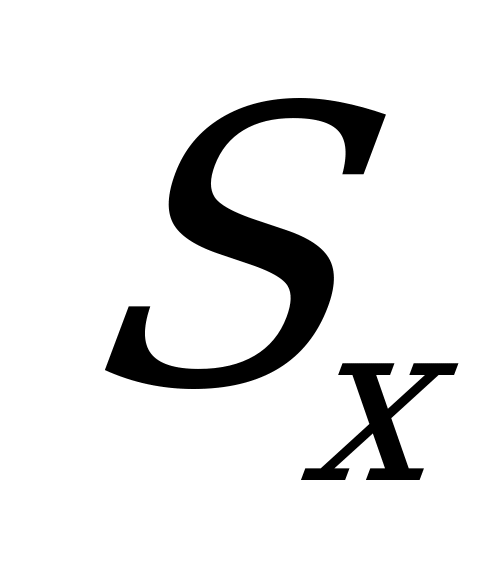 и
и  относительно осей х и у можно представить так:
относительно осей х и у можно представить так:
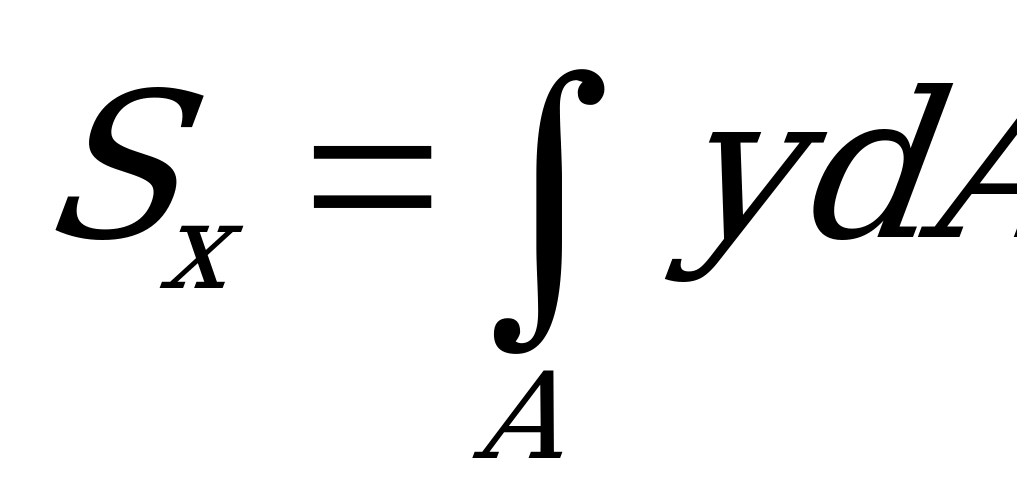 и
и 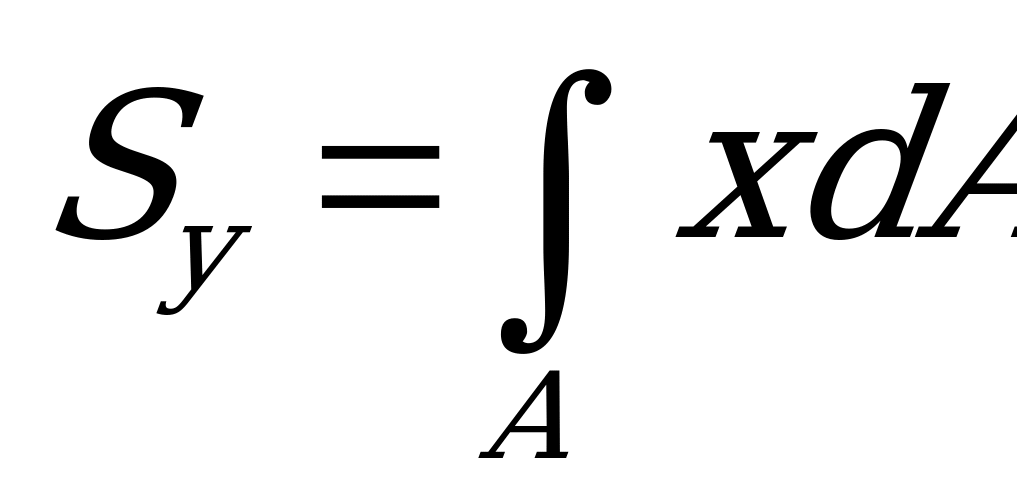 . (2.58)
. (2.58)
Из формул статики следует:
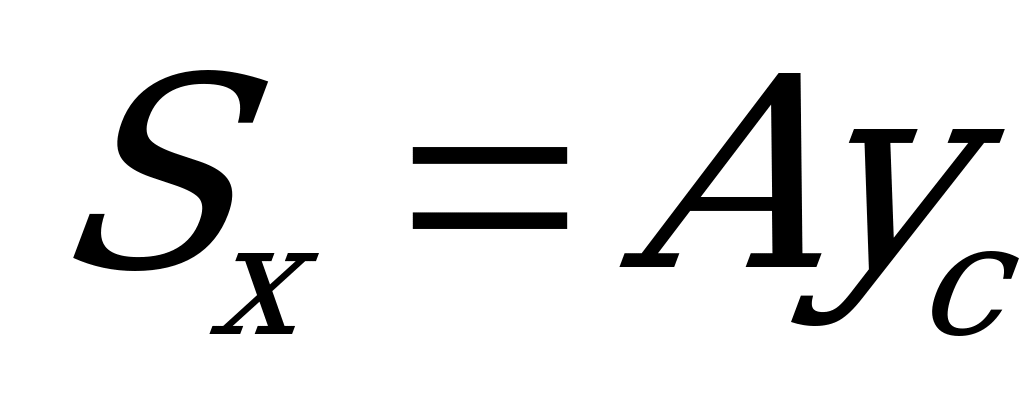 и
и 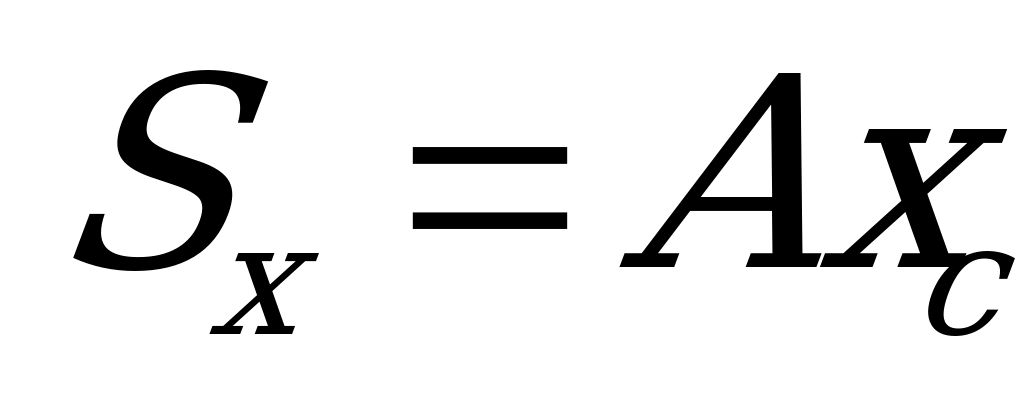 , (2.59)
, (2.59)
где  - площадь сечения;
- площадь сечения; 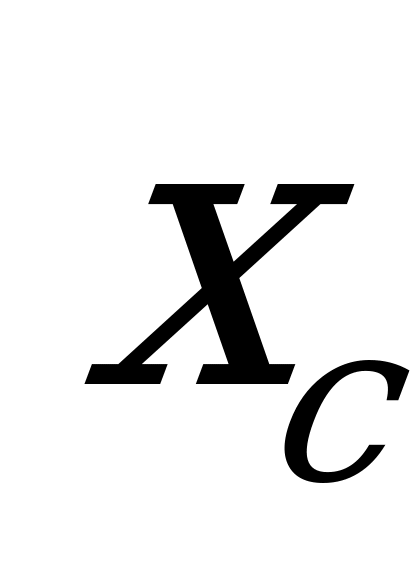 и
и 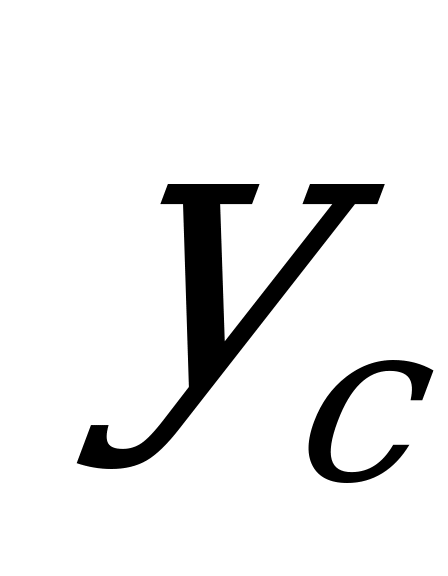 - координаты центра тяжести сечения. Легко заметить, что при
- координаты центра тяжести сечения. Легко заметить, что при 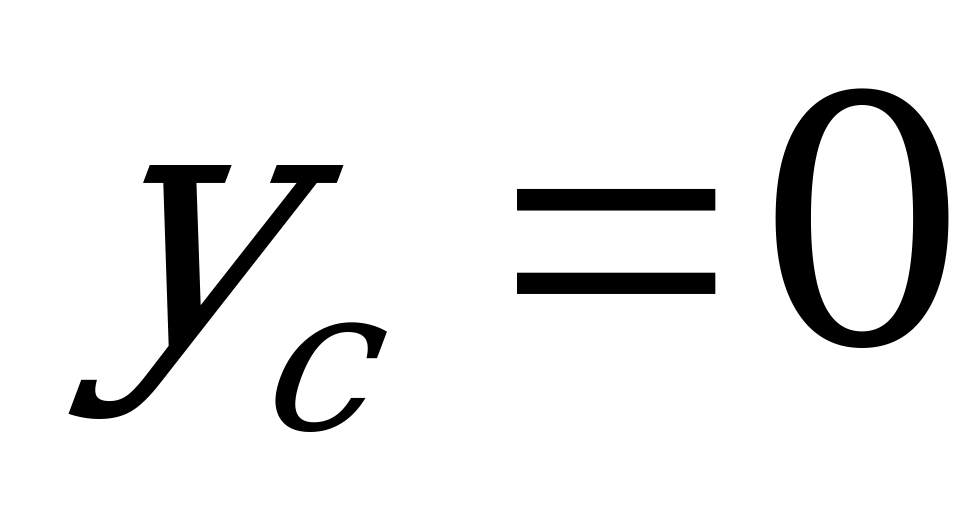 , когда ось х проходит через центр тяжести сечения,
, когда ось х проходит через центр тяжести сечения, 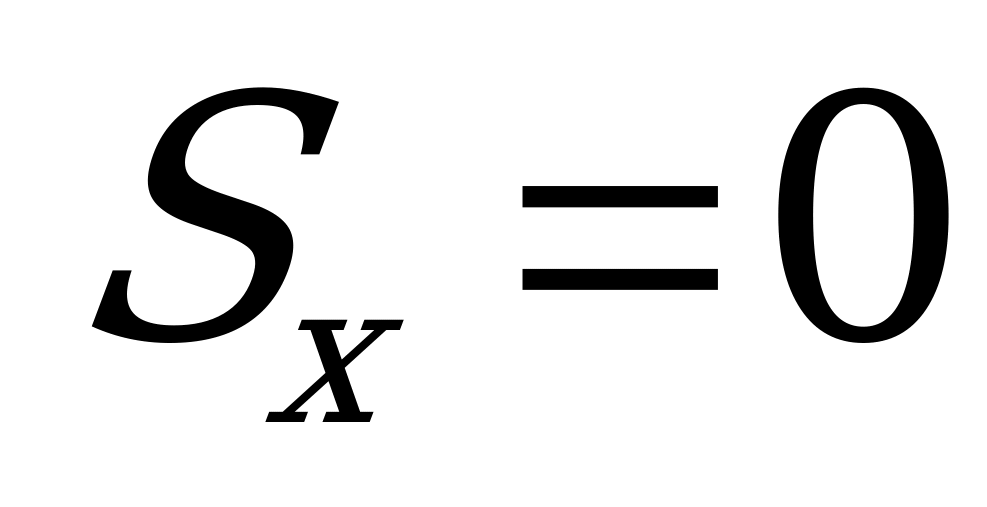 : статические моменты сечения относительно центральных осей равны нулю.
: статические моменты сечения относительно центральных осей равны нулю.
При исследовании зависимости между крутящим моментом и касательными напряжениями возникла еще одна геометрическая характеристика – полярный момент инерции сечения 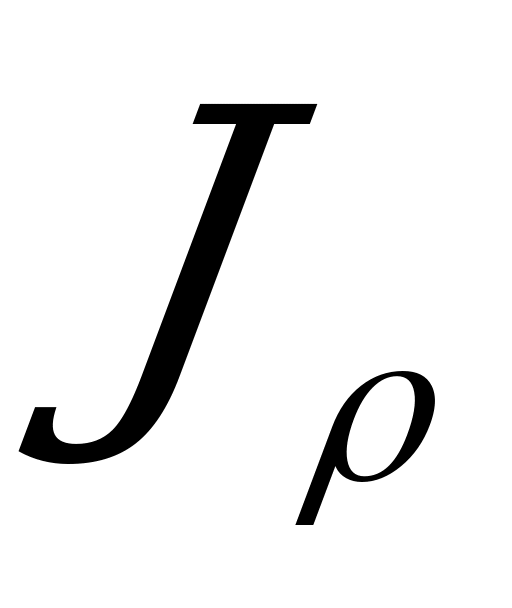 . Появление этой величины обусловлено неравномерностью распределения касательных напряжений по сечения при кручении.
. Появление этой величины обусловлено неравномерностью распределения касательных напряжений по сечения при кручении.
Познакомимся с новыми геометрическими характеристиками сечения - осевыми и центробежными моментами инерции относительно координатных осей (2.51).

 y
y
dA
х




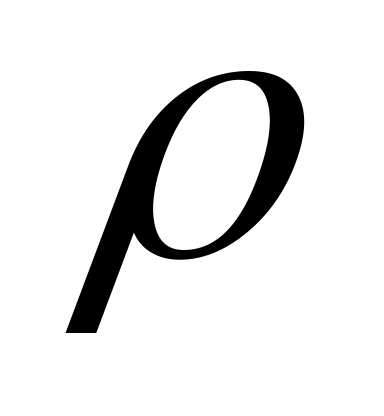
у

0 x 2.51
Представим себе, что сечение разделено на множество элементарных площадок  ( на 2.51 изображена одна из них), координаты которых х и у. Тогда интегралы
( на 2.51 изображена одна из них), координаты которых х и у. Тогда интегралы
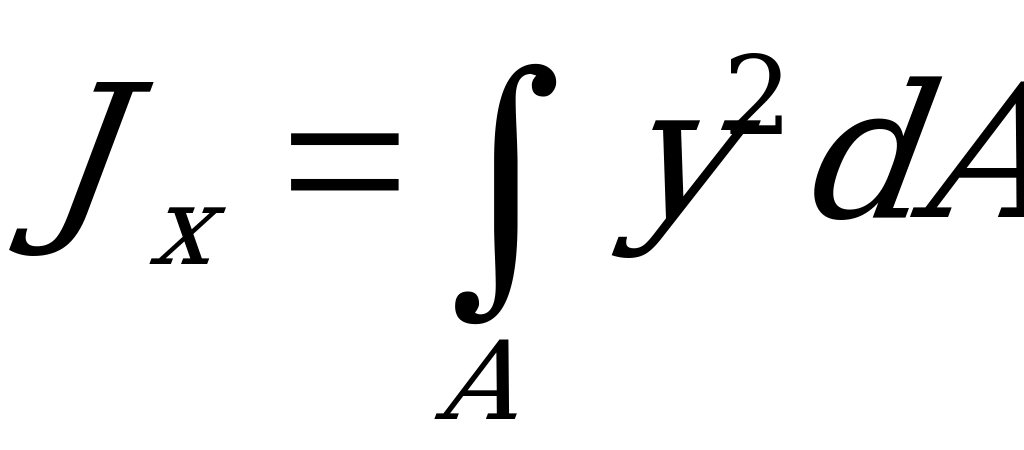 и
и 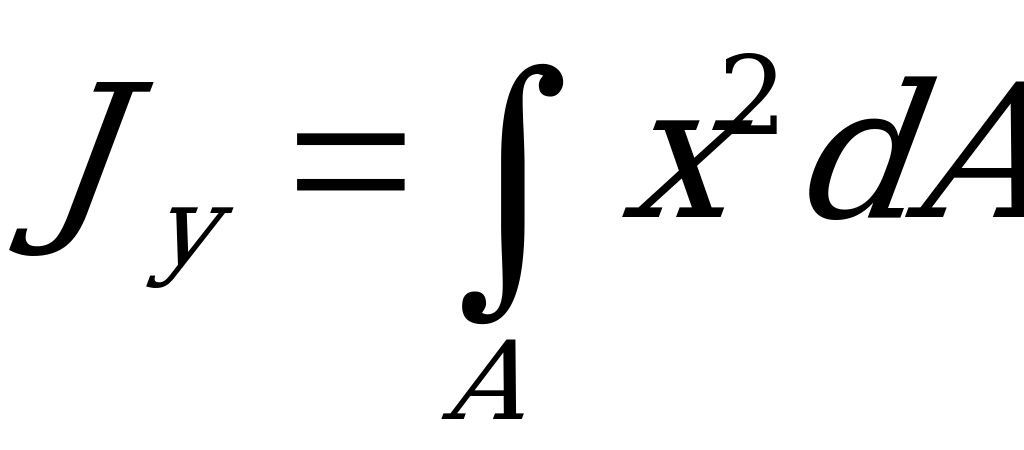 . (2.60)
. (2.60)
называются моментами инерции сечения относительно осей х и у, а интеграл
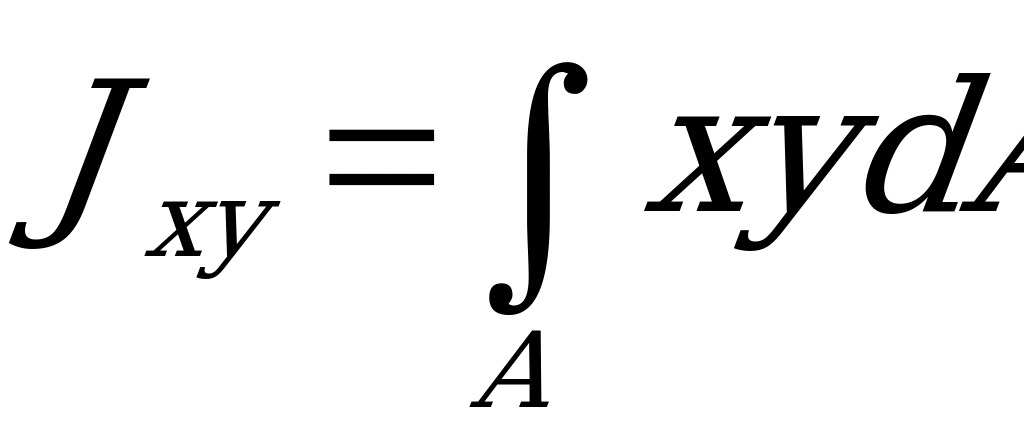 (2.61)
(2.61)
принято считать центробежным моментом инерции сечения относительно осей х и у.
Так же как и полярный момент инерции, осевые и центробежные моменты инерции выражаются в м4, см4 или мм4.
Значение площадки  положительно, поэтому независимо от знака координаты х или у осевые моменты инерции всегда положительны, а центробежный момент инерции может быть как положительным, так и отрицательным в зависимости от расположения сечения относительно осей х и у.
положительно, поэтому независимо от знака координаты х или у осевые моменты инерции всегда положительны, а центробежный момент инерции может быть как положительным, так и отрицательным в зависимости от расположения сечения относительно осей х и у.
Расстояние 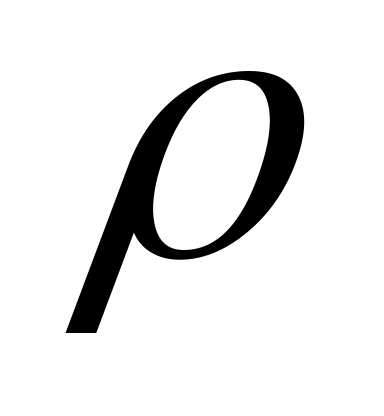 между элементарной площадкой
между элементарной площадкой  и началом координат связано с координатами площадки очевидной зависимостью (2.51)
и началом координат связано с координатами площадки очевидной зависимостью (2.51)
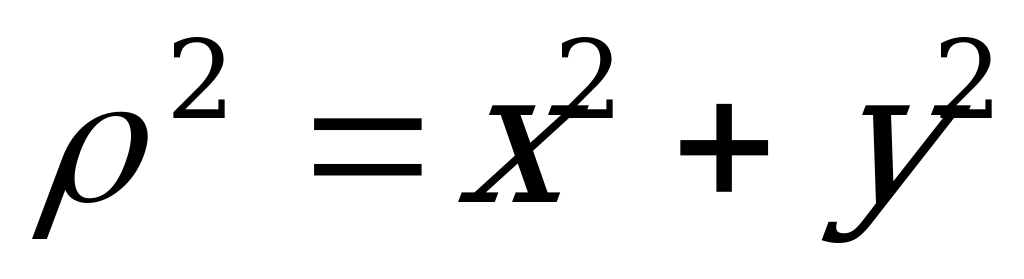 .
.
Умножив на  обе части этого равенства, а затем проинтегрировав их по всей площади сечения:
обе части этого равенства, а затем проинтегрировав их по всей площади сечения:
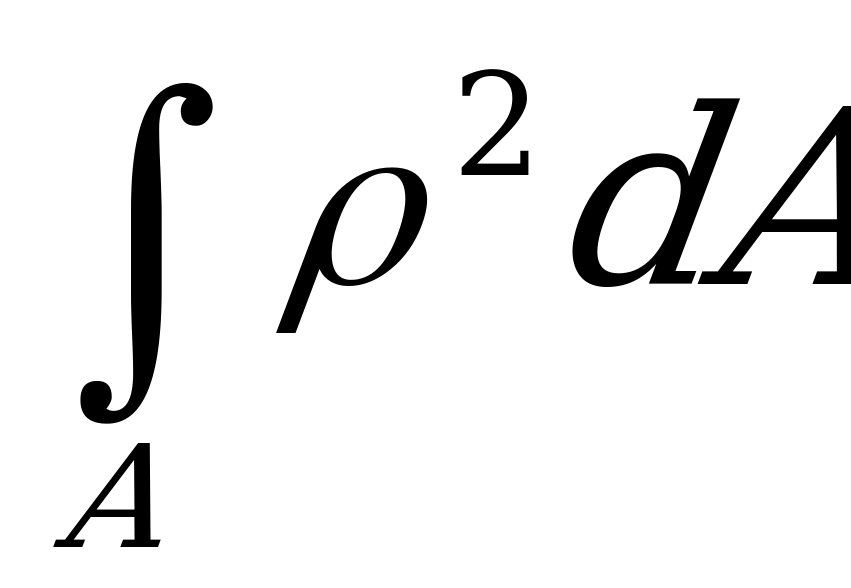
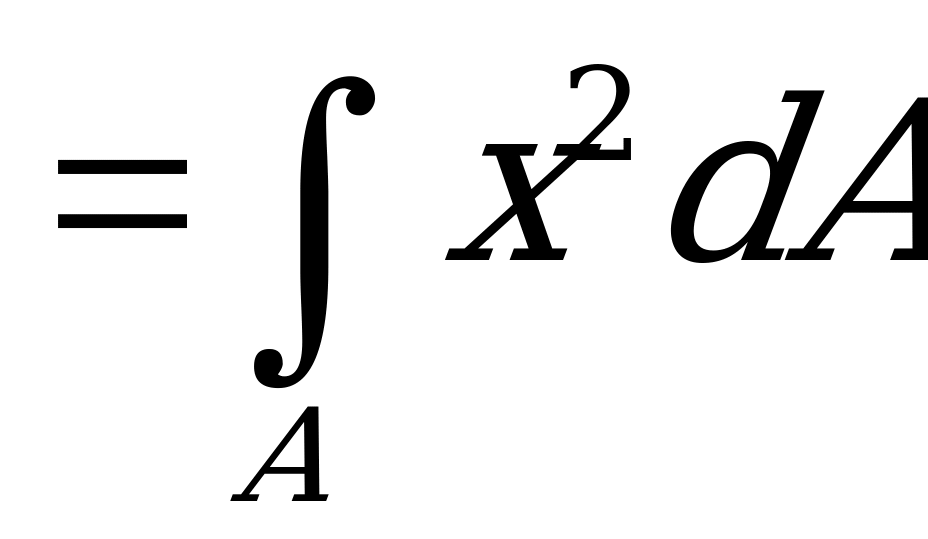 +
+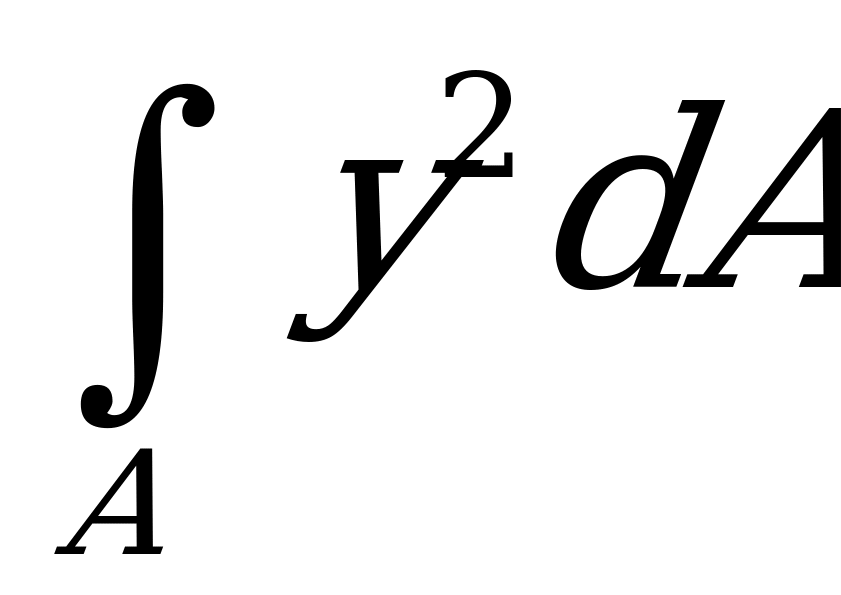 ,
,
получим важную зависимость между осевыми и полярными моментами инерции

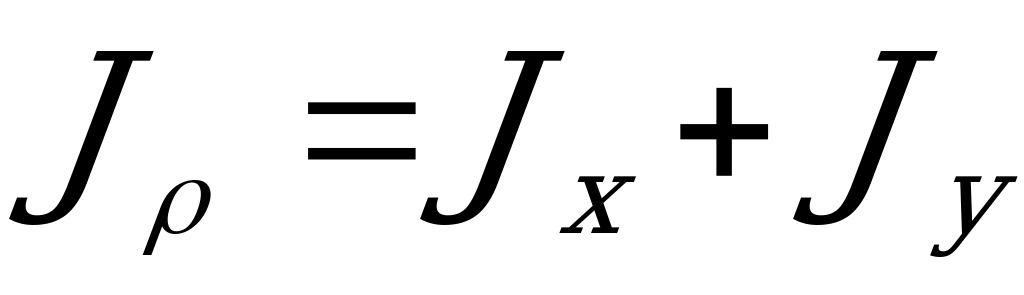 . (2.62)
. (2.62)
Сумма осевых моментов инерции сечения относительно взаимно перпендикулярных осей равна полярному моменту инерции относительно точки пересечения этих осей. Моменты инерции относительно осей, проходящих через центр тяжести сечения, называются центральными.
Между моментами инерции сечения относительно параллельных осей, из которых одна центральная, существует важная зависимость, используемая далее в расчетах. Расположим сечение в осях координат 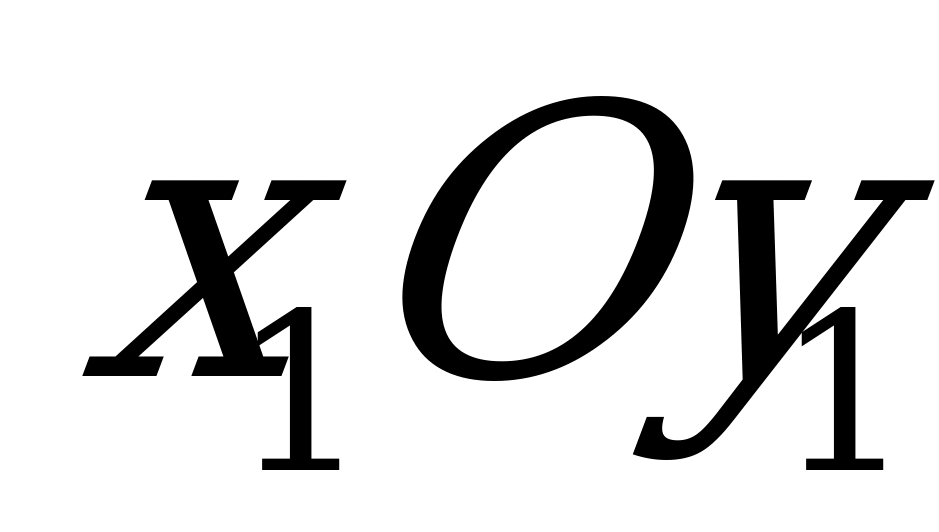 , а затем через центр тяжести С сечения проведем оси Сх║Ох1 и Су║Оу1 (2.52). Координаты элементарной площадки
, а затем через центр тяжести С сечения проведем оси Сх║Ох1 и Су║Оу1 (2.52). Координаты элементарной площадки  сечения в осях
сечения в осях 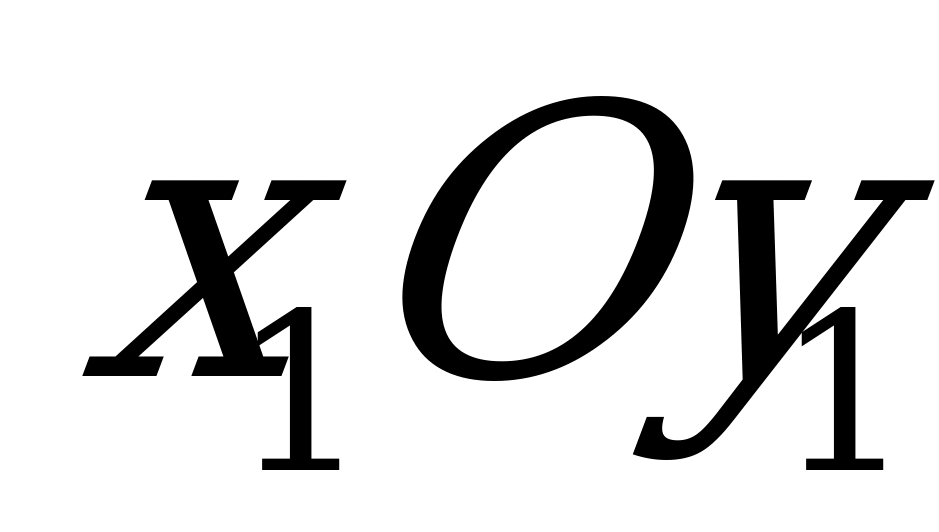 связаны с координатами в центральных осях равенствами
связаны с координатами в центральных осях равенствами
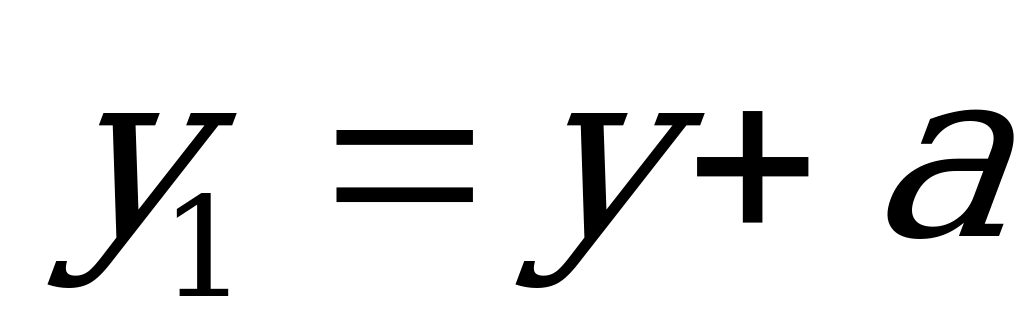 и
и 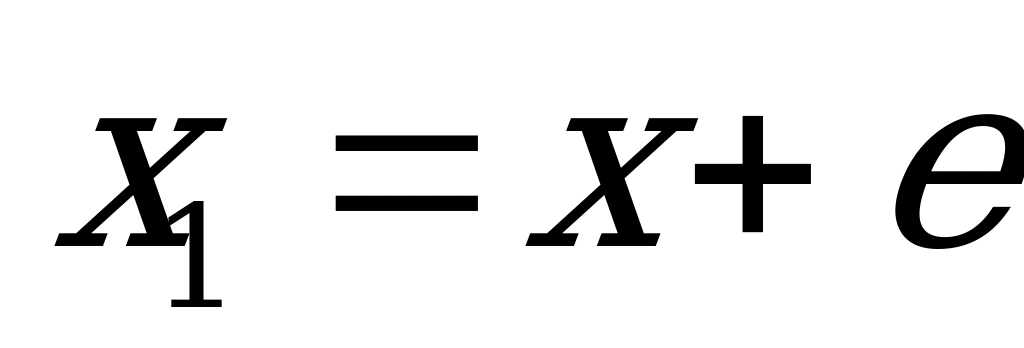 ,
,
где а и е – расстояния между осями.
Возведем обе части первого равенства во вторую степень:
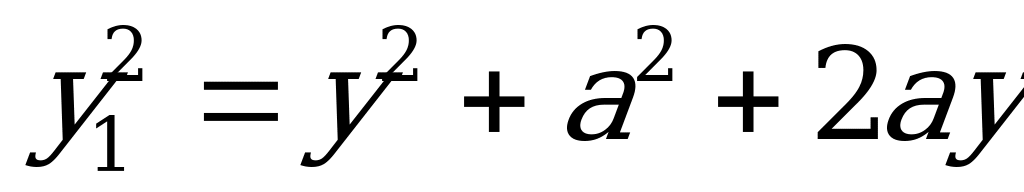 .
.
Умножим обе части этого равенства на  и проинтегрируем по всей площади сечения:
и проинтегрируем по всей площади сечения:

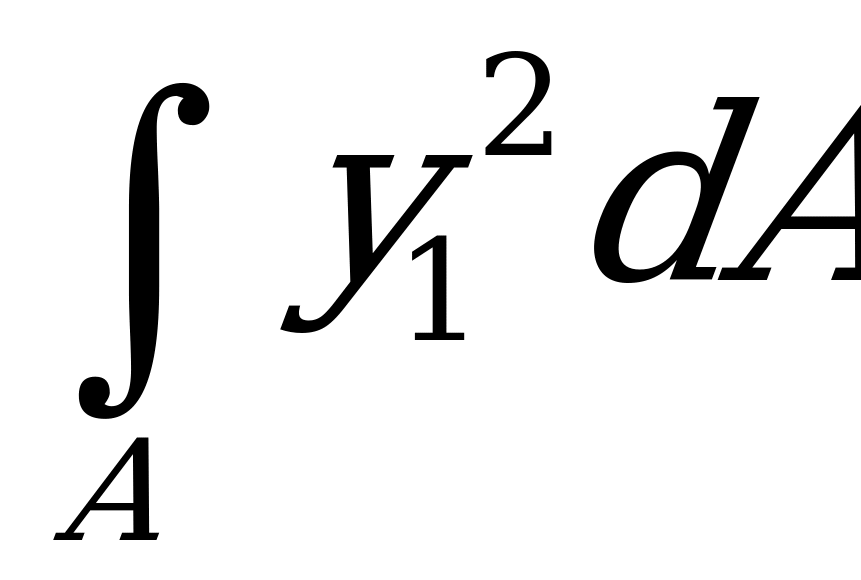
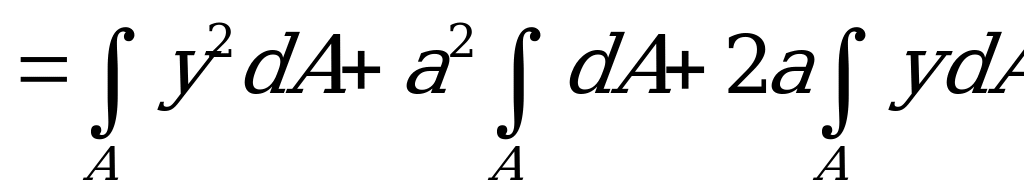 .
.
 у
у


 y1 х1
y1 х1
 х
х

 е1
е1 

у

 С х
С х
а у1

0 x1
2.52
Рассматривая каждый интеграл по отдельности, видим: 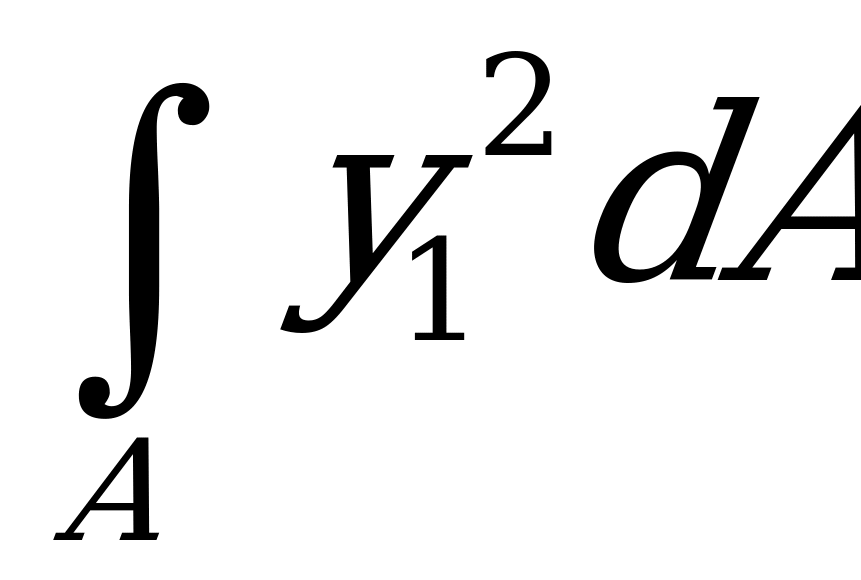 =
=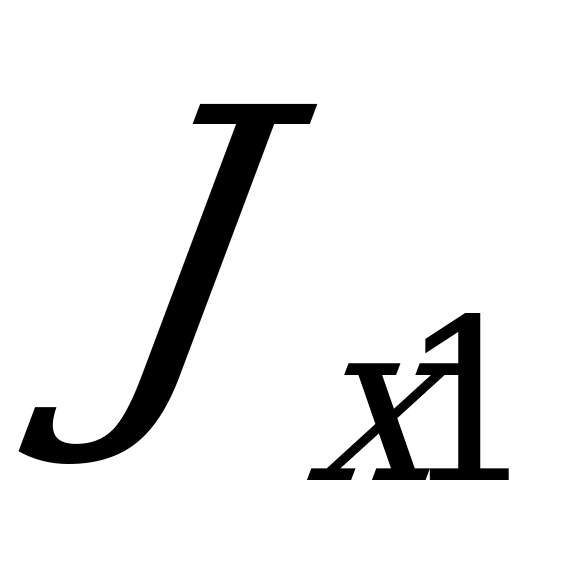 - момент инерции сечения относительно оси, параллельной центральной;
- момент инерции сечения относительно оси, параллельной центральной; 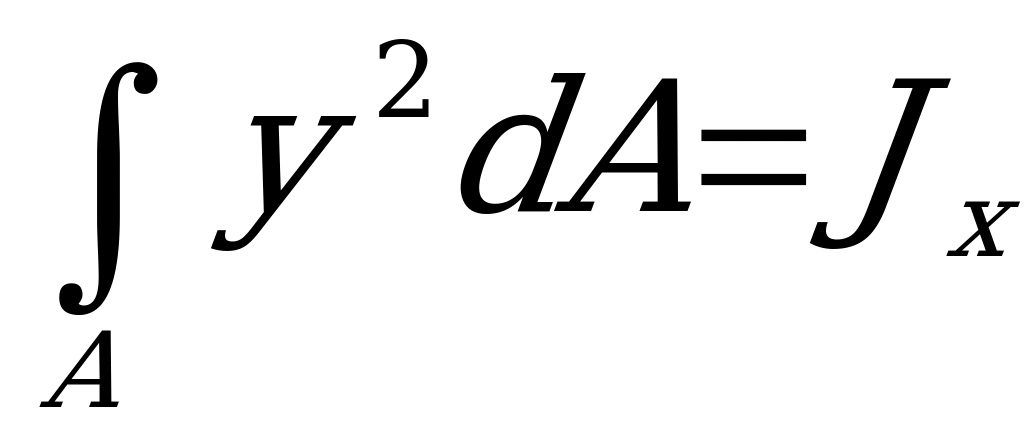 - центральный момент инерции сечения;
- центральный момент инерции сечения; 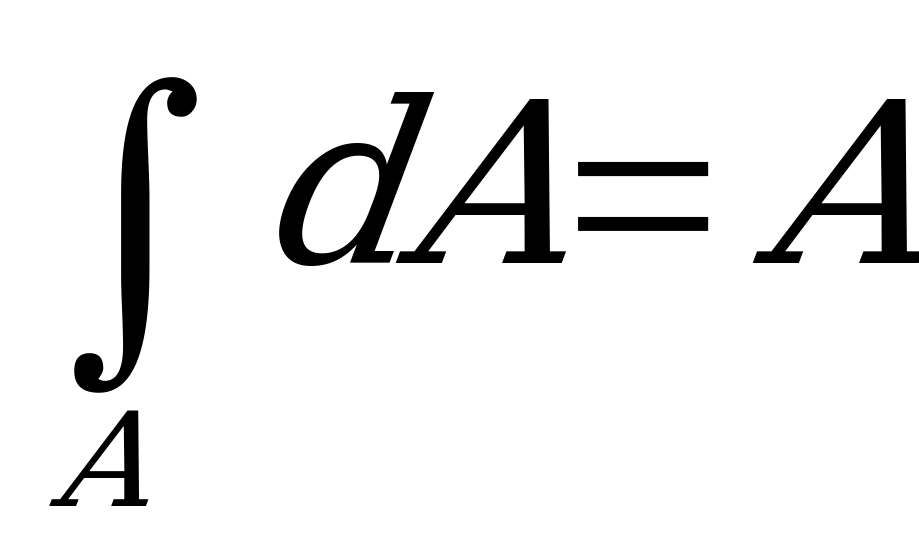 - площадь сечения;
- площадь сечения; 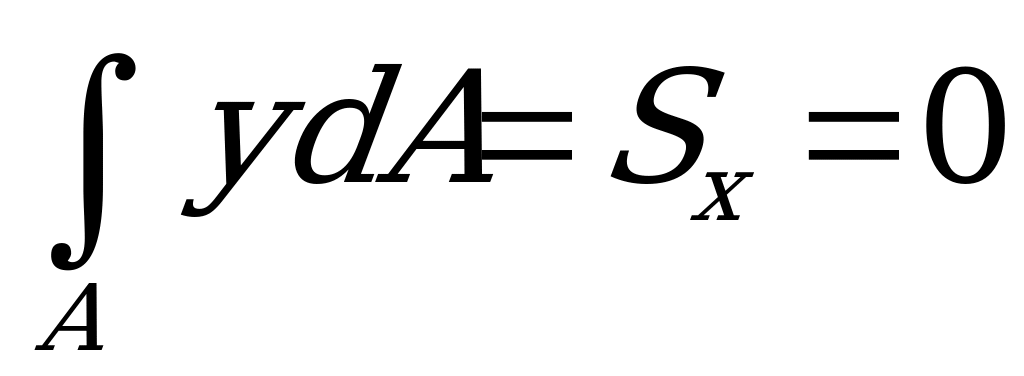 - статический момент сечения относительно центральной оси, как известно, равен нулю.
- статический момент сечения относительно центральной оси, как известно, равен нулю.
Следовательно, в окончательном виде последнее равенство запишется так:
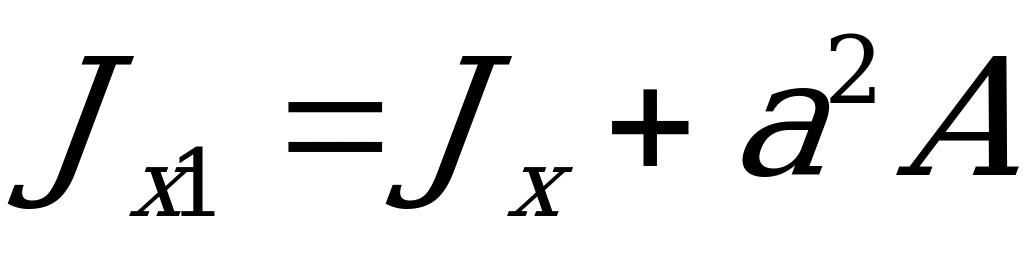 . (2.63)
. (2.63)
Аналогично, из равенства 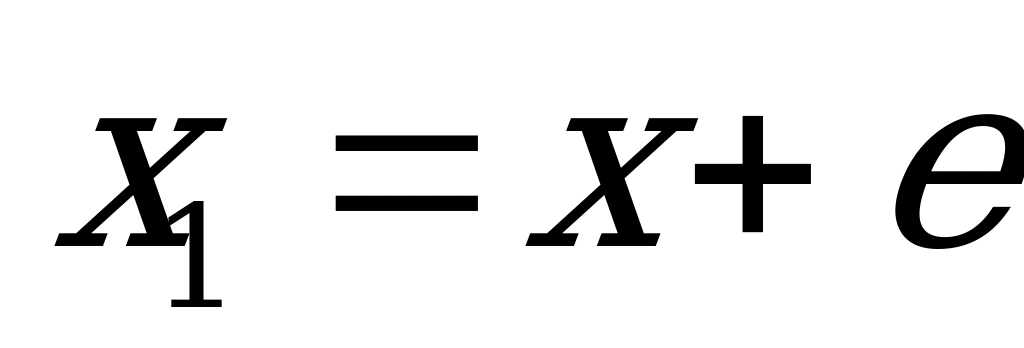 получим
получим
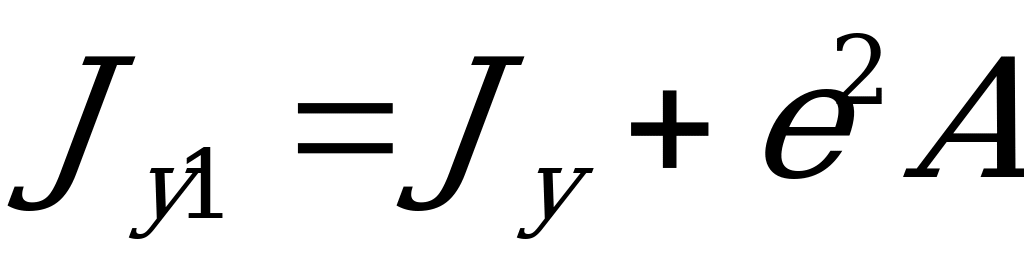 . (2.64)
. (2.64)
Таким образом, момент инерции сечения относительно оси, параллельной центральной, всегда больше центрального момента инерции на произведение квадрата расстояния между осями на площадь сечения.
Интеграл Мора.
Допустим, что для бруса, нагруженного силой 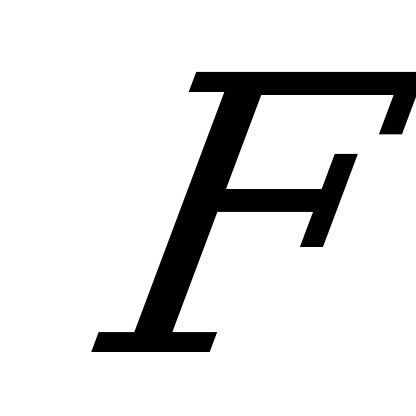 (2.89), требуется определить перемещение точки К в направлении у.
(2.89), требуется определить перемещение точки К в направлении у.
Проведем из точки 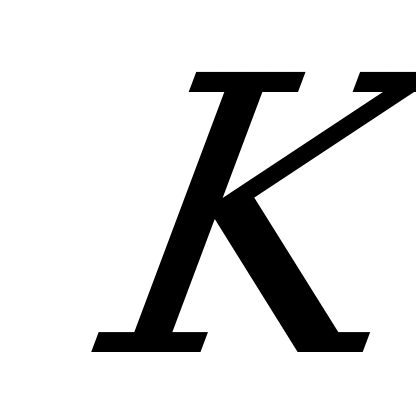 касательную к участку бруса слева в точке О и выделим у этой точки элемент длиной
касательную к участку бруса слева в точке О и выделим у этой точки элемент длиной 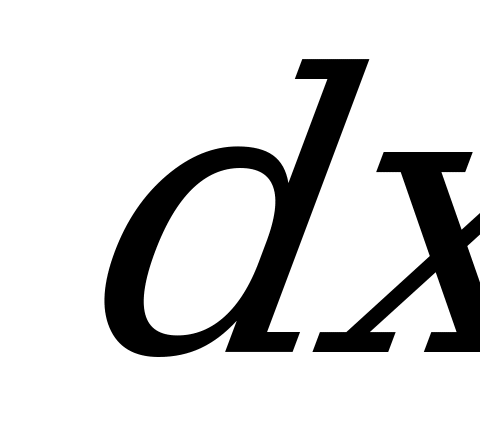 . При нагружении бруса внешней силой
. При нагружении бруса внешней силой 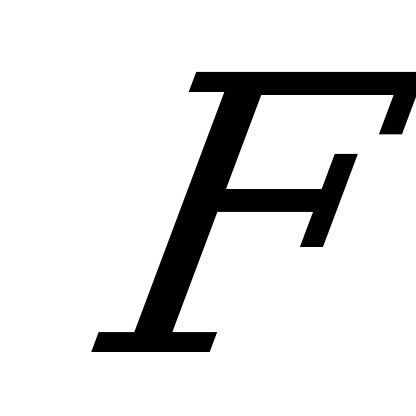 кривизна элемента
кривизна элемента 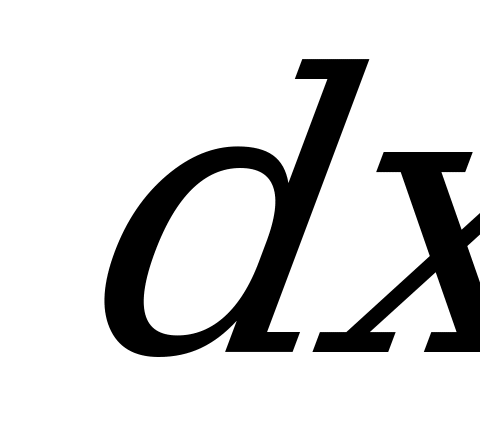 изменится на
изменится на 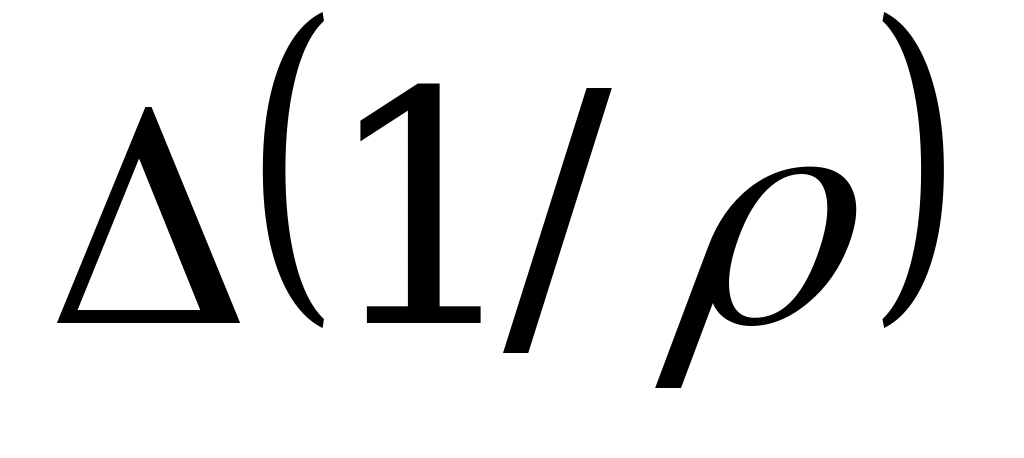 и правое его сечение повернется относительно левого на угол
и правое его сечение повернется относительно левого на угол 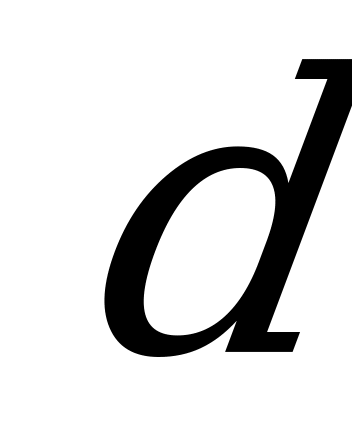 θ, значение которого, согласно формулам
θ, значение которого, согласно формулам 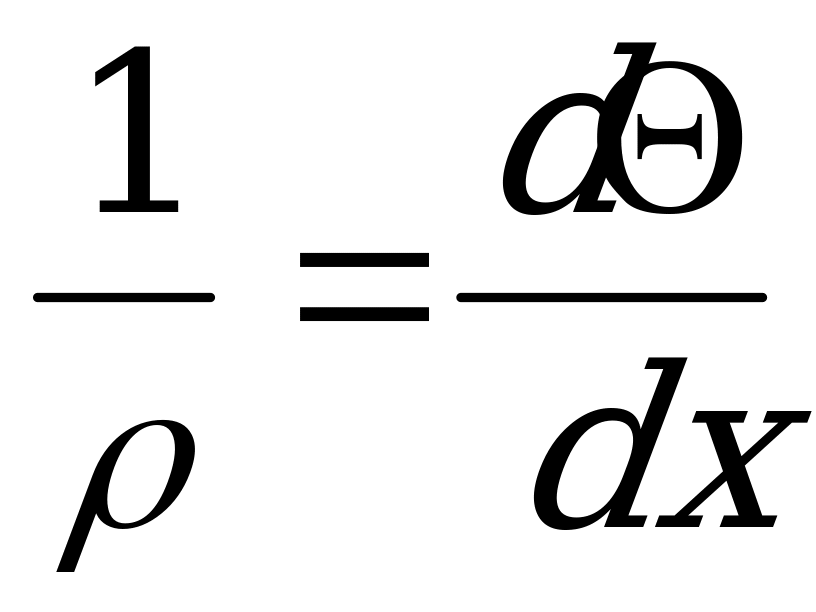 и
и 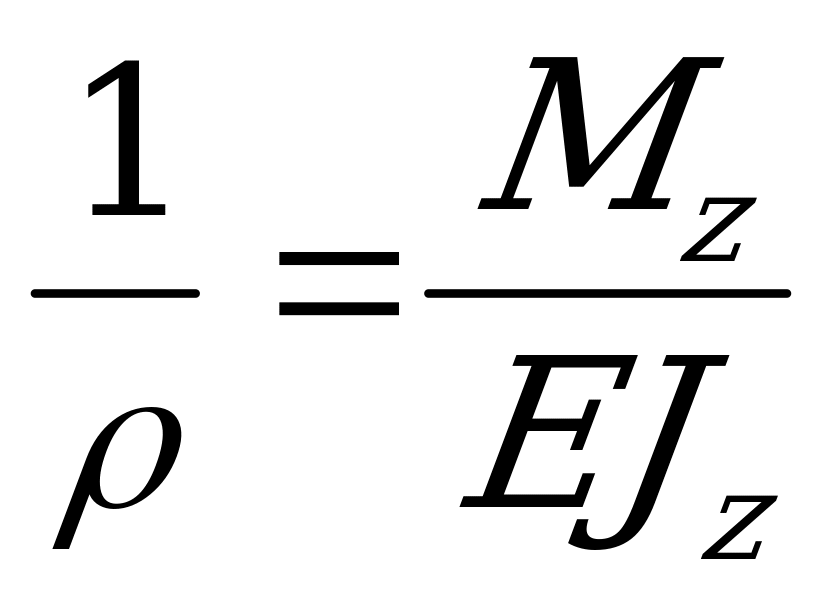 , запишем так:
, запишем так:
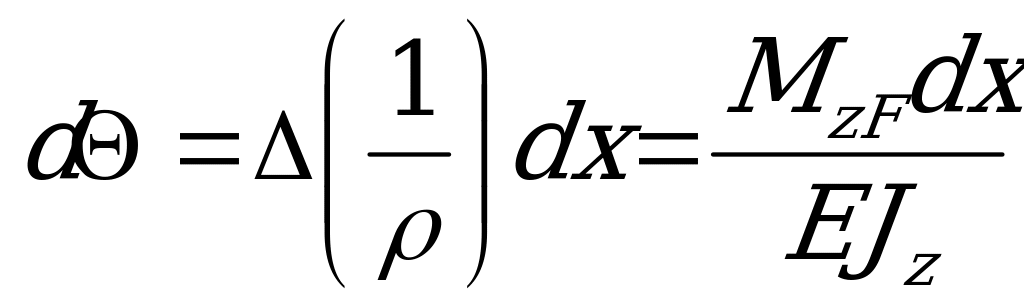 .
.
 y
y
C

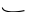
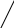
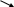 dx
dx
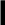







 B F
B F
 d θ K1
d θ K1



dθ
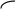

K1
2.89
Из-за этого поворота правая часть бруса повернется как жесткое целое на тот же угол dθ, а точка К по направлению у переместится на
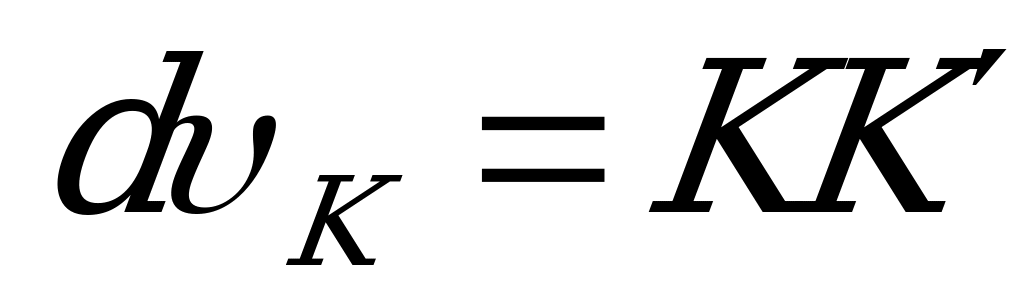 .
.
Из  , из
, из 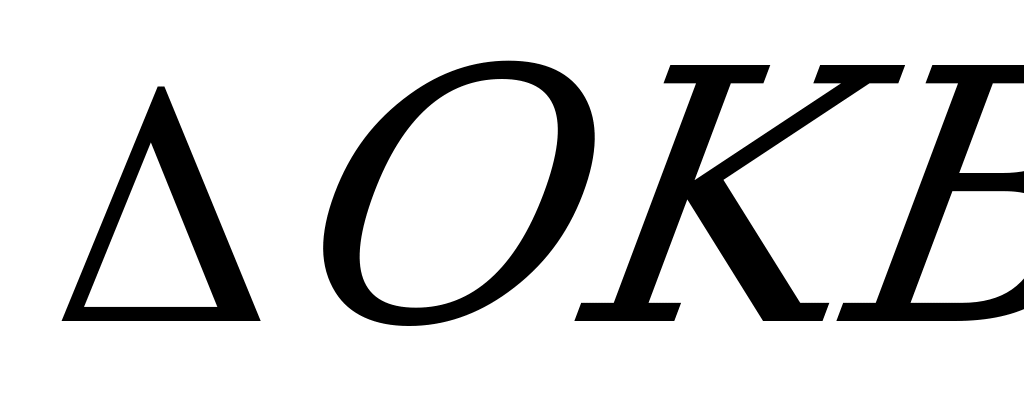 , пренебрегая длиной элемента
, пренебрегая длиной элемента 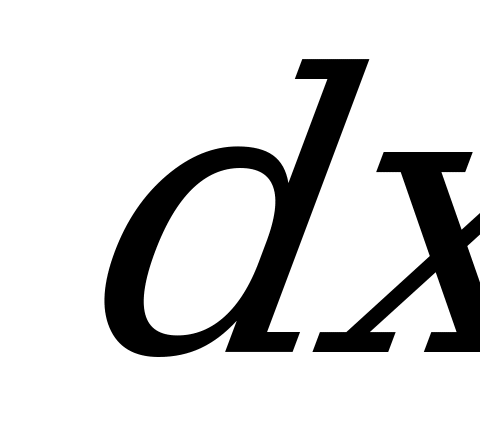 и считая
и считая 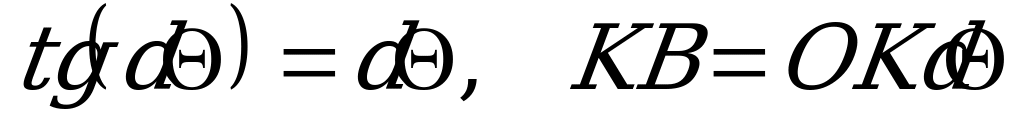 . Таким образом,
. Таким образом,
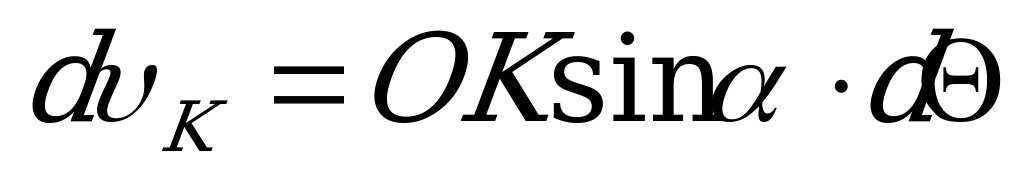 .
.
Из 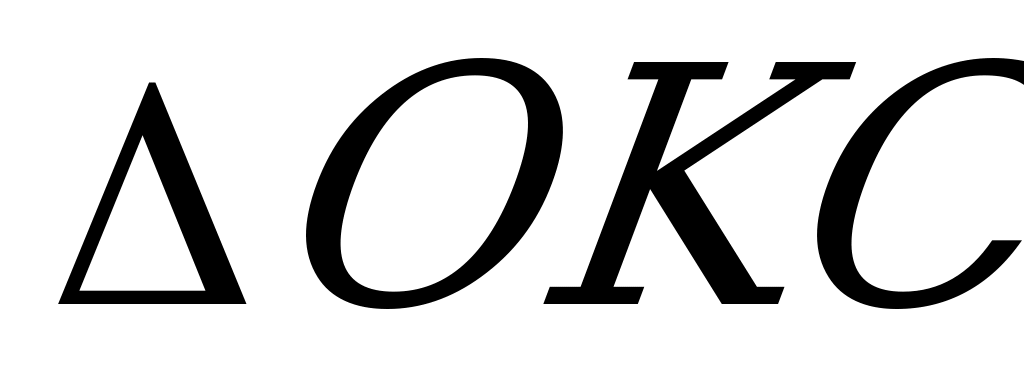 видим, что
видим, что 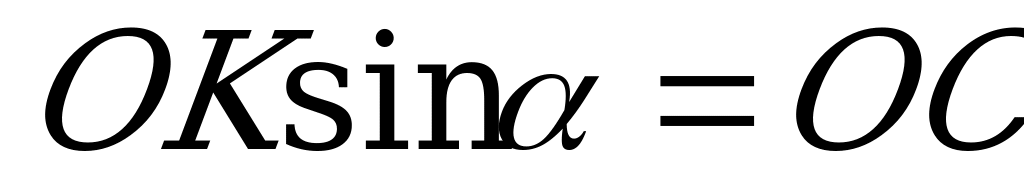 ; следовательно,
; следовательно,
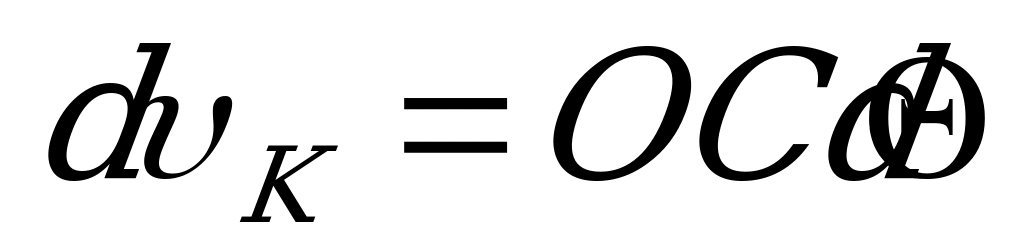 .
.
Если в точке К по направлению у приложить к брусу единичную (безразмерную) силу 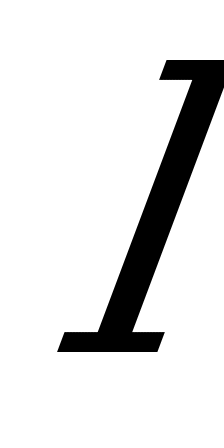 , то момент единичной силы
, то момент единичной силы 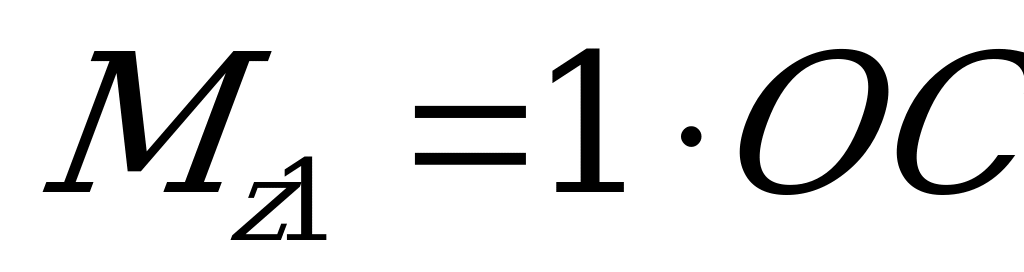 и тогда
и тогда 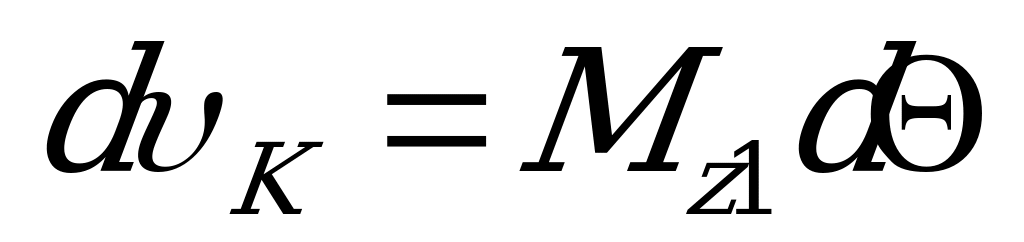 .
.
Подставив сюда полученное выше значение угла dθ, получим
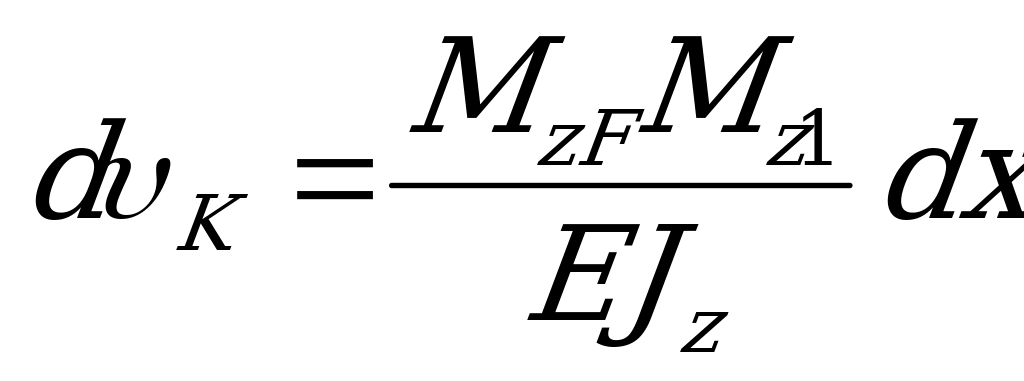 .
.
Интегрируя эти выражения отдельно для каждого участка 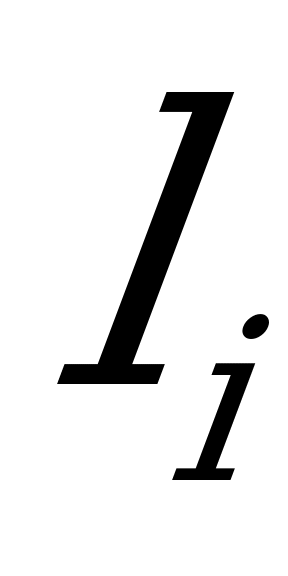 нагружения бруса и суммируя результаты, получим формулу интеграла Мора
нагружения бруса и суммируя результаты, получим формулу интеграла Мора
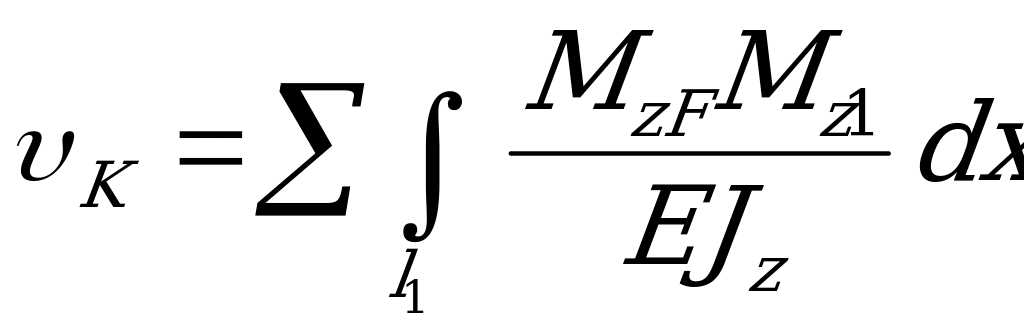 . (2.91)
. (2.91)
 а) F
а) F
K



l



б)
1
 K
K
 1
1

 в)
в)

 К 2.90
К 2.90
В случае, если жесткость сечения бруса по всей длине постоянна, формула 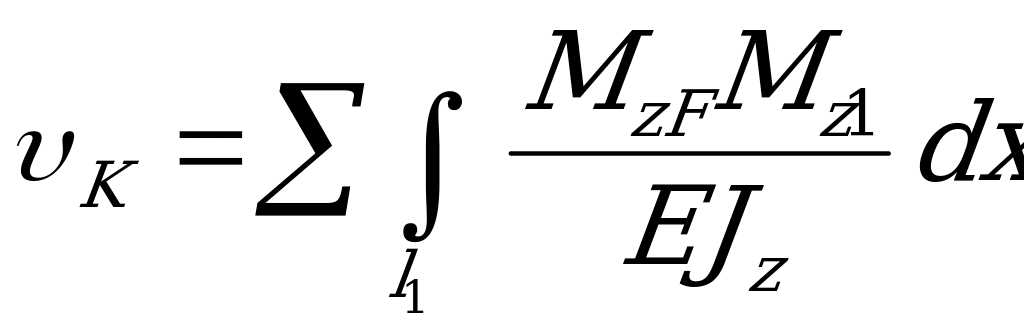 имеет вид
имеет вид
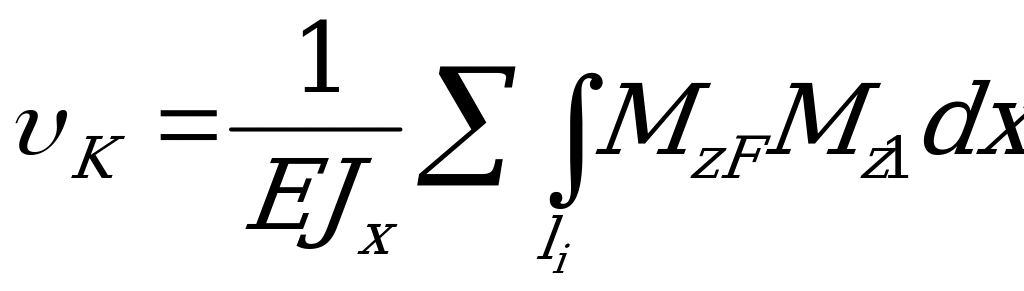 , (2.92)
, (2.92)
где 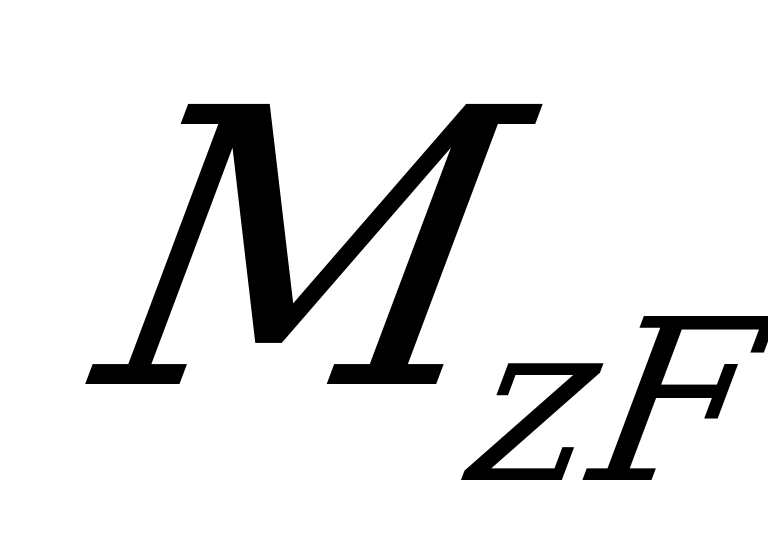 - уравнение избегающего момента от нагрузки
- уравнение избегающего момента от нагрузки 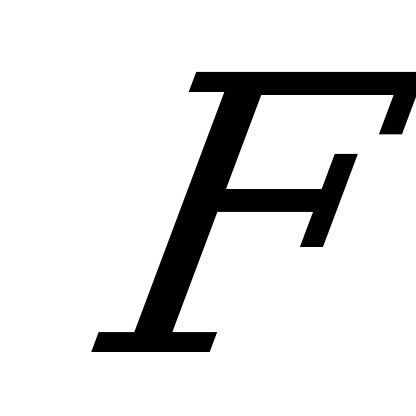 ;
; 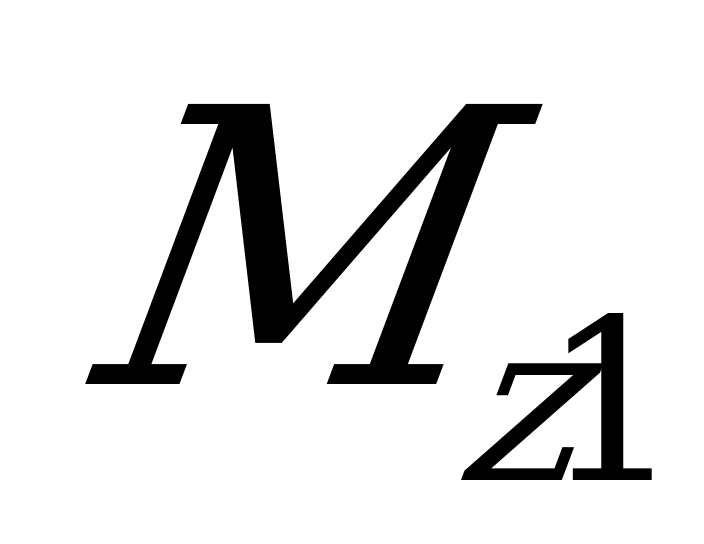 - уравнение изгибающего момента от единичной силы.
- уравнение изгибающего момента от единичной силы.
Для определения угла поворота сечения в точке К формула интеграла Мора аналогична формуле 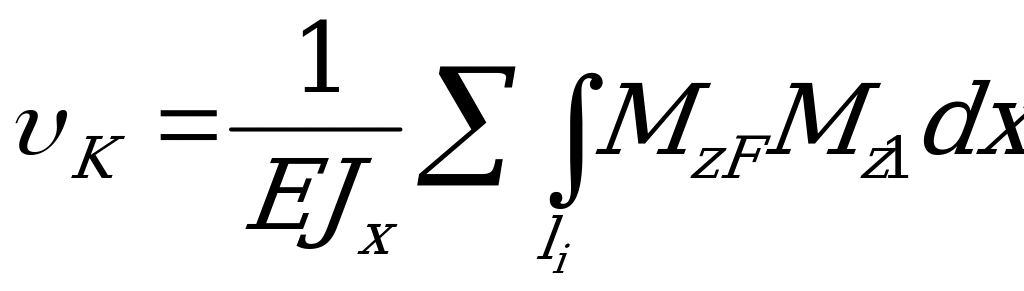 :
:
 θК =
θК =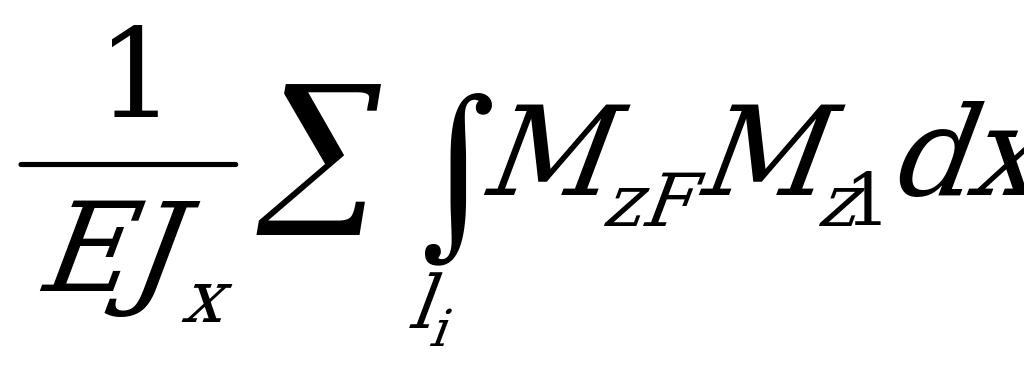 . (2.93)
. (2.93)
Только в этом случае 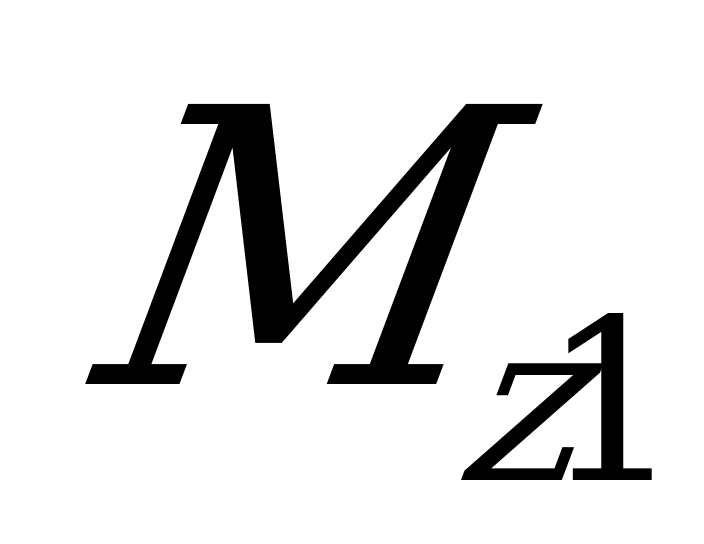 - уравнение изгибающего момента от единичного момента.
- уравнение изгибающего момента от единичного момента.
Пример 2.22. Определить прогиб 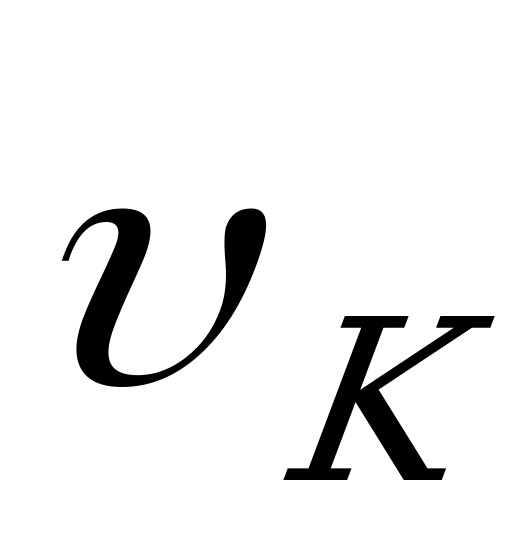 консоли (2.90, а) и угол поворота сечения в точке К.
консоли (2.90, а) и угол поворота сечения в точке К.
Решение. 1. Изгибающий момент от силы 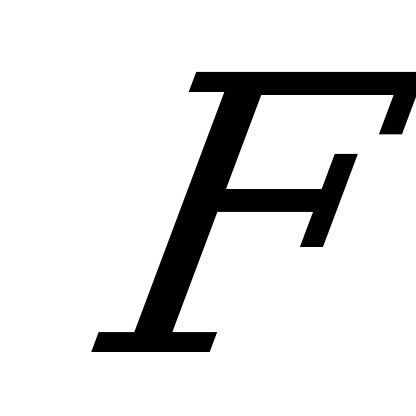 по всей длине консоли, т.е. при
по всей длине консоли, т.е. при 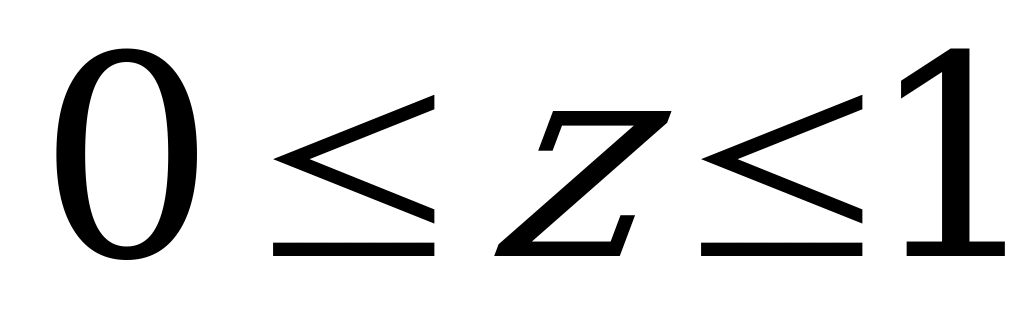 , имеет вид
, имеет вид

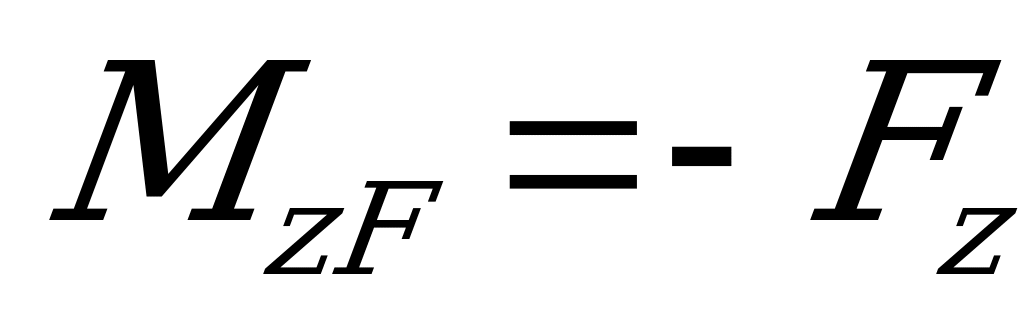 .
.
2. Сняв нагрузку 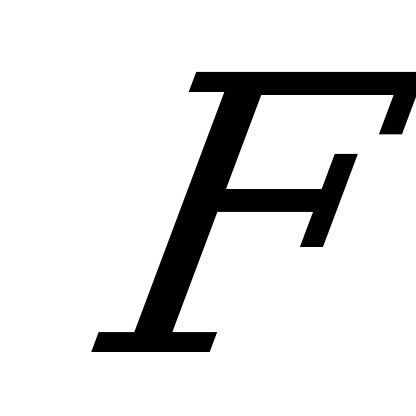 , приложим в точке К (в месте определения прогиба) единичную силу 1 (2.90,б). Уравнение изгибающего момента от единичной силы
, приложим в точке К (в месте определения прогиба) единичную силу 1 (2.90,б). Уравнение изгибающего момента от единичной силы 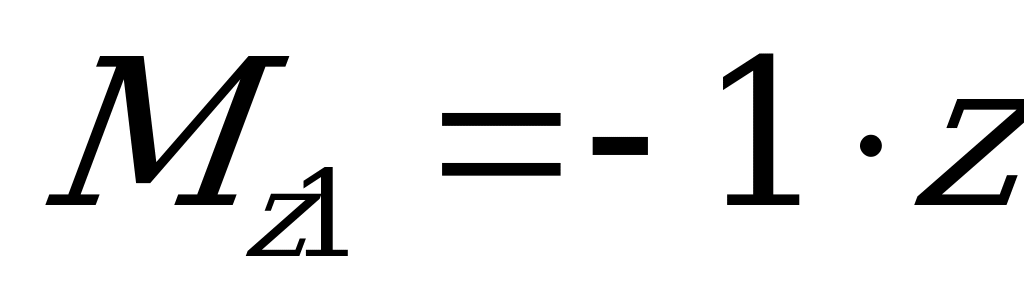 при
при 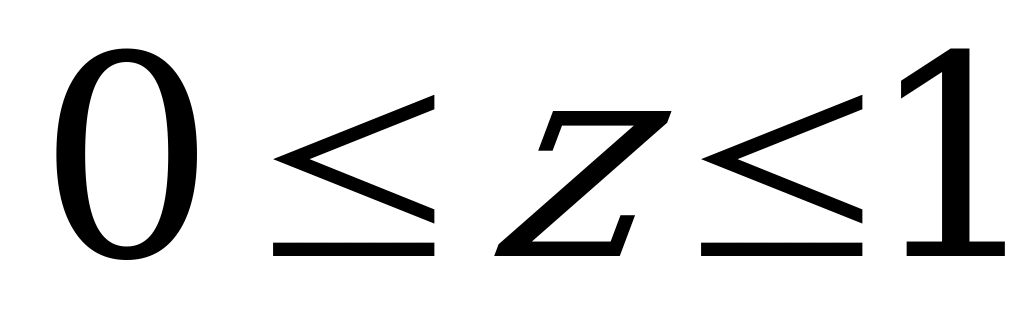 .
.
3. По формуле 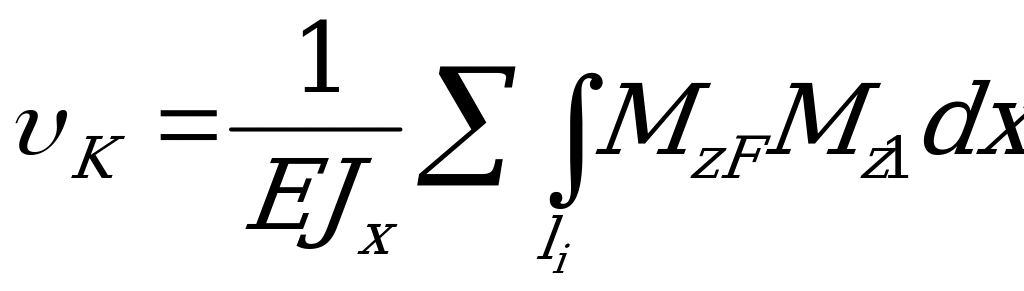
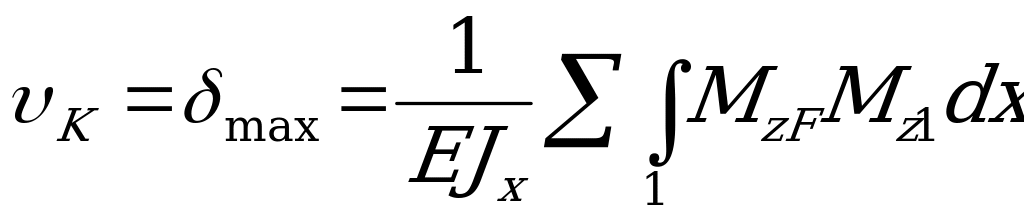 =
=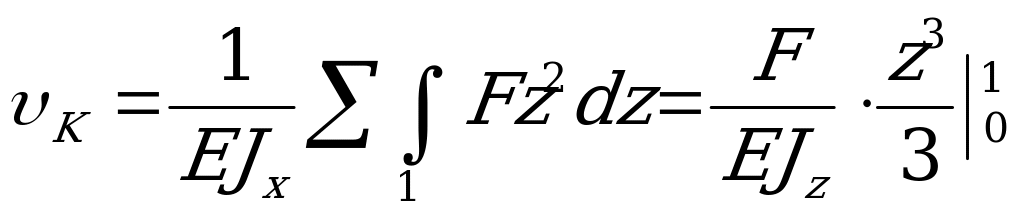 .
.
Подставляя значения 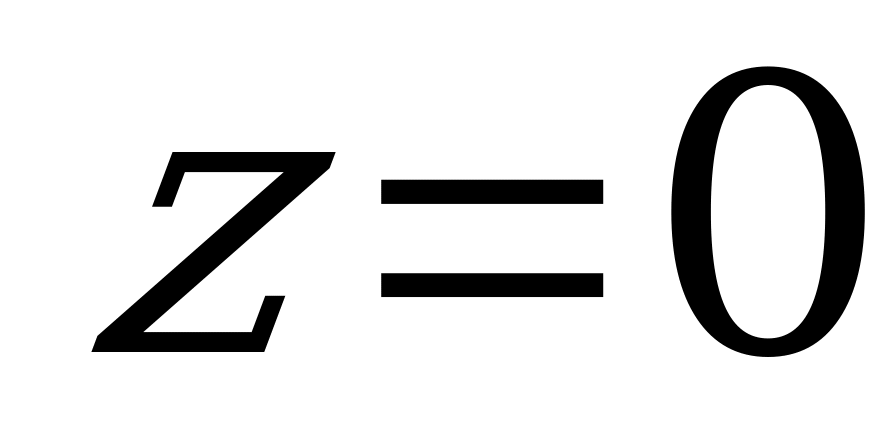 и
и 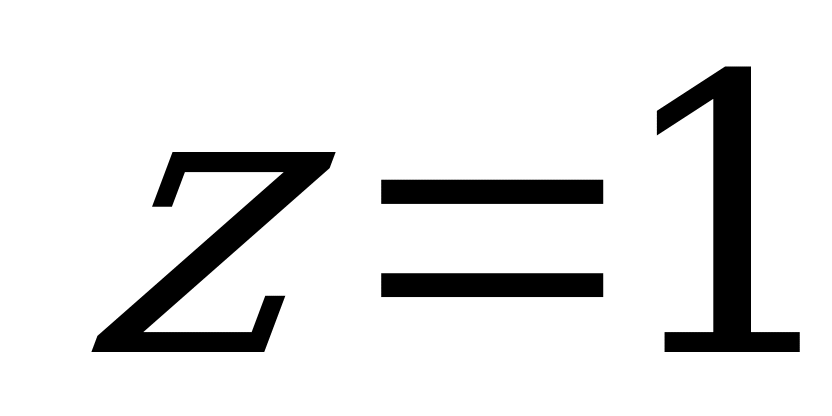 получим
получим
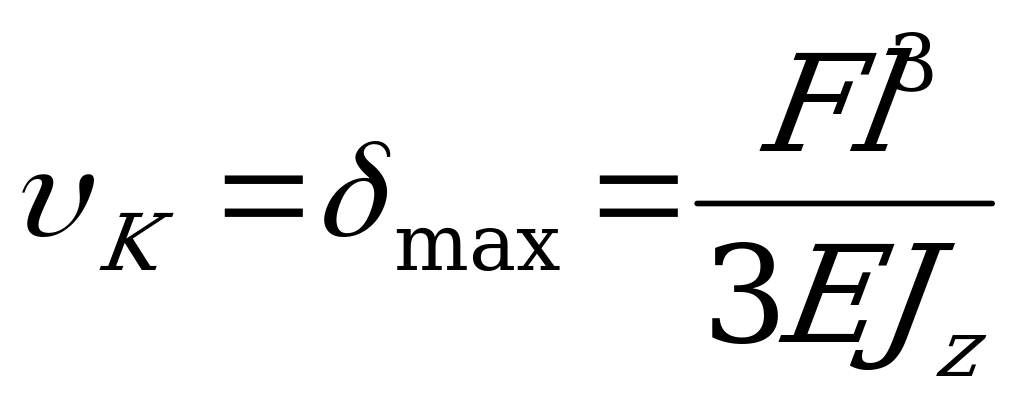 .
.
4. Для определения угла поворота, сняв нагрузку 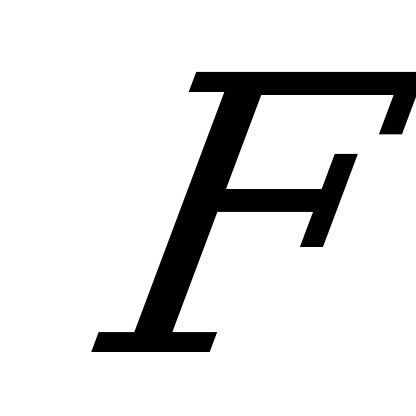 , приложим в точке К к балке единичный момент (2.90, в). Значение изгибающего момента по всей длине балки
, приложим в точке К к балке единичный момент (2.90, в). Значение изгибающего момента по всей длине балки
θ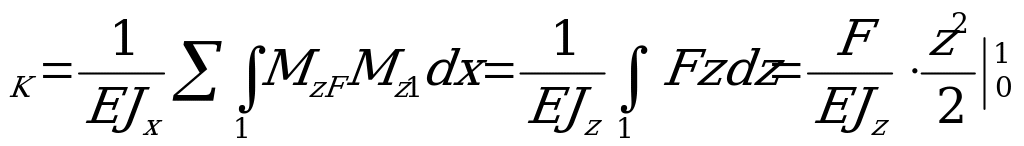
 .
.
или 
θК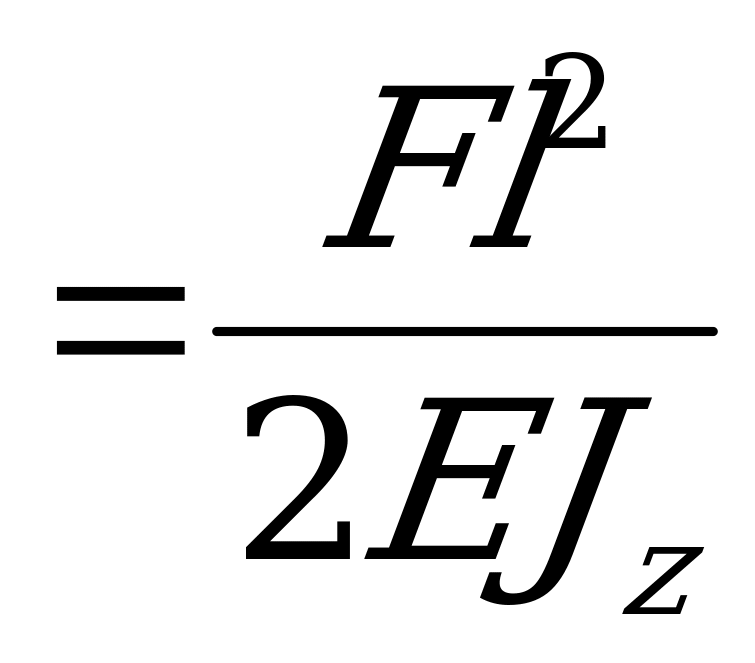 ..
..
Правило Верещагина.
Вычисление интеграла Мора целесообразно вести по правилу, предложенному А.Н. Верещагиным в 1925г. для прямолинейных брусьев.
Уравнение изгибающих моментов 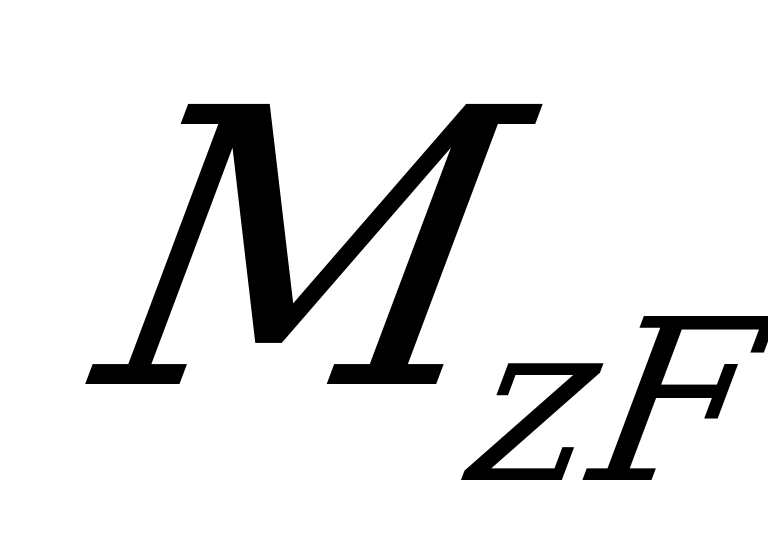 и
и 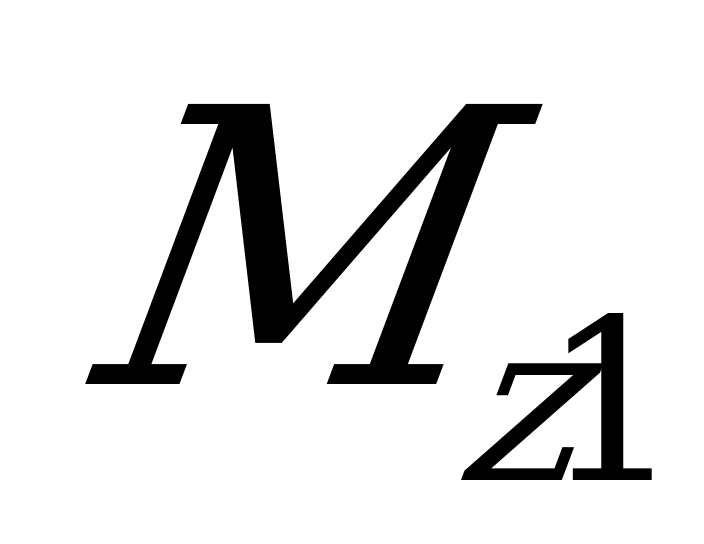 , входящих в формулу интеграла Мора, - это некоторые функции от х:
, входящих в формулу интеграла Мора, - это некоторые функции от х: 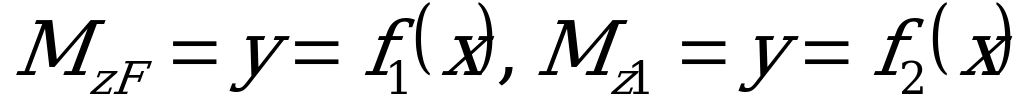 , а графики этих функций – эпюры
, а графики этих функций – эпюры 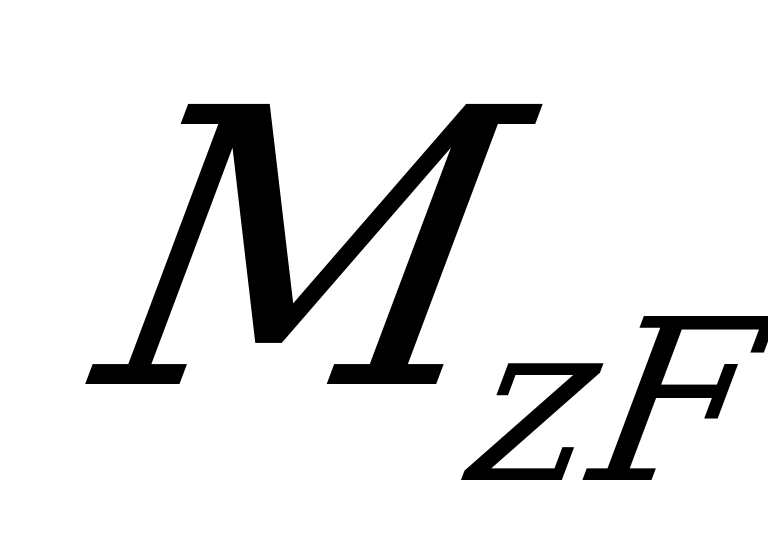 и
и 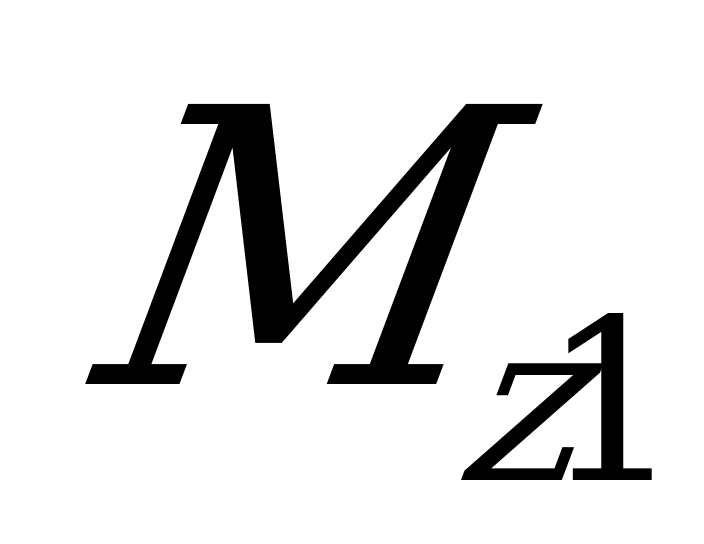 (2.91) на некотором участке балки. Причем если первая функция
(2.91) на некотором участке балки. Причем если первая функция 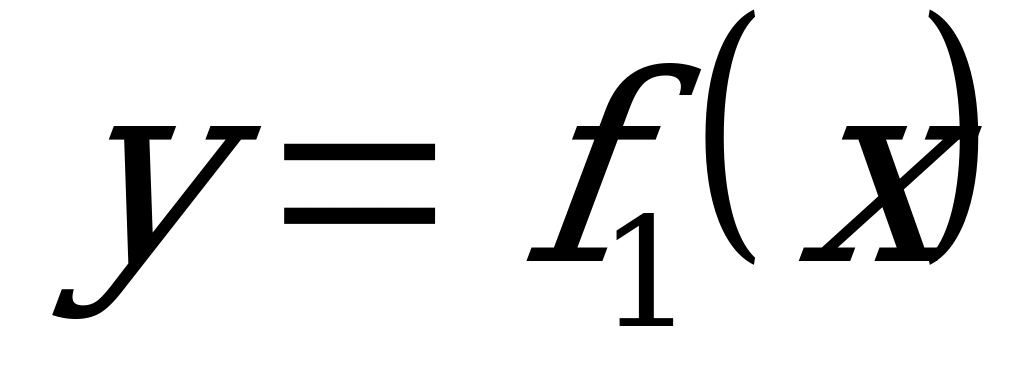 может быть и нелинейной, то вторая
может быть и нелинейной, то вторая 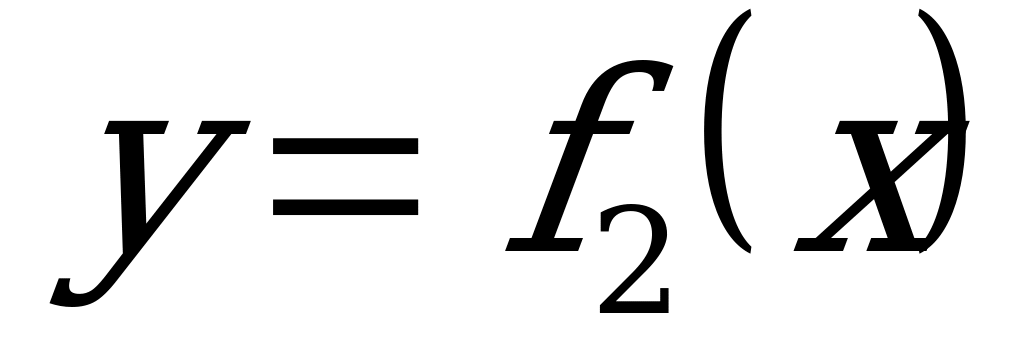 , выражающая изгибающий момент от единичной силы (или единичного момента), обязательно линейная. Поэтому ее можно представить уравнением прямой с угловым коэффициентом, т.е.
, выражающая изгибающий момент от единичной силы (или единичного момента), обязательно линейная. Поэтому ее можно представить уравнением прямой с угловым коэффициентом, т.е.
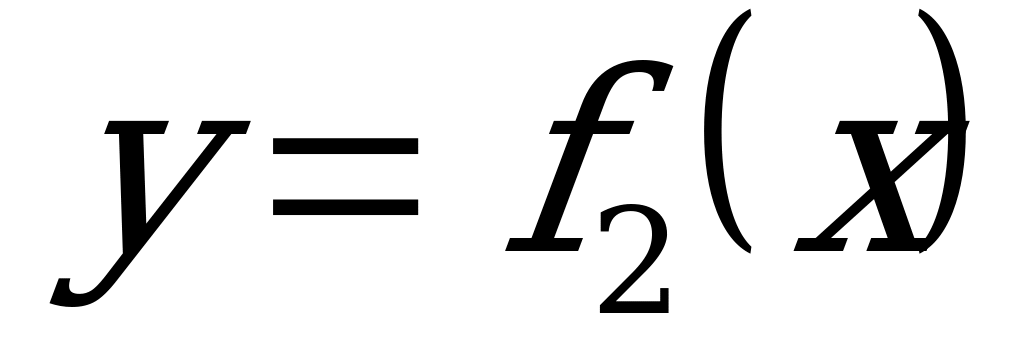
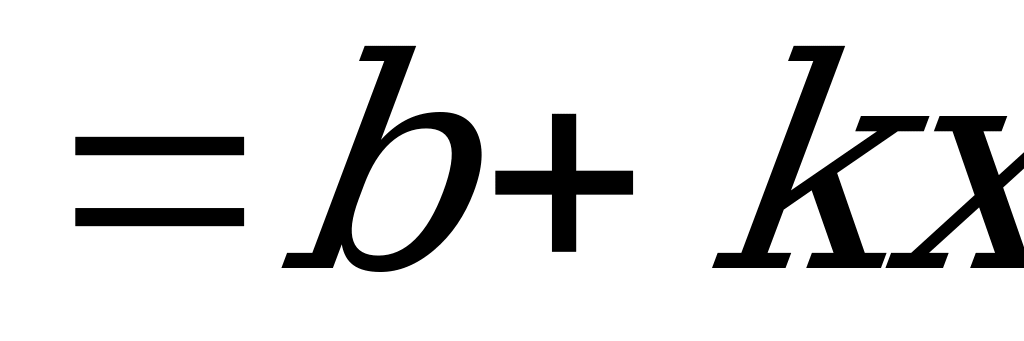 .
.
 Следовательно, вычисление интеграла
Следовательно, вычисление интеграла 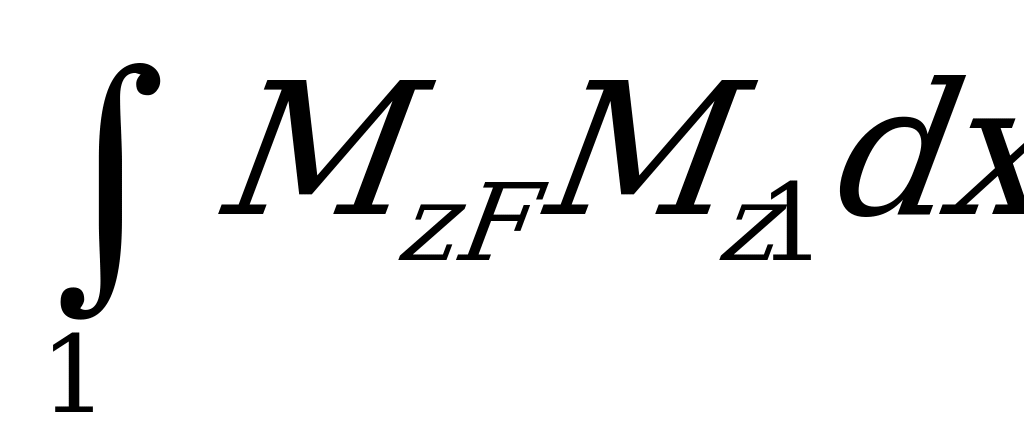 можно заменить вычислением интеграла
можно заменить вычислением интеграла
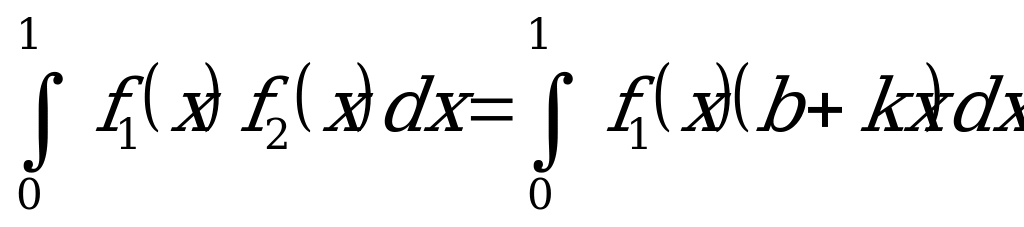 .
.
Раскрыв скобки под интегралом в правой части равенства, получим
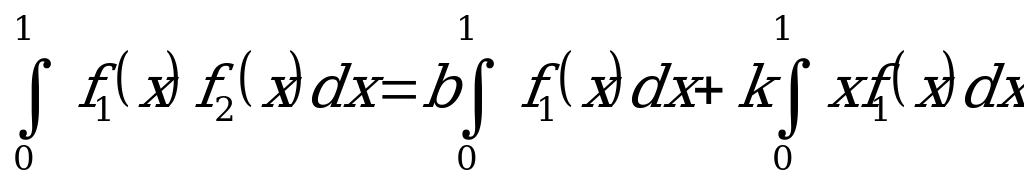 . (а)
. (а)
Произведение 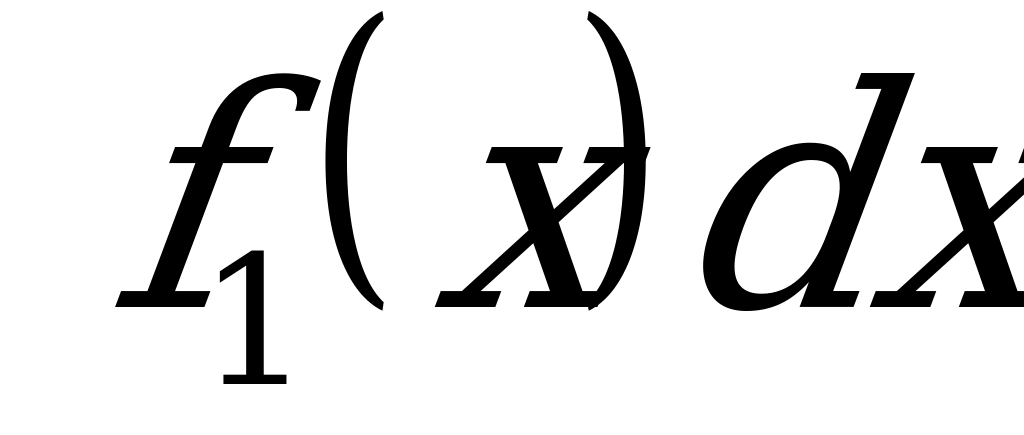 есть не что иное, как заштрихованная на рис. 2.91 элементарная площадка эпюры
есть не что иное, как заштрихованная на рис. 2.91 элементарная площадка эпюры 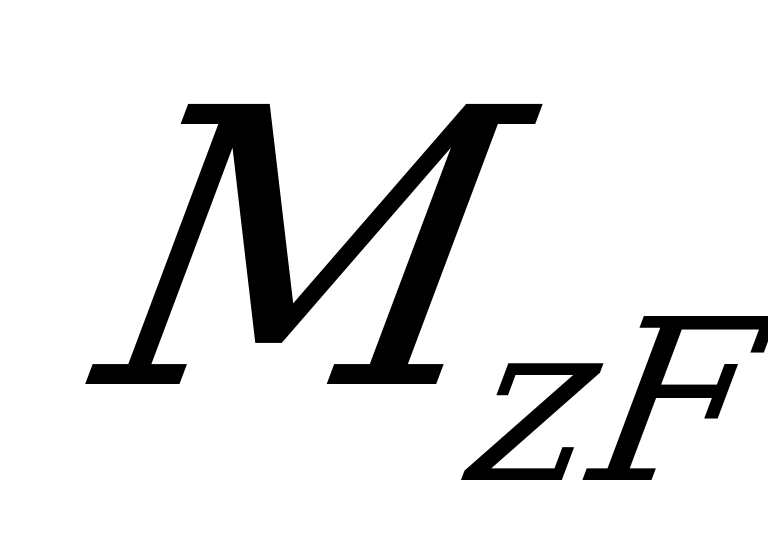 . Значит, первый интеграл в правой части равенства (а) выражает площадь эпюры
. Значит, первый интеграл в правой части равенства (а) выражает площадь эпюры 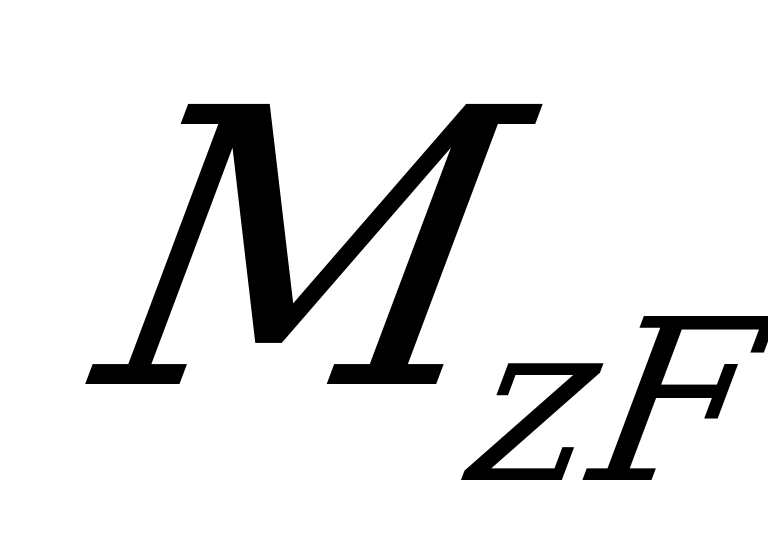 в интервале от
в интервале от 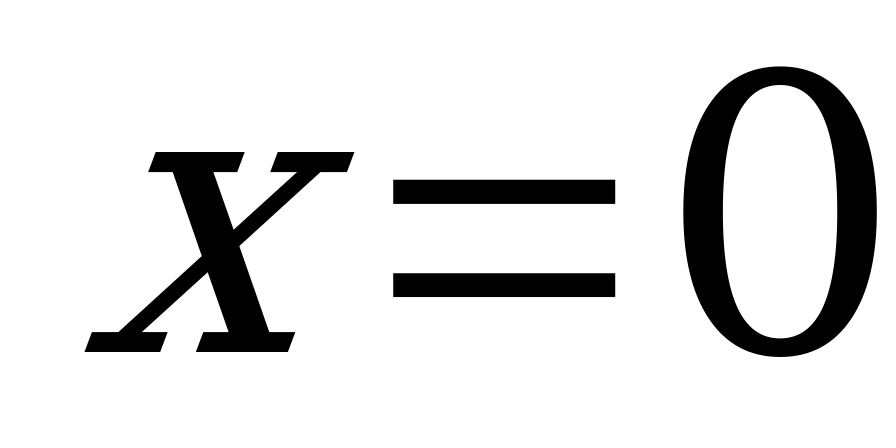 до
до 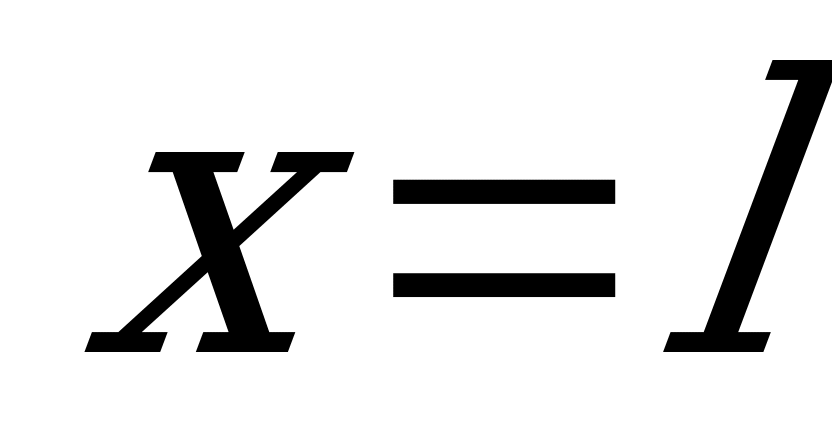 , а второй интеграл – статический момент этой же площади относительно оси
, а второй интеграл – статический момент этой же площади относительно оси 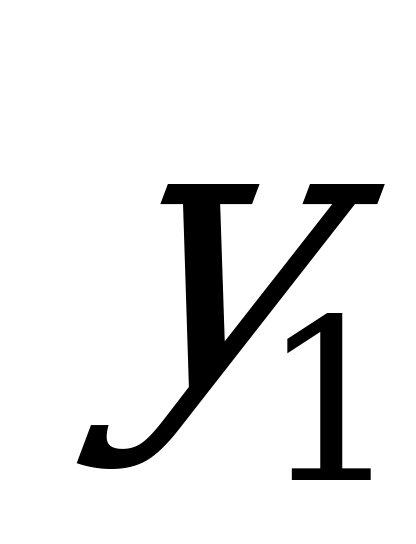 , который, как известно (из формулы
, который, как известно (из формулы 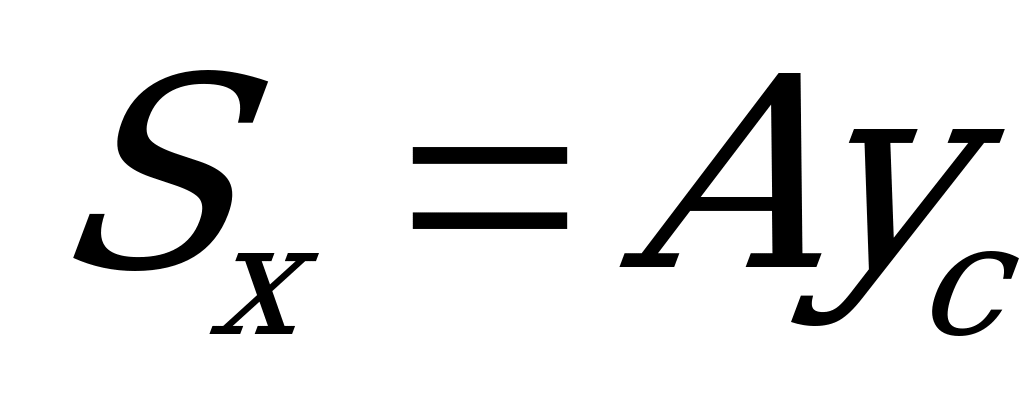 и
и 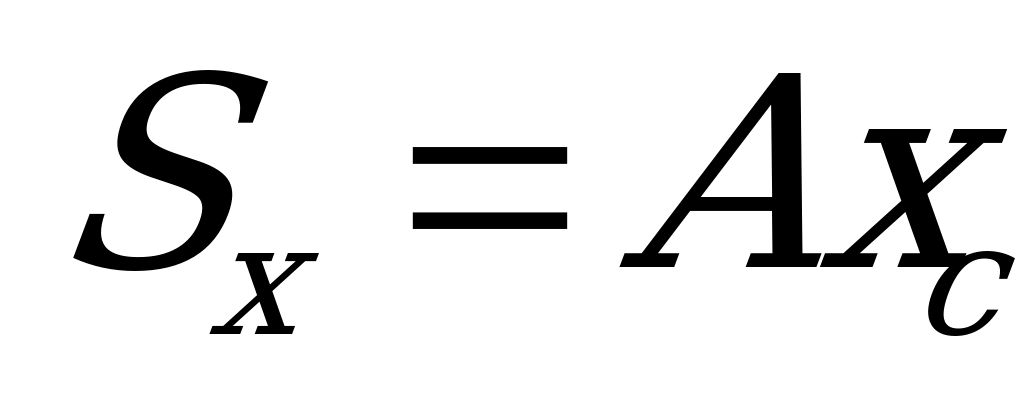 ) , выражается произведением площади на координату
) , выражается произведением площади на координату 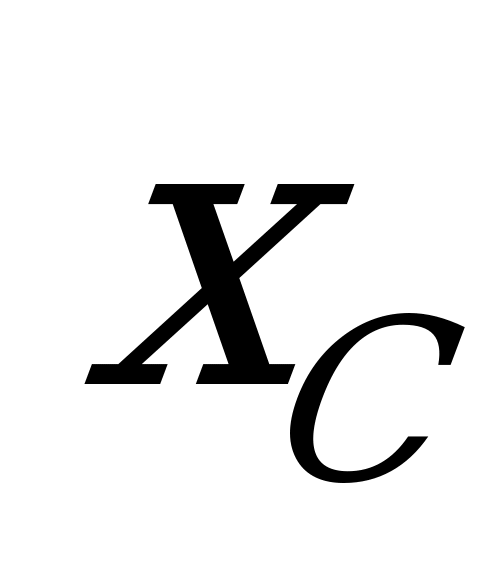 ее центра тяжести С. Если площадь эпюры
ее центра тяжести С. Если площадь эпюры 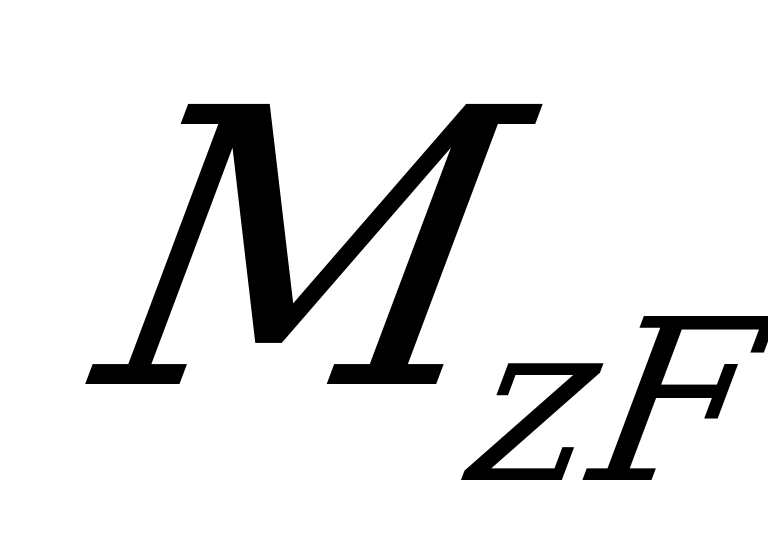 обозначить буквой
обозначить буквой 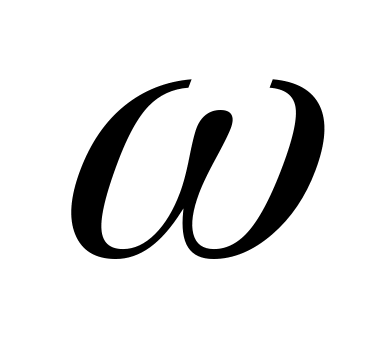 , то равенство (а) примет вид
, то равенство (а) примет вид
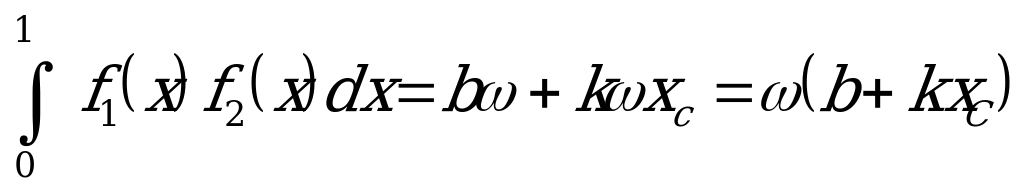 ,
,
где 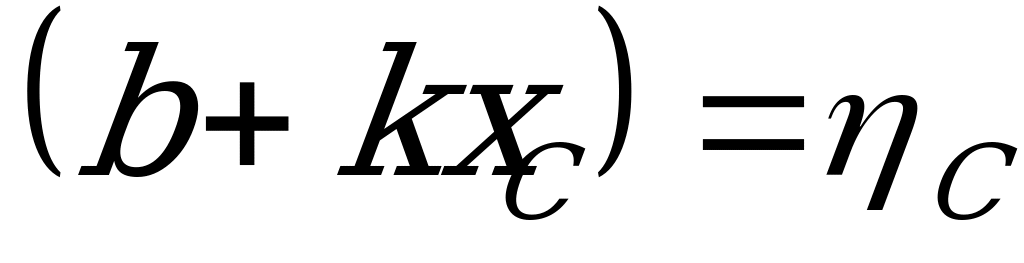 , т.е. ордината эпюры
, т.е. ордината эпюры 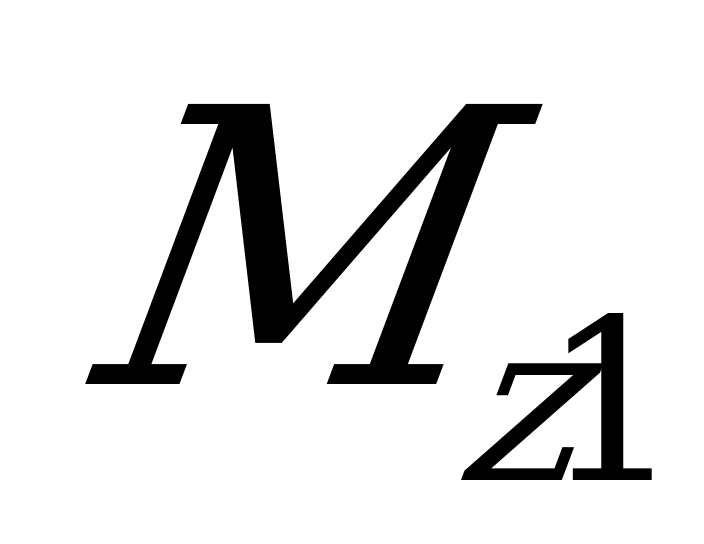 под центром тяжести С эпюры
под центром тяжести С эпюры 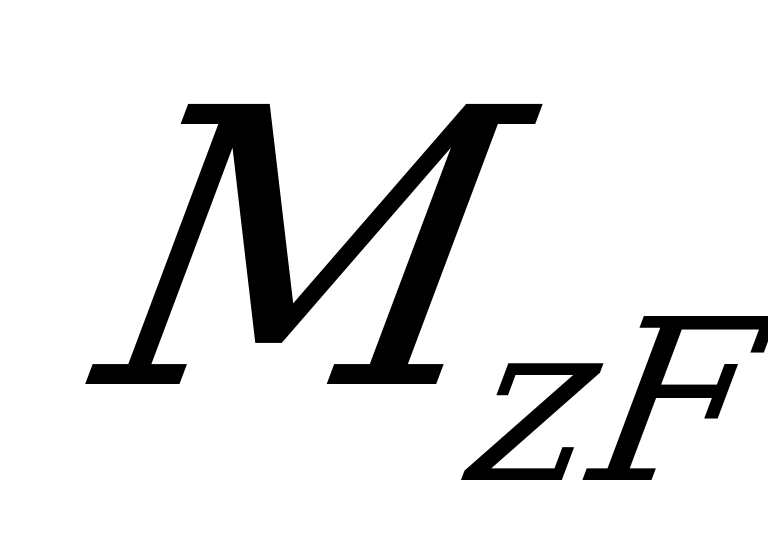 . Следовательно, в окончательном виде
. Следовательно, в окончательном виде
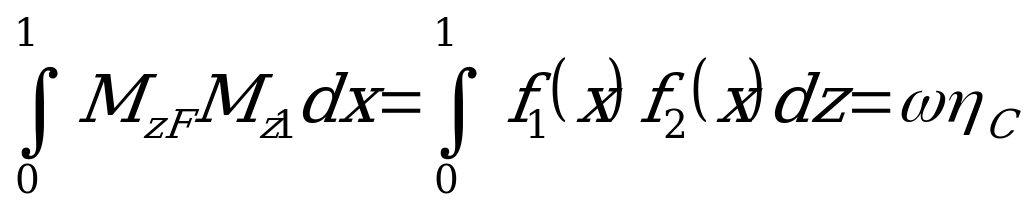 .
.
Теперь формула интеграла Мора 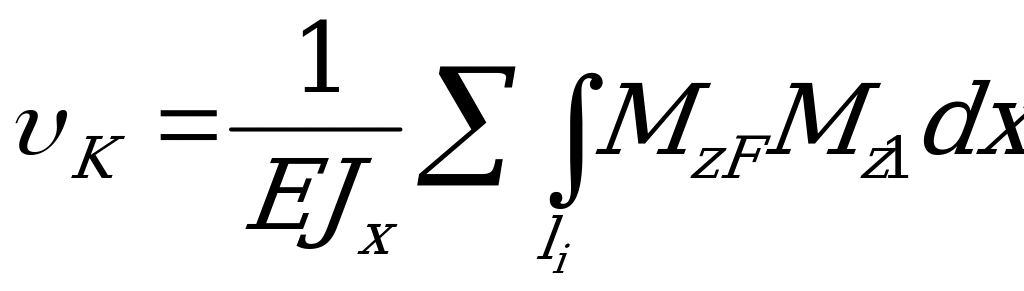 может быть записана так
может быть записана так
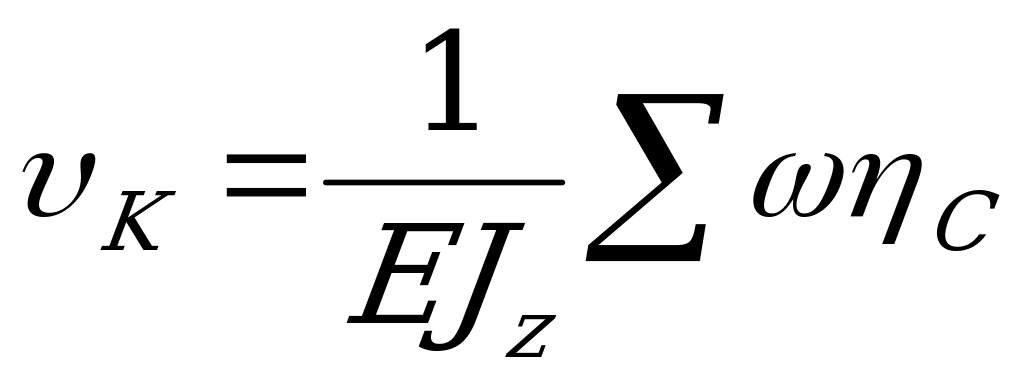 . (2.94)
. (2.94)
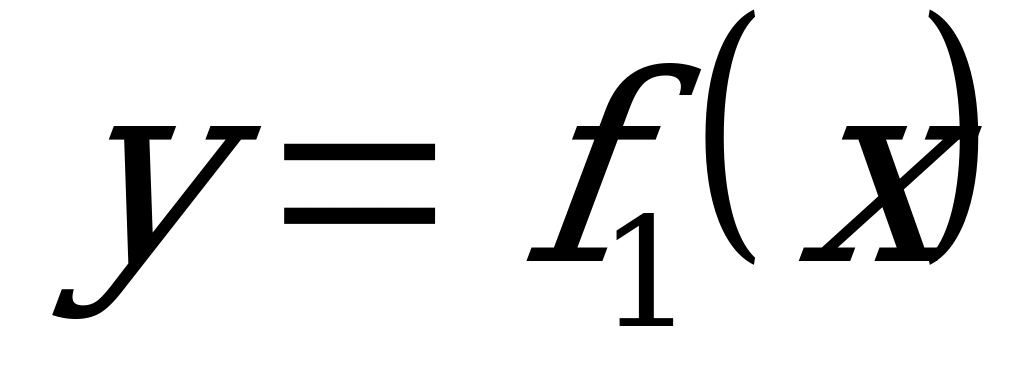
 эпюра
эпюра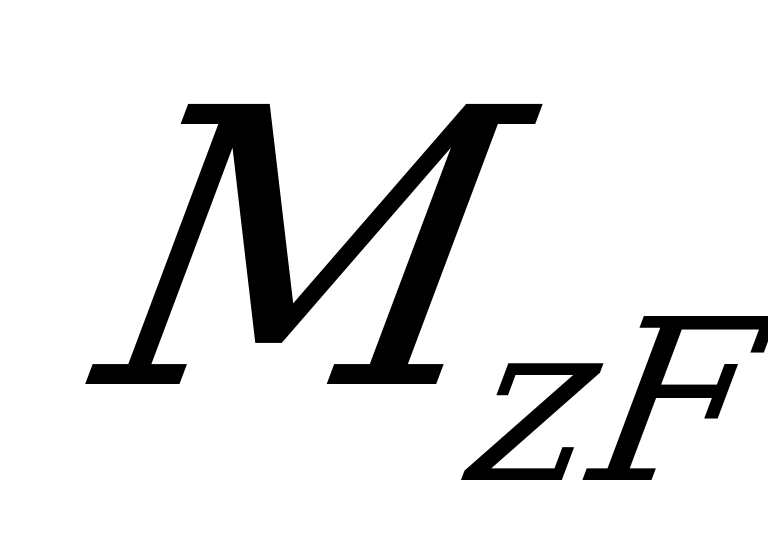



 С
С
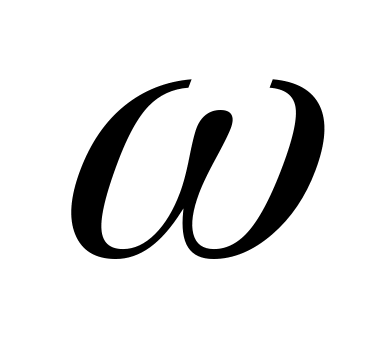


 х
х
0 х dx

 xc
xc

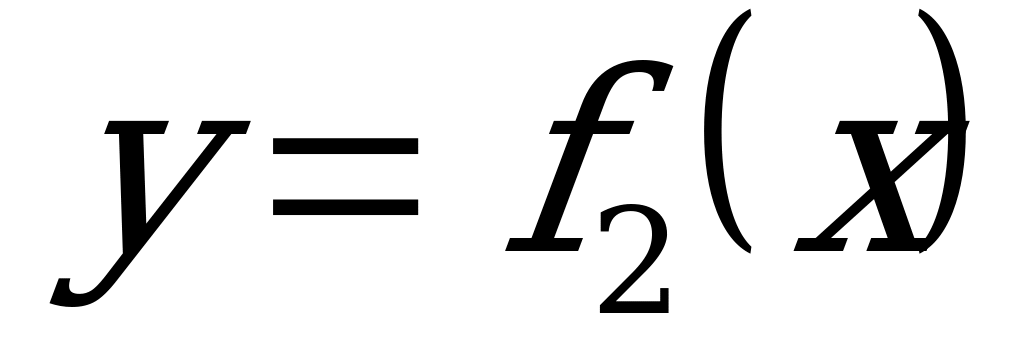


 эпюра
эпюра 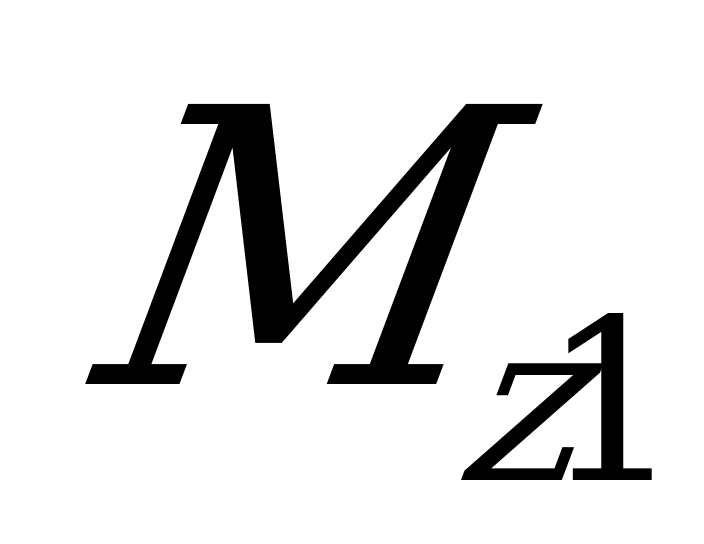

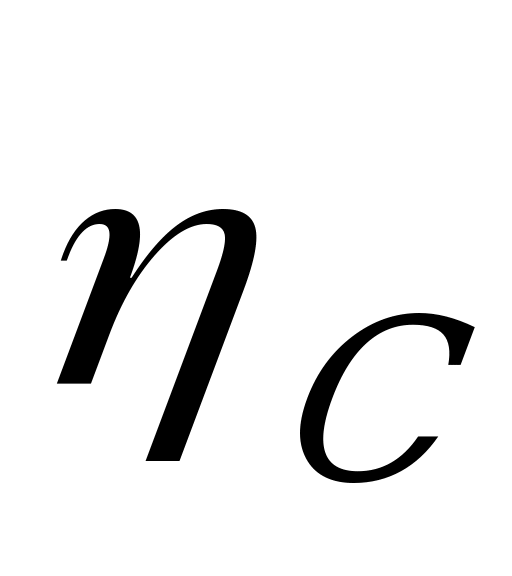
 х
х
0

l
Таким образом, правило Верещагина состоит в том, что интеграл Мора, составленный для каждого из участков нагружения балки, равен произведению площади 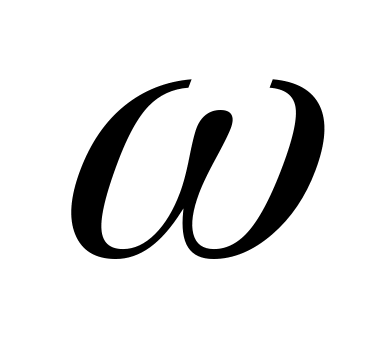 нелинейной эпюры изгибающих моментов
нелинейной эпюры изгибающих моментов 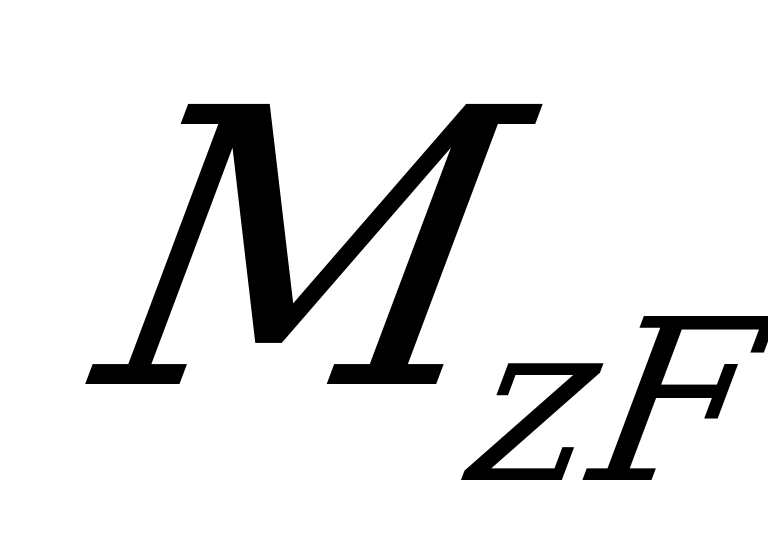 на ординату
на ординату 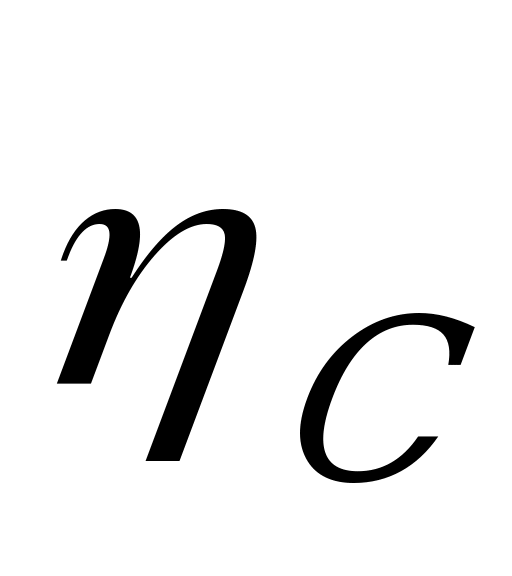 эпюры изгибающего момента
эпюры изгибающего момента 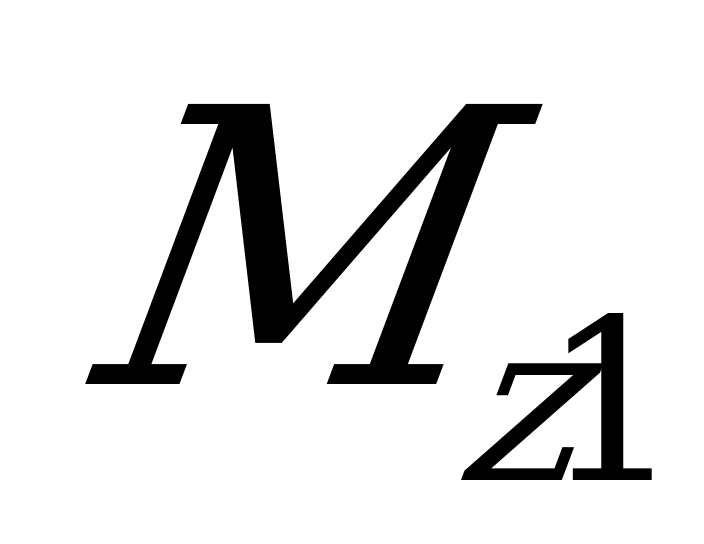 , соответствующую положению центра тяжести площади
, соответствующую положению центра тяжести площади 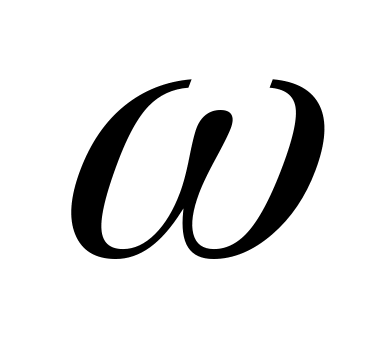 .
.
Расчет тормозных средств.
Тормозные средства поезда должны обеспечивать безопасное движение с установленными скоростями и остановку поезда на длине тормозного пути.
Тормозным путем называется расстояние, которое проходит поезд от начала торможения до полной остановки.
Полный, или расчетный, тормозной путь
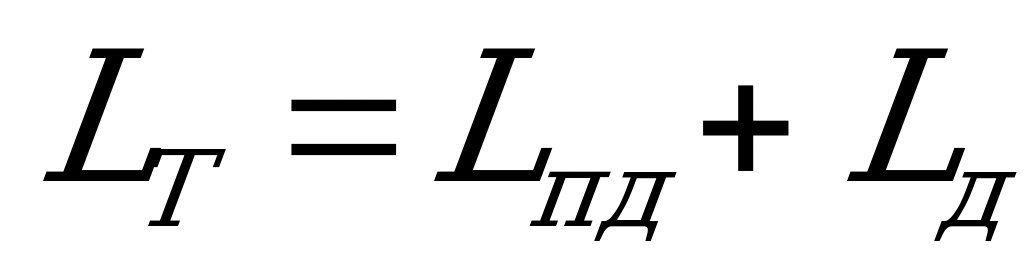 ,
,
где 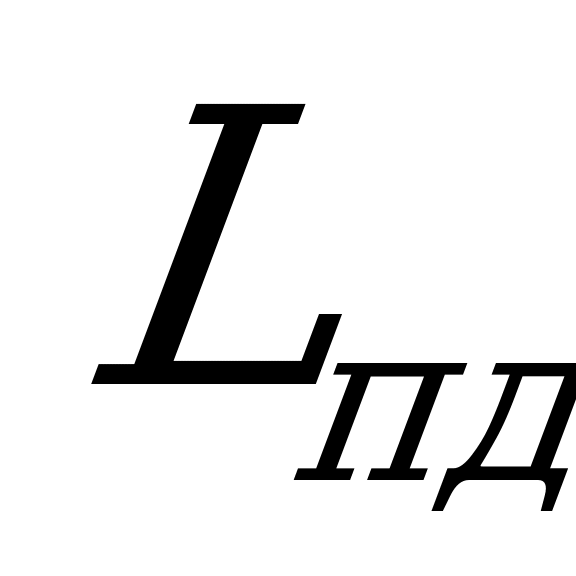 - предтормозной путь, проходимый поездом за время приведения тормозов в действие , м. Определяется временем приведения тормозов в действие
- предтормозной путь, проходимый поездом за время приведения тормозов в действие , м. Определяется временем приведения тормозов в действие 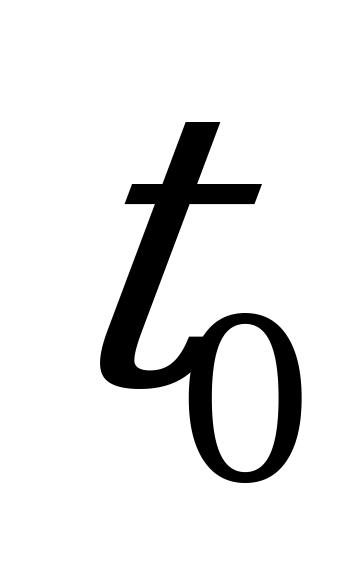 и скоростью движения в течение этого времени
и скоростью движения в течение этого времени 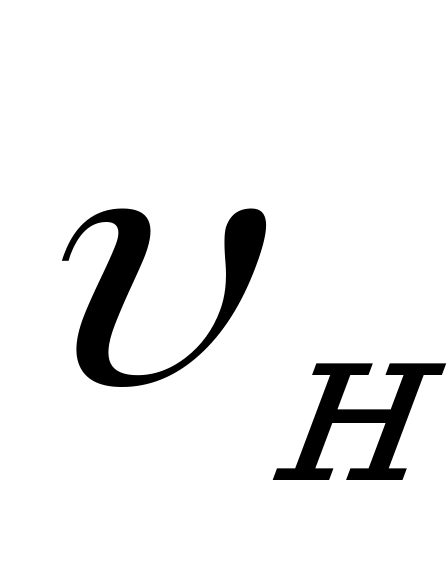 .
.
Для магистральных железных дорог при уклонах до 20% предтормозной путь принято рассчитывать по формуле
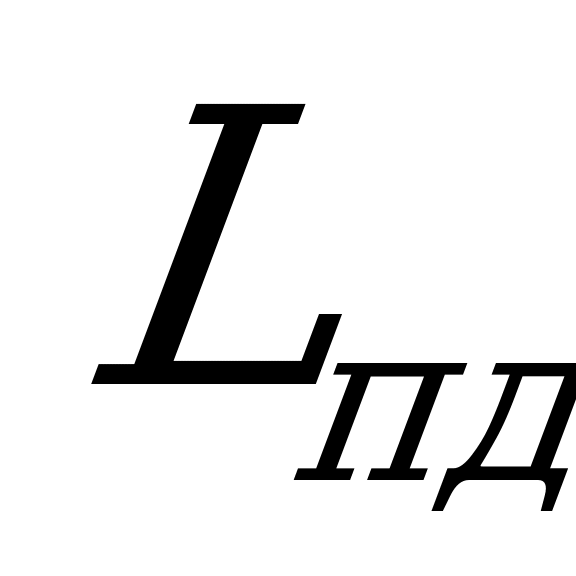 =
=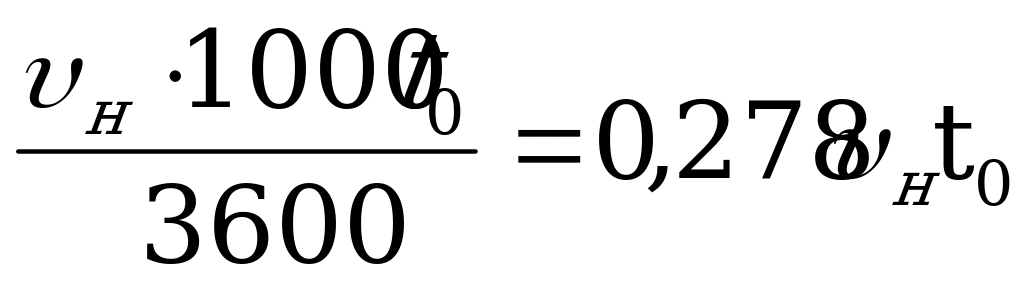 .
.
При тормозах грузового типа и экстренном торможении 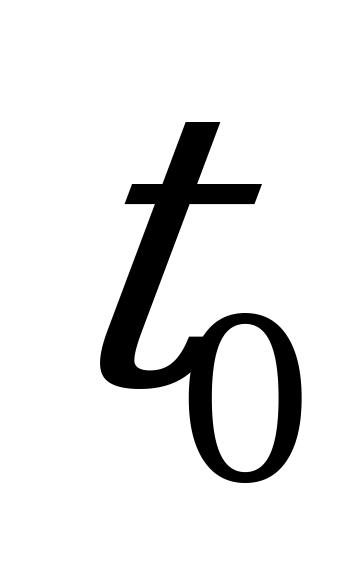 =7с, при служебном торможении – 13с.
=7с, при служебном торможении – 13с.
При движении по крутым уклонам, как это имеет место в карьерах, следует учитывать, что за время приведения тормозов в действие скорость движения увеличивается и, следовательно, увеличивается предтормозной путь, тогда
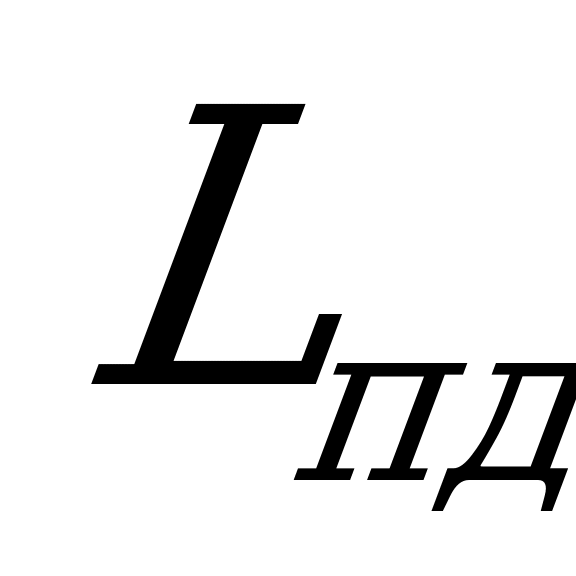 =
=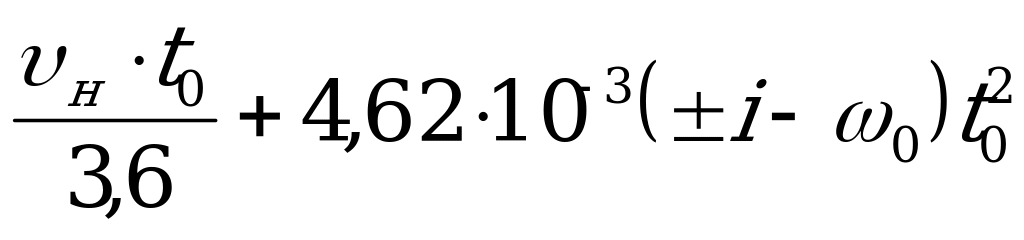 .
.
Действительный путь торможения 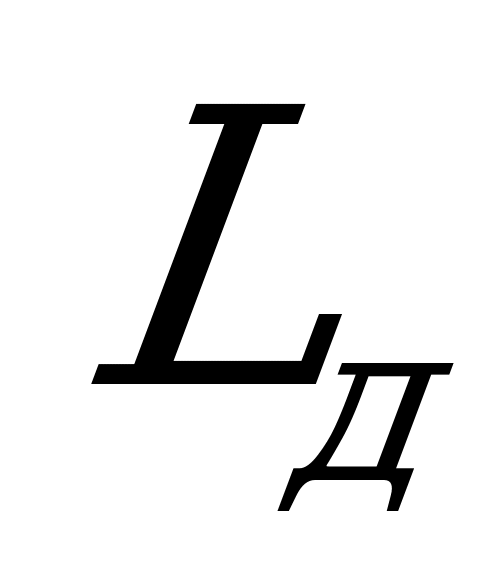 устанавливается при решении уравнения движения методом приближенного аналитического интегрирования. Метод заключается в том, что в уравнении движения поезда вместо бесконечно малых приращений скорости принимают конечные малые превращения и в их пределах величину ускоряющей силы считают постоянной.
устанавливается при решении уравнения движения методом приближенного аналитического интегрирования. Метод заключается в том, что в уравнении движения поезда вместо бесконечно малых приращений скорости принимают конечные малые превращения и в их пределах величину ускоряющей силы считают постоянной.
Принимая силу 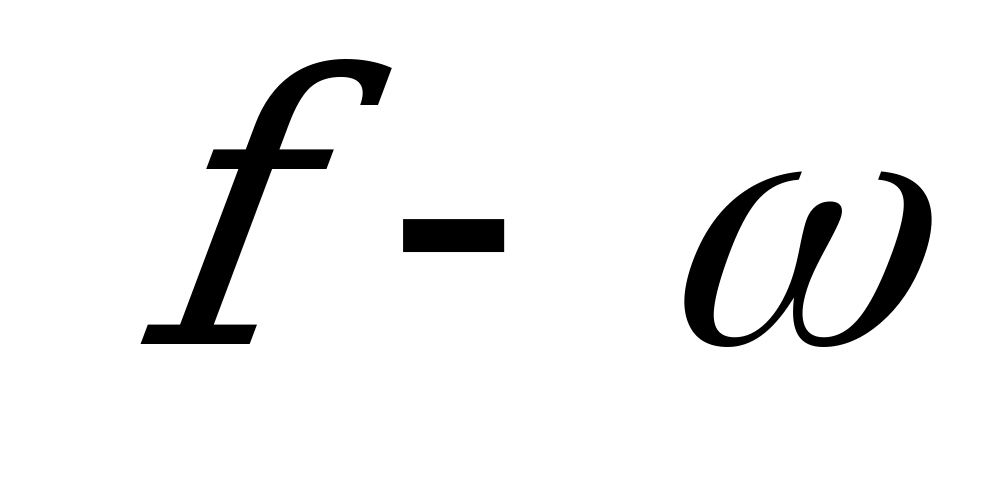 в пределах скорости
в пределах скорости 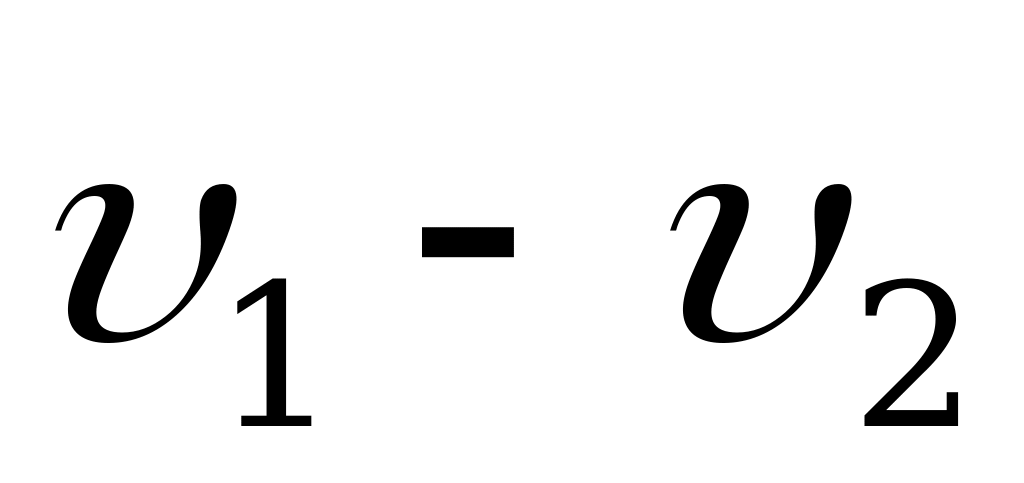 постоянной, получаем зависимость скорости от расстояния
постоянной, получаем зависимость скорости от расстояния 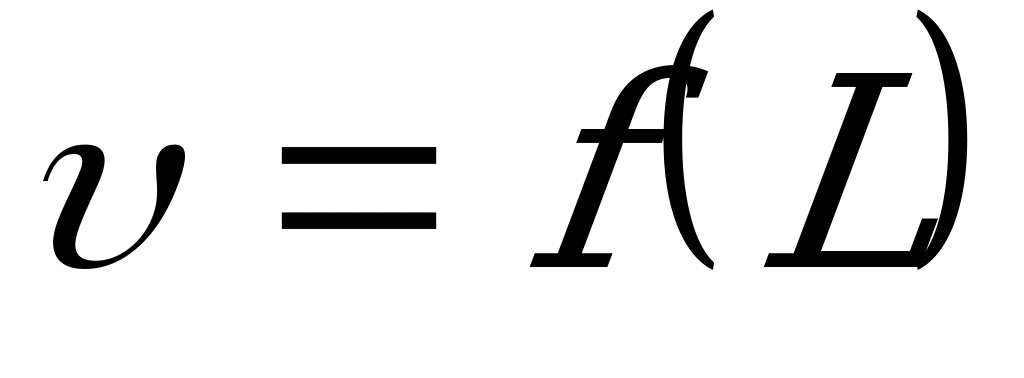 :
:
LД=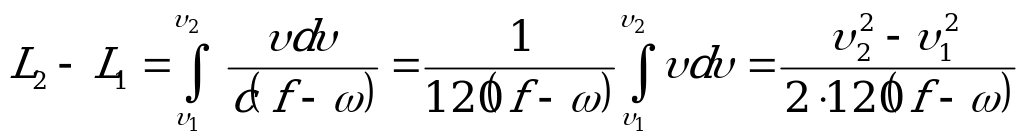 .
.
Считая 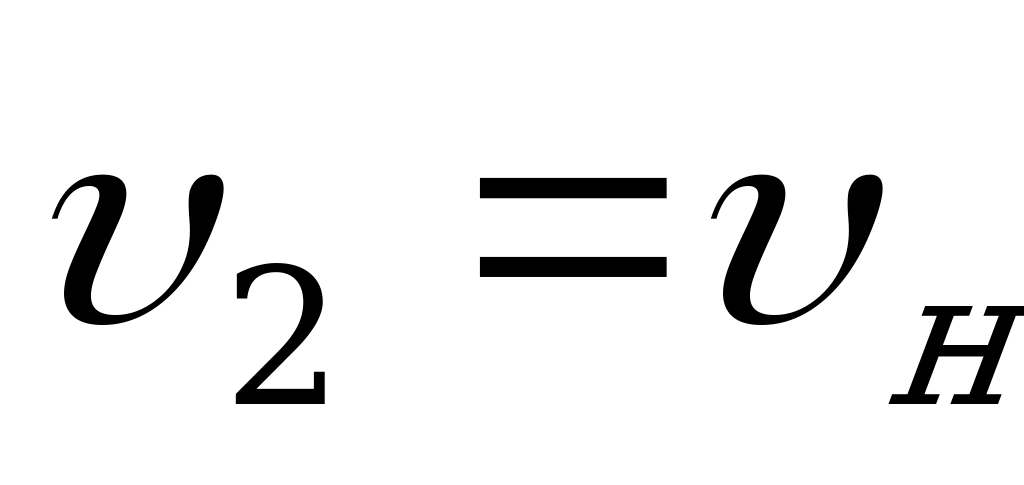 и
и 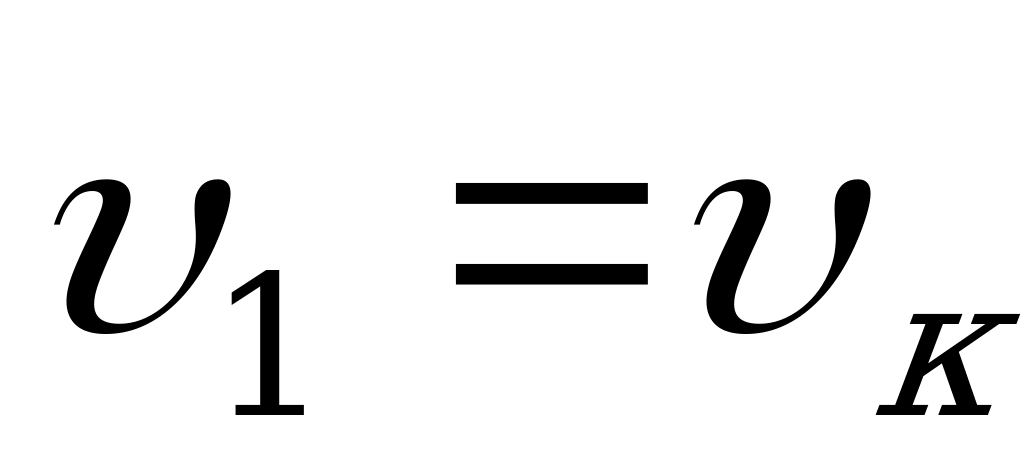 - соответственно начальная и конечная скорость движения (к/ч), имеем
- соответственно начальная и конечная скорость движения (к/ч), имеем
LД =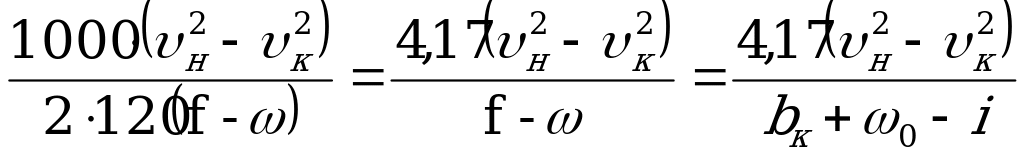 ,
,
где 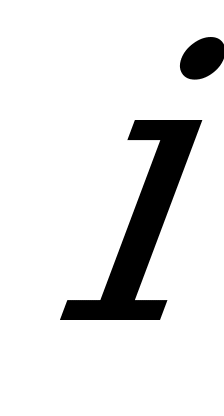 - величина уклона, на котором производится торможение.
- величина уклона, на котором производится торможение.
При торможении до остановки 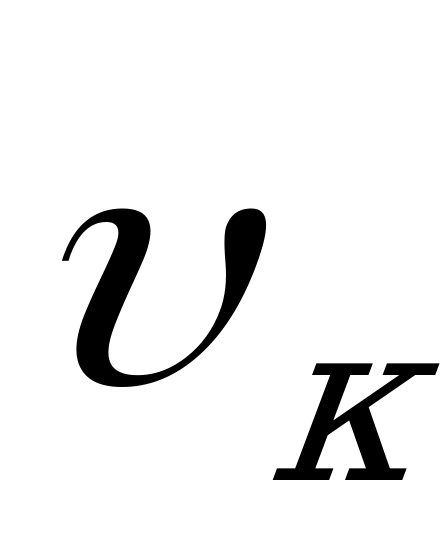 = 0.
= 0.
Окончательно
LД = 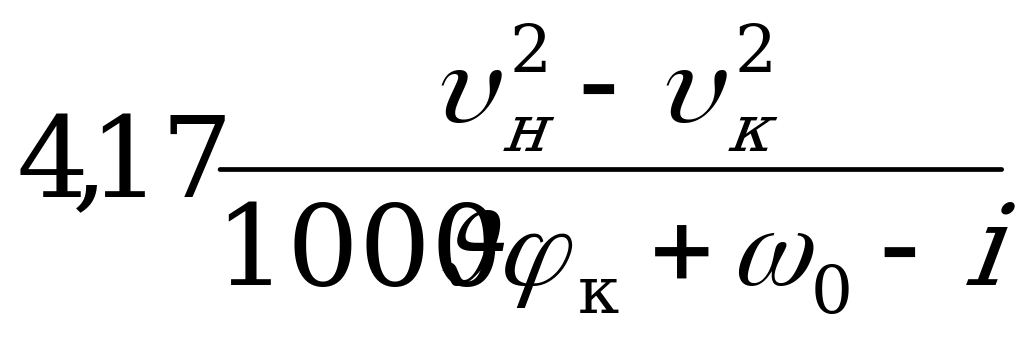 .
.
Кинематика и условия подбора чисел
зубьев планетарных передач
При исследовании кинематики планетарных механизмов широка используется метод обращенного движения, или метод Виллиса. Этот метод заключается в сообщении всем звеньям механизма дополнительной угловой скорости 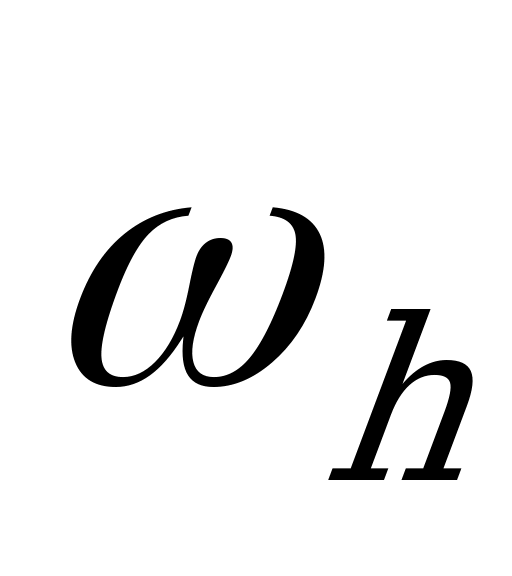 с обратным знаком, в результате чего происходит остановка водила
с обратным знаком, в результате чего происходит остановка водила 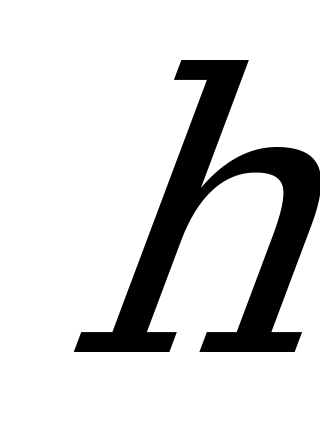 . Примем изложенный метод к планетарному механизму, изображенному на рисунке 5.1.
. Примем изложенный метод к планетарному механизму, изображенному на рисунке 5.1.
5.1.
Дл получения передачи с невращающимся водилом можно записать
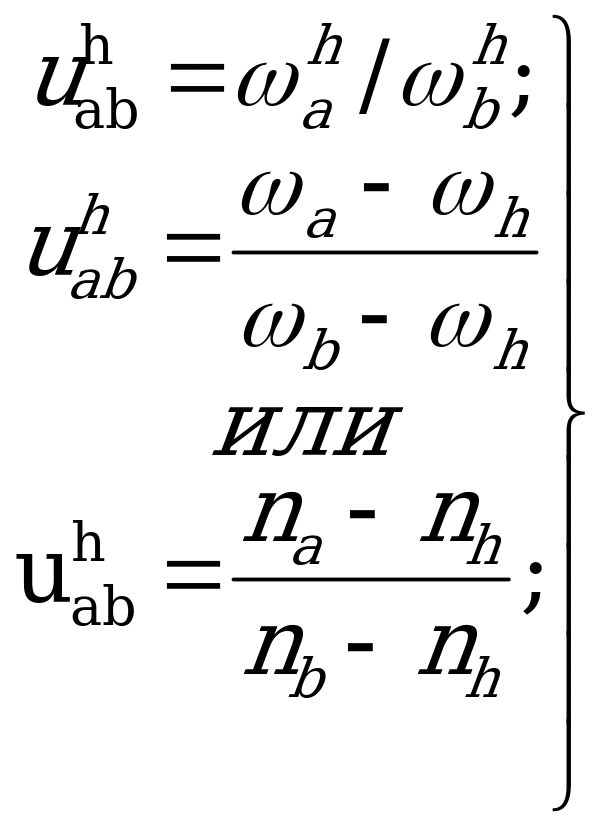 5.1.
5.1.
где 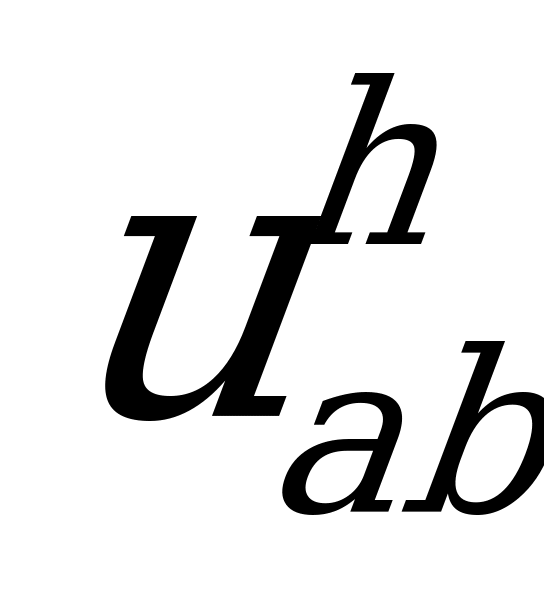 - передаточное отношение, связывающее угловые скорости центральных колес при неподвижном водиле (передаточное отношение передачи с остановленным водилом);
- передаточное отношение, связывающее угловые скорости центральных колес при неподвижном водиле (передаточное отношение передачи с остановленным водилом); 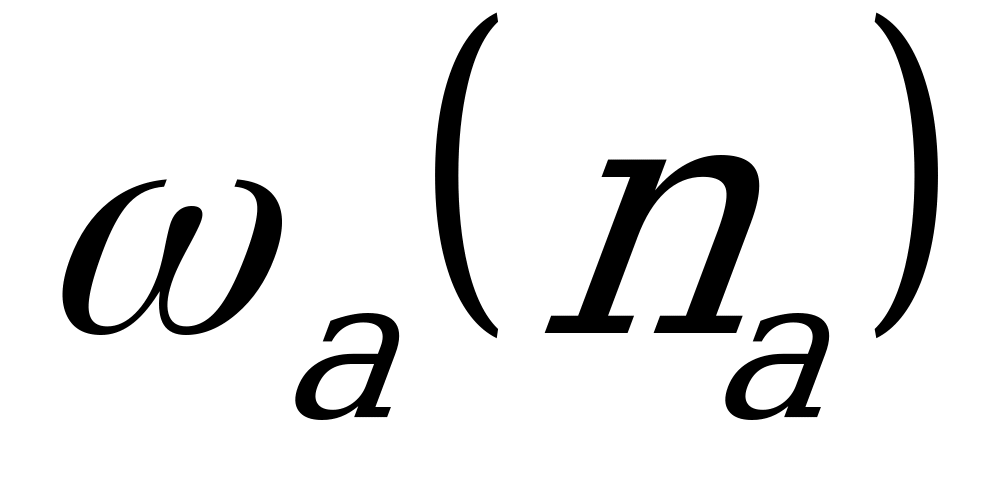 - угловая скорость (частота вращения) звена а;
- угловая скорость (частота вращения) звена а; 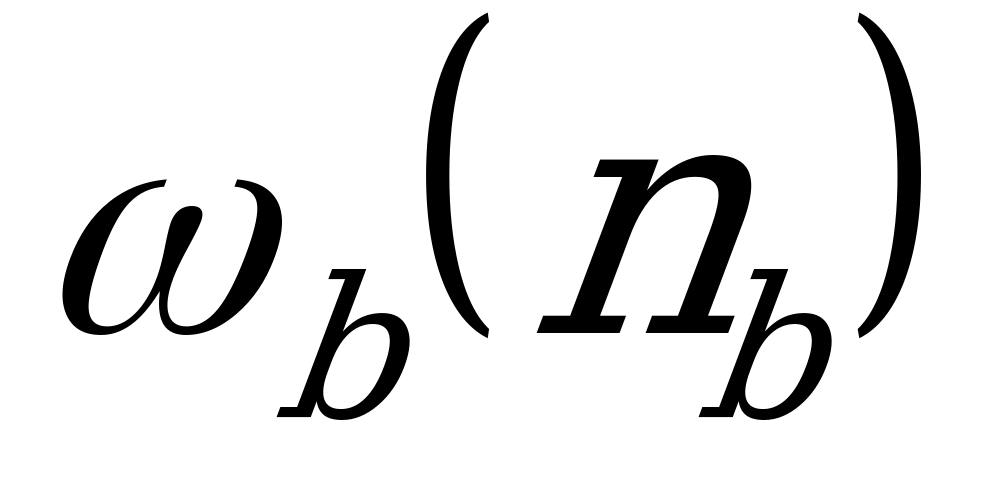 - угловая скорость (частота вращения звена
- угловая скорость (частота вращения звена 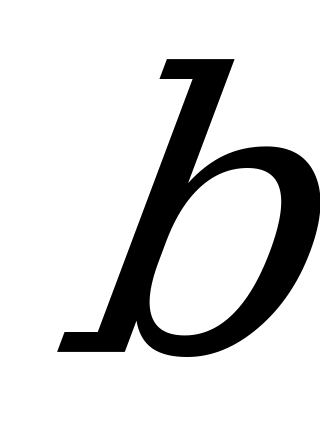 ;
; 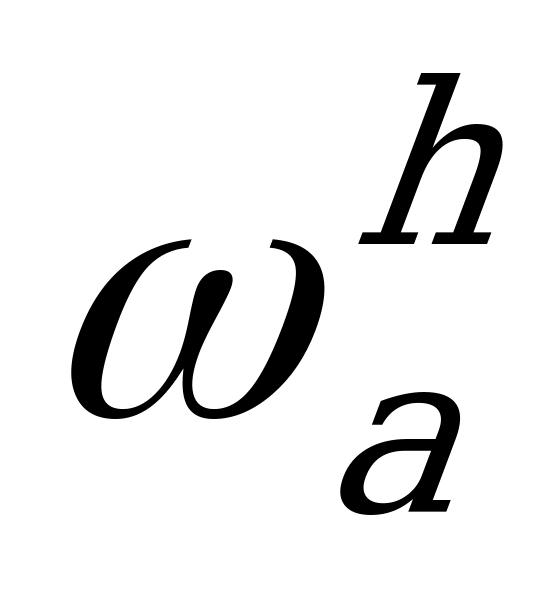 - угловая скорость звена а при оставленном водиле
- угловая скорость звена а при оставленном водиле 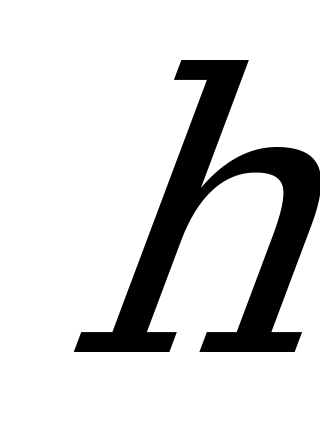 , и т.д.
, и т.д.
Выражение (5.1) носит название формулы Виллиса.
5.2. Определение угловых скоростей
| Абсолютная угловая скорость | Относительная угловая скорость в обращенном движении |
| 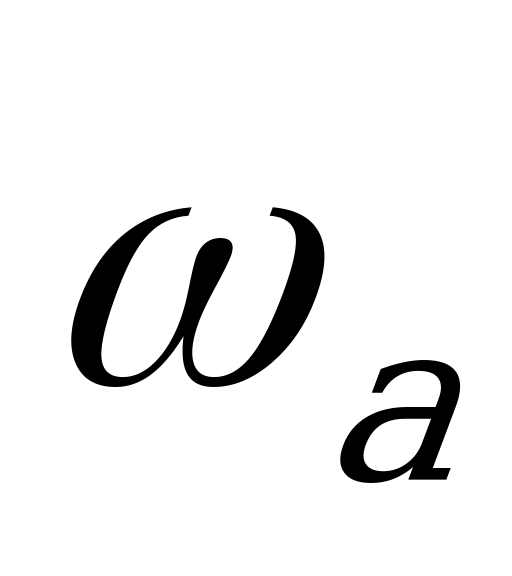
| 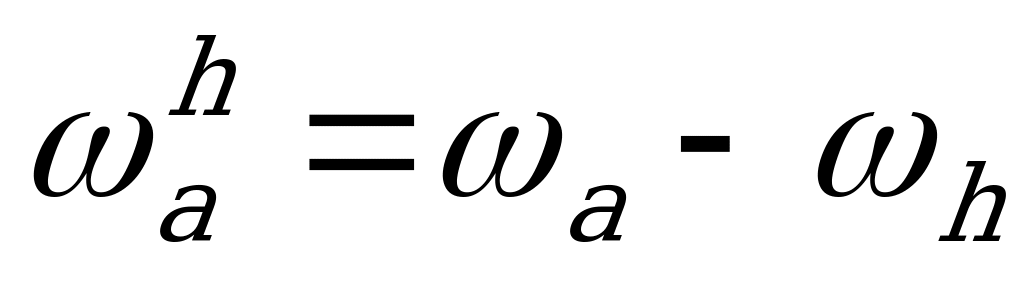
|
| 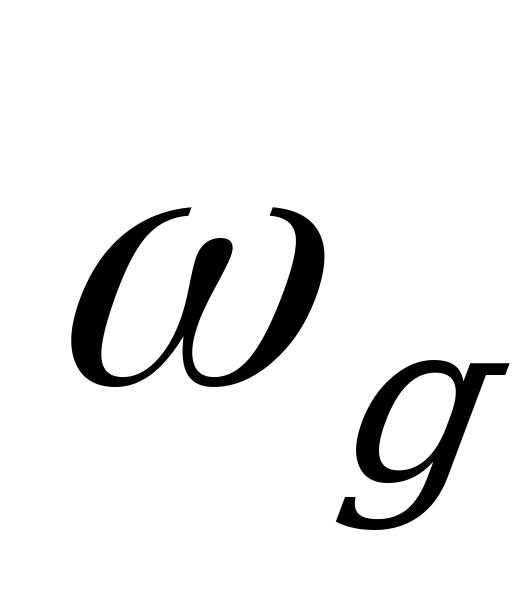
| 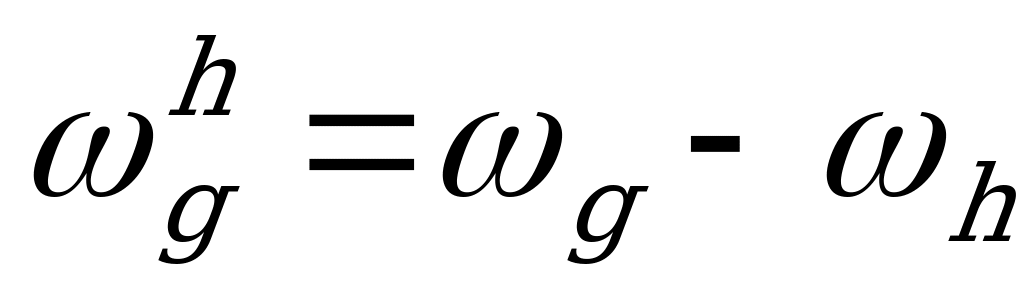
|
| 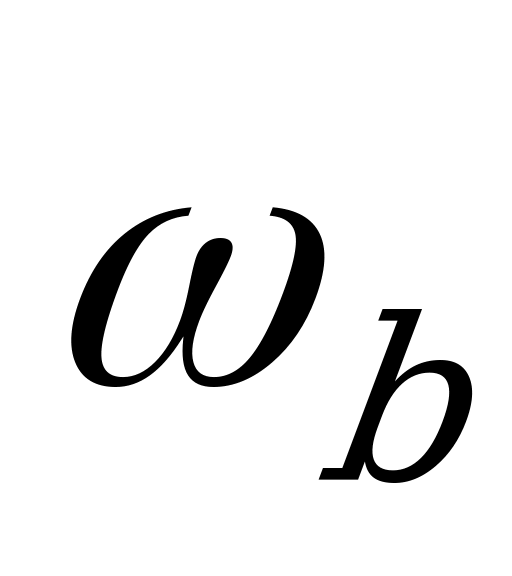
| 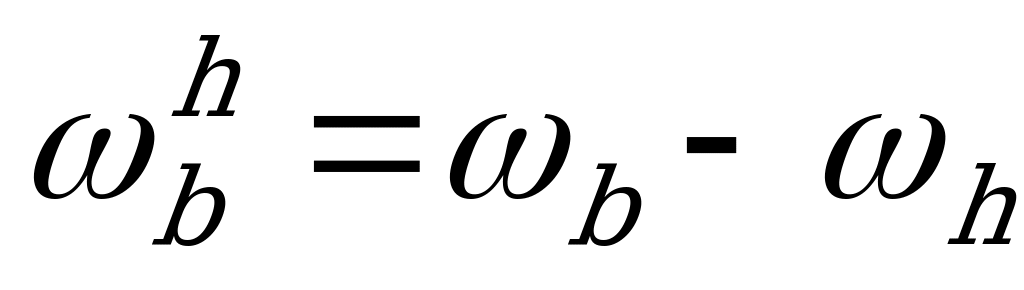
|
| 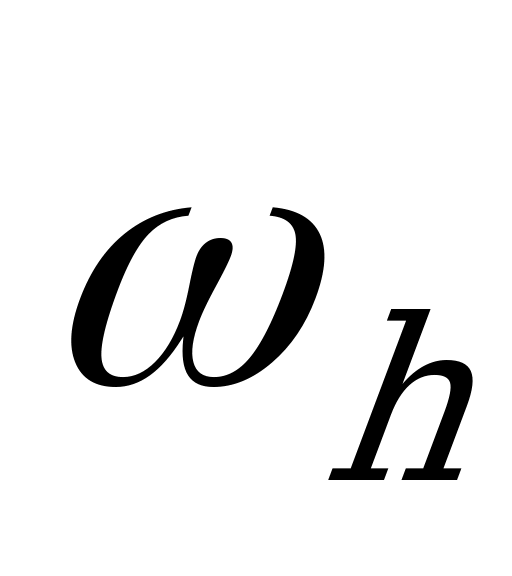
| 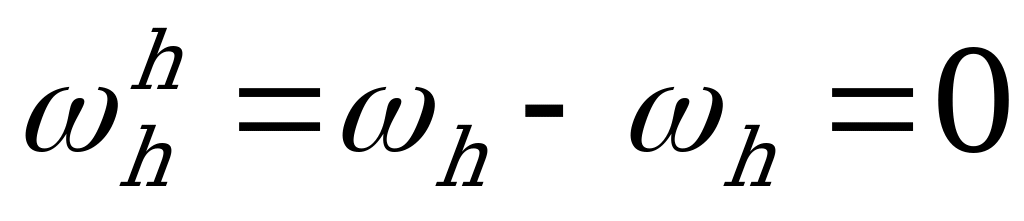
|
Предположим, что в механизме, приведенном на рис. 5.1., 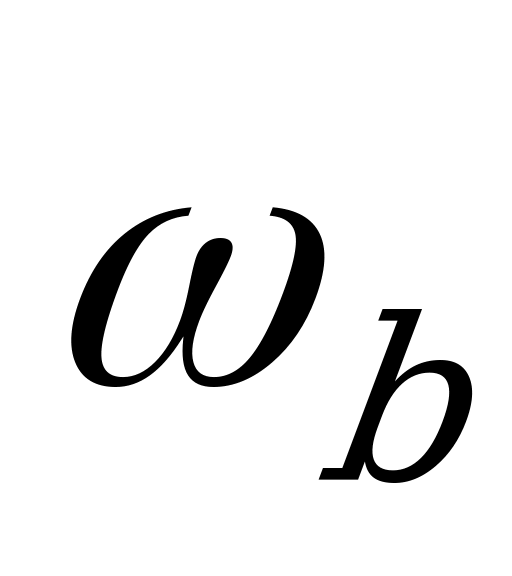 =0 – простая планетарная передача, соответствующая варианту 1 (табл. 5.1).
=0 – простая планетарная передача, соответствующая варианту 1 (табл. 5.1).
Условия подбора чисел зубьев планетарных передач.
При выборе чисел зубьев колес в многосателлитовой планетарной передаче должны быть соблюдены следующие три условия:
а) соосности – совпадения осей ведущего и ведомого валов;
б) соседства – установление максимального числа сателлитов при отсутствии касания их окружностей выступов;
в) сборки – связь числа зубьев колеса с числом сателлитов при равномерном распределении их осей по окружности.
Условие соосности для различных вариантов передач(5.2):
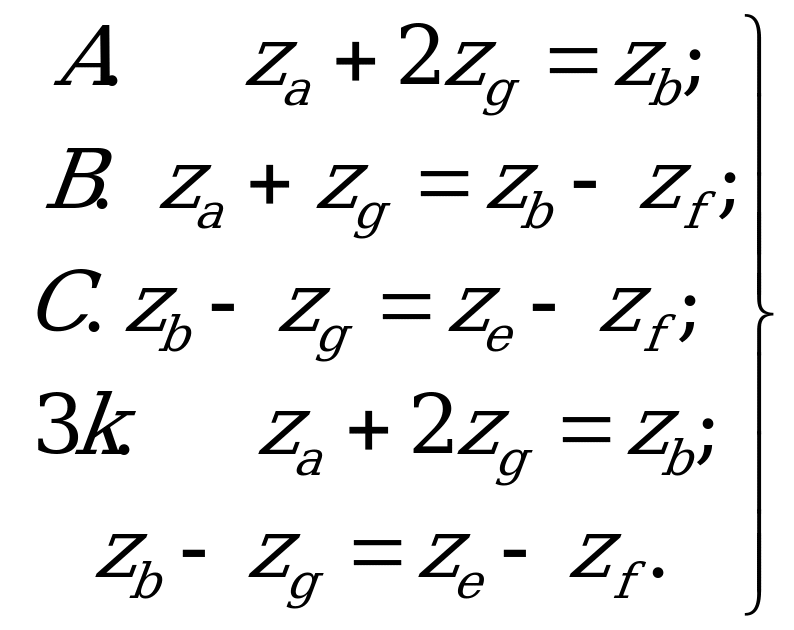 (5.3)
(5.3)
Для обеспечения зазора между сателлитами должно выполняться условие соседства, которое заключается в том, что сумма радиусов окружностей выступов 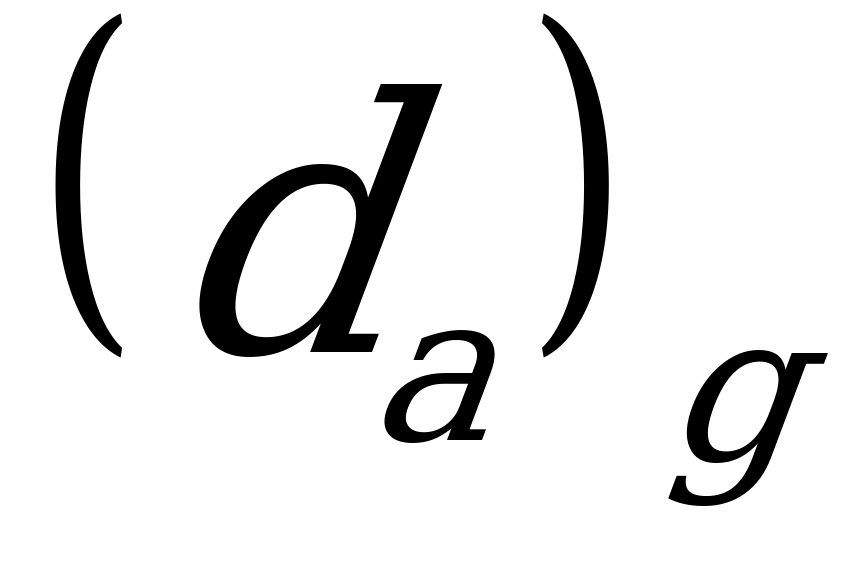 соседних сателлитов должна быть меньше расстояния между осями
соседних сателлитов должна быть меньше расстояния между осями 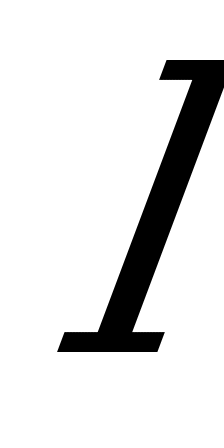 (5.1.), т.е.
(5.1.), т.е.
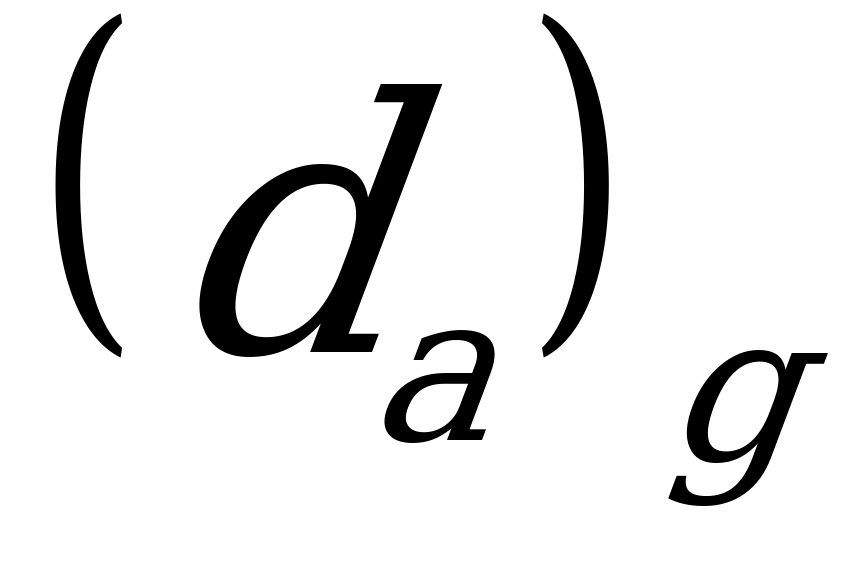
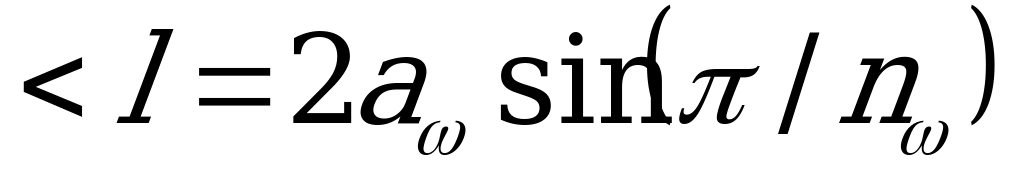 . (5.4)
. (5.4)
Минимально допустимую разность 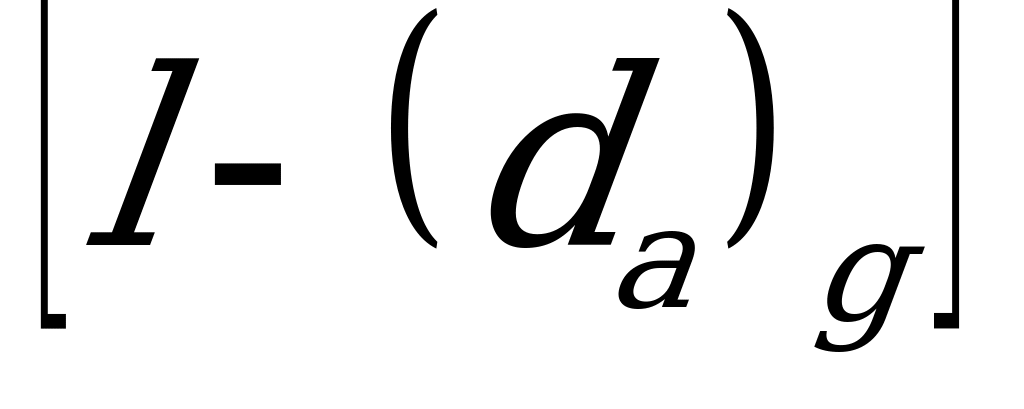 можно принять равной приблизительно 0,5m.
можно принять равной приблизительно 0,5m.
Выполнение условия соосности достаточно для обеспечения сборки передачи с 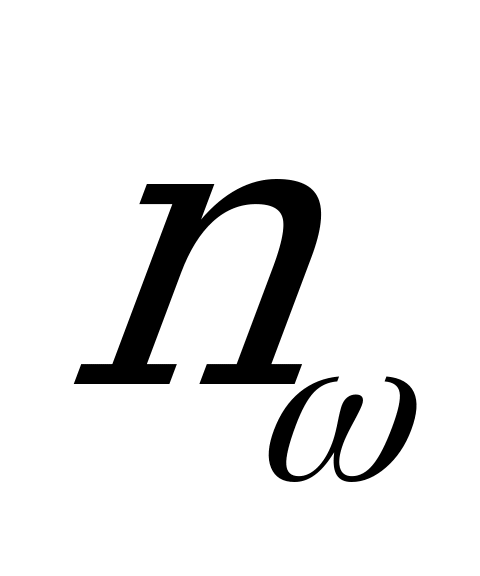 . При
. При 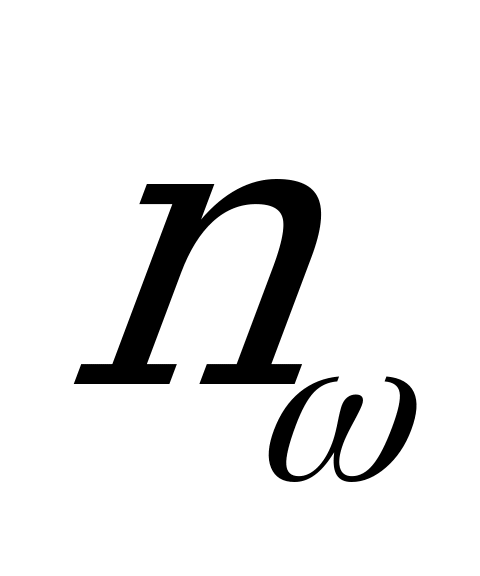
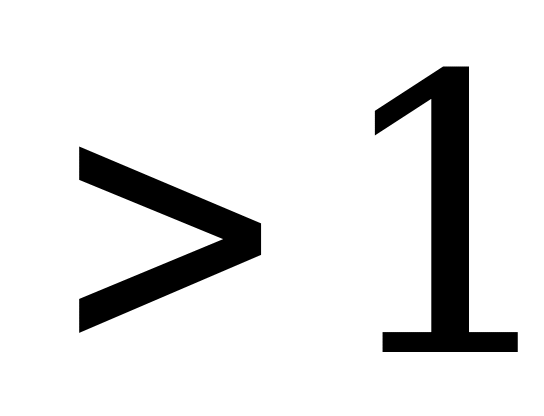 имеются дополнительные условия, ограничивающие выбор чисел зубьев планетарных передач в зависимости от числа сателлитов. Это дополнительное условие носит название условие сборки и выражается целым числом
имеются дополнительные условия, ограничивающие выбор чисел зубьев планетарных передач в зависимости от числа сателлитов. Это дополнительное условие носит название условие сборки и выражается целым числом 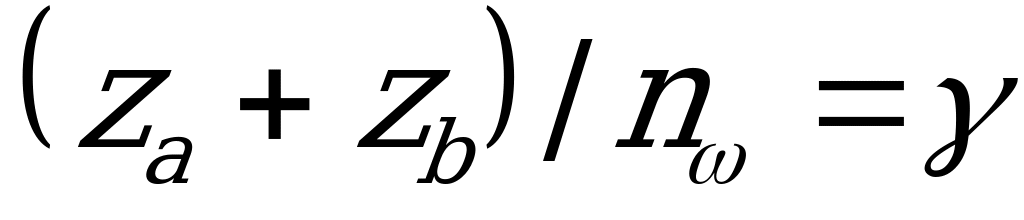 , т.е. сумма чисел зубьев центральных колес должна быть кратной
, т.е. сумма чисел зубьев центральных колес должна быть кратной 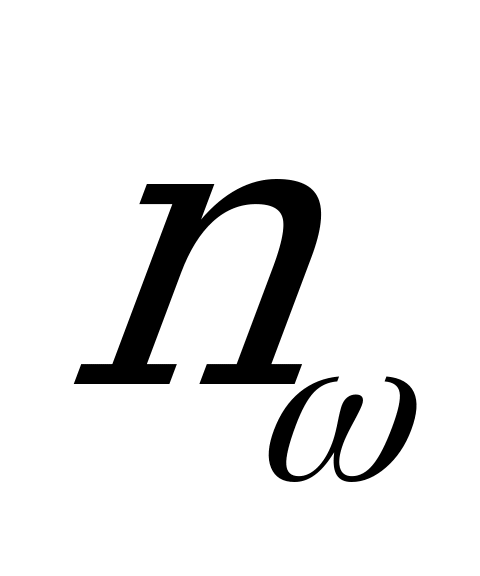 .
.







 y M
y M 600
600
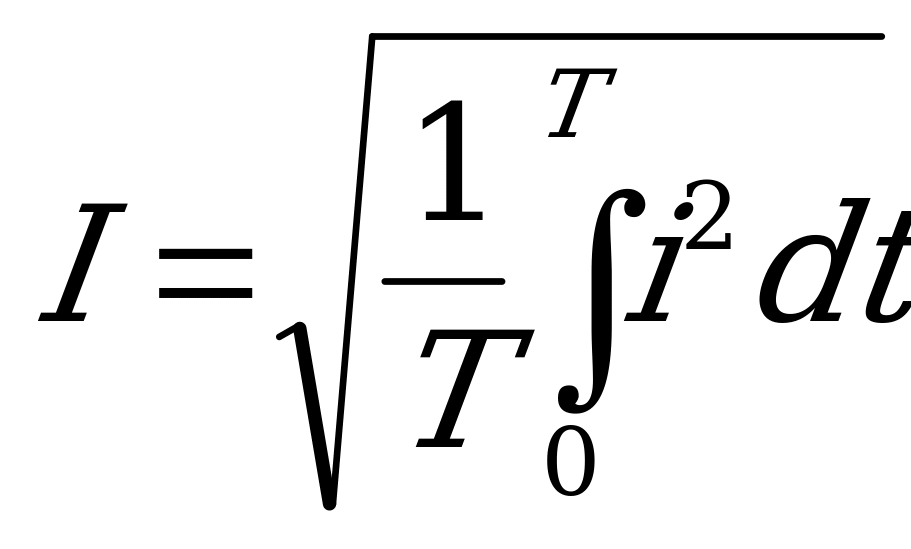 .
.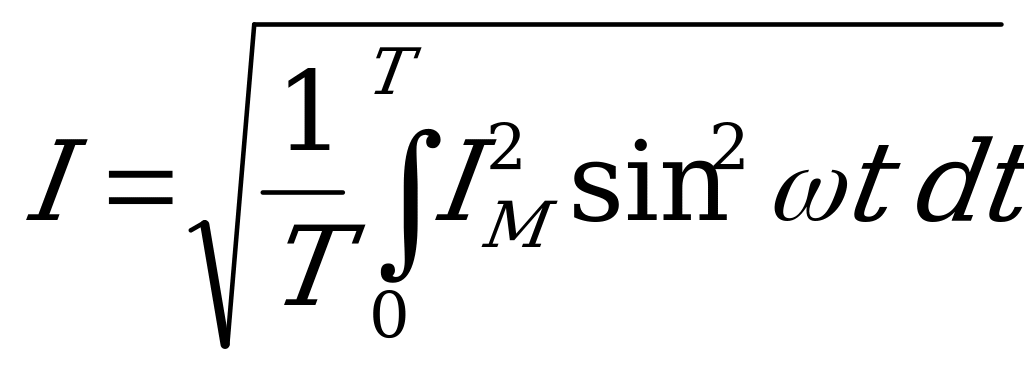 .
.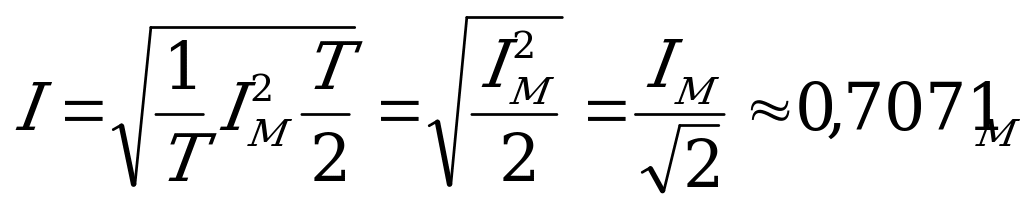 .
. i
i



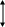

 0
0
 .
. Y B
Y B





 EM2
EM2 
 e2 Б
e2 Б




 Г Х
Г Х 0
0 










 y x
y x



 xC
xC

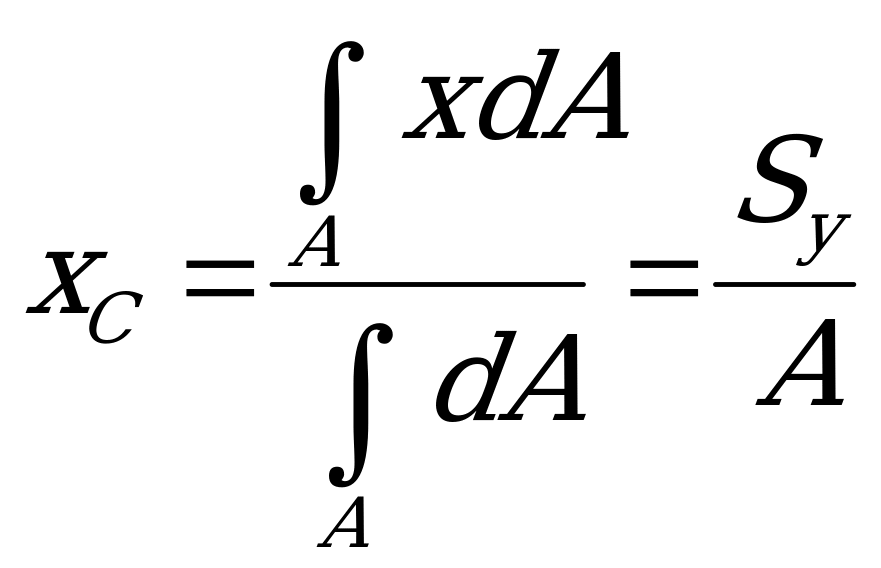 ;
; 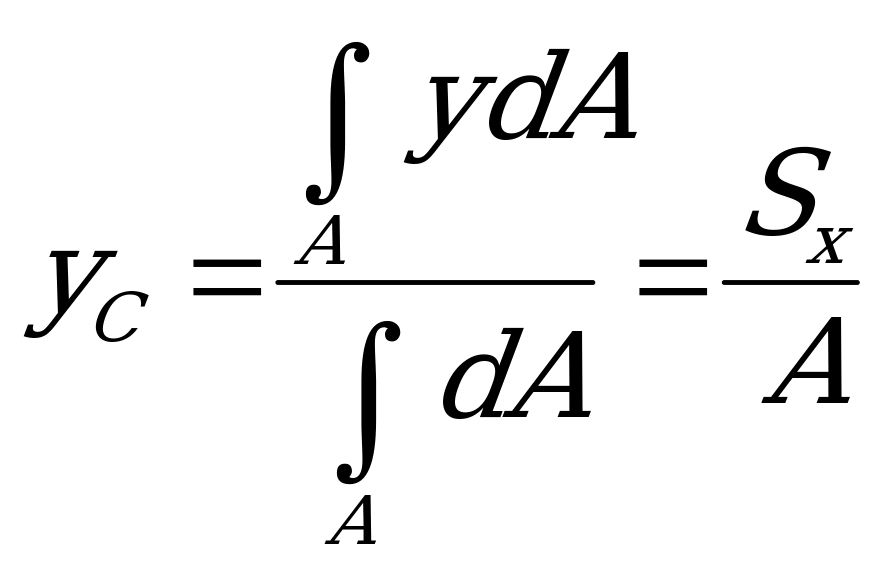 (1.69)
(1.69) y
y  y=ax2
y=ax2








 h=ab2
h=ab2




 y
y 



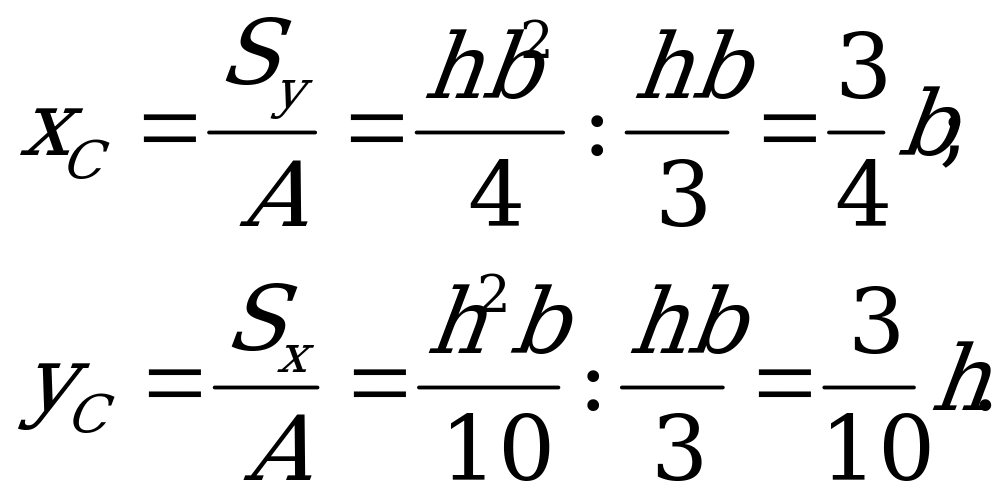







 zC
zC



 c
c  1.178
1.178












 y
y 



 у
у y1 х1
y1 х1  х
х е1
е1 

 С х
С х 
 y
y







 B F
B F
 d θ K1
d θ K1 

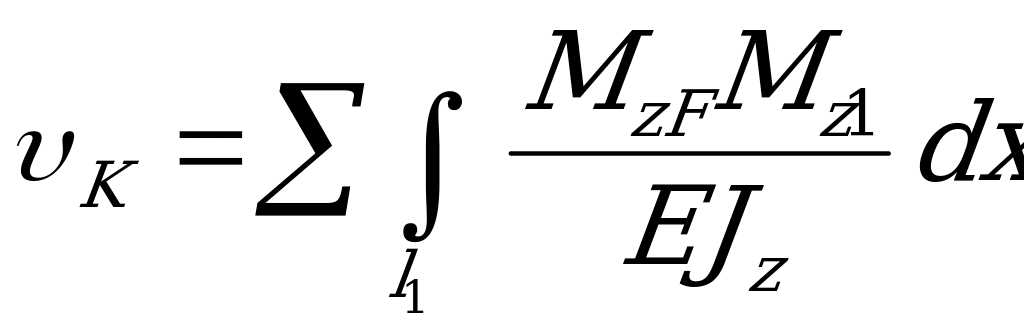 . (2.91)
. (2.91) а) F
а) F





 эпюра
эпюра

 С
С
 эпюра
эпюра 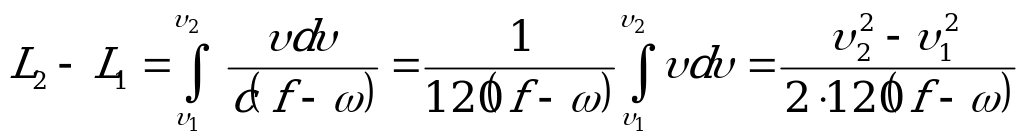 .
.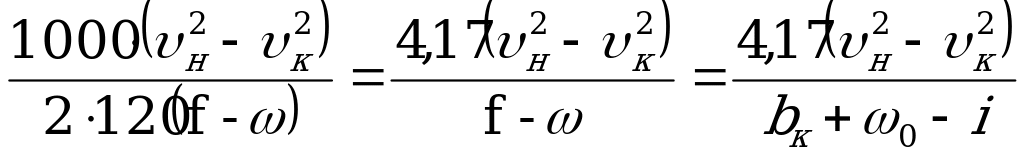 ,
,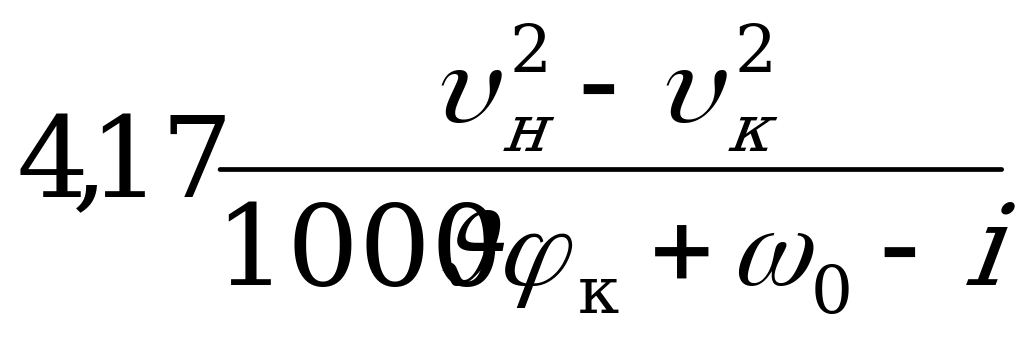 .
.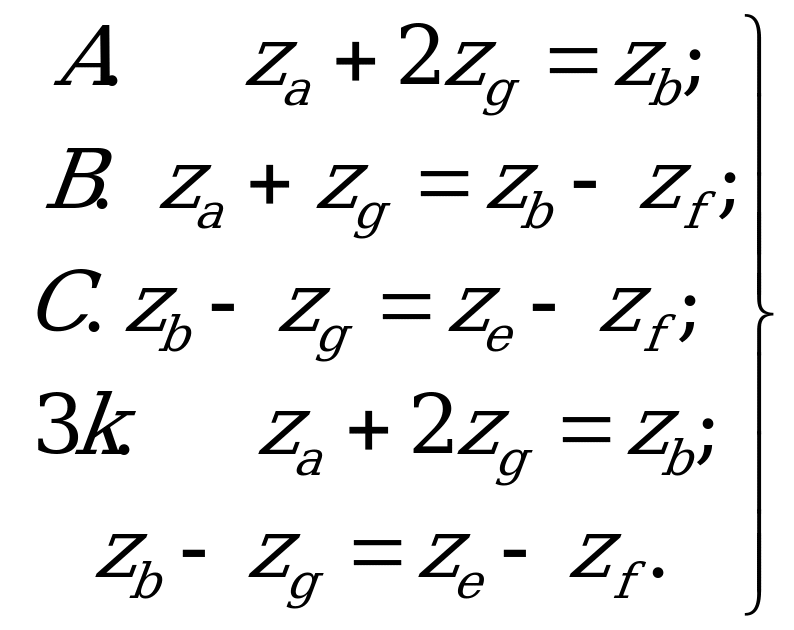 (5.3)
(5.3)

















