Россия, Певек
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 12.10.2019 11:26
Вестман Ольга Николаевна
учитель информатики
69 лет
19 474
1 233 
Местоположение
Специализация
Задание 16 (презентация по типам задач к ЕГЭ)
Категория:
Информатика
27.03.2017 06:40
Просмотр содержимого документа
«Задание 16 (презентация по типам задач к ЕГЭ)»
ege16 ( повышенный уровень, время – 2 мин )
Тема: Кодирование чисел. Системы счисления.
Что нужно знать:
- принципы кодирования чисел в позиционных системах счисления
- чтобы перевести число, скажем, 12345 N , из системы счисления с основанием N в десятичную систему, нужно умножить значение каждой цифры на N в степени, равной ее разряду:
4 3 2 1 0 ← разряды
1 2 3 4 5 N = 1·N 4 + 2·N 3 + 3·N 2 + 4·N 1 + 5·N 0
- последняя цифра записи числа в системе счисления с основанием N – это остаток от деления этого числа на N
- две последние цифры – это остаток от деления на N 2 и т.д.
- число 10 N записывается как единица и N нулей :
- число 10 N записывается как единица и N нулей :
- число 10 N записывается как единица и N нулей :
- число 10 N записывается как единица и N нулей :
- число 10 N записывается как единица и N нулей :
- число 10 N записывается как единица и N нулей :
- число 10 N записывается как единица и N нулей :
- число 10 N записывается как единица и N нулей :
- число 10 N записывается как единица и N нулей :
- число 10 N -1 записывается как N девяток:
- число 10 N -10 M = 10 M · (10 N-M – 1) записывается как N-M девяток, за которыми стоят M нулей:
- число 2 N в двоичной системе записывается как единица и N нулей:
- число 2 N -1 в двоичной системе записывается как N единиц:
число 2 N –2 K при K в двоичной системе записывается как N–K единиц и K нулей :
- число 3 N записывается в троичной системе как единица и N нулей :
- число 3 N-1 записывается в троичной системе как N двоек :
- число 3 N – 3 M = 3 M · (3 N-M – 1) записывается в троичной системе как N-M двоек , за которыми стоят M нулей :
Пример I:
Значение арифметического выражения: 9 8 + 3 5 – 9 записали в системе счисления с основанием 3 . Сколько цифр « 2 » содержится в этой записи?
Решение:
1. приведём все слагаемые к виду 3 N и расставим в порядке убывания степеней:
9 8 + 3 5 – 9 = 3 16 + 3 5 – 3 2
2. первое слагаемое, 3 16 , даёт в троичной записи одну единицу – она нас не интересует
3. пара 3 5 – 3 2 даёт 5 – 2 = 3 двойки
Ответ: 3
Пример II:
Сколько значащих нулей в двоичной записи числа 4 512 + 8 512 – 2 128 – 250
Решение:
1. приведём все числа к степеням двойки, учитывая, что 250 = 256 – 4 – 2 = 2 8 – 2 2 – 2 1 :
(2 2 ) 512 + (2 3 ) 512 – 2 128 – 2 8 + 2 2 + 2 1 =
4 512 + 8 512 – 2 128 – 250 =
= 2 1536 + 2 1024 – 2 128 – 2 8 + 2 2 + 2 1
2. число 2 N –2 K при K записывается как N–K единиц и K нулей:
3. для того чтобы использовать это свойство, нужно представить заданное выражение в виде пар вида 2 N –2 K , причём в этой цепочке степени двойки нужно выстроить по убыванию:
2 1536 + 2 1024 – 2 128 – 2 8 + 2 2 + 2 1
4. Но, два знака «минус» подряд, не позволяет сразу использовать формулу
- используем равенство
- в нашем выражении: – 2 128 = – 2 129 + 2 128
- получаем 2 1536 + ( 2 1024 – 2 129 )+( 2 128 – 2 8 )+ 2 2 + 2 1
- здесь две пары 2 N –2 K , а остальные слагаемые дают по одной единице
- общее число единиц : 1 + (1024 – 129) + (128 – 8) + 1 + 1 = 1018
- количество значащих нулей: 1537 – 1018 = 519
Ответ: 519
Пример III:
Сколько единиц содержится в двоичной записи результата выражения: (2·100 8 ) 500 − 4 501 + 2 502 ?
Решение
(2·100 8 ) 500 − 4 501 + 2 502 = (2 · 8 2 ) 500 − 4 501 + 2 502 =
= (2 · (2 3 ) 2 ) 500 − (2 2 ) 501 + 2 502 = (2 · 2 6 ) 500 − (2 2 ) 501 + 2 502 =
= (2 7 ) 500 − (2 2 ) 501 + 2 502 = 2 3500 − 2 1002 + 2 502
2 n есть двоичное число, в котором имеется одна единица и n нулей после нее.
Тогда:
Рассмотрим операцию вычитания в двоичной системе:
n
m
m
n-1
При таком вычитании из числа с единицей в позиции n числа с единицей в позиции m получается двоичное число, в котором единицы стоят в позициях с ( n – 1 ) по m , после которых записаны только нули .
В нашем случае 2 3500 − 2 1002 дает число, в котором единицы стоят в позициях с 3499 до 1002 .
Рассмотрим операцию сложения в двоичной системе счисления, когда одно число содержит некоторое количество единиц в позициях с ( n – 1) по m , а другое содержит только одну «лидирующую» единицу в позиции, меньшей m , и некоторое количество нулей.
m
n-1
Такое сложение добавляет в получаемое число еще одну единицу в позиции, соответствующей степени двойки в прибавляемом числе.
Тогда в двоичном числе, являющемся результатом вычисления выражения 2 3500 − 2 1002 + 2 502 ,
единицы расположены в позициях с 3499 по 1002 включительно плюс имеется еще одна единица в позиции 502 .
Всего единиц в этом числе: (3499 – 1002 + 1) + 1 = 2499 .
Ответ: 2499
Сколько единиц в двоичной записи числа 4 2015 + 8 405 – 2 150 – 122
Пример IV:
Решение:
1. приведём все числа к степеням двойки, учитывая, что 122 = 128 – 4 – 2 = 2 7 – 2 2 – 2 1 :
4 2015 + 8 405 – 2 150 – 122 = (2 2 ) 2015 + (2 3 ) 405 – 2 150 – 2 7 + 2 2 + 2 1 =
= 2 4030 + 2 1215 – 2 150 – 2 7 + 2 2 + 2 1
2. число 2 N –2 K при K записывается как N–K единиц и K нулей:
3. для того чтобы использовать это свойство, нужно представить заданное выражение в виде пар вида 2 N –2 K , причём в этой цепочке степени двойки нужно выстроить по убыванию:
2 4030 + 2 1215 – 2 150 – 2 7 + 2 2 + 2 1
4. Но, два знака «минус» подряд, не позволяет сразу использовать формулу
- используем равенство
- в нашем выражении: – 2 150 = – 2 1501 + 2 150
- получаем 2 4030 + ( 2 1215 – 2 151 )+( 2 150 – 2 7 )+ 2 2 + 2 1
- здесь две пары 2 N –2 K , а остальные слагаемые дают по одной единице
- общее число единиц : 1 + (1215 – 151) + (150 – 7) + 1 + 1 = 1210
Ответ: 1210
Пример V:
Сколько единиц в двоичной записи числа 4 2014 + 2 2015 – 8
Решение:
1. Приведём все числа к степеням двойки :
4 2014 + 2 2015 – 8 =
(2 2 ) 2014 + 2 2015 – 2 3 =
2 4028 + 2 2015 – 2 3
2. Т.к. число 2 N -1 в двоичной системе записывается как N единиц:
а число 2 N –2 K при K записывается как N–K единиц и K нулей :
3. из п. 2 , число 2 2015 – 2 3 запишется как 2012 единиц и 3 нуля
4. прибавление 2 4028 даст ещё одну единицу , всего получается 2012 + 1 = 2013 единиц
Ответ: 2013
Сколько единиц в двоичной записи числа 4 2016 + 2 2018 – 8 600 + 6
Пример VI:
Решение:
1. Приведём все числа к степеням двойки , разложив 6 как 2 2 +2 1 :
4 2016 +2 2018 –8 600 +6 =
(2 2 ) 2016 + 2 2018 - (2 3 ) 600 + 2 2 + 2 1 =
= 2 4032 + 2 2018 – 2 1800 + 2 2 + 2 1
2. Т.к. число 2 N -1 в двоичной системе записывается как N единиц:
а число 2 N –2 K при K записывается как N–K единиц и K нулей :
3. из п. 2 , число 2 2018 – 2 1800 запишется как 218 единиц и 1800 нулей
4. прибавление 2 4032 даст ещё одну единицу , а прибавление 2 2 +2 1 – еще две, всего получается 218 + 3 = 221 единиц
Ответ: 221
Сколько единиц в двоичной записи числа 4 2016 - 2 2018 + 8 800 - 80
Пример VII:
Решение:
1. Приведём все числа к степеням двойки , разложив 80 как 2 6 +2 4 :
4 2016 -2 2018 +8 800 -80 =
(2 2 ) 2016 - 2 2018 + (2 3 ) 800 - 2 6 - 2 4 =
=2 4032 + 2 2400 - 2 2018 - 2 6 - 2 4
=2 4032 - 2 2018 + 2 2400 - 2 6 - 2 4
2. Т.к. число 2 N -1 в двоичной системе записывается как N единиц:
а число 2 N –2 K при K записывается как N–K единиц и K нулей :
3. из п. 2 , число 2 2400 – 2 2018 запишется как 382 единиц и 2018 нулей
2 4032 + 2 2400 - 2 2018
4. прибавление 2 4032 даст число , в котором 383 единицы и в конце (после последней единицы ) – 2018 нулей :
выделим из этого значения последнюю единицу со следующими 2018 нулями как отдельное слагаемое (число 2 2018 ):
где число K содержит 382 единицы в старших разрядах;
таким образом, интересующее нас число
согласно п. 2, число 2 2018 – 2 6 запишется как 2012 единиц и 6 нулей;
также выделим последнюю единицу с последующими нулями как отдельное слагаемое:
где число L содержит 2011 единиц
теперь остаётся найти, сколько единиц будет в двоичной записи числа 2 6 – 2 4 , согласно п. 2 находим, что оно содержит 2 единицы
общее число единиц равно 382 + 2011 + 2 = 2395
Ответ: 2395
- получаем 2 4030 + ( 2 1215 – 2 151 )+( 2 150 – 2 7 )+ 2 2 + 2 1
- здесь две пары 2 N –2 K , а остальные слагаемые дают по одной единице
- общее число единиц : 1 + (1215 – 151) + (150 – 7) + 1 + 1 = 1210
Ответ: 1210
Пример VIII:
Решите уравнение
Ответ запишите в троичной системе счисления . Основание системы счисления указывать не нужно.
Решение:
1. переведём все числа в десятичную систему счисления:
2. собирая всё в одно уравнение получаем
Ответ: 6
3. это уравнение имеет два решения: 6 и -8
4. переводим ответ в троичную систему:
6 = 2∙3 1 = 20 3 .
Ответ: 20
Пример IX:
Решите уравнение . Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
Решение:
1. переведем все числа в десятичную систему, решим уравнение и результат переведем в шестеричную систему
2. уравнение приобретает вид
откуда получаем
3. переводим 15 в шестеричную систему счисления:
Ответ: 23
Пример X:
Запись десятичного числа в системах счисления с основаниями 3 и 5 в обоих случаях имеет последней цифрой 0 . Какое минимальное натуральное десятичное число удовлетворяет этому требованию?
Решение:
в данной задаче требуется найти наименьшее натуральное число , которое делится одновременно на 3 и на 5 , то есть , делится на 15
Ответ: 15
Пример XI:
Запись числа 67 10 в системе счисления с основанием N оканчивается на 1 и содержит 4 цифры. Укажите основание этой системы счисления N .
Решение:
1. поскольку запись в системе счисления с основанием N заканчивается на 1, то остаток от деления числа 67 на N равен 1 , то есть при некотором целом k имеем
2. следовательно, основание N – это делитель числа 66
3. с другой стороны, запись числа содержит 4 цифры, то есть
4. выпишем кубы и четвертые степени первых натуральных чисел, которые являются делителями числа 66:
5. из этого списка только для числа N = 3 выполняется условие
Ответ: 3
67 10 = 2111 3
Пример XII:
Запись числа 381 10 в системе счисления с основанием N оканчивается на 3 и содержит 3 цифры. Укажите наибольшее возможное основание этой системы счисления N .
Решение:
1. поскольку запись в системе счисления с основанием N заканчивается на 3 , то остаток от деления числа 381 на N равен 3 , то есть при некотором целом k имеем
2. следовательно, основание N – это делитель числа
3. но, так как запись числа содержит 3 цифры, то
дает
4. неравенство
5. неравенство
дает
6. таким образом,
в этом диапазоне делителями числа 378 являются числа
получаем запись числа
- 9 , при
получаем запись числа
- 14 , при
получаем запись числа
- 18 , при
Ответ: 18
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25 , запись которых в системе счисления с основанием четыре оканчивается на 11 ?
Пример XIII:
Решение:
1. переведем 25 в четверичную систему счисления: 25 = 121 4 ,
2. все интересующие числа не больше этого значения
3. из этих чисел выделим только те, которые заканчиваются на 11
это 11 4 = 5 и 111 4 = 21
таких чисел всего два:
Ответ: 5, 21
Пример XIV:
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2 .
Решение:
1. Здесь нужно найти все целые числа N 3 , такие, что остаток от деления 23 на N равен 2, или
где k– целое неотрицательное число (0, 1, 2, …)
2. Из равенства 23=k N+2 получим k N=21
3. задача сводится к тому, чтобы найти все делители числа 21 , которые больше 2
4. есть только три таких делителя: 3, 7, 21
Ответ: 3, 7, 21
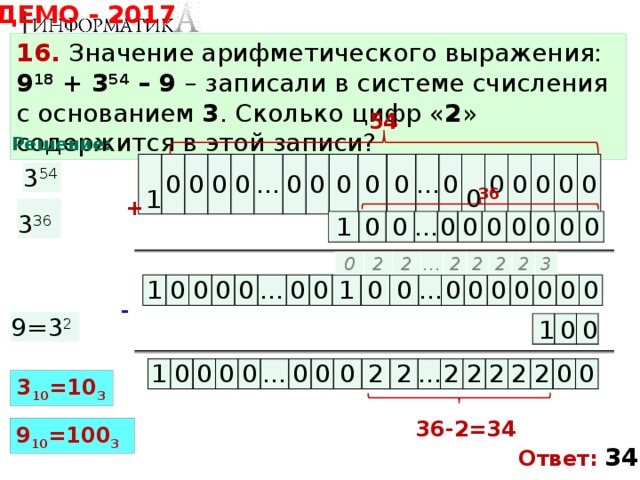
ДЕМО - 2017
16. Значение арифметического выражения: 9 18 + 3 54 – 9 – записали в системе счисления с основанием 3 . Сколько цифр « 2 » содержится в этой записи?
54
Решение:
1
0
0
0
0
…
0
0
0
0
0
…
0
0
0
0
0
0
0
3 54
36
+
3 36
1
0
0
…
0
0
0
0
0
0
0
0
2
2
…
2
2
2
2
3
1
0
0
0
0
…
0
0
1
0
0
…
0
0
0
0
0
0
0
-
9=3 2
1
0
0
1
0
0
0
0
…
0
0
0
2
2
…
2
2
2
2
2
0
0
3 10 =10 3
36-2=34
9 10 =100 3
Ответ: 34
125. Некоторое число X из десятичной системы счисления перевели в системы счисления с основаниями 16 , 8 , 4 , 2 . Часть символов при записи утеряна. Позиции утерянных символов обозначены знаком *:
X = E* 16 = *5* 8 = ***1 4 = *****1** 2
Определите число X .
=224+ *
X = E* 16 =
14 16 1 +* 16 0
224 X
где * может принимать значения
* 8 2 + 5 8 1 + * 8 0 =
* 64+40+ * 1 =
* 65+40+*
X =*5* 8 =
105 X 495
где * может принимать значения от 1 до 7
X = ***1 4 =
* 4 3 + * 4 2 + * 4 1 +1 =
65 X 253
где * может принимать значения от 1 до 3
* 2 7 + * 2 6 + * 2 5 + * 2 4 + * 2 3 +1*2 2 + * 2 1 + * 2 0
X=*****1** 2 =
Где * может принимать значения от 0 до 1
132 X 255
Тогда 224 X 253
Ответ: X= 237
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
