Просмотр содержимого документа
«Высшая математика. вычисление массы материальной кривой»
ББК 22.21
ВЫЧИСЛЕНИЕ МАССЫ МАТЕРИАЛЬНОЙ КРИВОЙ
А.С. Тирский, старший преподаватель кафедры
«Естетственных и технических наук»,
Л.С. Толмачева., студентка группы Мех 09
Олёкминский филиал
ФГБОУ ВПО Якутская ГСХА»,, г. Олёкминск
Как известно, математика все больше и больше внедряет свои методы в технические науки. Целью такого внедрения является оптимизация решения данной задачи. Кроме того, зачастую решить задачу можно только математически. Рассмотрим одну из таких задач механики «Вычисление массы материальной кривой»»
Рассмотрим следующую механическую задачу. Пусть на некоторой плоской спремляемой дуге АВ некоторым образом распределена масса с линейной плотностью  , причем эта плотность задана как непрерывная функция
, причем эта плотность задана как непрерывная функция  от координат х и у точки дуги АВ. Требуется определить массу m материальной дуги кривой.
от координат х и у точки дуги АВ. Требуется определить массу m материальной дуги кривой.
С этой целью разобьем дугу АВ произвольным образом на n частей с помощью точек деления:  , которые пронумерованы от точки А к точке В. Длину дуги
, которые пронумерованы от точки А к точке В. Длину дуги  обозначим через
обозначим через  ). На каждой частичной дуге
). На каждой частичной дуге  возьмем произвольно по точке
возьмем произвольно по точке  и во взятых точках вычислим плотность распределения массы
и во взятых точках вычислим плотность распределения массы  . Если предположить, что плотность во всех точках частичной дуги
. Если предположить, что плотность во всех точках частичной дуги  постоянна и равна ее значению
постоянна и равна ее значению в точке А, то величина массы частичной дуги будет равна
в точке А, то величина массы частичной дуги будет равна  .
.
Так как масса всей дуги АВ равна сумме масс ее частичных дуг, то при сделанном допущении о постоянстве плотности вдоль частичных дуг масса всей дуги выразится суммой:
 (1)
(1)
Поскольку в действительности плотность распределения массы на каждой частичной дуге  , вообще говоря, не постоянна, то сумма (1) не может быть принята за массу дуги АВ. Однако, если частичные дуги малы( точек деления n достаточно много), то в силу непрерывности функции
, вообще говоря, не постоянна, то сумма (1) не может быть принята за массу дуги АВ. Однако, если частичные дуги малы( точек деления n достаточно много), то в силу непрерывности функции  значение плотности в различных точках какой- либо из этих дуг будет весьма мало отличаться от ее значения в точке А и масса (1) будет приближенно выражать массу дуги АВ, причем это приближение будет тем точнее, чем мельче по длине будут частичные дуги (чем на большее число частичных дуг будет разбита кривая АВ) . поэтому за массу дуги АВ можно принять предел суммы (1) , при условии что длина
значение плотности в различных точках какой- либо из этих дуг будет весьма мало отличаться от ее значения в точке А и масса (1) будет приближенно выражать массу дуги АВ, причем это приближение будет тем точнее, чем мельче по длине будут частичные дуги (чем на большее число частичных дуг будет разбита кривая АВ) . поэтому за массу дуги АВ можно принять предел суммы (1) , при условии что длина 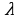 наибольшей частичной дуги стремится к нулю
наибольшей частичной дуги стремится к нулю (
( .
.
 (2)
(2)
Сравнивая последнюю формулу с определением криволинейного интеграла первого рода, получим:
 (3)
(3)
Рассмотрим пример:
Найти массу дуги кривой  между точками А и В, для которых
между точками А и В, для которых  и
и 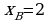 , если в каждой точке дуги АВ линейная плотность пропорциональна квадрату ординаты.
, если в каждой точке дуги АВ линейная плотность пропорциональна квадрату ординаты.
Решение:
Здесь  ,
, 

Применяя формулу (3),получим:
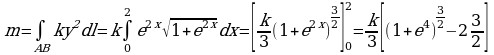
Литература:
Шипачев В.С. Задачник по высшей математике: Учебное пособие для вузов – М. Высшая школа, 2001.- 345с.
Шипачев В.С. Основы высшей математики: Учебное пособие для вузов – М: Высшая школа, 1998.- 380с.
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, в 2-х частях Ч.1,Ч.2.:Учебн. пособие для вузов – М.: Высшая школа, 1999.- 280с.







 , причем эта плотность задана как непрерывная функция
, причем эта плотность задана как непрерывная функция  от координат х и у точки дуги АВ. Требуется определить массу m материальной дуги кривой.
от координат х и у точки дуги АВ. Требуется определить массу m материальной дуги кривой.  , которые пронумерованы от точки А к точке В. Длину дуги
, которые пронумерованы от точки А к точке В. Длину дуги  обозначим через
обозначим через  ). На каждой частичной дуге
). На каждой частичной дуге  и во взятых точках вычислим плотность распределения массы
и во взятых точках вычислим плотность распределения массы  . Если предположить, что плотность во всех точках частичной дуги
. Если предположить, что плотность во всех точках частичной дуги  .
.  (1)
(1)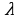 наибольшей частичной дуги стремится к нулю
наибольшей частичной дуги стремится к нулю (
( .
. (2)
(2) (3)
(3) между точками А и В, для которых
между точками А и В, для которых  и
и 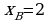 , если в каждой точке дуги АВ линейная плотность пропорциональна квадрату ординаты.
, если в каждой точке дуги АВ линейная плотность пропорциональна квадрату ординаты. ,
,