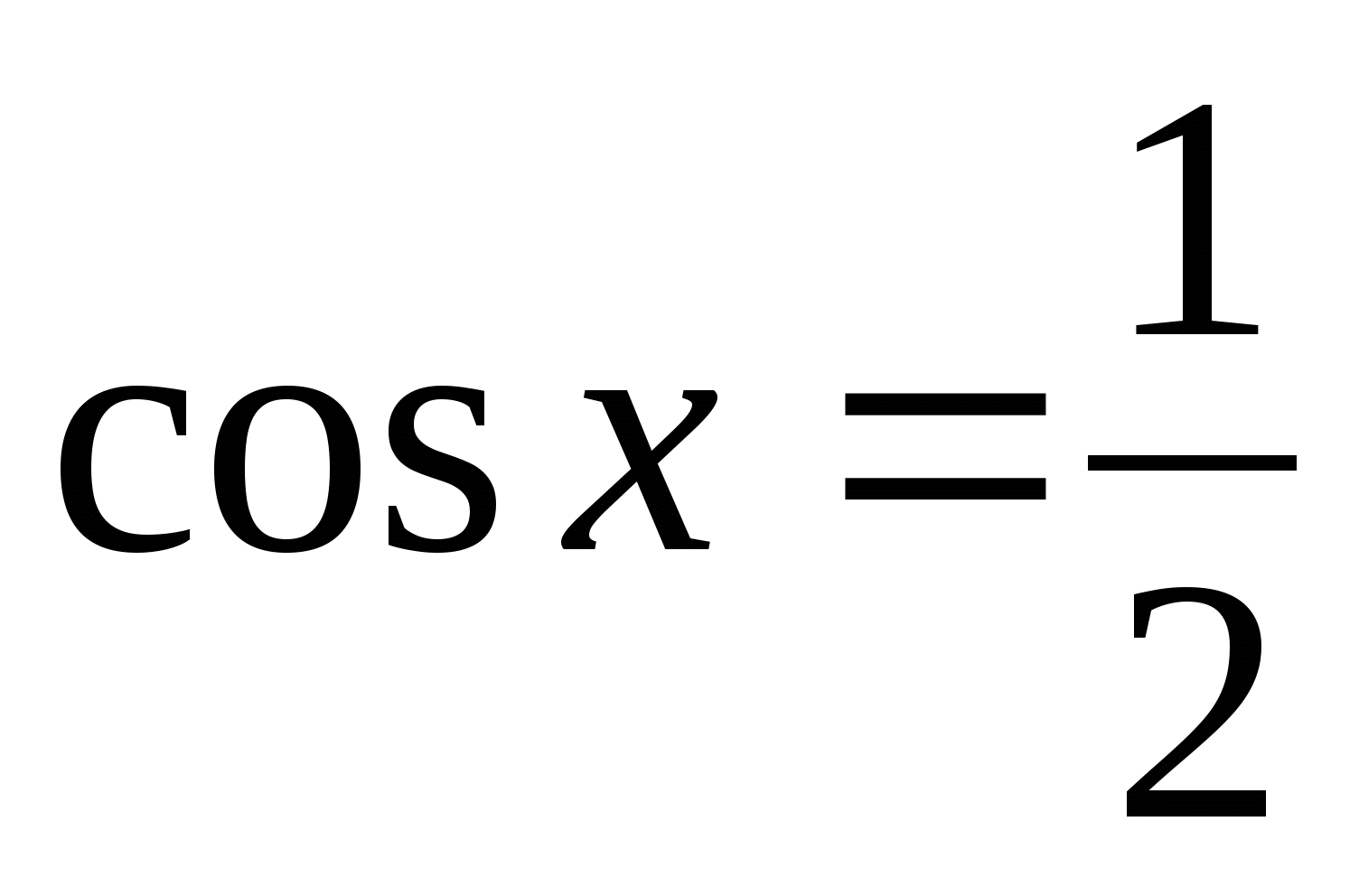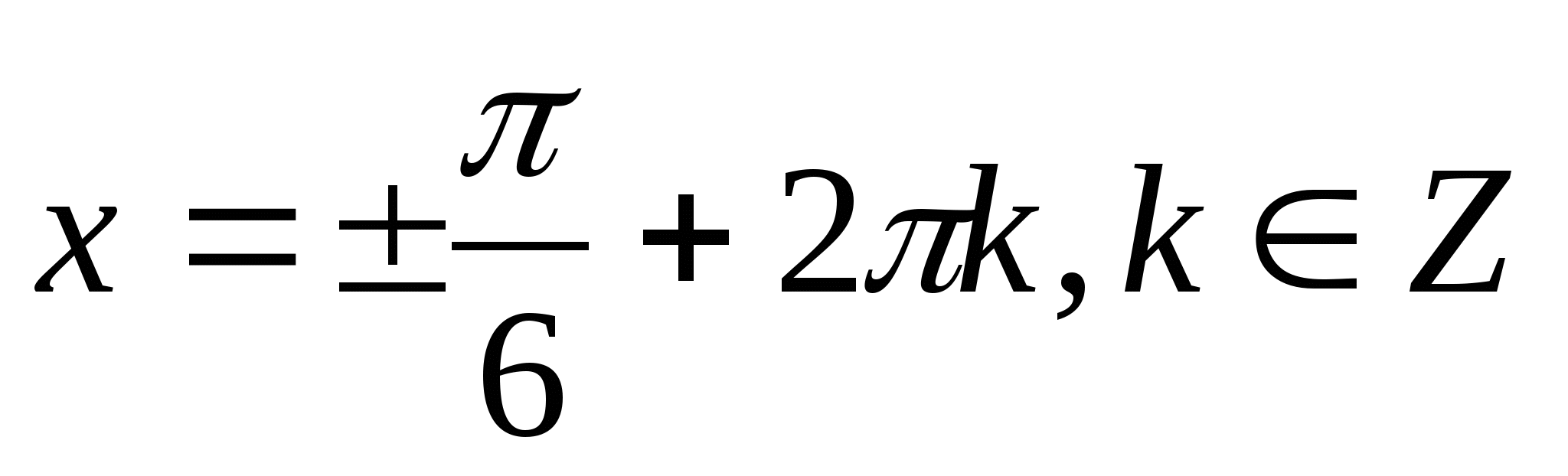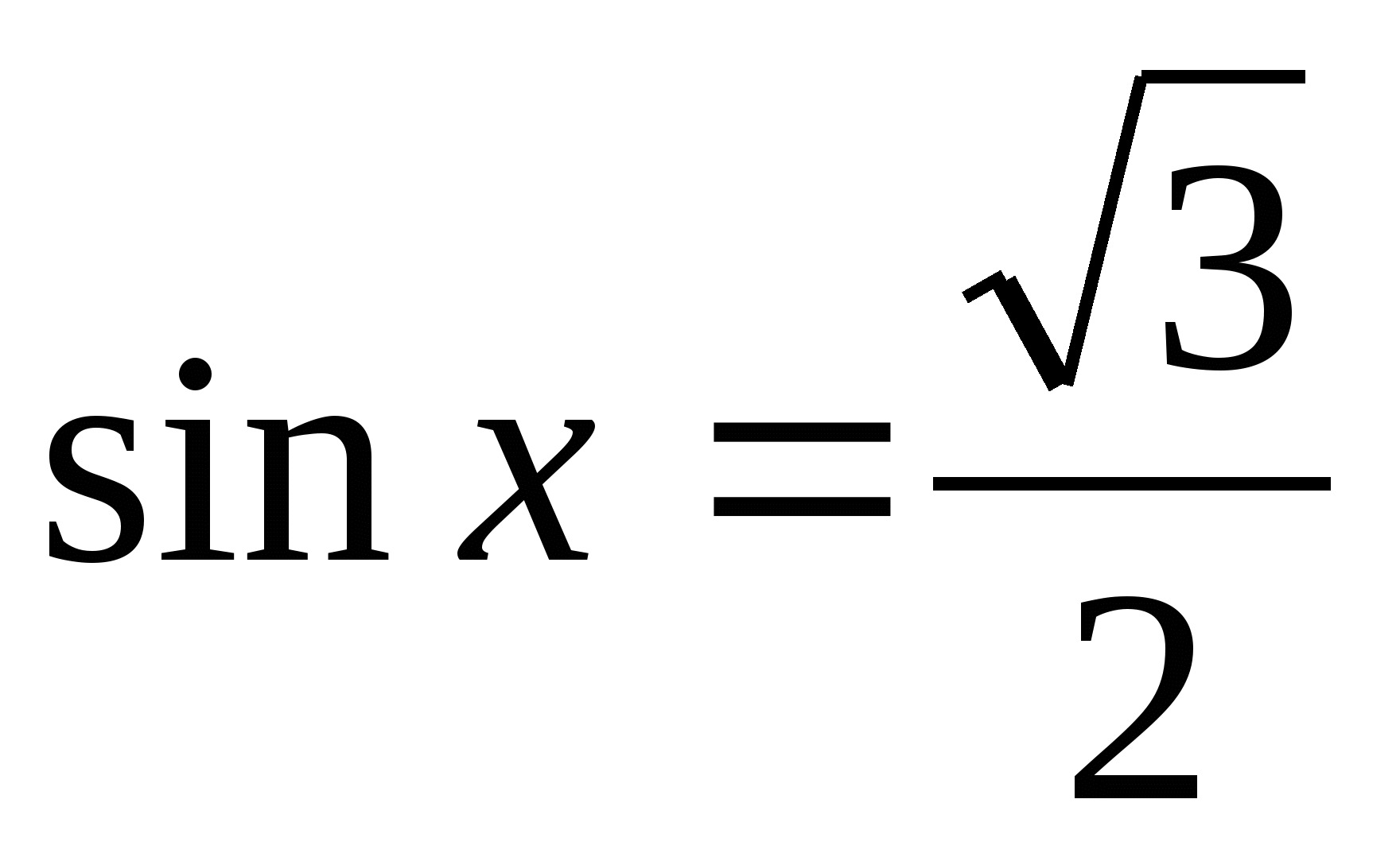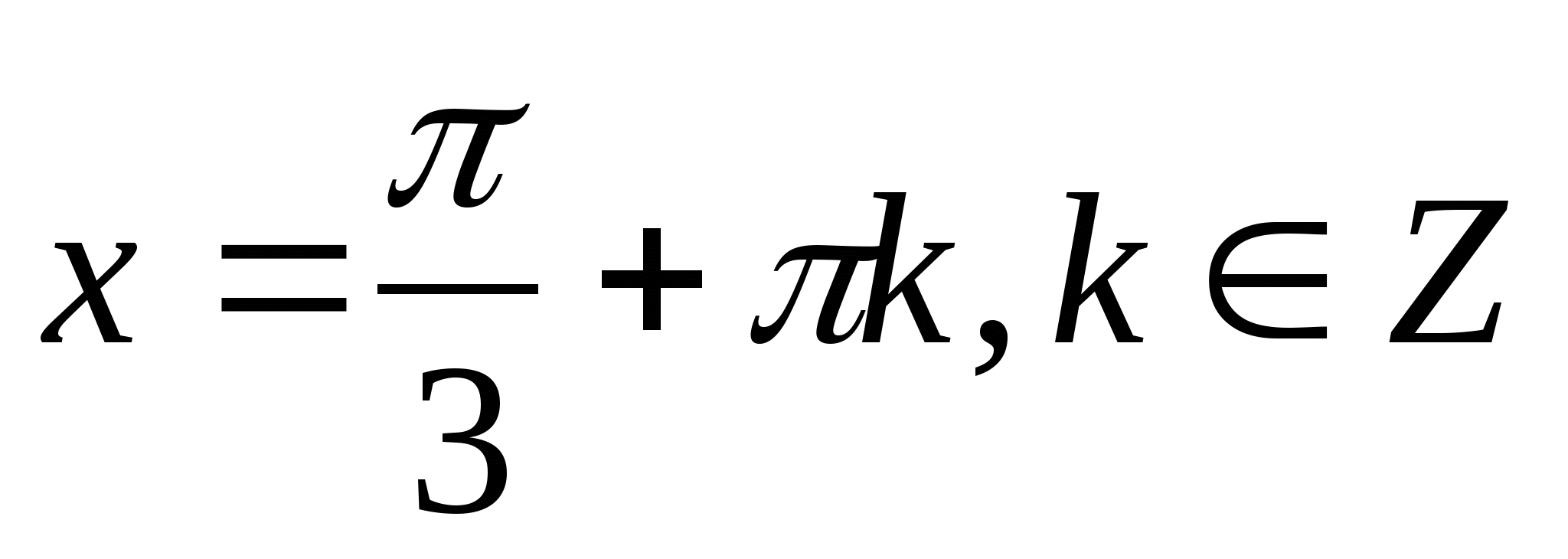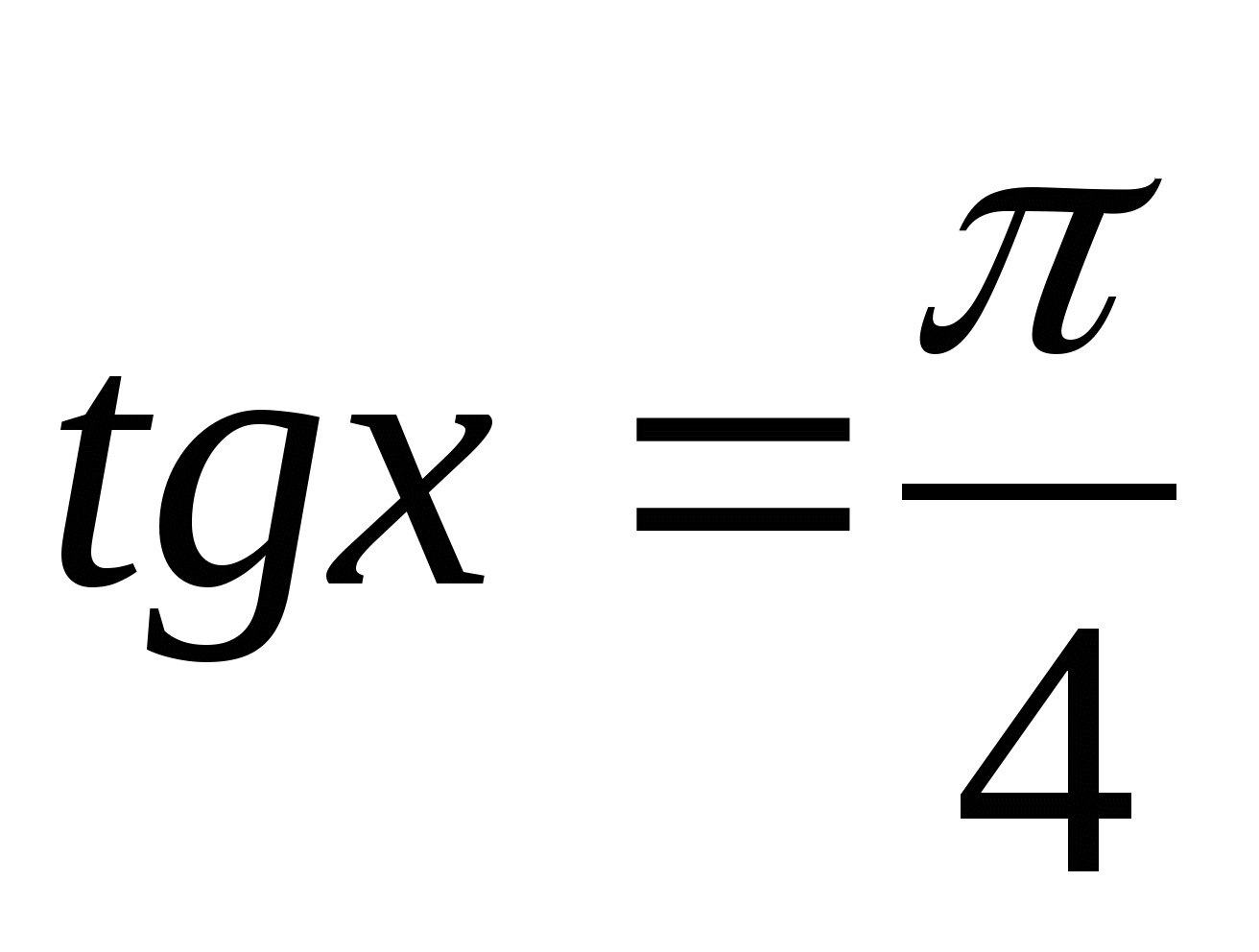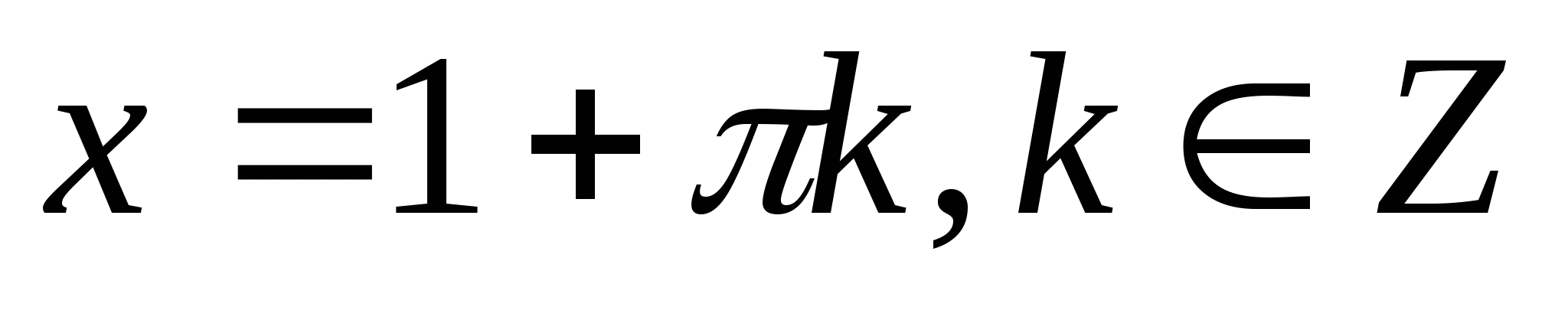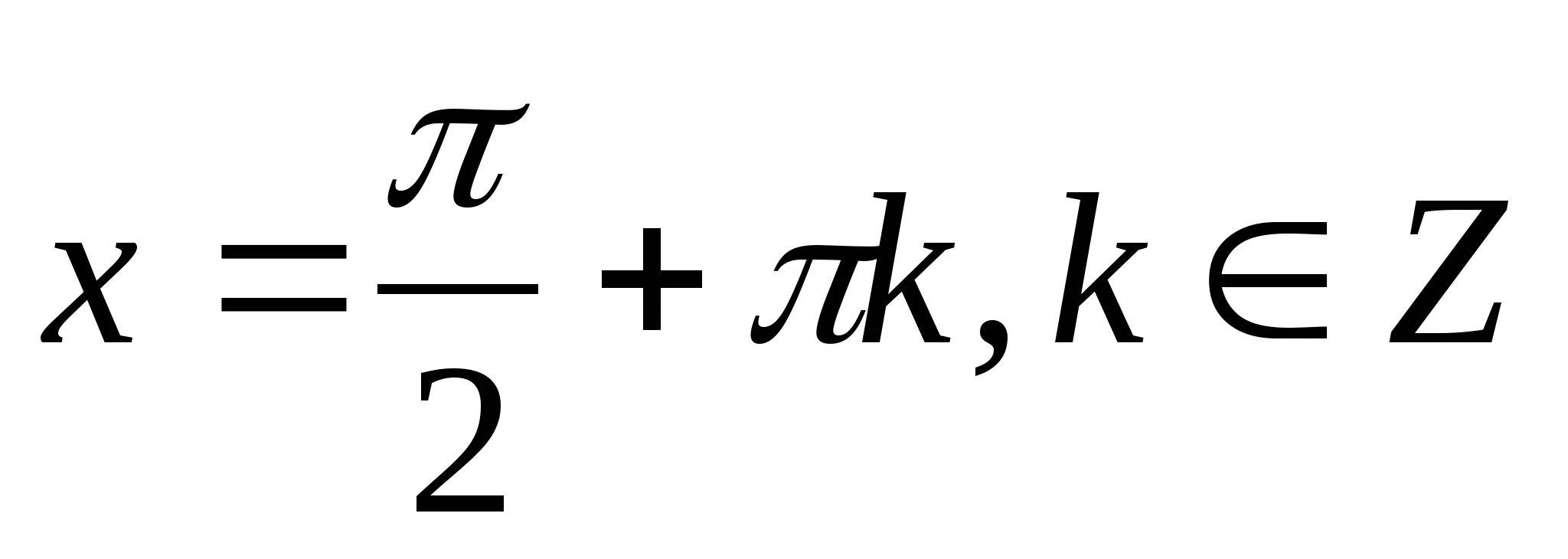Урок математики в 10 классе по теме "Решение тригонометрических уравнений"

Открытый урок по математике в 10 классе

Тема урока: «Решение тригонометрических уравнений».

Тип урока: урок-практикум.

Цели:

Обучающие:

• обобщение и систематизация знаний и способов действий;

• проверка, оценка и коррекция знаний и способов действий;

Развивающие:

• развитие самопроверки, самоконтроля, самостоятельности, внимательности;

• формирование умения выбирать оптимальную стратегию при решении конкретной задачи работы в целом;

• развитие умения аргументировано участвовать в обсуждении решений;

Воспитательные:

• формирование культуры математической речи;

• содействие воспитанию интереса к математике, активности.

К концу занятия обучающиеся смогут:

• анализировать методы решения уравнений;

• применять методы решения уравнений к тригонометрическим уравнениям;

• распознавать методы решения тригонометрических уравнений;

• формулировать алгоритмы решения тригонометрических уравнений в зависимости от метода.

Оборудование:

Экран, проектор, компьютер, ОК по теме, рабочая карточка к уроку, карточка-консультант.

Ход урока:

1. Оргмомент. (Ознакомление с темой, целями и задачами занятия, психологический настрой на деятельность).

Учитель:

Здравствуйте! Внимание! Сегодняшний урок я хочу начать с таких слов. Великий русский физик, математик и политик. А.Эйнштейн заметил: «Мне приходится делить время между политикой и уравнениями. Однако, уравнения гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно». Сегодня на уроке мы повторяем, приводим в систему наши знания по решению тригонометрических уравнений.

• Как вы думаете, а ваша задача какая?

• Что требуется от вас?

• (Ответы обучающихся).

• Правильно. Показать свои знания и умения по решению тригонометрических уравнений.

Мы должны проверить свои умения:

• Решать простейшие тригонометрические уравнения, решать тригонометрические уравнения по заданному алгоритму;

• Решать тригонометрические уравнения, самостоятельно выбирая метод решения;

• Применять полученные знания в нестандартных ситуациях.

Тригонометрия традиционно популярна при проведении всевозможных экзаменов (в том числе ЕГЭ), конкурсов, олимпиад.

В связи с этим очень важно научиться решать тригонометрические уравнения, определять способы решения тригонометрических уравнений.

1. Актуализация знаний и способов действий по теме.

1. Работа в парах над опорным конспектом (самостоятельно). Решение простейших тригонометрических уравнений.

(в это время – работа по карточке у доски: задания из ЕГЭ)

1. Устная работа. Учимся на чужих ошибках. Работа в парах по рабочей карточке. Задание №1 «Найди ошибку». Проверка с места по одному заданию с комментированием. Презентация 1

2. Классификация методов решения тригонометрических уравнений. Презентация 2

(зачитывают обучающиеся)

1. Практическая часть.

1. Распознавание методов, заполнение таблицы.

Работа в парах над заданием №2 по рабочей карточке. Презентация 3

1. Решений некоторых уравнений предыдущего задания с разбором у доски.

2. Решение тригонометрических уравнений из сборника ЕГЭ (проверка работы у доски по карточкам).

1. Итог урока. Обобщающая беседа.

1)Какие типы тригонометрических уравнений вы знаете?

2) Какие методы применяются при решении тригонометрических уравнений?

3) Сформулируйте алгоритм решения тригонометрических уравнений.

К сожалению нельзя указать общего метода решения тригонометрических уравнений, почти каждое из них (кроме простейших) требует особого подхода. Я надеюсь, что сегодняшний урок прошел для вас с пользой. Думаю, научившись бороться с трудностями при решении тригонометрических уравнений, вы сможете преодолевать любые жизненные трудности.

Выставление оценок.

Домашнее задание.

1. Повторить основные формулы решения простейших тригонометрических уравнений, методы решения тригонометрических уравнений.

2. Практическое задание ( 3 уровня сложности ).

Рефлексия.

Закончите предложения:

• Сегодня я понял(а), что мне необходимо…

• При решении тригонометрических уравнений важно…

• Самое трудное для меня…

• Меня удивило…

• Было интересно…

Выполняя устные упражнения, вспоминаем основные формулы решения простейших тригонометрических уравнений.

Найди ошибку:

№1

№2

№3.

№4.

№5

№6.

№7

№8

№9

№10

Определите метод решения тригонометрических уравнений и распределите их в таблицу (в таблицу запиши номер уравнения)

Домашнее задание.

Уровень ниже среднего

Средний уровень

Уровень выше среднего

Способы решения тригонометрических уравнений

Основные типы уравнений и стандартные способы их решения

Содержание

I. Введение

II. Способы решения:

1) Замена переменной

2) Решение однородных уравнений

3) Разложение на множители

4) Решение линейных уравнений

а)введение вспомогательного угла

б)сведение к однородному

5) Решение уравнений, содержащих высокие степени

6) Решение уравнений, c ограниченным ОДЗ

7) Универсальная тригонометрическая подстановка (дополнительно)

I. Введение

перейти

К оглавлению

● При решении тригонометрических уравнений, стараются привести уравнения к уравнению, содержащему одну функцию одного аргумента.

● Способы решения уравнений различны, однако, можно выделить основные типы уравнений и стандартные способы их решений.

II. Способы решения

перейти

Замена переменной

1

К оглавлению

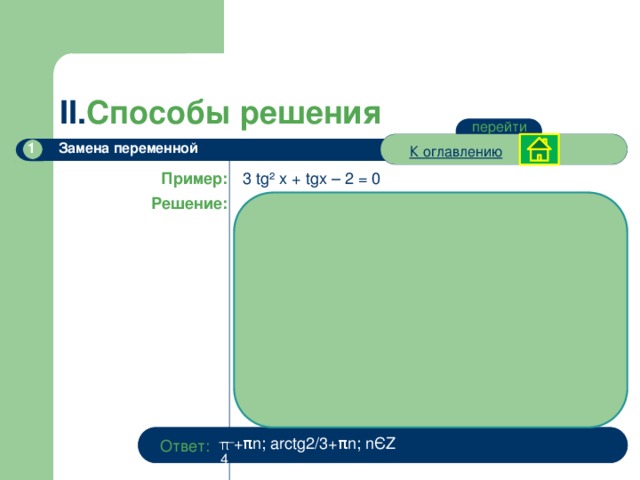
Пример:

3 tg ² x + tgx – 2 = 0

Решение:

t = tg x

3t² + t – 2 = 0

D = 1+4 · 2 · 3=25

t = -1 t = 2/3

-1-5

-1+5

t = или t=

6

6

tgx = -1 tgx = 2/3

x =- + πk; k Є Z

x= arctg2/3+πn; nЄZ

π

4

+ πn; arctg2/3+πn; nЄZ

Ответ:

π

4

II. Способы решения

Решение однородных уравнений (теория)

2

Однородные уравнения относительно sin x и cos x:

a sinx + b cosx = 0

a sin²x + b sinx cosx + c cos²x = 0

Значения х при которых соsх = 0 , не являются решениями уравнения, т.к. если cosx = 0, то sinx = 0, а sinx и cosx не могут быть равными нулю одновременно.

cosx ≠ 0 в однородных уравнениях

II. Способы решения

перейти

Решение однородных уравнений

2

3sinx + 2 cosx = 0

Пример:

// разделим на cosx ≠0 в однородном уравнении

Решение:

3 tgx +2 =0

3tgx = -2

tgx = -2/3

x=arctg(-2/3) + πn, n Є Z

arctg(-2/3) + πn, n Є Z

Ответ:

II. Способы решения

перейти

разложение на множители

3

К оглавлению

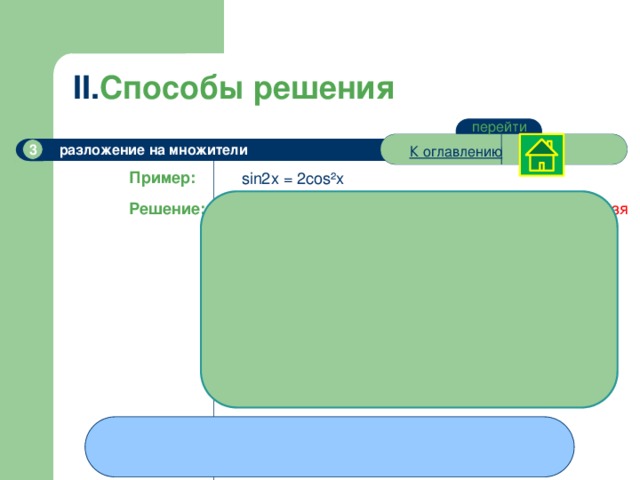
Пример:

sin2x = 2cos²x

Решение:

2 sinx cosx -2 cos²x= 0 ! Делить на cosx нельзя

2cosx (sinx –cosx) = 0

cosx= 0 или sinx – cosx = 0 |разделим на cosx ≠0 в однородном ур-и

x = +πk, k Є Z, или tgx -1=0

x = +πn, n Є Z

π

2

π

4

Ответ:

7

II. Способы решения

4

Линейные уравнения относительно sinx и cosx (теория)

4a

Введение вспомогательного угла

Поделив обе части на получим:

II. Способы решения

4

Линейные уравнения относительно sinx и cosx

4a

Введение вспомогательного угла

Пример:

Решение:

4б

Ответ:

II. Способы решения

перейти

4

Линейные уравнения относительно sinx и cosx

4б

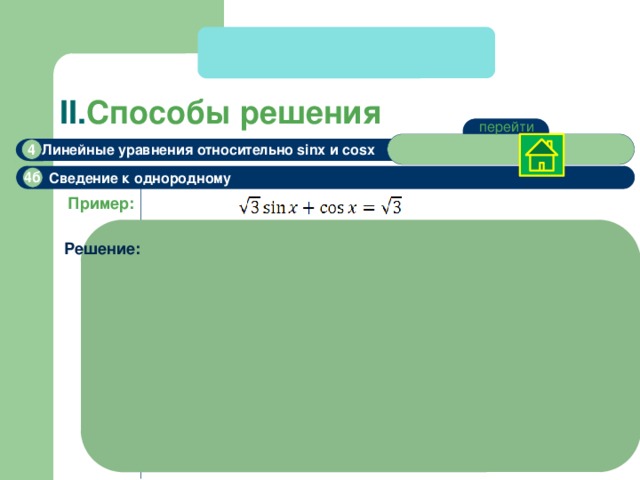
Сведение к однородному

Пример:

Решение:

:

Ответ:

II.Способы решения

5

Решение уравнений, содержащих выс. степени

Формулы понижения степени:

2 cos ²x = 1+ cos2x

2sin²x = 1 – cos2x

2sinx ∙ cosx = sin2x

sin²x +cos²x = 1

(sin²x + cos²x)² = 1

sin ⁴x + cos⁴x =

=sin ⁴ x + 2sin²x cos²x + cos⁴x – 2sin²x cos²x =

= 1 – 2 sin²x cos²x = 1 – 0,5 sin²2x

sin⁶x + cos⁶x =

=(sin²x + cos²x)(sin⁴x + sin²x cos²x + cos⁴x)=

=sin⁴x + 2sin²x cos²x + cos⁴x – 3 sin²x cos²x = 1 – 0,75 · sin²2x

II.Способы решения

перейти

К оглавлению

5

Решение уравнений, содержащих выс. степени

Пример:

4sin ⁴x +12 cos²x = 7

Решение:

(2sin²x)² + 6( 2cos²x) = 7

(1-cos2x)² + 6(1+cos2x)=7

1-2cos2x+cos²2x+6+6cos2x=7

cos²2x + 4cos2x = 0

cos2x(cos2x +4)=0

cos2x=0 или сos2x +4=0

2x = π/2+ πn или т.к. |cos t|

x = π/4+πn/2, n Є Z

+

-

+

-

+

π/4+πn/2, n Є Z

Ответ:

-

II. Способы решения

перейти

К оглавлению

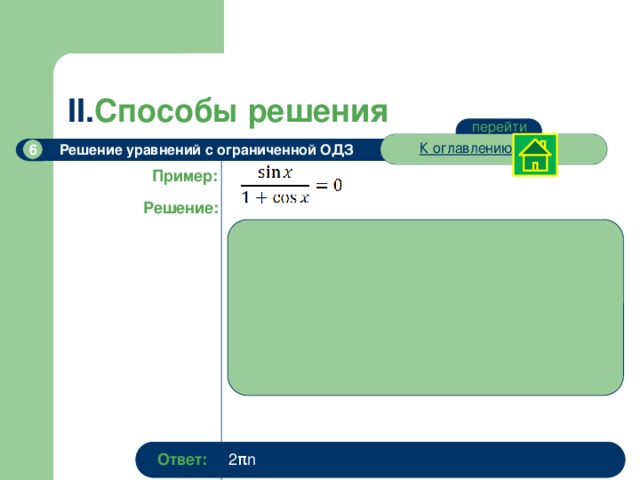
Решение уравнений с ограниченной ОДЗ

6

Пример:

Решение:

Найдем ОДЗ:

cosx ≠-1; x ≠ π +2 πn, n Є Z

sinx=0

x= πn, n Є Z – сравним с ОДЗ

x= 2πn

2πn

Ответ:

II. Универсальная тригонометрическая подстановка

Этот способ решения применяют лишь в том случае, когда не видно других путей решения.

Полученное выражение поделим и умножим на (т.е. умножим на 1)

II. Универсальная тригонометрическая подстановка (продолжение)

II. Способы решения (продолжение)

Полученное выражение поделим и умножим на

=