Уравнения с параметрами

Неизвестные величины принято обозначать последними буквами латинского алфавита (х, у, z ,…) , параметры – первыми буквами (а, b , c , …) .

Уравнением с параметром а называют уравнение вида f ( x , a ) = 0 , которое надо решить относительно х и в котором буквой а обозначено произвольное действительное число .

Решить уравнение с параметром – значит для каждого значения параметра найти множество всех корней данного уравнения или доказать, что корней нет.

Пример 1. Решить уравнение ax = 1 .

Решение.

1. если a ≠ 0 :

0 · x = 1 – не имеет решений ;

2 . если a = 0 :

Пример 2 . Решить уравнение a 2 x – 1 = x + a .

Решение.

a 2 x – 1 = x + a ;

a 2 x – x = a + 1;

x ( a 2 – 1) = a + 1 ;

1 . если a 2 – 1 ≠ 0 , то есть a ≠ ±1 :

2 . если a = 1 , то есть 0 · x = 2 :

уравнение не имеет решений;

3. если a = –1 , то есть 0 · x = 0 :

Решение.

ОДЗ :

х – 4 ≠ 0 ;

х ≠ 4 ;

а ≠ 2 : x = 2a ;

a = 2 : уравнение не имеет решений ;

х – 2а = 0;

х = 2а ;

х ≠ 4 :

2а ≠ 4 ;

а ≠ 2 ;

Ответ: если а ≠ 2, то уравнение имеет единственное решение x = 2a;

если a = 2, то уравнение не имеет решений.

Пример 4 . Решить уравнение |x – a| = 2 .

Решение.

x 1 = a + 2 , x 2 = a – 2 ;

Ответ: x 1 = a + 2 , x 2 = a – 2 .

Пример 5 . Решить уравнение |x| + |x – a| = 0 .

Решение.

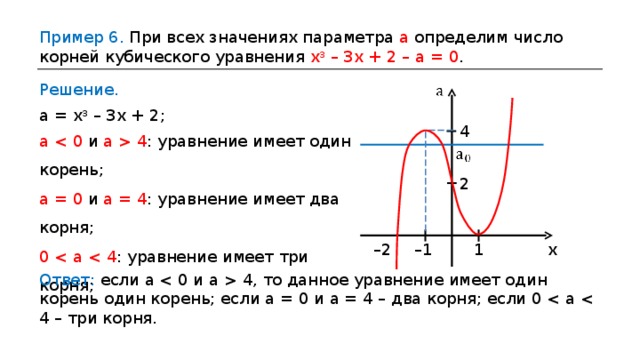
Пример 6. При всех значениях параметра а определим число корней кубического уравнения х 3 – 3х + 2 – а = 0 .

Решение.

а = х 3 – 3х + 2 ;

4

а 4 : уравнение имеет один корень ;

а = 0 и а = 4 : уравнение имеет два корня ;

0

2

– 2

x

– 1

1

Ответ: если а 4, то данное уравнение имеет один корень один корень; если а = 0 и а = 4 – два корня; если 0

Пример 7 . Решить уравнение m х 2 + 3 m х – ( m +2) = 0 .

Решение.

D = m (13 m + 8) ;

D = m (13 m + 8) ≥ 0 ;

Пример 8 . При каких значениях параметра а уравнение

– 2 sin 2 х = (а 2 + 5а + 2) sin х имеет ровно четыре корня на отрезке [0; 2π] ?

Решение.

1

sin х = 0 ;

0

– 1

Ответ: а = – 1, а = – 4, а = 0, а = – 5.