Цикл уроков по теме Стереометрия

СТЕРЕОМЕТРИЯ

Многогранники

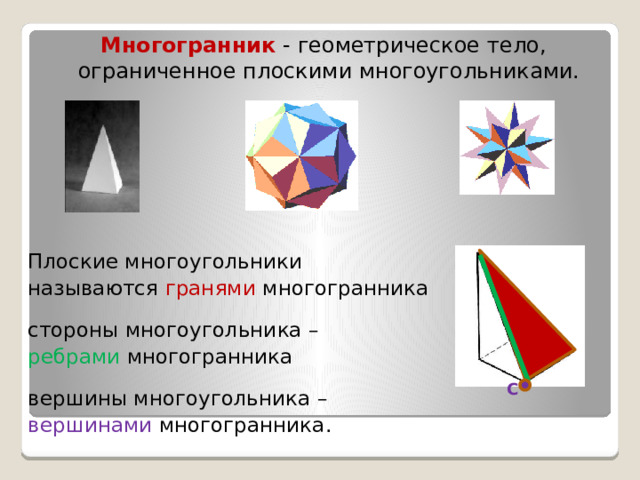
Многогранник - геометрическое тело, ограниченное плоскими многоугольниками.

Плоские многоугольники

называются гранями многогранника

стороны многоугольника –

ребрами многогранника

вершины многоугольника –

вершинами многогранника. 

С

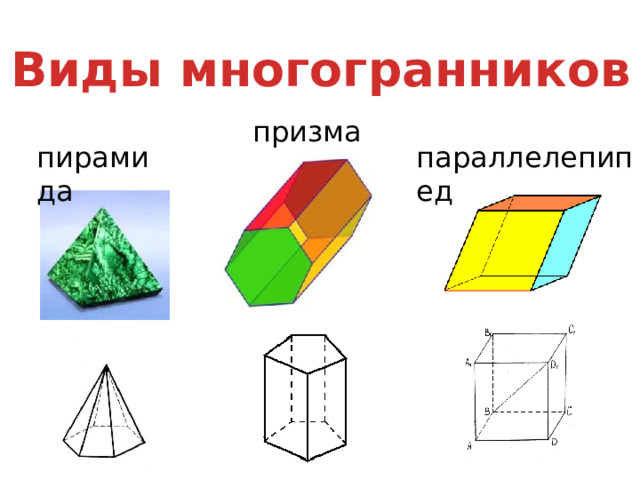
Виды многогранников

призма

пирамида

параллелепипед

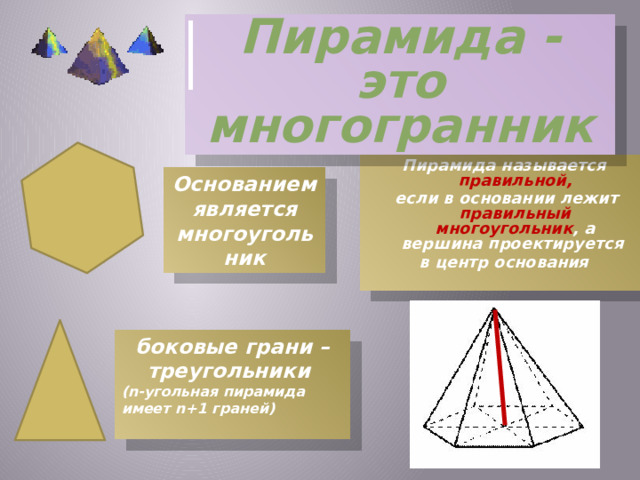
Пирамида - это многогранник

Пирамида называется правильной,

если в основании лежит правильный многоугольник , а вершина проектируется

в центр основания

Основанием является многоугольник

боковые грани – треугольники

(n-угольная пирамида имеет n+1 граней)

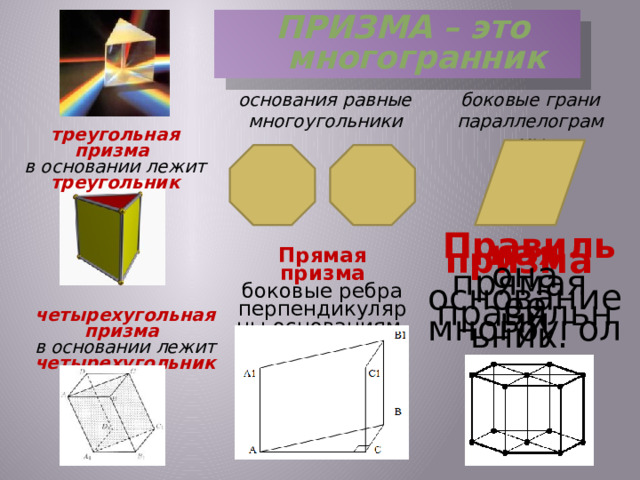
ПРИЗМА – это многогранник

основания равные многоугольники

боковые грани параллелограммы

треугольная призма

в основании лежит треугольник

  Правильная призма

она прямая

основание ее правильный многоугольник. 

Прямая призма боковые ребра перпендикулярны основаниям

четырехугольная призма

в основании лежит четырехугольник

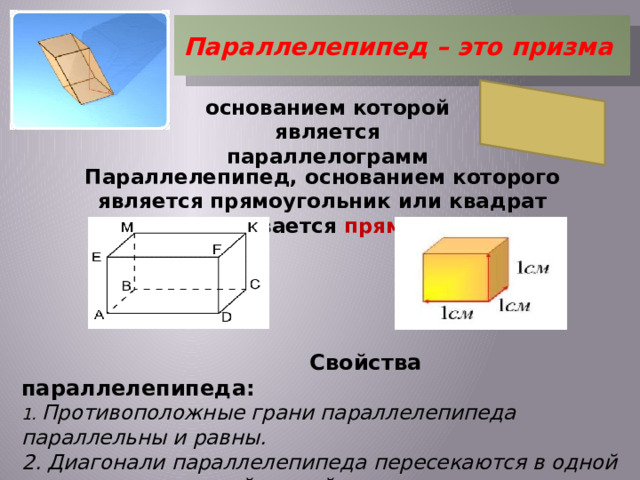
Параллелепипед – это призма

основанием которой является параллелограмм

Параллелепипед, основанием которого является прямоугольник или квадрат называется прямым  

Свойства параллелепипеда: 1. Противоположные грани параллелепипеда параллельны и равны. 2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

Правильные многогранники

Додекаэдр

Тетраэдр

Молодцы!

Октаэдр

Икосаэдр

Куб

Тетраэдр

( от ,,тетра”- четыре и греческого ,,hedra” - грань)

состоит из 4-х правильных треугольников, в каждой его вершине сходятся 3 ребра.

Тетраэдр символизировал огонь,

т.к. его вершина устремлена вверх

тетраэдр-огонь

Гексаэдр (куб)

( от греческого ,,гекса” - шесть и ,,hedra” - грань) имеет 6 квадратных граней, в каждой его вершине сходятся 3 ребра.

Гексаэдр больше известен как куб (от латинского ,,cubus”; от греческого ,,kubos”.

Гексаэдр (куб) символизировал землю,

так как самый «устойчивый»

гексаэдр (куб) - земля

Октаэдр

(от греческого okto - восемь и hedra - грань)

имеет 8 граней (треугольных),

в каждой вершине сходятся 4 ребра.

Октаэдр символизировал воздух,

как самый "воздушный"

октаэдр-воздух

Икосаэдр

(от греческого eikosi - двадцать и hedra - грань)

имеет 20 граней (треугольных),

в каждой вершине сходится 5 рёбер

Икосаэдр символизировал воду,

так как он самый «обтекаемый»

икосаэдр-вода

Додекаэдр

(от греческого dodeka - двенадцать и hedra - грань) имеет 12 граней (пятиугольных),

в каждой вершине сходятся 3 ребра.

Додекаэдр воплощал в себе "все сущее", символизировал все мироздание, считался главным

додекаэдр-вселенная

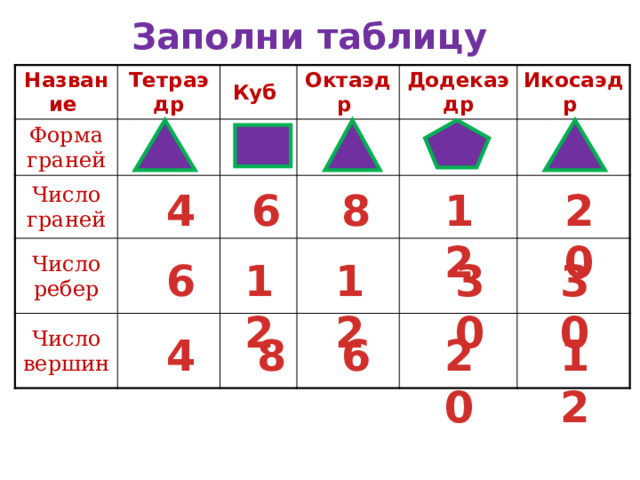
Заполни таблицу

Название

Тетраэдр

Форма граней

Куб

Число граней

Октаэдр

Число ребер

Додекаэдр

Число вершин

Икосаэдр

12

4

20

6

8

30

12

12

30

6

8

6

12

20

4

Число вершин, рёбер и граней правильных многогранников связано друг с другом интересным соотношением.

Теорема Эйлера:

Число вершин - число ребер + число граней =2

Леонард Эйлер

(1707-1783)

Швейцарский, немецкий и российский   математик  

автор более чем 800 работ по математическому анализу, дифференциальной геометрии, теории музыки и др.

Математика  - гимнастика для ума, СТЕРЕОМЕТРИЯ - витамин для мозга.

Многогранники в архитектуре.

Великая пирамида в Гизе

Галикарнасский мавзолей

Никольский собор

Александрийский маяк

Мечеть

Кул-Шариф

Башня Сююмбике

Многогранники в жизни

Понятие цилиндра

Цилиндры вокруг нас.

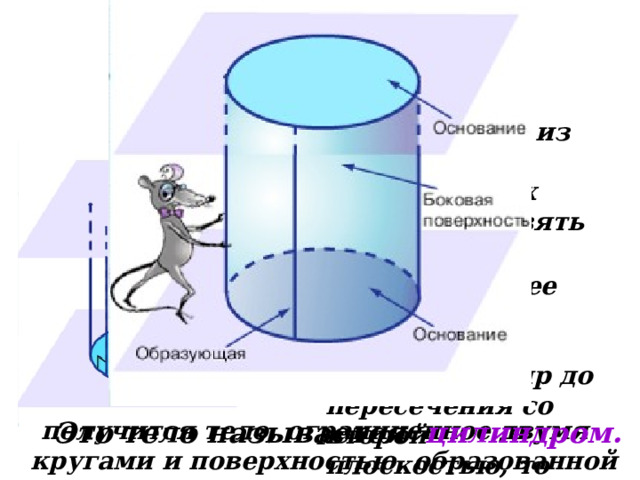
Цилиндрическая поверхность.

Если в одной из двух параллельных плоскостей взять окружность,

и из каждой ее точки восстановить перпендикуляр до пересечения со второй плоскостью, то

получится тело, ограниченное двумя кругами и поверхностью, образованной из перпендикуляров.

Это тело называется цилиндром.

Точное название определенного выше тела – прямой круговой цилиндр.

Вообще, цилиндр возникает при пересечении цилиндрической поверхности, образованной множеством параллельных прямых, проведенных через каждую точку замкнутой кривой линии, и двух параллельных плоскостей.

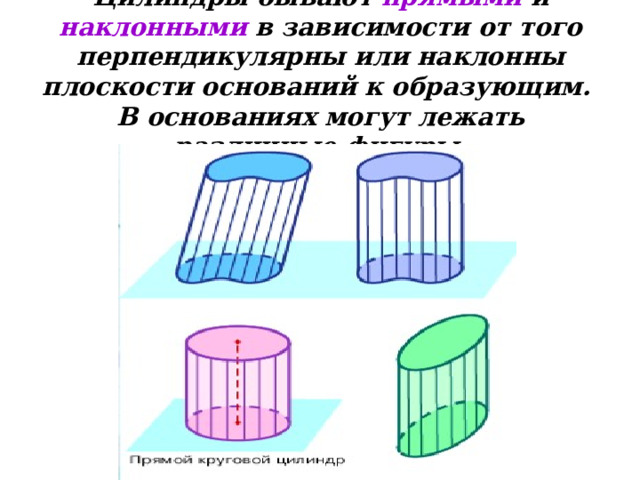
Цилиндры бывают прямыми и наклонными в зависимости от того перпендикулярны или наклонны плоскости оснований к образующим. В основаниях могут лежать различные фигуры.

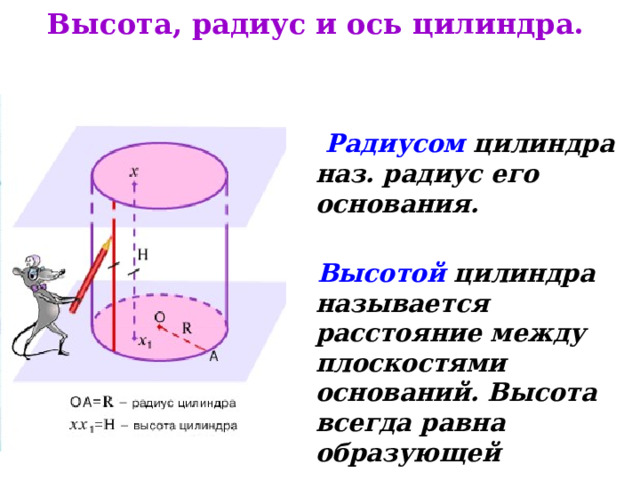
Высота, радиус и ось цилиндра.

Радиусом цилиндра наз. радиус его основания.

Высотой цилиндра называется расстояние между плоскостями оснований. Высота всегда равна образующей

Вспомните формулу нахождения площади круга и найдите площадь основания цилиндра , радиус которого равен 2.

4

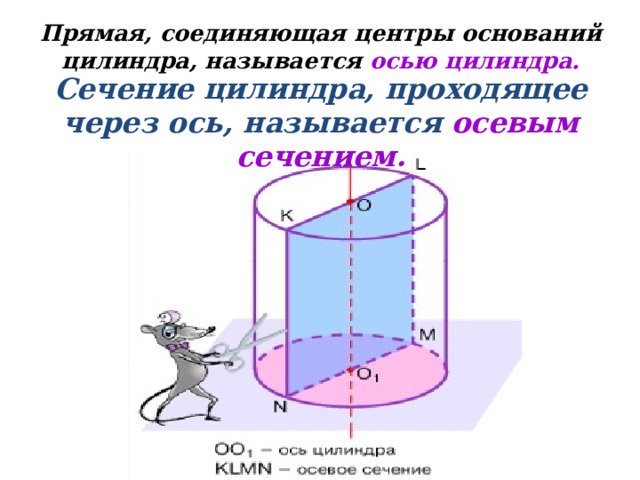
Прямая, соединяющая центры оснований цилиндра, называется осью цилиндра.

Сечение цилиндра, проходящее через ось, называется осевым сечением.

Найдите площадь осевого сечения цилиндра, если известны радиус его основания и высота.

20

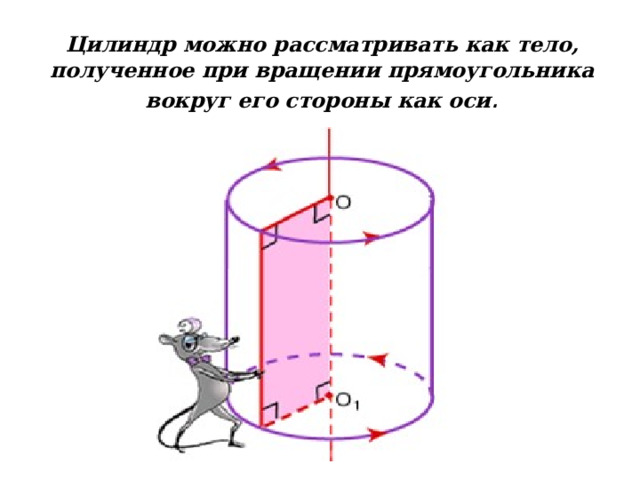
Цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг его стороны как оси .

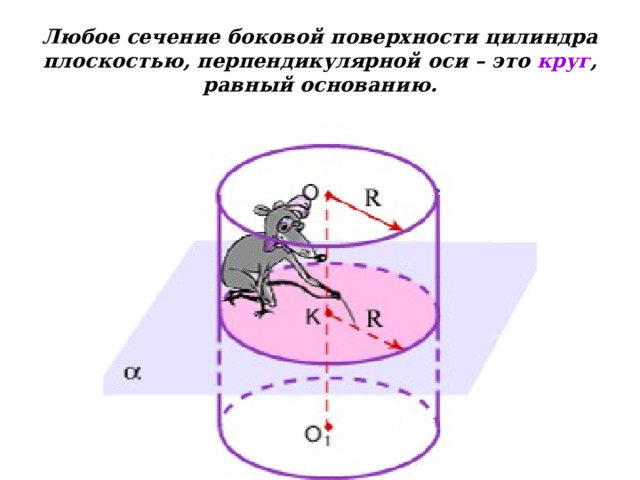
Любое сечение боковой поверхности цилиндра плоскостью, перпендикулярной оси – это круг , равный основанию.

Пусть цилиндр пересекли плоскостью, перпендикулярной оси и получили круг площадью 3 π. Чему равен радиус цилиндра?

Задача.

Высота цилиндра 7 см, а радиус основания 5 см. В цилиндре расположена трапеция так, что все ее вершины находятся на окружностях оснований цилиндра. Найти площадь трапеции и угол между основанием и плоскостью трапеции, если параллельные стороны трапеции равны 6см и 8 см.

Дано: цилиндр; Н = 7, R = 5

АВСD – трапеция,

АВ = 6, СD = 8

Найти: S ABCD ; угол между АВСD и основанием.

Проведем дополнительное построение: построим высоту трапеции, ее проекцию на верхнее основание цилиндра и перенесем параллельным переносом нижнее основание трапеции на верхнее основание цилиндра.

НК – высота трапеции

НН 1 – проекция НК на основание

Н 1 К = ОО 1 = 7

С 1 D 1 | | СD; С 1 D 1 = CD

Рассмотрим проекцию высоты трапеции на верхнее основание цилиндра.

ΔАОВ и ΔС 1 ОD 1 –

равнобедренные.

АН = НВ → НВ = ½ АВ = 3.

С 1 Н 1 =Н 1 D 1 →Н 1 D 1 = ½С 1 D 1 =4

Из ΔОВН: ОН = 4.

Из ΔОD 1 Н 1 : ОН 1 = 3.

7

НН 1 = ОН + ОН 1 =

Найдем высоту трапеции, ее площадь и искомый угол.

НН 1 = 7, Н 1 К = 7

ے Н 1 НК = ے НКН 1 = 45 0

НК = 7√2

S ABCD = ½ (АВ + СD)*НК

S АВСD = 49√2

Задача для самостоятельного решения.

Расстояние от центра верхнего основания до плоскости нижнего основания равно 6, а площадь осевого сечения равна 72. Найдите расстояние от этого центра до хорды нижнего основания, стягивающей дугу в 90 0 .

н 1

О 1 Н 1 = 3 √2

Определение конуса

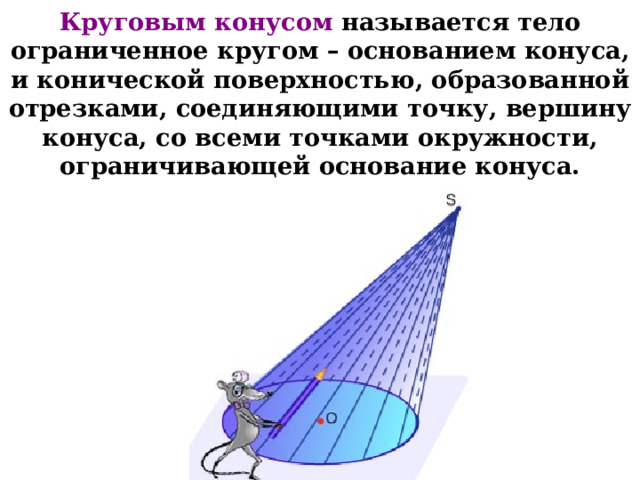
Круговым конусом называется тело ограниченное кругом – основанием конуса, и конической поверхностью, образованной отрезками, соединяющими точку, вершину конуса, со всеми точками окружности, ограничивающей основание конуса.

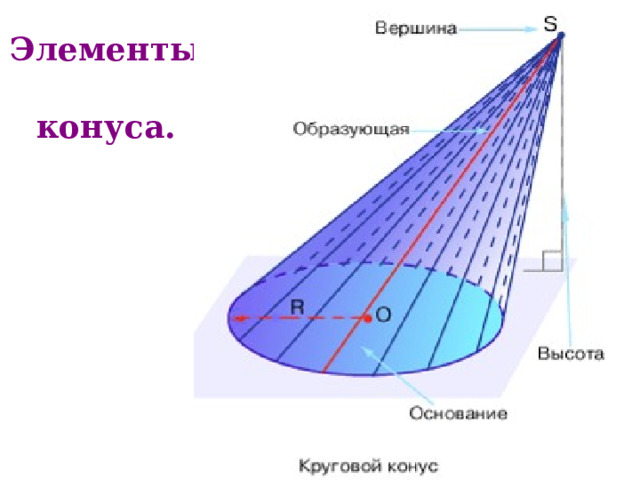
Элементы конуса.

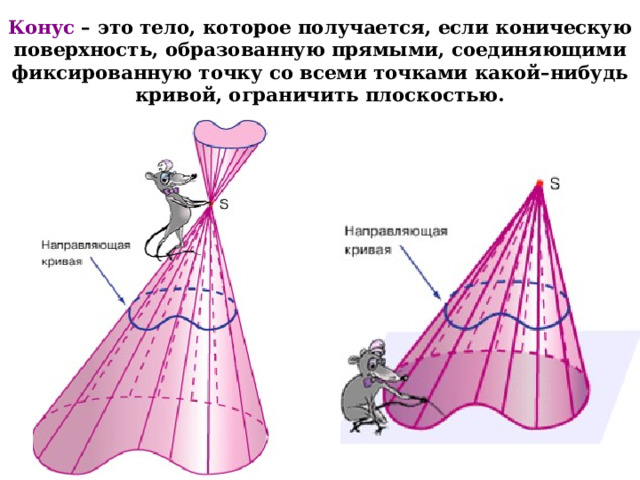
Конус – это тело, которое получается, если коническую поверхность, образованную прямыми, соединяющими фиксированную точку со всеми точками какой–нибудь кривой, ограничить плоскостью.

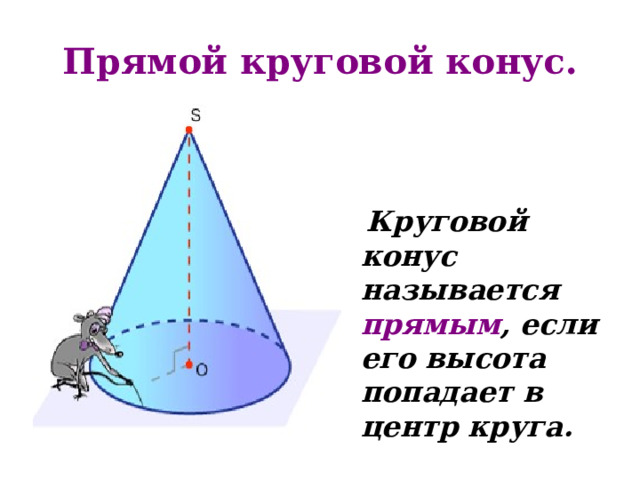
Прямой круговой конус.

Круговой конус называется прямым , если его высота попадает в центр круга.

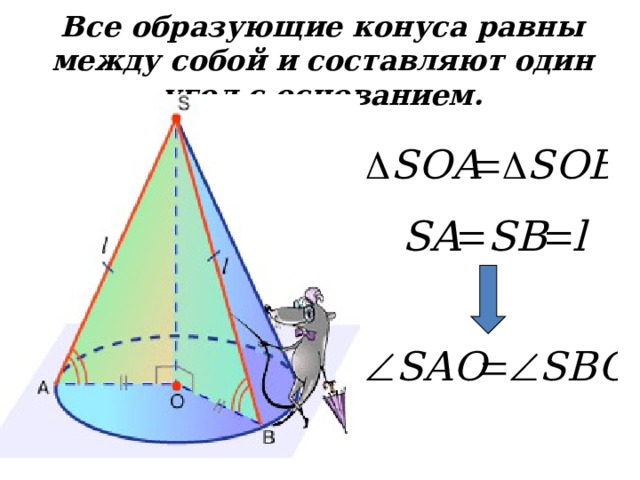
Все образующие конуса равны между собой и составляют один угол с основанием.

?

• Чему равен угол между образующей и основанием конуса, если известен угол между высотой и образующей.

65 0

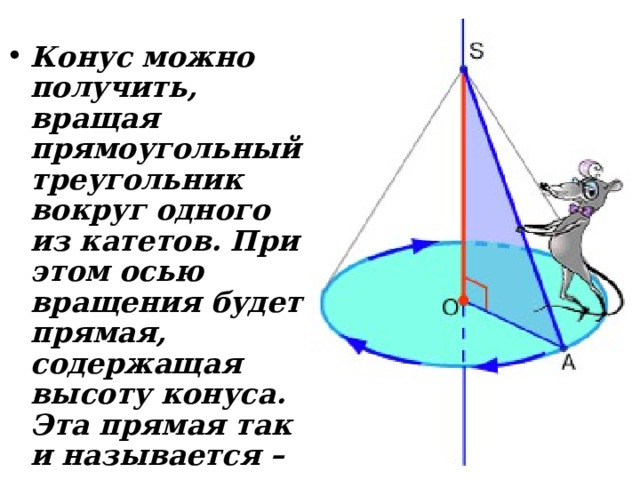
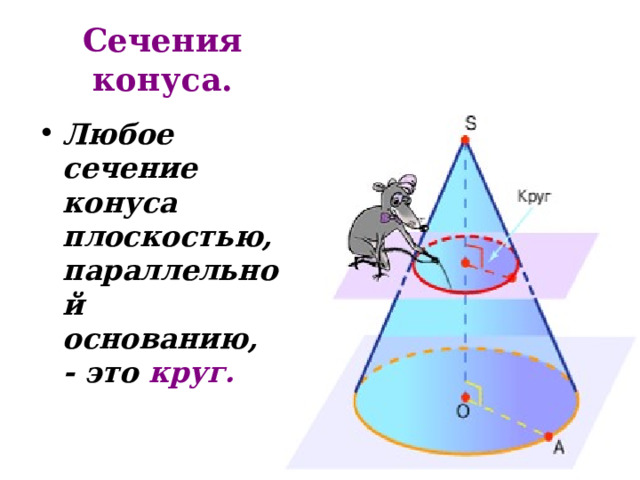
• Конус можно получить, вращая прямоугольный треугольник вокруг одного из катетов. При этом осью вращения будет прямая, содержащая высоту конуса. Эта прямая так и называется – осью конуса.

?

7

• Конус получен при вращении прямоугольного треугольника

S = 14. Радиус основания конуса равен 4. Определите высоту этого конуса.

Сечения конуса.

• Если через вершину конуса провести плоскость, пересекающую основание, то в сечении получится равнобедренный треугольник.

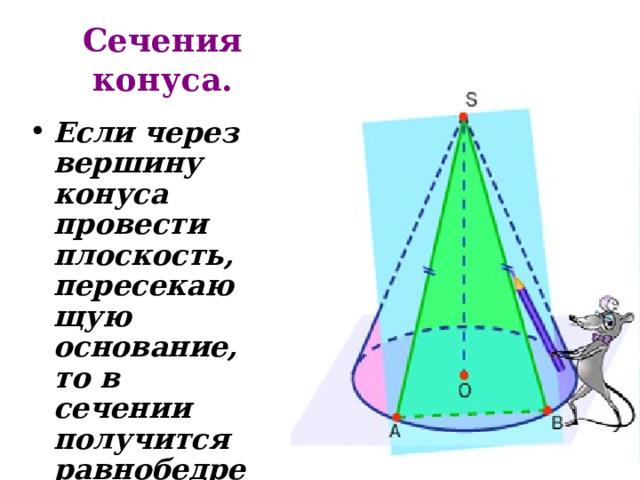
Сечения конуса.

• Сечение конуса, проходящее через ось, называется осевым . В основании осевого сечения лежит диаметр – максимальная хорда, поэтому угол при вершине осевого сечения – это максимальный угол между образующими конуса. ( Угол при вершине конуса ).

?

30

• Найдите площадь осевого сечения, если известны радиус основания конуса и образующая.

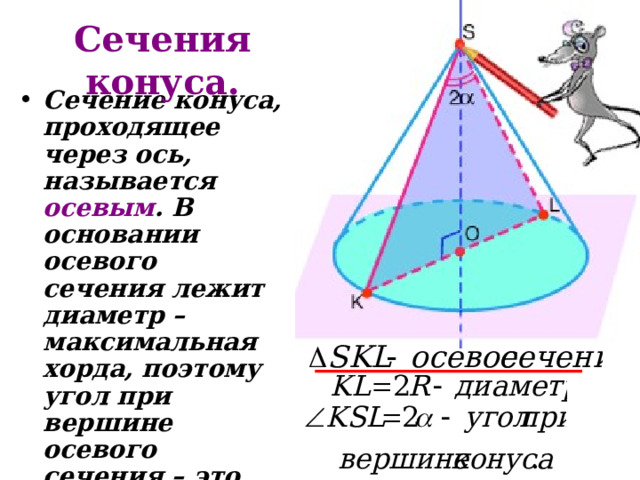
Сечения конуса.

• Любое сечение конуса плоскостью, параллельной основанию, - это круг.

?

• Через середину высоты конуса провели плоскость, перпендикулярную оси, и получили круг R = 5. Чему равна площадь основания конуса?

100 π

Задача.

Дано: H = R = 5;

SAB – сечение;

d (O, SAB) = 3.

Найти: S ΔSAB

1) В сечении равнобедренный треугольник. Найдем его высоту.

~

2) Определим боковые стороны и основание треугольника, являющегося сечением.

3) Вычислим площадь треугольника.

Вписанная и описанная пирамиды.

Пирамидой, вписанной в конус , называется такая пирамида, основание которой – многоугольник, вписанный в основание конуса, а вершина совпадает с вершиной конуса.

?

5 √3

• Пусть высота конуса равна 5 , а радиус основания – 2.

В конус вписана правильная треугольная пирамида. Определите ее объем.

Вписанная и описанная пирамиды.

Пирамида называется описанной около конуса , если ее основание – это многоугольник, описанный около основания конуса, а вершина совпадает с вершиной конуса.

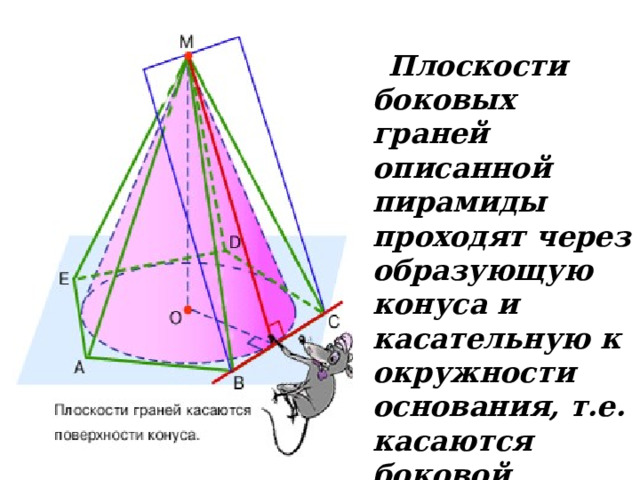
Плоскости боковых граней описанной пирамиды проходят через образующую конуса и касательную к окружности основания, т.е. касаются боковой поверхности конуса.

?

• Вокруг конуса описана правильная четырехугольная пирамида. Радиус основания и образующая конуса известны. Найдите боковое ребро пирамиды.

2√2

Боковая поверхность конуса.

Под боковой поверхностью конуса мы будем понимать предел, к которому стремится боковая поверхность вписанной в этот конус правильной пирамиды, когда число боковых граней неограниченно увеличивается.

Теорема. Площадь боковой поверхности конуса равна половине произведения длины окружности основания на образующую.

Дано:

R – радиус основания конуса,

l – образующая конуса.

Доказать:

S бок.кон. = π Rl

Доказательство:

?

20 π

• Пусть конус будет получен от вращения прямоугольного треугольника с известными катетами. Найдите боковую поверхность этого конуса.

Развертка конуса.

Развертка конуса – это круговой сектор. Его можно рассматривать как развертку боковой поверхности вписанной правильной пирамиды, у которой число боковых граней бесконечно увеличивается.

• Зная угол, образованный высотой и образующей конуса, можно вычислить угол сектора, полученного при развертке конуса, и наоборот.

• Найдем выражение для градусной меры угла развертки конуса.

?

• По данным рисунка определите, чему равен угол развертки этого конуса. Ответ дайте в градусах.

72 0

Задача.

Дано: полукруг радиусом R = 8.

Найти: Н, β ( угол между образующей и основанием.)

1) Используем формулу, связывающую угол кругового сектора развертки с углом между высотой и образующей конуса. Получим угол между высотой и образующей, а затем найдем угол между образующей и основанием конуса.

2) Найдем высоту конуса, используя определение тангенса угла в прямоугольном треугольнике.

Объем конуса.

Теорема. Объем конуса равен одной трети произведения площади основания на высоту.

Дано: R – радиус основания

Н – высота конуса

Доказать: V кон. = 1/3 S осн. H

Доказательство:

Объемом конуса будем считать предел, к которому стремится объем вписанной в этот конус правильной пирамиды, когда число боковых граней неограниченно увеличивается.

Доказательство:

?

12 π

• Найдите объем конуса, если радиус его основания равен трем, а образующая равна пяти.

Задача.

Дано:

SABC – пирамида, вписанная в конус

SA = 13, AB = 5,

ے ACB = 30 0 .

Найти: V конуса

1) Найдем радиус конуса по теореме синусов.

2) У пирамиды, вписанной в конус, высота равна высоте конуса и попадает в центр описанной окружности. Найдем высоту пирамиды.

3) Определим объем конуса.

Сфера и шар

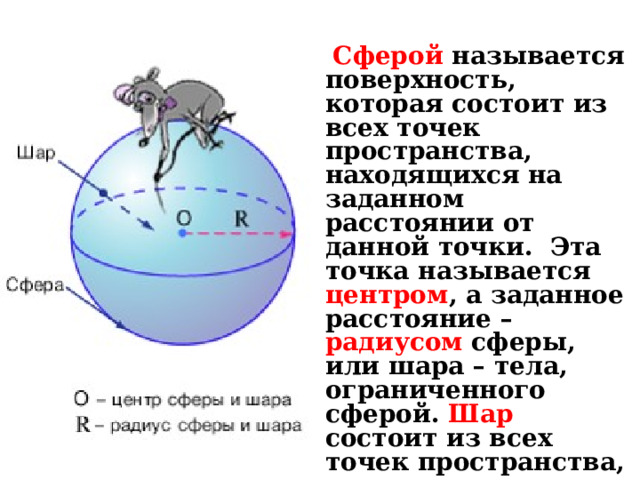
Сферой называется поверхность, которая состоит из всех точек пространства, находящихся на заданном расстоянии от данной точки. Эта точка называется центром , а заданное расстояние – радиусом сферы, или шара – тела, ограниченного сферой. Шар состоит из всех точек пространства, находящихся на расстоянии не более заданного от данной точки.

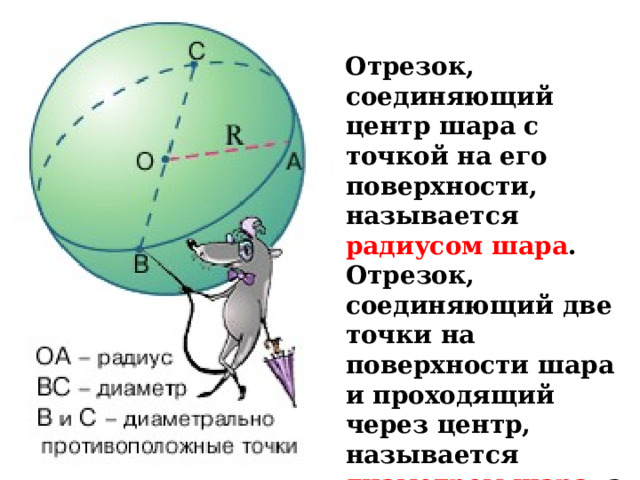
Отрезок, соединяющий центр шара с точкой на его поверхности, называется радиусом шара . Отрезок, соединяющий две точки на поверхности шара и проходящий через центр, называется диаметром шара , а концы этого отрезка – диаметрально противоположными точками шара .

?

18

Чему равно расстояние между диаметрально противоположными точками шара, если известна удаленность точки, лежащей на поверхности шара от центра?

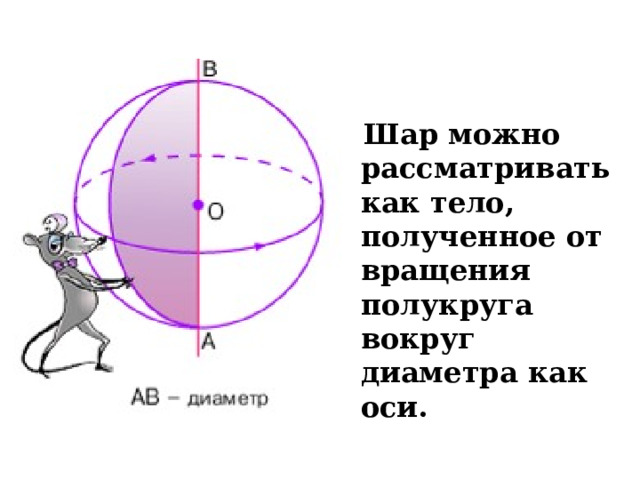
Шар можно рассматривать как тело, полученное от вращения полукруга вокруг диаметра как оси.

?

Пусть известна площадь полукруга. Найдите радиус шара, который получается вращением этого полукруга вокруг диаметра.

4

Теорема . Любое сечение шара плоскостью есть круг. Перпендикуляр, опущенный из центра шара на секущую плоскость, попадает в центр этого круга.

Дано:

Доказать:

Доказательство:

Рассмотрим прямоугольный треугольник, вершинами которого являются центр шара, основание перпендикуляра, опущенного из центра на плоскость, и произвольная точка сечения.

Следствие . Если известны радиус шара и расстояние от центра шара до плоскости сечения, то радиус сечения вычисляется по теореме Пифагора.

10

?

Пусть известны диаметр шара и расстояние от центра шара до секущей плоскости. Найдите радиус круга, получившегося сечения.

Чем меньше расстояние от центра шара до плоскости, тем больше радиус сечения.

?

В шаре радиуса пять проведен диаметр и два сечения, перпендикулярных этому диаметру. Одно из сечений находится на расстоянии три от центра шара, а второе – на таком же расстоянии от ближайшего конца диаметра. Отметьте то сечение, радиус которого больше.

На сфере радиуса R взяты три точки, являющиеся вершинами правильного треугольника со стороной а . На каком расстоянии от центра сферы расположена плоскость, проходящая через эти три точки?

Задача.

Дано:

Найти:

Решение:

Рассмотрим пирамиду с вершиной в центре шара и основанием – данным треугольником.

Решение:

Найдем радиус описанной окружности, а затем рассмотрим один из треугольников, образованных радиусом, боковым ребром пирамиды и высотой,. Найдем высоту по теореме Пифагора.

Наибольший радиус сечения получается, когда плоскость проходит через центр шара. Круг, получаемый в этом случае, называется большим кругом . Большой круг делит шар на два полушара .

?

В шаре, радиус которого известен, проведены два больших круга. Какова длина их общего отрезка?

12

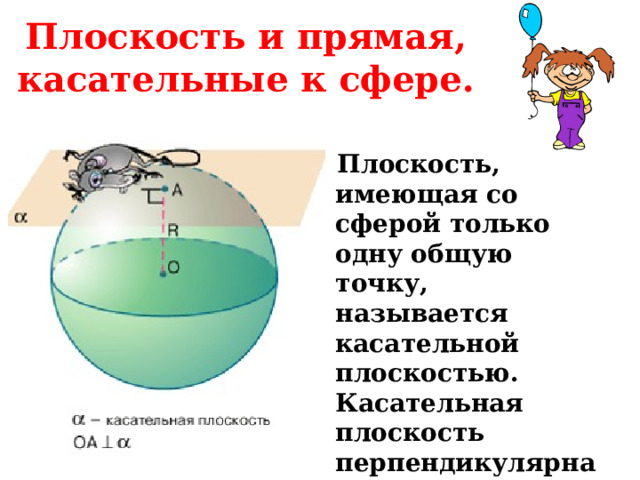
Плоскость и прямая, касательные к сфере.

Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью. Касательная плоскость перпендикулярна радиусу, проведенному в точку касания.

?

Пусть шар, радиус которого известен, лежит на горизонтальной плоскости. В этой плоскости через точку касания и точку В проведен отрезок, длина которого известна. Чему равно расстояние от центра шара до противоположного конца отрезка?

6

Прямая называется касательной , если она имеет со сферой ровно одну общую точку. Такая прямая перпендикулярна радиусу, проведенному в точку касания. Через любую точку сферы можно провести бесчисленное множество касательных прямых.

?

Дан шар, радиус которого известен. Вне шара взята точка, и через нее проведена касательная к шару. Длина отрезка касательной от точки вне шара до точки касания также известна. На каком расстоянии от центра шара расположена внешняя точка?

4

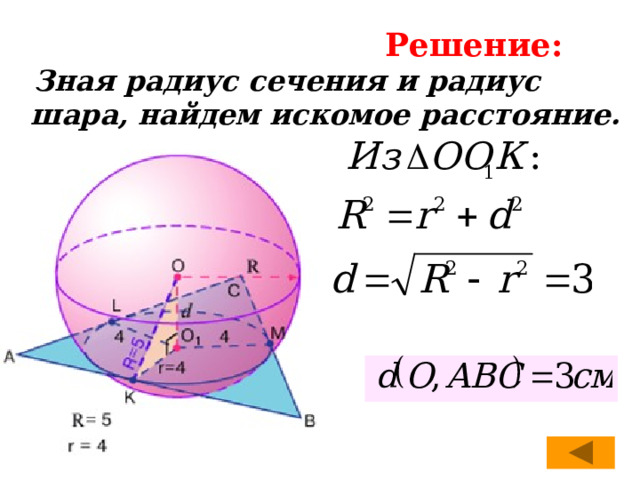
Стороны треугольника 13см, 14см и 15см. Найти расстояние от плоскости треугольника до центра шара, касающегося сторон треугольника. Радиус шара равен 5 см.

Задача.

Дано:

Найти:

Решение:

Сечение сферы, проходящее через точки касания, - это вписанная в треугольник АВС окружность.

Решение:

Вычислим радиус окружности, вписанной в треугольник.

Решение:

Зная радиус сечения и радиус шара, найдем искомое расстояние.

?

π

Через точку на сфере, радиус которой задан, проведен большой круг и сечение, пересекающее плоскость большого круга под углом шестьдесят градусов. Найдите площадь сечения.

Взаимное расположение двух шаров.

Если два шара или сферы имеют только одну общую точку, то говорят, что они касаются. Их общая касательная плоскость перпендикулярна линии центров (прямой, соединяющей центры обоих шаров).

Касание шаров может быть внутренним и внешним.

?

Расстояние между центрами двух касающихся шаров равно пяти, а радиус одного из шаров равен трем. Найдите те значения, которые может принимать радиус второго шара.

2

8

Две сферы пересекаются по окружности . Линия центров перпендикулярна плоскости этой окружности и проходит через ее центр.

?

3

Две сферы одного радиуса, равного пяти, пересекаются, а их центры находятся на расстоянии восьми. Найдите радиус окружности, по которой сферы пересекаются. Для этого необходимо рассмотреть сечение, проходящее через центры сфер.

Вписанная и описанная сферы.

Сфера (шар) называется описанной около многогранника, если все вершины многогранника лежат на сфере.

?

Какой четырехугольник может лежать в основании пирамиды, вписанной в сферу?

Сфера называется вписанной в многогранник, в частности, в пирамиду, если она касается всех граней этого многогранника (пирамиды).

В основании треугольной пирамиды лежит равнобедренный треугольник, основание и боковые стороны известны. Все боковые ребра пирамиды равны 13. Найти радиусы описанного и вписанного шаров.

Задача.

Дано:

Найти:

Решение:

I этап. Нахождение радиуса вписанного шара.

1) Центр описанного шара удален от всех вершин пирамиды на одинаковое расстояние, равное радиусу шара, и в частности, от вершин треугольника АВС. Поэтому он лежит на перпендикуляре к плоскости основания этого треугольника, который восстановлен из центра описанной окружности. В данном случае этот перпендикуляр совпадает с высотой пирамиды, поскольку ее боковые ребра равны.

Решение:

2) Вычислим радиус описанной около основания окружности.

Решение:

3) Найдем высоту пирамиды.

Решение:

4) Радиус описанного шара найдем из треугольника, образованного радиусом шара и частью высоты, прилежащей к основанию пирамиды.

Решение:

II этап. Нахождение радиуса вписанного шара.

Соединим центр вписанного шара со всеми вершинами пирамиды, тем самым мы разделим ее на несколько меньших пирамид. В данном случае их четыре. Высоты всех пирамид одинаковы и равны радиусу вписанного шара, а основания – это грани исходной пирамиды.

Решение:

1) Найдем площадь каждой грани пирамиды и ее полную поверхность.

Решение:

2) Вычислим объем пирамиды и радиус вписанного шара.

Второй способ вычисления радиуса вписанной сферы основан на том, что центр шара, вписанного в двугранный угол, равноудален от его сторон, и, следовательно, лежит на биссекторной плоскости.

Сторона основания правильной четырехугольной пирамиды равна 6, а угол между основанием и боковой гранью равен 60 0 . Определить радиус вписанной сферы.

Задача.

Дано:

Найти:

Решение:

Проведем сечение через вершину пирамиды и середины двух противоположных сторон основания.

• Отрезок, соединяющий центр сферы с серединой стороны основания, делит пополам двугранный угол при основании.

Решение:

Рассмотрим треугольник, полученный в сечении, и найдем искомый радиус из тригонометрических соотношений.