5-мавзу. Тескари матрица. Тескари матрицани ҳисоблаш усуллари.
Reja
Qoʻshma matritsa tushunchasi.
Teskari matritsa ta’rifi. Xos va xosmas matritsalar.
Teskari matritsa mavjudligining zaruriy va etarli sharti.
Ekvivalent almashtirishlar yordamida teskari matritsani hisoblash.
Tayanch soʻz va iboralar. matritsa, qoʻshma matritsa, teskari matritsa, xos va xosmas matritsalar, teskari matritsani hisoblash usullari.
1.Qoʻshma matritsa tushunchasi.
1-ta’rif. 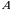 kvadrat matritsaning har bir
kvadrat matritsaning har bir  elementini unga mos algebraik toʻldiruvchisi bilan almashtirish natijasida hosil qilingan matritsa ustida transponirlash amalini bajarishdan hosil boʻlgan
elementini unga mos algebraik toʻldiruvchisi bilan almashtirish natijasida hosil qilingan matritsa ustida transponirlash amalini bajarishdan hosil boʻlgan  matritsa berilgan matritsaga qoʻshma matritsa deyiladi.
matritsa berilgan matritsaga qoʻshma matritsa deyiladi.
Masalan,

matritsaga qoʻshma matritsa

koʻrinishda boʻladi.
1-misol. Quyidagi 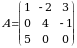 matritsa uchun qoʻshma matritsa topilsin.
matritsa uchun qoʻshma matritsa topilsin.
Yechish. Matritsaning barcha elementlariga mos algebraik toʻldiruvchilarni hisoblaymiz:
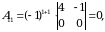

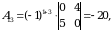
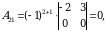

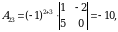
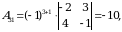
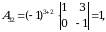
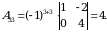
Shunday qilib, berilgan 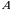 kvadrat matritsaga qoʻshma boʻlgan
kvadrat matritsaga qoʻshma boʻlgan  matritsa
matritsa

koʻrinishda aniqlanadi.
2.Teskari matritsa ta’rifi. Xos va xosmas matritsalar. Teskari matritsa mavjudligining zaruriy va etarli sharti.
2-ta’rif. Agar  kvadrat matritsaning determinanti noldan farqli bo‘lsa, ya’ni
kvadrat matritsaning determinanti noldan farqli bo‘lsa, ya’ni  bo‘lsa,
bo‘lsa,  matritsa xosmas matritsa deyiladi.
matritsa xosmas matritsa deyiladi.
3-ta’rif. Agar  bo‘lsa,
bo‘lsa,  matritsa xos matritsa deyiladi.
matritsa xos matritsa deyiladi.
4-ta’rif. Agar  kvadrat matritsa uchun
kvadrat matritsa uchun 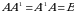 tenglik bajarilsa, u holda
tenglik bajarilsa, u holda 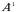 matritsa
matritsa 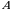 matritsaga teskari matritsa deyiladi.
matritsaga teskari matritsa deyiladi.
1-teorema.  kvadrat matritsaga teskari matritsa mavjud bo‘lishi uchun
kvadrat matritsaga teskari matritsa mavjud bo‘lishi uchun  matritsa xosmas matritsa bo‘lishi zarur va etarli.
matritsa xosmas matritsa bo‘lishi zarur va etarli.
Isbot. Zaruriyligi: Faraz qilaylik  matritsa uchun
matritsa uchun 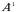 teskari matritsa mavjud bolsin, u holda determinantning xossasiga ko‘ra,
teskari matritsa mavjud bolsin, u holda determinantning xossasiga ko‘ra, 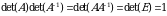 boʻladi. Bundan, agar teskari matritsa mavjud boʻlsa
boʻladi. Bundan, agar teskari matritsa mavjud boʻlsa 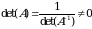 ekanligini kelib chiqadi.
ekanligini kelib chiqadi.
Etarliligi: Faraz qilaylik A n tartibli kvadrat matritsa bo‘lib,  bo‘lsin..
bo‘lsin.. 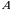 matritsaga qo‘shma
matritsaga qo‘shma  matritsani quramiz
matritsani quramiz

 va
va 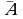 matritsalar ko‘paytmasini qaraymiz:
matritsalar ko‘paytmasini qaraymiz:
 .
.
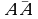 ko‘paytmaning har bir elementi
ko‘paytmaning har bir elementi

yigindidan iborat bo‘ladi. U holda Laplas teoremasi va uning natijasiga ga ko‘ra
 ,
,
Qaysiki, bu yerda
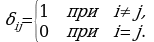
Bundan  va
va 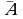 matritsalar ko‘paytmasi, quyidagi skalyar matritsaga teng boladi.
matritsalar ko‘paytmasi, quyidagi skalyar matritsaga teng boladi.
 .
.
Bundan,
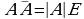 . (*)
. (*)
Xuddi shu usulda
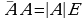 (**)
(**)
Tenglikni keltirib chiqarish mumkin. U holda (*) va (**) tengliklardan
 ,
,
yoki
 (***)
(***)
Kelib chiqadi. Haqiqatan ham (*) dan
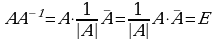 ,
,
va (**) dan bu qurilgan 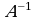 matritsa
matritsa  matritsaga teskari matritsa bo‘ladi, ya’ni
matritsaga teskari matritsa bo‘ladi, ya’ni
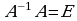 .
.
Teorema isbotlandi.
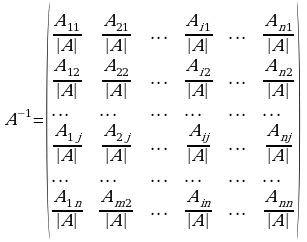
Yuqoridagi (***) tenglik teskari matritsani hisoblash qoidasini beradi.
Izoh. Teskari matritsa 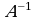 yagona bo‘ladi. Haqiqatan, agar biz
yagona bo‘ladi. Haqiqatan, agar biz  matritsaga teskari boshqa bir
matritsaga teskari boshqa bir 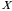 matritsa mavjud desak, ya’ni 1)
matritsa mavjud desak, ya’ni 1)  bo‘lsa, u holda bu tenglikni chap tarafdan
bo‘lsa, u holda bu tenglikni chap tarafdan 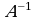 matritsaga ko‘paytirib
matritsaga ko‘paytirib  , 2)
, 2) 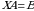 bo‘lsa, u holda bu tenglikni o‘ng tarafdan
bo‘lsa, u holda bu tenglikni o‘ng tarafdan 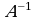 matritsaga ko‘paytirib
matritsaga ko‘paytirib  ga ega bo‘lamiz.
ga ega bo‘lamiz.
2-tеорема. Xos matritsaga teskari matrirsa mavjud emas.
2-misol. Berilgan matritsa:
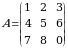
ga teskari matritsani toping:
Yechish. 1)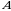 matritsaning determinantini topamiz:
matritsaning determinantini topamiz:

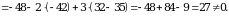
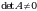 demak,
demak,  mavjud.
mavjud.
2) 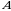 matritsa barcha elementlarining algebraik to‘ldiruvchilarini topamiz:
matritsa barcha elementlarining algebraik to‘ldiruvchilarini topamiz:

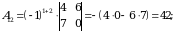
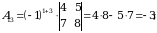
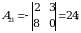
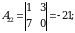
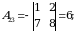

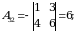
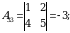
3) 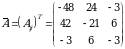 matritsani yozamiz.
matritsani yozamiz.
4)  matritsani topamiz:
matritsani topamiz:

Tekshiramiz:

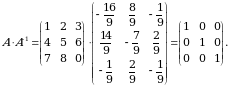
3-misol. Uchburchakli matritsa

uchun teskari matritsani toping.
Yechish. Determinantni hisoblaymiz:
 .
.
Qo‘shma matritsani tuzamiz:

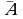 matritsani
matritsani  ga bo‘lib,
ga bo‘lib,
 .
.
Teskari matritsaga ega bo‘lamiz.
Izoh: Uchburchakli matritsaning teskari matritsasining tartibi berilgan matritsaning tartibi bilan bir xil bo‘ladi:
Izoh:Biz yuqorida keltirib chiqargan (***) formula bilan teskari matritsani topish, juda ko‘p hisoblashlarni talab qiladi, shu sababli teskari matritsani topishning bu usuli nazariy jihatdan qulay. Biz quyida amaliyot uchun qulay bo‘lgan usullardan birini koramiz.
Teskari matritsaning asosiy xossalari.
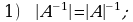
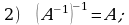
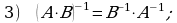
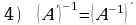 .
.
3 –xossaning isbotini ko‘ramiz:
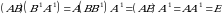 ,
,

bundan
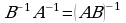 .
.
4 –xossaning isbotini ko‘ramiz:
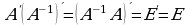 ,
,
bundan
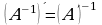 .
.
5-ta’rif. Agar  kvadrat matritsa uchun
kvadrat matritsa uchun 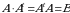 ( ya’ni
( ya’ni 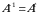 ) bo‘lsa, u holda
) bo‘lsa, u holda  matritsa orthogonal matritsa deyiladi.
matritsa orthogonal matritsa deyiladi.
3-tеорема. Har qanday orthogonal matritsa uchun teskari matritsa mavjud va u ham orthogonal matritsa bo‘ladi.
Bu teorema  bolganidan ,
bolganidan ,  kelib chiqadi.
kelib chiqadi.
4-tеорема. Orthogonal matritsalarning ko‘paytmasi ham orthogonal matritsa bo‘ladi.
3.Ekvivalent almashtirishlar yordamida teskari matritsani hisoblash.
Teskari matritsani topishning Gauss-Jordan usulida maxsusmas matritsani shu tartibdagi birlik matritsa bilan kengaytiriladi, kengaytirilgan matritsa satrlari ustida elementar almashtirish to kengaytirilgan matritsa birinchi qismida birlik matritsa hosil boʻlguncha olib boriladi, natijada kengaytirilgan matritsaning ikkinchi qismida berilgan matritsaga teskari boʻlgan matritsa hosil boʻladi. Bu jarayonni Gauss-Jordan modifikatsiyasi (yoki formulasi) koʻrinishida yozishimiz mumkin: 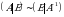
4-misol. Gauss-Jordan usulida berilgan matritsaga teskari matritsani toping.

Yechish. 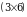 o‘lchamli
o‘lchamli  kengaytirilgan matritsani yozamiz. Avval matritsaning satrlari ustida elementar almashtirishlar bajarib uni pog‘onasimon ko‘rinishga keltiramiz
kengaytirilgan matritsani yozamiz. Avval matritsaning satrlari ustida elementar almashtirishlar bajarib uni pog‘onasimon ko‘rinishga keltiramiz 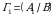 , keyin
, keyin  ko‘rinishga keltiramiz.
ko‘rinishga keltiramiz.
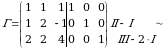
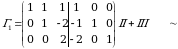
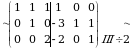


Demak, 
Tekshiramiz:


Endi teskari matritsani Excelda qurish bilan tanishib chiqamiz.
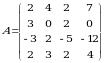
matritsaning teskarisini topamiz. Birinchi navbatda matritsaning determinantini hisoblaymiz.  . Demak, teskari matritsa mavjud.
. Demak, teskari matritsa mavjud.
I. Boʻsh katakni belgilaymiz. Matematik funksiyalardan 'МОБР' funksiyasini tanlaymiz.
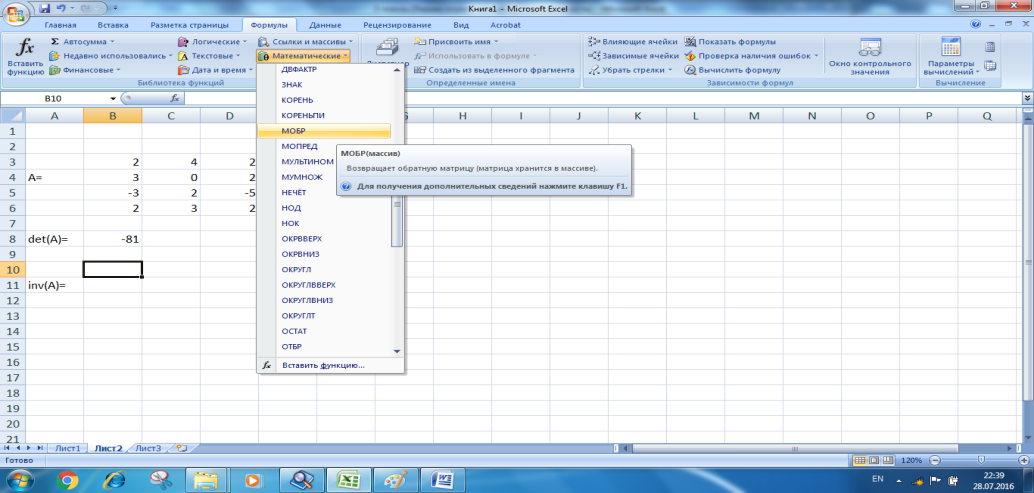
II. Dialog oynasida  matritsa joylashgan oʻrni koordinatalarini kiritamiz.
matritsa joylashgan oʻrni koordinatalarini kiritamiz.
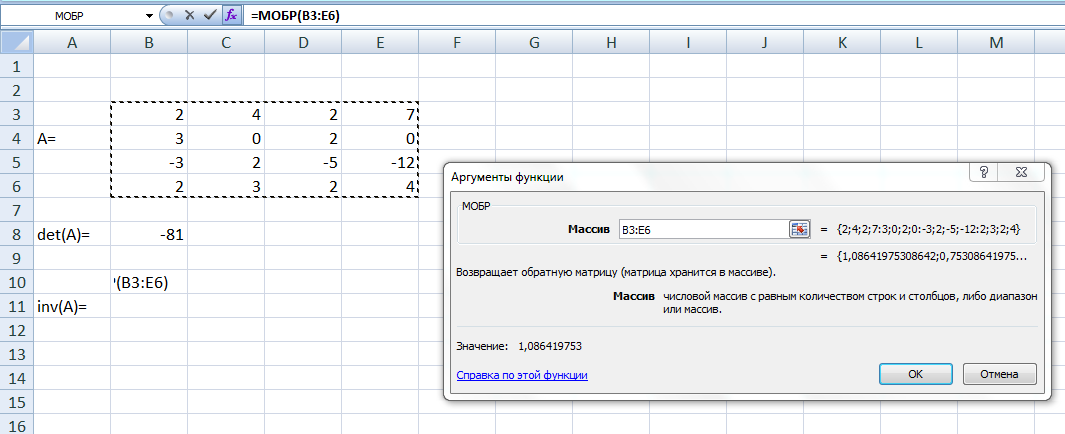
III. Enter tugmasini bosamiz. Belgilangan katakda teskari matritsaning birinchi elementi paydo boʻladi. Boshqa elementlarni hosil qilish uchun shu katakdan boshlab 4 ga 4 jadvalni belgilaymiz va  tugmasini bosamiz. Keyin Ctrl+Shift+Enter tugmalari birgalikda bosiladi. Shu bilan teskari matritsani hosil qilamiz.
tugmasini bosamiz. Keyin Ctrl+Shift+Enter tugmalari birgalikda bosiladi. Shu bilan teskari matritsani hosil qilamiz.
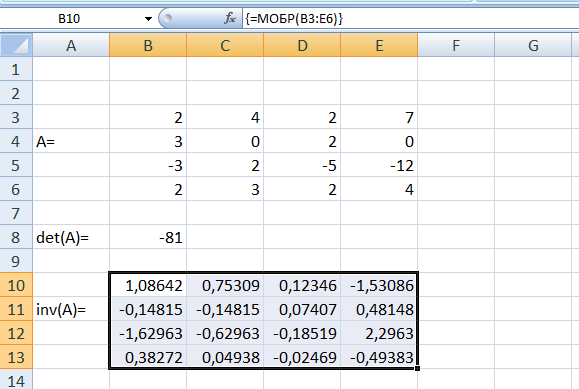
Matritsalarni koʻpaytirish usuli bilan tekshirib, natija toʻg’riligiga ishonch hosil qilishimiz mumkin.

O‘z-o‘zini tekshirish uchun savollar
Xosmas matritsa deb qanday kvadratik matritsaga aytiladi?
Xos matritsa deb qanday kvadratik matritsaga aytiladi?
Teng tartibli qanday kvadratik matritsalarni ko’paytirganda ko’paytma xosmas matritsadan iborat bo’ladi?
Xosmas matritsaning teskari matritsasi deb qanday matritsaga aytiladi?
Nima uchun xos matritsaning teskarisi mavjud emas?
Kvadratik matritsaning teskari matritsasini qurishning qanday usullarini bilasiz?
Teskari matritsaning qanday xossalarini bilasiz?
Asosiy adabiyotlar:
Gilbert Strang “Introduction to Linear Algebra”, USA, Cambridge press,  Edition, 2016.
Edition, 2016.
Grewal B.S. “Higher Engineering Mathematics”, Delhi, Khanna publishers,  Edition, 2012.
Edition, 2012.
Raxmatov R.R., Adizov A.A., Tadjibayeva Sh.E., Shoimardonov S.K. Chiziqli algebra va analitik geometriya. O‘quv qollanma. Toshkent 2020.
Rаxмаtоv R.R., Adizov A.A. “Chiziqli fazo va chiziqli operatorlar” O‘quv uslubiy qollanma. TATU, Toshkent 2019.
Соатов Ё.У. “Олий математика”, Т., Ўқитувчи нашриёти, 1- 5 қисмлар, 1995.
Рябушко А.П. и др. “Сборник индивидуальных заданий по высшей математике”, Минск, Высшая школа, 1-3 частях, 1991.
Asosiy adabiyotlar:
Мирзиёев Ш. Буюк келажагимизни мард ва олижаноб халқимиз билан бирга қурамиз. –Т.: Ўзбекистон, 2017. - 488 бет.
Мирзиёев Ш.М. Қонун устуворлиги ва инсон манфаатларини таъминлаш-юрт тараққиёти ва халқ фаровонлигининг гарови. –Т.: Ўзбекистон, 2017.
Мирзиёев Ш.М. Эркин ва фаровон, демократик Ўзбекистон давлатини биргаликда барпо этамиз. Т.: Ўзбекистон, 2017.
Adizov A.A., Xudoyberganov M.O‘. Amaliy matematika. O‘quv uslubiy qo‘llanma. Toshkent. 2014.
Шодиев Т.Ш. Аналитик геометрия ва чизиқли алгебра. Тошкент “Ўқитувчи” 1984.
Ильин В. А., Позняк Э. Г. Линейная алгебра. — 6-е изд., стер. — М.: ФИЗМАТЛИТ, 2004.
Задорожный В. Н. и др. Высшая математика для технических
университетов. Часть I. Линейная алгебра. - Томск: Изд-во ТПУ, 2009.
Данко П.С., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Седьмое издание. -М.: Высшая; школа, 2015.
Семёнова Т.В. Высшая математика: учебное пособие для студентов технических вузов. Часть 1. - Пенза: Пензенский гос. ун-т, 2008.
Макаров Е. В., Лунгу К. Н. Высшая математика: руководство к решению задач: учебное пособие, Часть 1, Физматлит. 2013.
Минорский В.И. Сборник задач по высшей математике. М: Наука, 1987.
Беклемешев Д.В., Петрович А.Ю., Чуберов И.А. Сборник задач по аналитической геометрии и линейной алгебре. -М.: Наука, 1987.
Бугров Я.С., Николский С.М. Сборник задач по высшей математике, - М.: Наука. 1997.







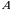 kvadrat matritsaning har bir
kvadrat matritsaning har bir  elementini unga mos algebraik toʻldiruvchisi bilan almashtirish natijasida hosil qilingan matritsa ustida transponirlash amalini bajarishdan hosil boʻlgan
elementini unga mos algebraik toʻldiruvchisi bilan almashtirish natijasida hosil qilingan matritsa ustida transponirlash amalini bajarishdan hosil boʻlgan  matritsa berilgan matritsaga qoʻshma matritsa deyiladi.
matritsa berilgan matritsaga qoʻshma matritsa deyiladi.

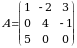 matritsa uchun qoʻshma matritsa topilsin.
matritsa uchun qoʻshma matritsa topilsin.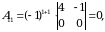

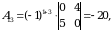
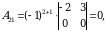

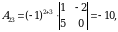
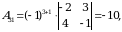
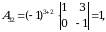
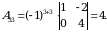
 matritsa
matritsa
 kvadrat matritsaning determinanti noldan farqli bo‘lsa, ya’ni
kvadrat matritsaning determinanti noldan farqli bo‘lsa, ya’ni  bo‘lsa,
bo‘lsa,  bo‘lsa,
bo‘lsa,  kvadrat matritsa uchun
kvadrat matritsa uchun 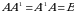 tenglik bajarilsa, u holda
tenglik bajarilsa, u holda 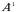 matritsa
matritsa 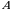 matritsaga teskari matritsa deyiladi.
matritsaga teskari matritsa deyiladi.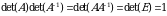 boʻladi. Bundan, agar teskari matritsa mavjud boʻlsa
boʻladi. Bundan, agar teskari matritsa mavjud boʻlsa 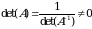 ekanligini kelib chiqadi.
ekanligini kelib chiqadi. bo‘lsin..
bo‘lsin..  matritsani quramiz
matritsani quramiz
 va
va 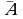 matritsalar ko‘paytmasini qaraymiz:
matritsalar ko‘paytmasini qaraymiz: .
.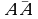 ko‘paytmaning har bir elementi
ko‘paytmaning har bir elementi 
 ,
,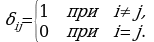
 .
.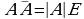 . (*)
. (*)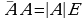 (**)
(**) ,
, (***)
(***)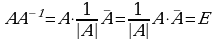 ,
,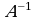 matritsa
matritsa 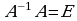 .
.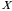 matritsa mavjud desak, ya’ni 1)
matritsa mavjud desak, ya’ni 1)  bo‘lsa, u holda bu tenglikni chap tarafdan
bo‘lsa, u holda bu tenglikni chap tarafdan  , 2)
, 2) 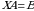 bo‘lsa, u holda bu tenglikni o‘ng tarafdan
bo‘lsa, u holda bu tenglikni o‘ng tarafdan 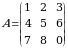
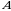 matritsaning determinantini topamiz:
matritsaning determinantini topamiz:
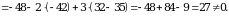
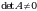 demak,
demak,  mavjud.
mavjud.
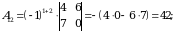
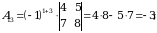
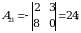
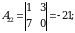
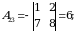

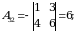
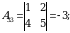
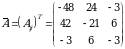 matritsani yozamiz.
matritsani yozamiz.

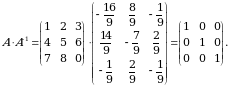

 .
.
 ga bo‘lib,
ga bo‘lib,  .
.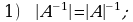
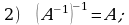
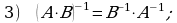
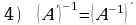 .
.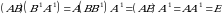 ,
,
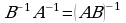 .
.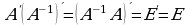 ,
,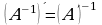 .
.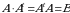 ( ya’ni
( ya’ni 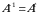 ) bo‘lsa, u holda
) bo‘lsa, u holda  bolganidan ,
bolganidan ,  kelib chiqadi.
kelib chiqadi.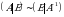

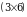 o‘lchamli
o‘lchamli  kengaytirilgan matritsani yozamiz. Avval matritsaning satrlari ustida elementar almashtirishlar bajarib uni pog‘onasimon ko‘rinishga keltiramiz
kengaytirilgan matritsani yozamiz. Avval matritsaning satrlari ustida elementar almashtirishlar bajarib uni pog‘onasimon ko‘rinishga keltiramiz 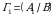 , keyin
, keyin  ko‘rinishga keltiramiz.
ko‘rinishga keltiramiz. 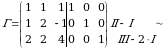
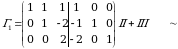
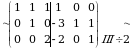





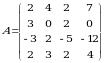
 . Demak, teskari matritsa mavjud.
. Demak, teskari matritsa mavjud.

 tugmasini bosamiz. Keyin Ctrl+Shift+Enter tugmalari birgalikda bosiladi. Shu bilan teskari matritsani hosil qilamiz.
tugmasini bosamiz. Keyin Ctrl+Shift+Enter tugmalari birgalikda bosiladi. Shu bilan teskari matritsani hosil qilamiz.

 Edition, 2016.
Edition, 2016.  Edition, 2012.
Edition, 2012. 
















