

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Тема 7. Многогранники
Категория:
Математика
30.03.2021 16:42
Просмотр содержимого документа
«46. понятие многогранника»
Просмотр содержимого документа
«47. призма»
Просмотр содержимого документа
«48. пирамида»
Просмотр содержимого документа
«49. Площади многог»
Просмотр содержимого документа
«50. Правильные многогранники»
Просмотр содержимого документа
«51. Понятие объема»
Просмотр содержимого документа
«52. Объем призмы»
Просмотр содержимого документа
«53. Объем пирамиды»
Просмотр содержимого документа
«54. обобщение»
Просмотр содержимого документа
«Меры объема»
© 2021, Графова Татьяна Владимировна 1184 2




 дной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора. Отличительным знаком пифагорейцев была пентаграмма, на языке математики- это правильный невыпуклый или звездчатый пятиугольник. Пентаграмме присваивалось способность защищать человека от злых духов.
дной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора. Отличительным знаком пифагорейцев была пентаграмма, на языке математики- это правильный невыпуклый или звездчатый пятиугольник. Пентаграмме присваивалось способность защищать человека от злых духов.



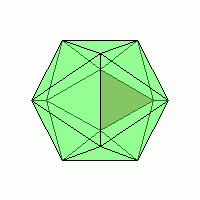
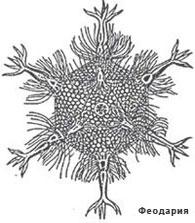 равильные многогранники встречаются так же и в живой природе. Например, скелет одноклеточного организма феодарии (Circjgjnia icosahtdra) по форме напоминает икосаэдр.
равильные многогранники встречаются так же и в живой природе. Например, скелет одноклеточного организма феодарии (Circjgjnia icosahtdra) по форме напоминает икосаэдр.
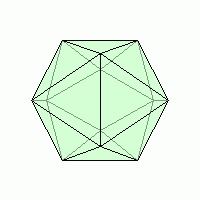
 Ребро многогранника
Ребро многогранника 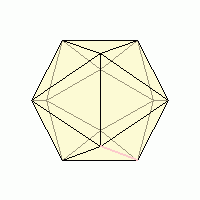



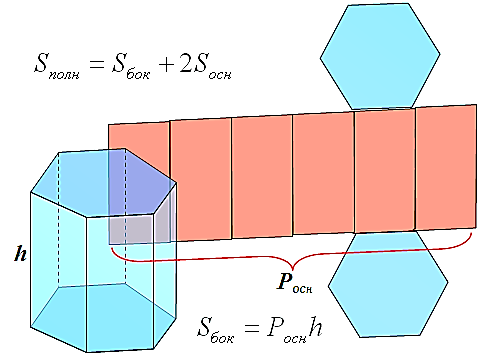
 ЕОРЕМА
ЕОРЕМА
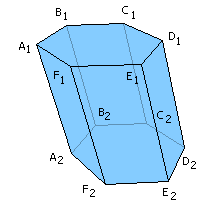
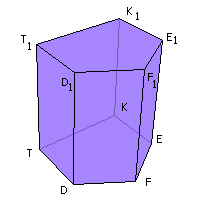 усть для определённости дана прямая пятиугольная призма TKEFDT
усть для определённости дана прямая пятиугольная призма TKEFDT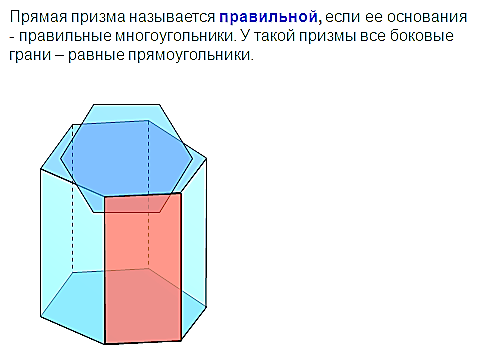
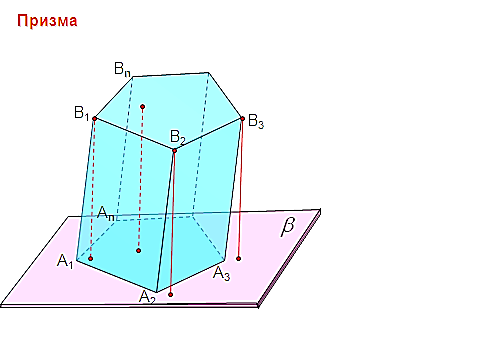
 араллелепипед
араллелепипед адача №1
адача №1
 адача №3
адача №3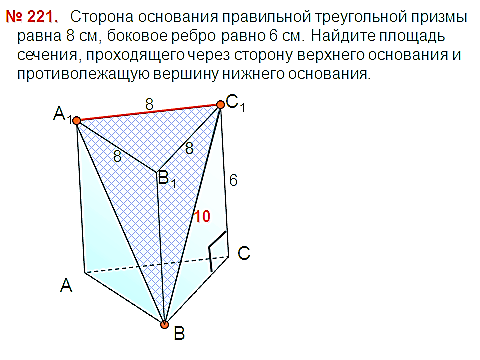 адача №7
адача №7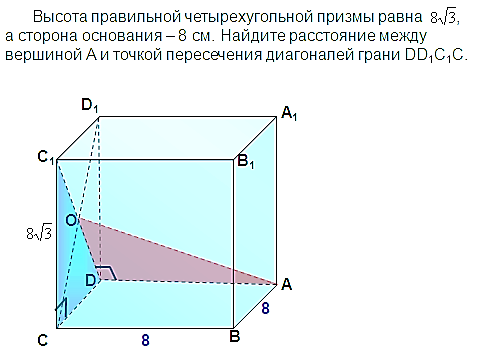
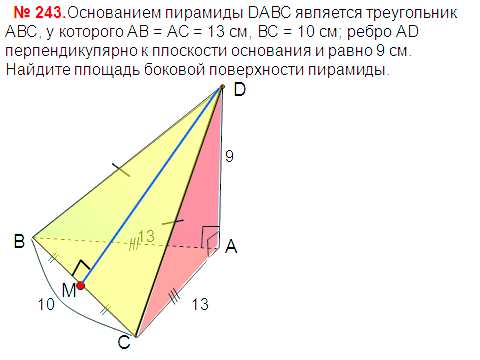
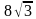 см, а сторона основания – 8 см. Найдите расстояние между вершиной А и точкой пересечения диагоналей грани
см, а сторона основания – 8 см. Найдите расстояние между вершиной А и точкой пересечения диагоналей грани 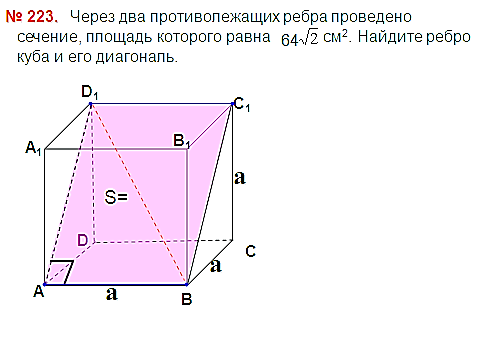 адача №9
адача №9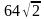 см2. Найдите ребро куба и его диагональ.
см2. Найдите ребро куба и его диагональ.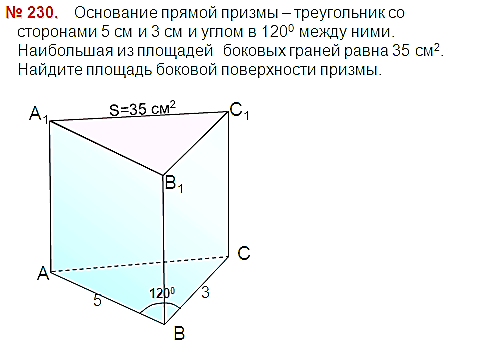
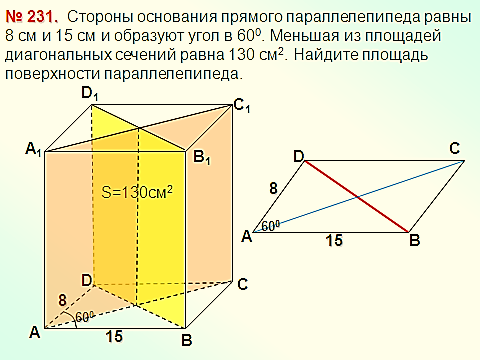 тороны основания прямого параллелепипеда равны 8 см и 15 см и образуют угол в 600. Меньшая из площадей диагональных сечений равна 130 см2. Найдите площадь поверхности параллелепипеда.
тороны основания прямого параллелепипеда равны 8 см и 15 см и образуют угол в 600. Меньшая из площадей диагональных сечений равна 130 см2. Найдите площадь поверхности параллелепипеда.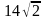
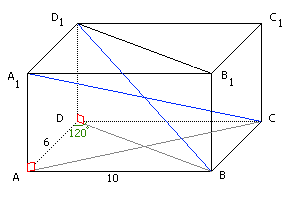
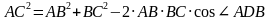 ,
, 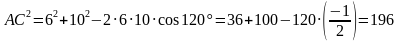 ;
; .
.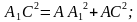
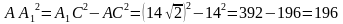

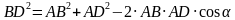 ,
,  ;
; .
.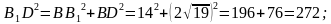
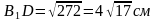

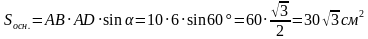 ,
,
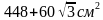
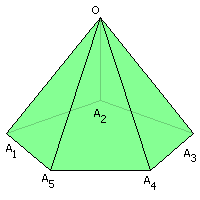


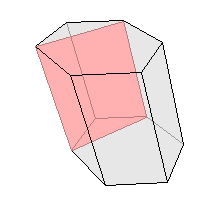
 иагональным сечением пирамиды
иагональным сечением пирамиды
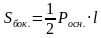
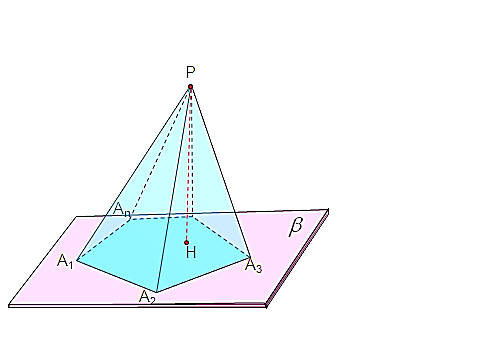
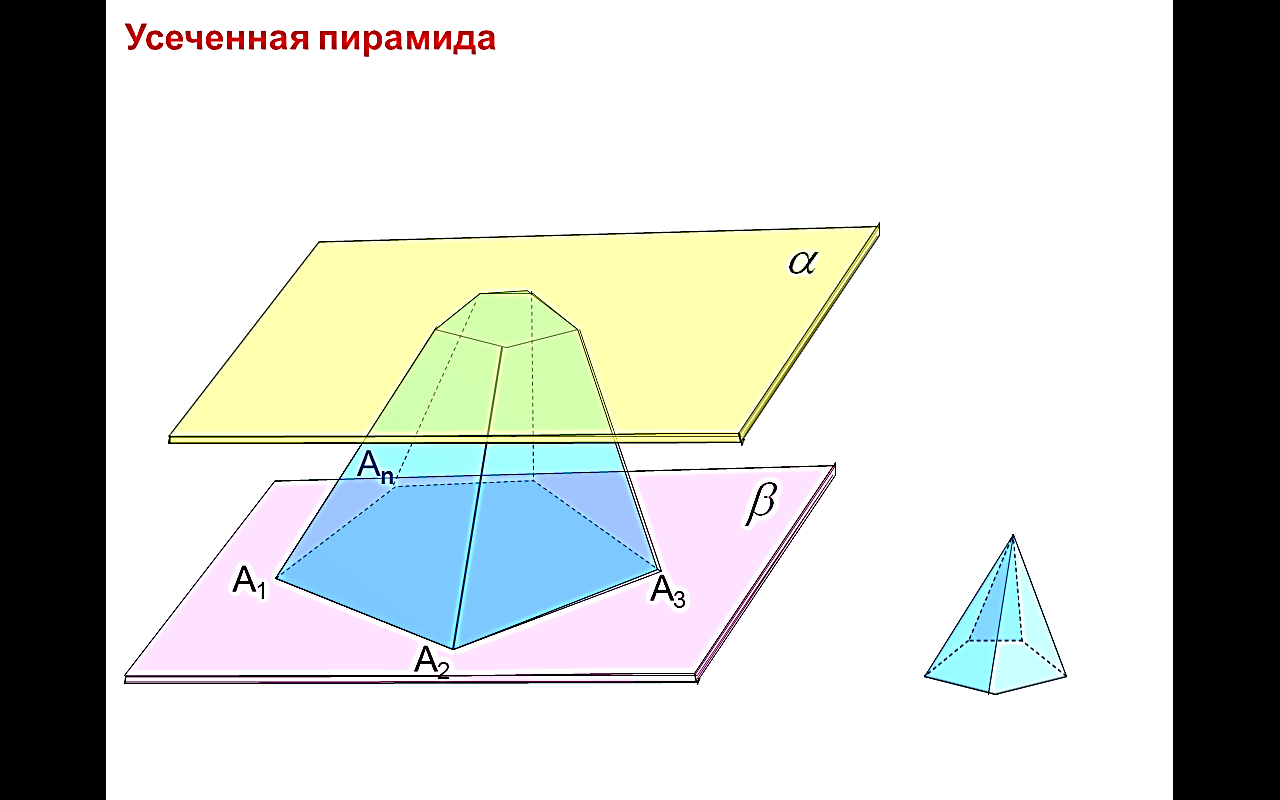
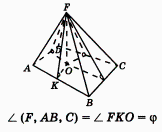
 оказательство проведём для правильной шестиугольной пирамиды TABCDEF:
оказательство проведём для правильной шестиугольной пирамиды TABCDEF:
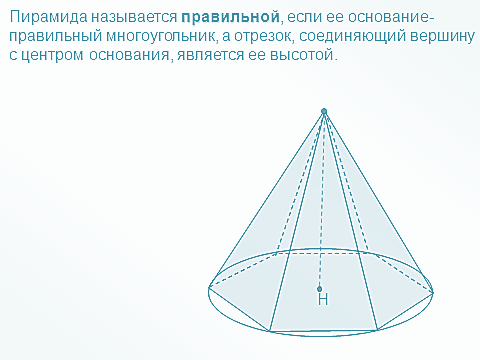
 ентром правильного многоугольника называется центр вписанной (или описанной около него окружности).
ентром правильного многоугольника называется центр вписанной (или описанной около него окружности).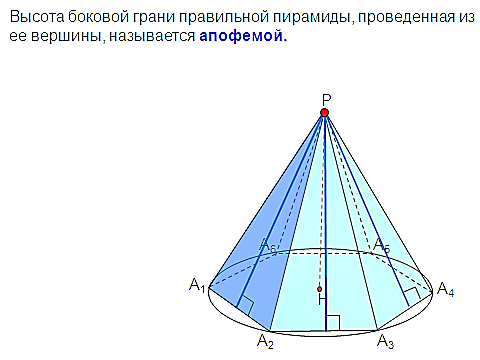 се боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.
се боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.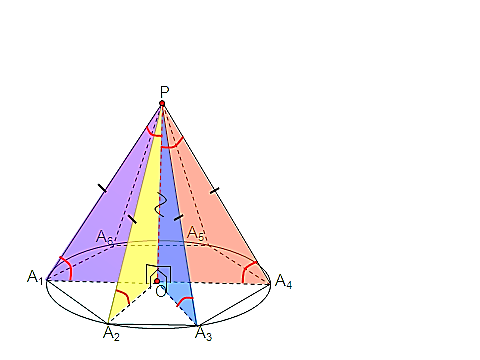 сли боковые ребра равны
сли боковые ребра равны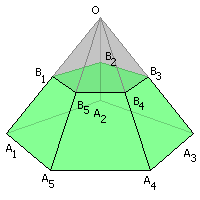
 адача №1
адача №1 адача №2
адача №2
 адача №4
адача №4 адача №5
адача №5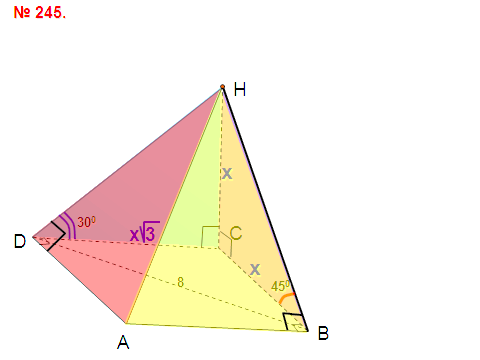
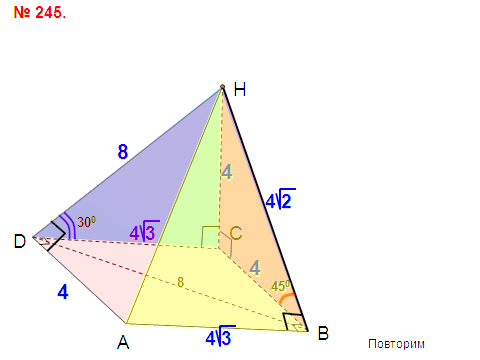 снованием пирамиды является прямоугольник, диагональ которого равна 8 см. Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы в 300 и 450. Найдите
снованием пирамиды является прямоугольник, диагональ которого равна 8 см. Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы в 300 и 450. Найдите 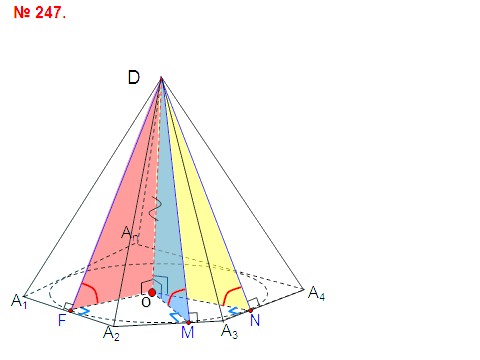 вугранные углы при основании пирамиды равны. Докажите, что: а) высота пирамиды проходит через центр окружности, вписанной в основание; б) высоты всех боковых граней, проведенные из вершины пирамиды, равны; в) площадь боковой поверхности пирамиды равна половине произведения периметра основания на высоту боковой грани, проведенную из вершины.
вугранные углы при основании пирамиды равны. Докажите, что: а) высота пирамиды проходит через центр окружности, вписанной в основание; б) высоты всех боковых граней, проведенные из вершины пирамиды, равны; в) площадь боковой поверхности пирамиды равна половине произведения периметра основания на высоту боковой грани, проведенную из вершины. 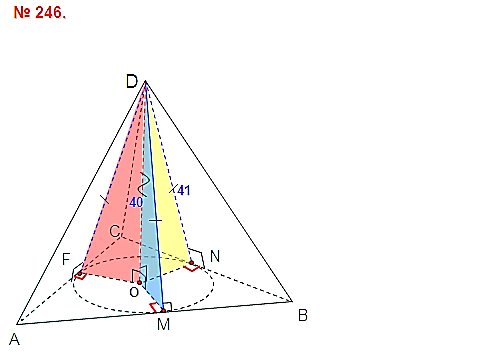 адача №8
адача №8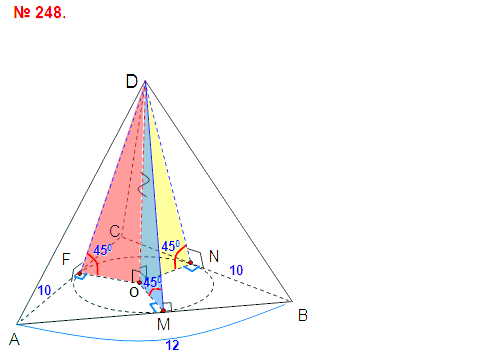 адача №9
адача №9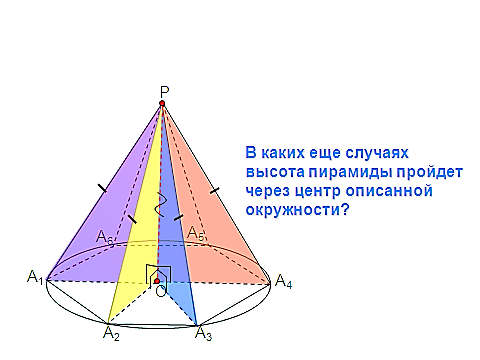 пирамиде все боковые ребра равны между собой. Докажите, что: а) высота пирамиды проходит через центр окружности, описанной около основания; б) все боковые ребра составляют равные углы с плоскостью основания.
пирамиде все боковые ребра равны между собой. Докажите, что: а) высота пирамиды проходит через центр окружности, описанной около основания; б) все боковые ребра составляют равные углы с плоскостью основания.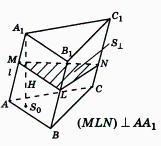
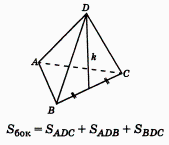
 адача №1
адача №1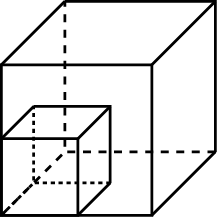 адача №2
адача №2 адача №3
адача №3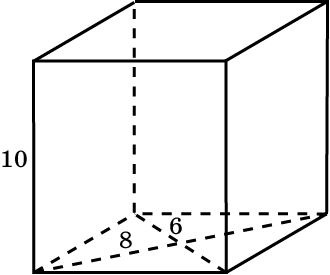
 адача №6
адача №6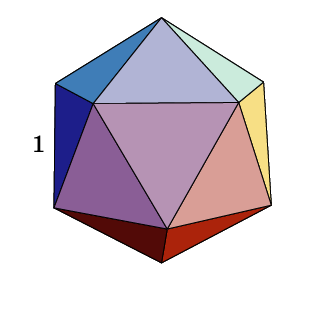 адача №7
адача №7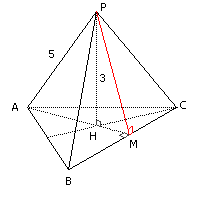
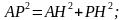

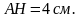

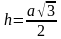
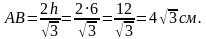

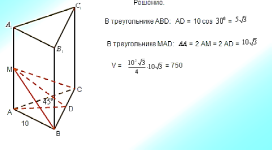
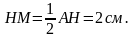 По теореме Пифагора имеем:
По теореме Пифагора имеем: 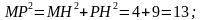
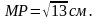
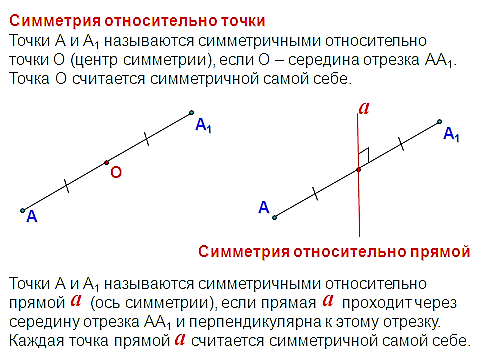
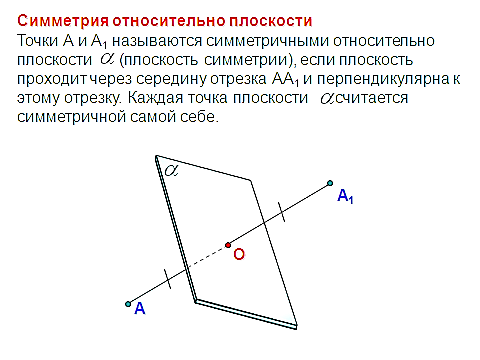
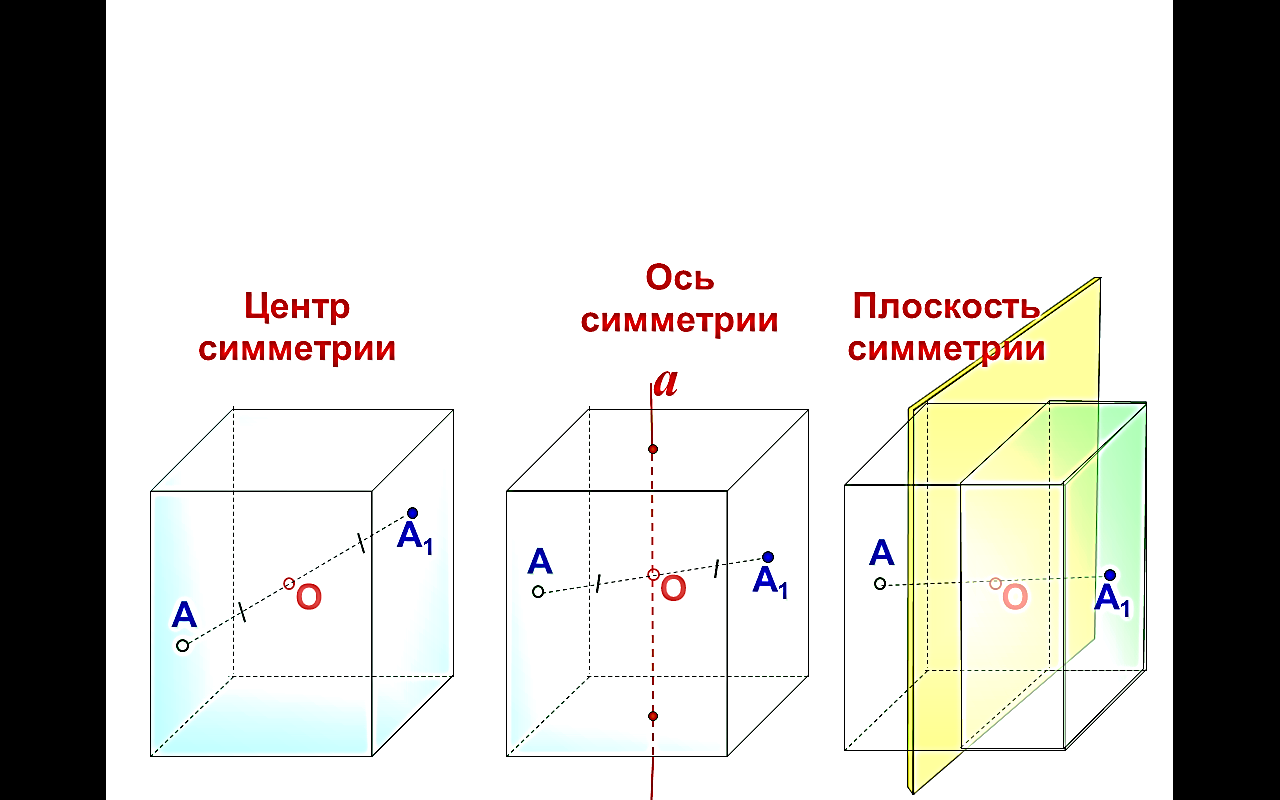

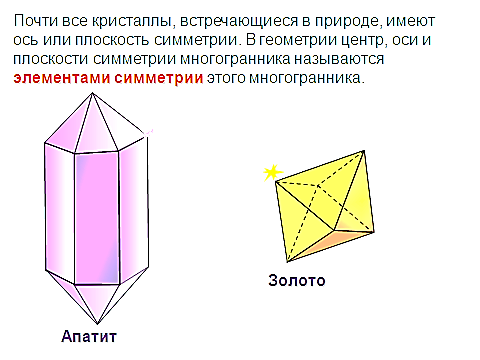
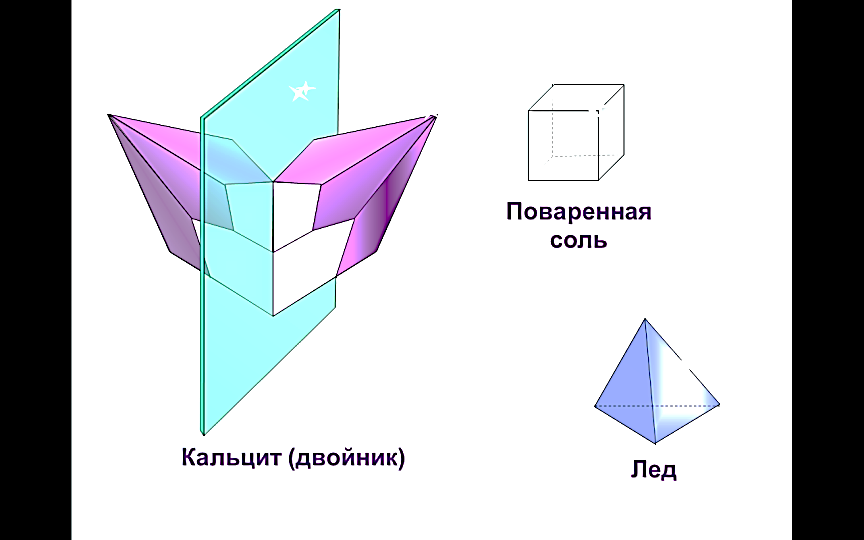
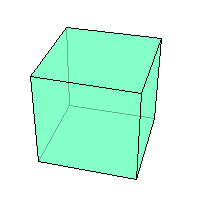
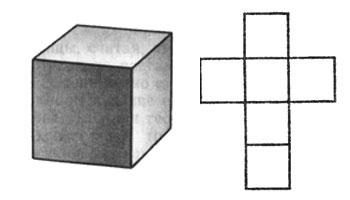 редставляет собой квадрат. Частный случай параллелепипеда и призмы.
редставляет собой квадрат. Частный случай параллелепипеда и призмы.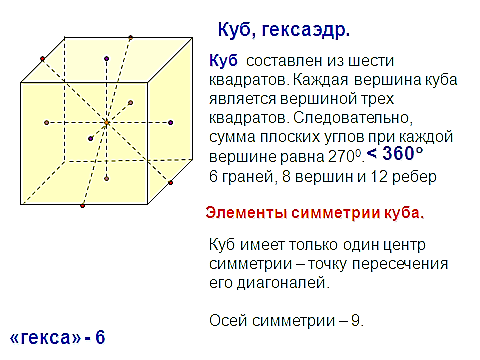
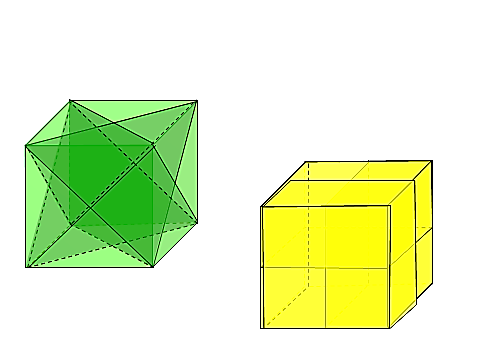
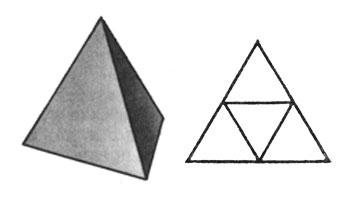
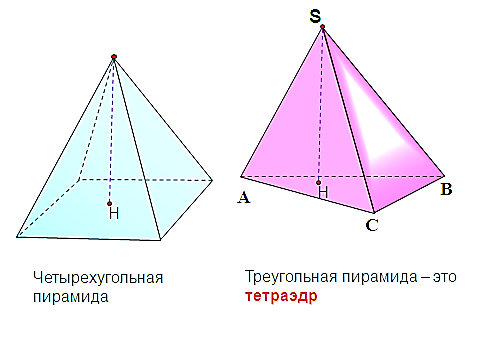
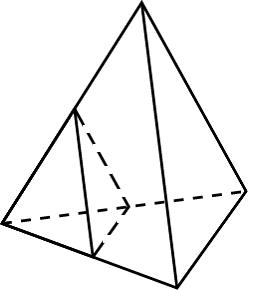
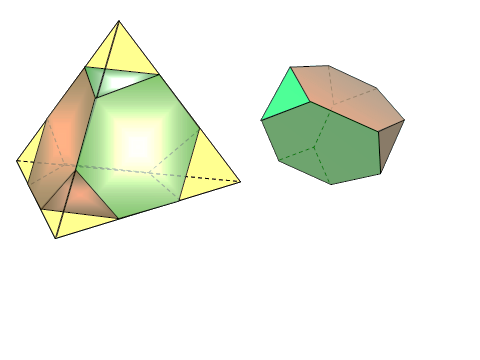
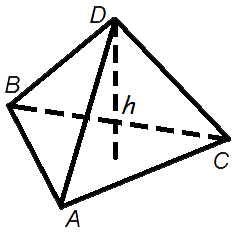
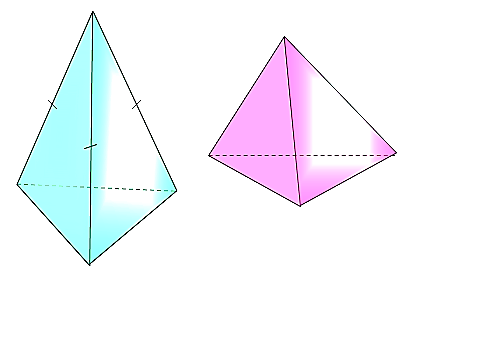 етраэдр (четырёхгранник) — многогранник с четырьмя треугольными гранями, в каждой из вершин которого сходятся по 3 грани. У тетраэдра 4 грани, 4 вершины и 6 рёбер. Параллельные плоскости, проходящие через пары скрещивающихся рёбер тетраэдра, определяют описанный около тетраэдра параллелепипед. Отрезок, соединяющий вершину тетраэдра с точкой пересечения медиан противоположной грани, называется его медианой, опущенной из данной вершины. Отрезок, соединяющий середины скрещивающихся рёбер тетраэдра, называется его бимедианой, соединяющей данные рёбра. Отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани, называется его высотой, опущенной из данной вершины.
етраэдр (четырёхгранник) — многогранник с четырьмя треугольными гранями, в каждой из вершин которого сходятся по 3 грани. У тетраэдра 4 грани, 4 вершины и 6 рёбер. Параллельные плоскости, проходящие через пары скрещивающихся рёбер тетраэдра, определяют описанный около тетраэдра параллелепипед. Отрезок, соединяющий вершину тетраэдра с точкой пересечения медиан противоположной грани, называется его медианой, опущенной из данной вершины. Отрезок, соединяющий середины скрещивающихся рёбер тетраэдра, называется его бимедианой, соединяющей данные рёбра. Отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани, называется его высотой, опущенной из данной вершины.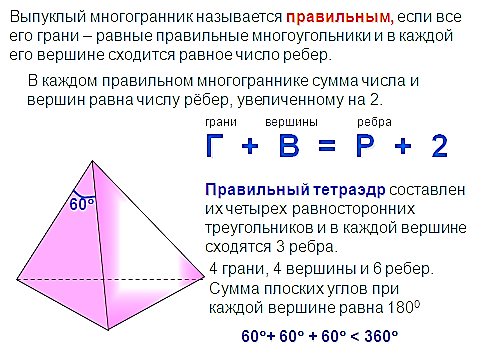 оставлен их четырех равносторонних треугольников;
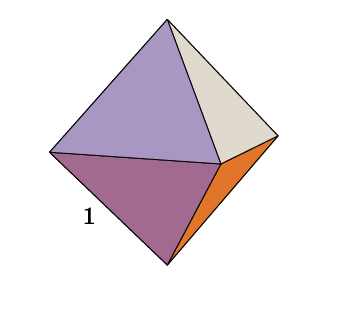
оставлен их четырех равносторонних треугольников;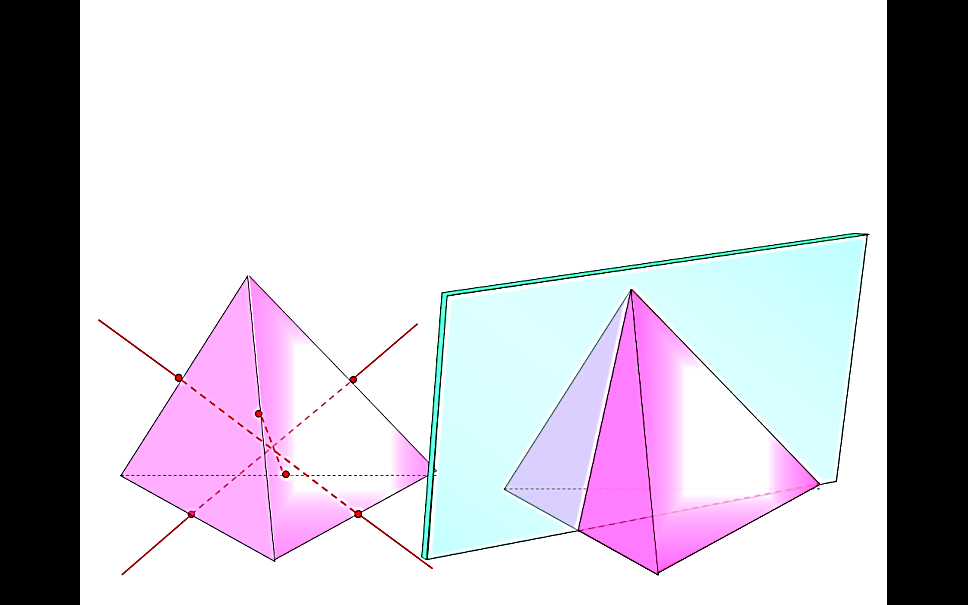 лоскостей симметрии – 6.
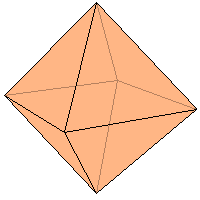
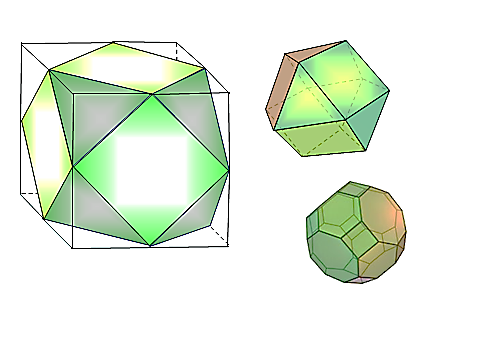
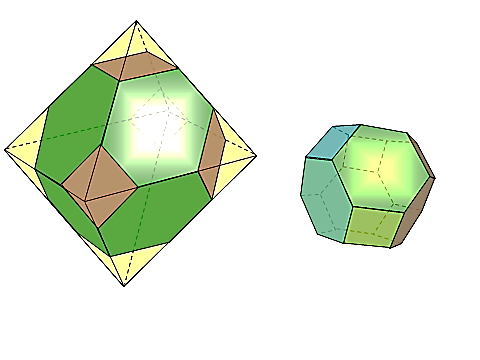
лоскостей симметрии – 6.  ильных многогранников, так называемых, Платоновых тел. Октаэдр имеет 8 треугольных граней, 12 рёбер, 6 вершин, в каждой его вершине сходятся 4 ребра.
ильных многогранников, так называемых, Платоновых тел. Октаэдр имеет 8 треугольных граней, 12 рёбер, 6 вершин, в каждой его вершине сходятся 4 ребра.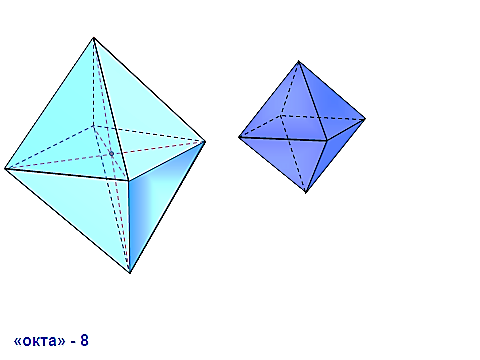
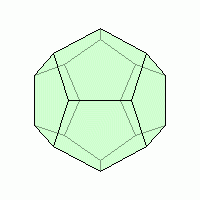
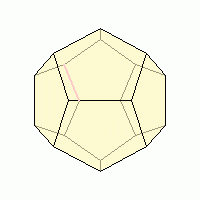
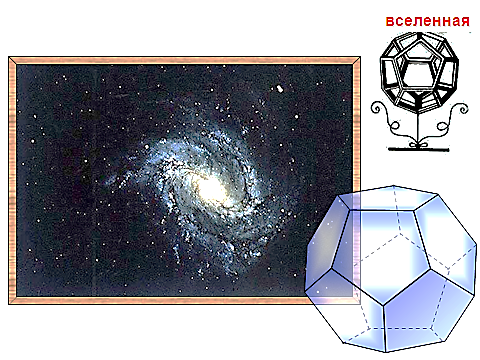
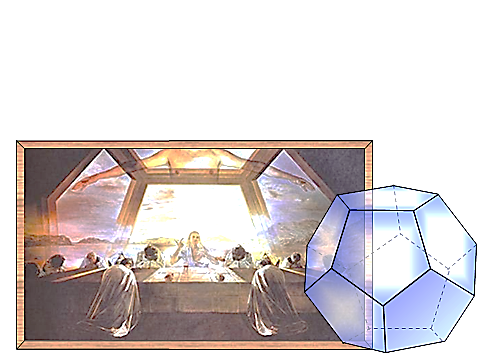
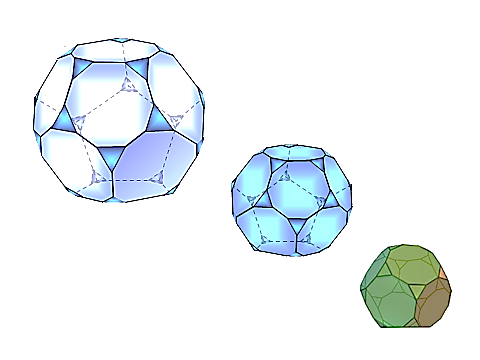
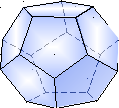 Додекаэдр, двенадцатигранник — правильный многог
Додекаэдр, двенадцатигранник — правильный многог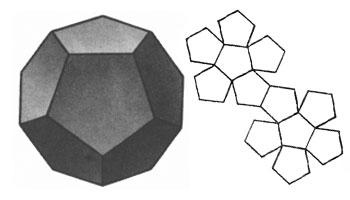 ранник, составленный из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Таким образом, додекаэдр имеет 12 граней (пятиугольных), 30 рёбер и 20 вершин (в каждой сходятся 3 ребра. Сумма плоских углов при каждой из 20 вершин равна 324°.
ранник, составленный из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Таким образом, додекаэдр имеет 12 граней (пятиугольных), 30 рёбер и 20 вершин (в каждой сходятся 3 ребра. Сумма плоских углов при каждой из 20 вершин равна 324°. Первым свойства правильных многогранников описал древнегреческий ученый Платон (428 – 348 г. до н.э.). Именно поэтому правильные многогранники называют также телами Платона.
Первым свойства правильных многогранников описал древнегреческий ученый Платон (428 – 348 г. до н.э.). Именно поэтому правильные многогранники называют также телами Платона.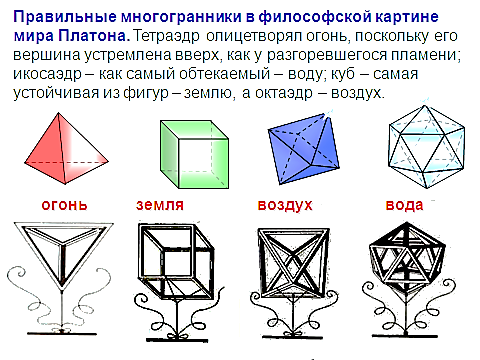











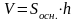

 лощади основания на высоту
лощади основания на высоту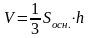

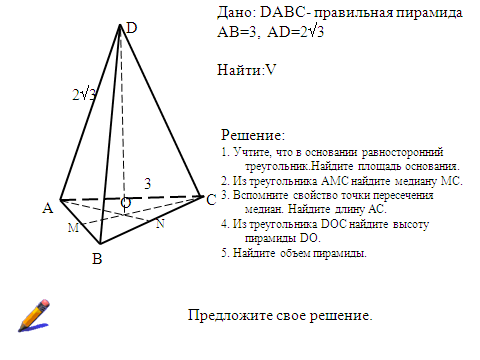
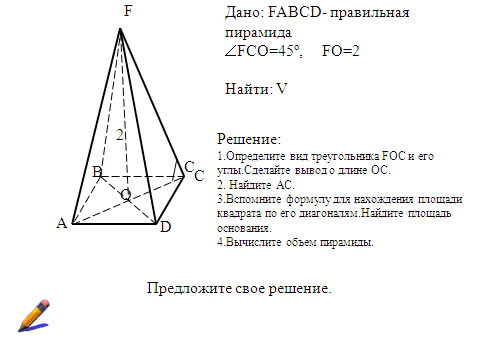
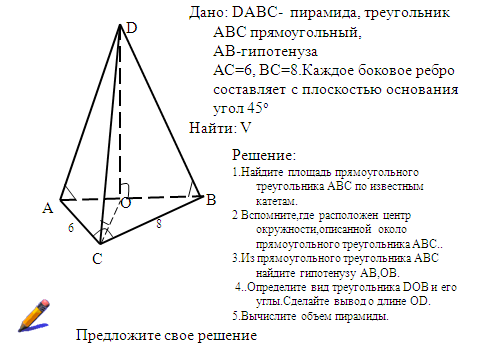

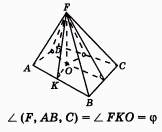
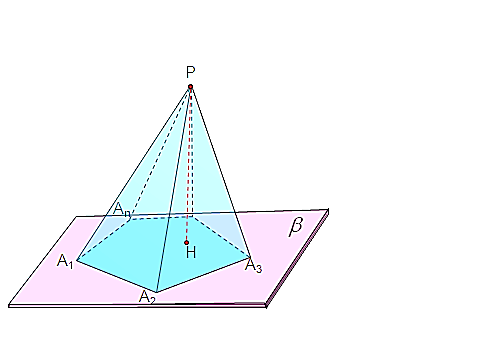 ирамидой
ирамидой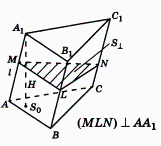
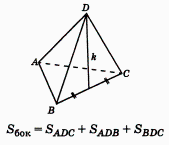
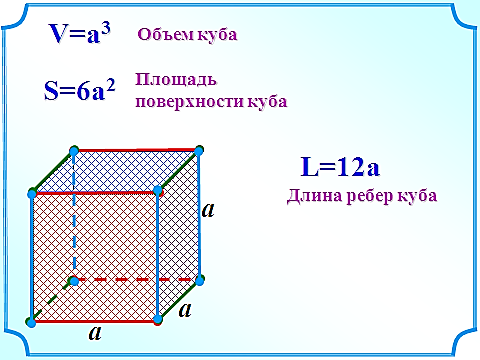
 бъем куба равен кубу длины его грани.
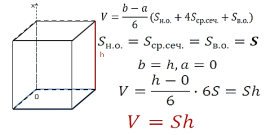
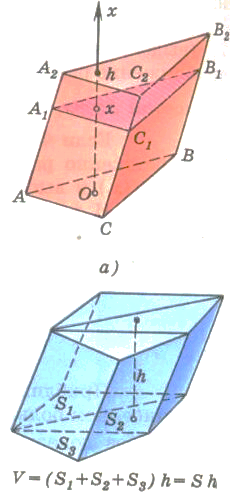
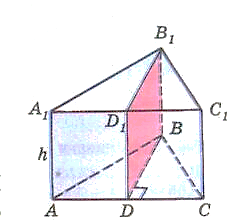
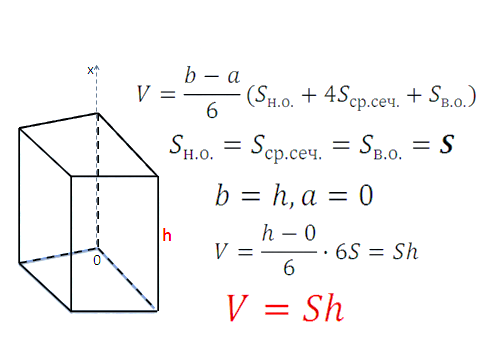
бъем куба равен кубу длины его грани.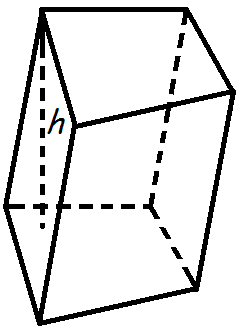 бъем призмы равен произведению площади основания призмы, на высоту.
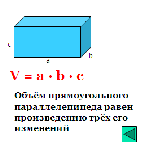
бъем призмы равен произведению площади основания призмы, на высоту.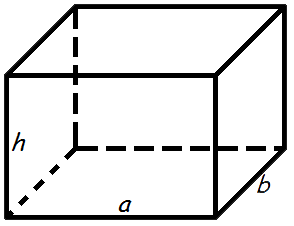 бъем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
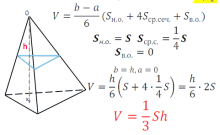
бъем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.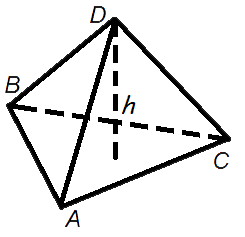 бъем пирамиды равен трети от произведения площади ее основания на высоту.
бъем пирамиды равен трети от произведения площади ее основания на высоту.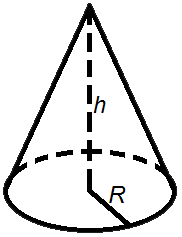 бъем конуса равен трети от произведению площади его основания на высоту.
бъем конуса равен трети от произведению площади его основания на высоту. бъем шара равен четырем третим от его радиуса в кубе помноженого на число пи.
бъем шара равен четырем третим от его радиуса в кубе помноженого на число пи.

















