СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Тема 6. Введение в стереометрию
Категория:
Математика
30.03.2021 16:41
Просмотр содержимого документа
«16. Основные понятие стереометрии»
Просмотр содержимого документа
«17. Призма. Пирамида.»
Просмотр содержимого документа
«18. Взаимное расположение точек»
Просмотр содержимого документа
«19. Взаимное расположение точек»
Просмотр содержимого документа
«20. Построение сечений многогранников»
Просмотр содержимого документа
«21. Построение сечений многогранников»
Просмотр содержимого документа
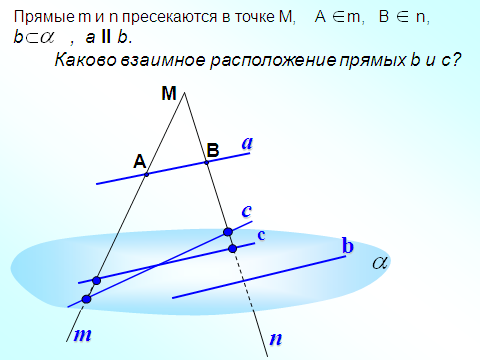
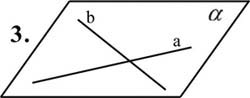
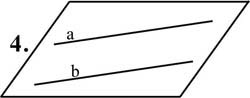
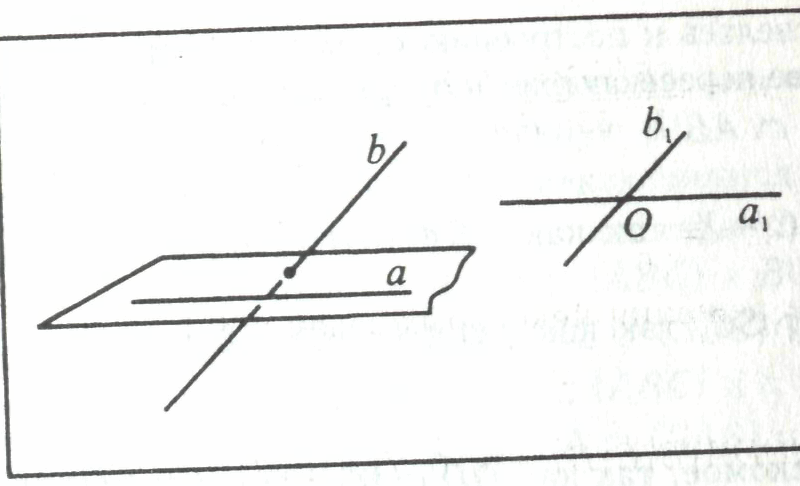
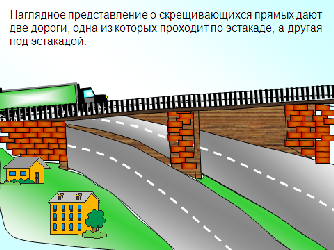
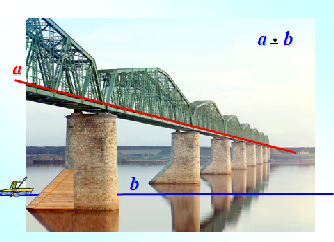
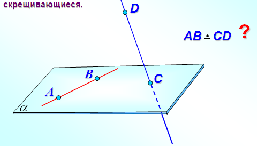
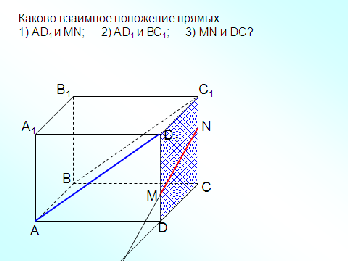
«22. Взаимное расположение двух прямых в пространстве»
Просмотр содержимого документа
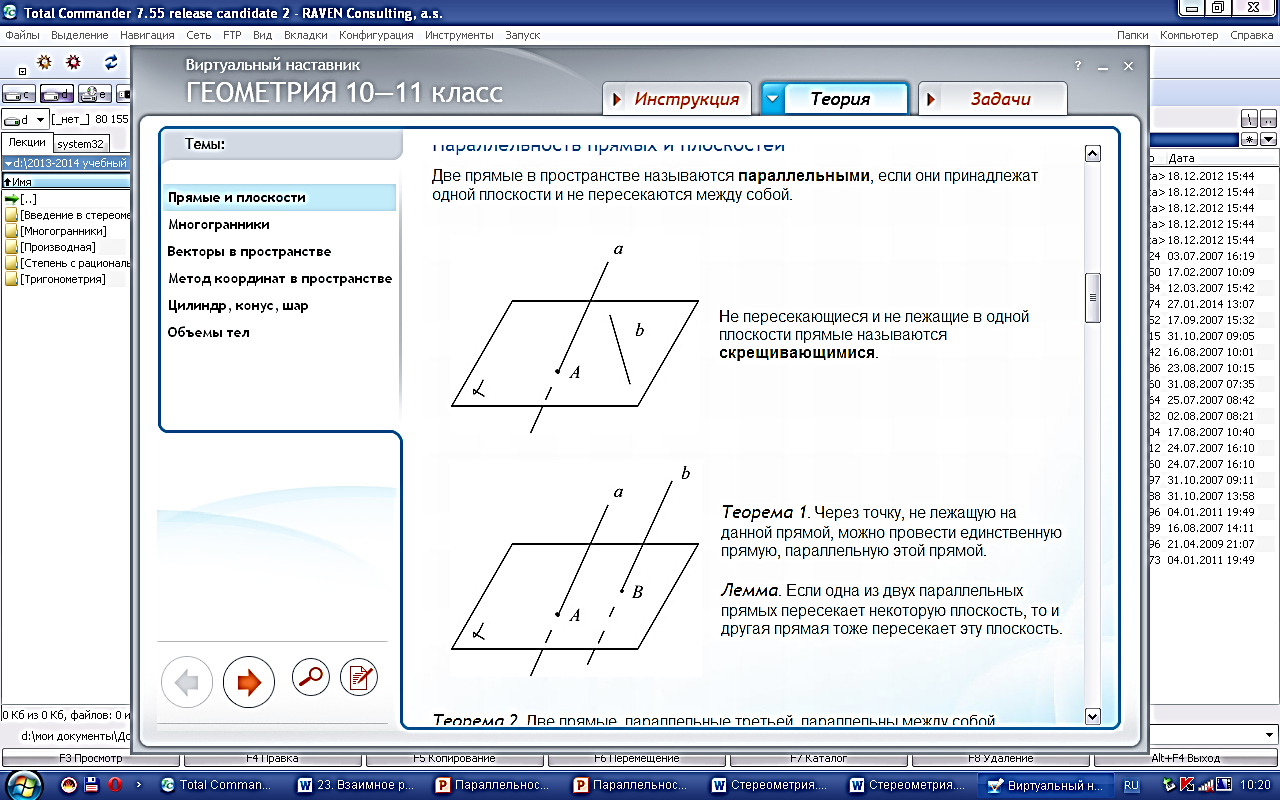
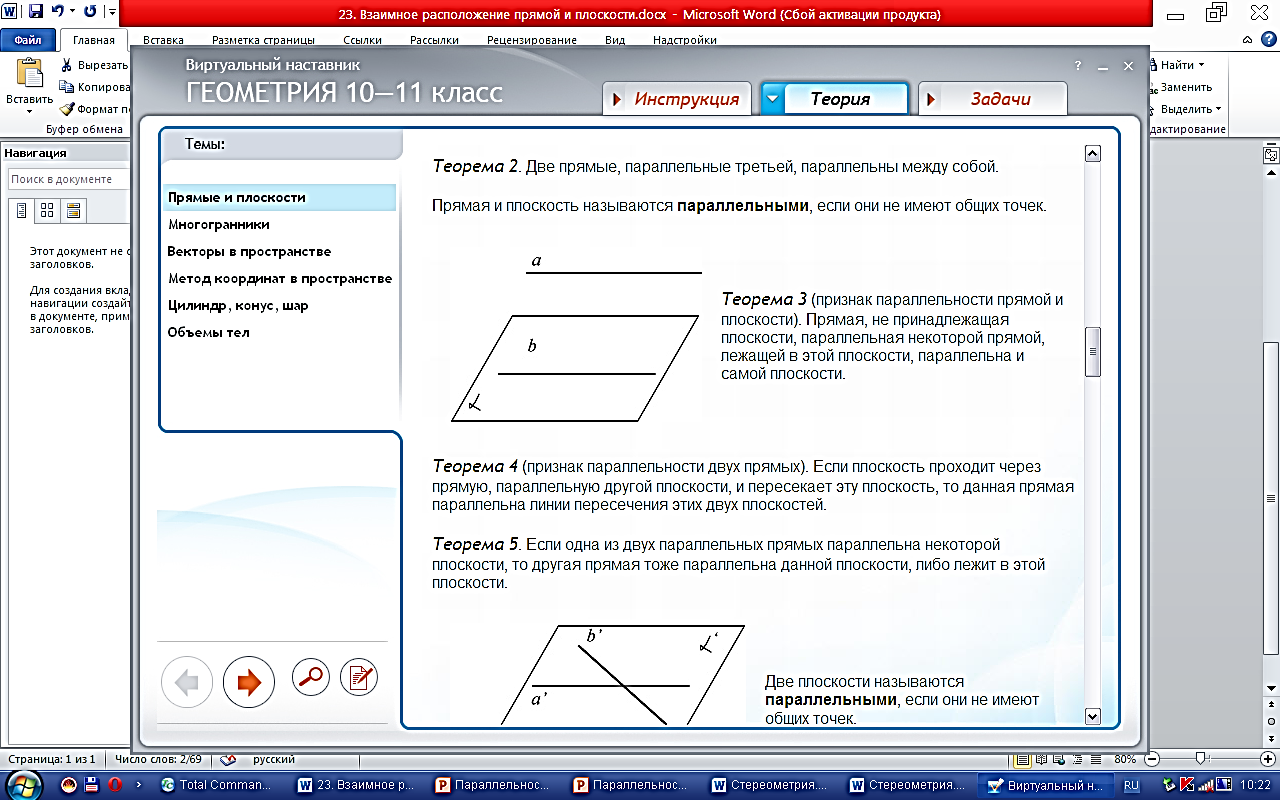
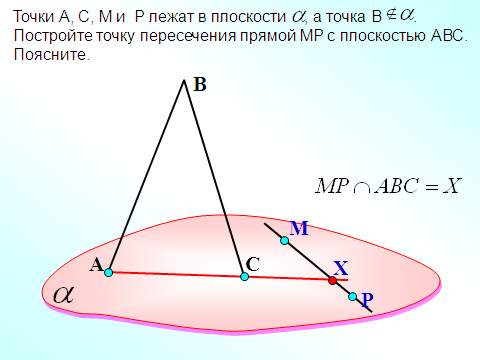
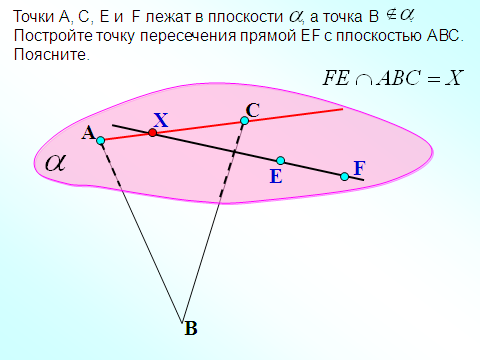
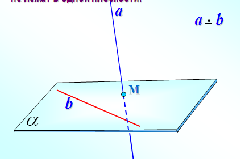
«23. Взаимное расположение прямой и плоскости»
Просмотр содержимого документа
«24. Скрещивающиеся и угол»
Просмотр содержимого документа
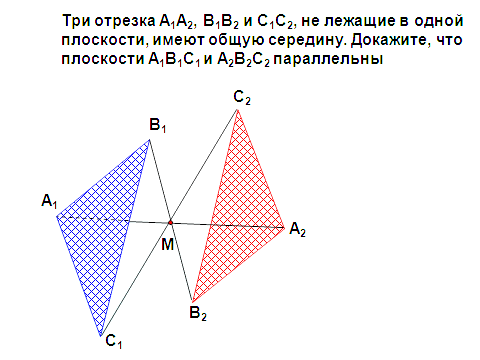
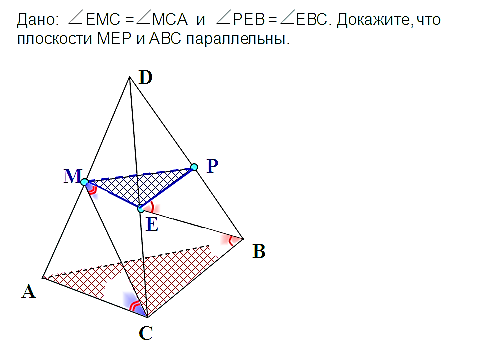
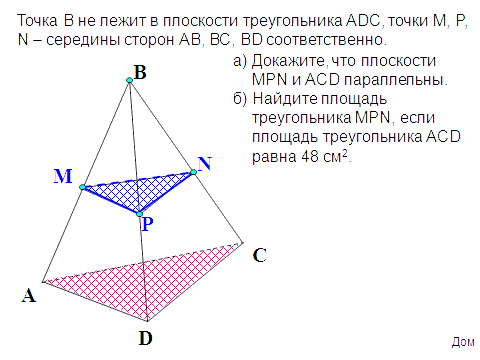
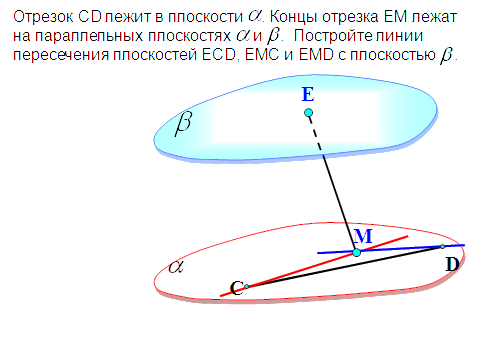
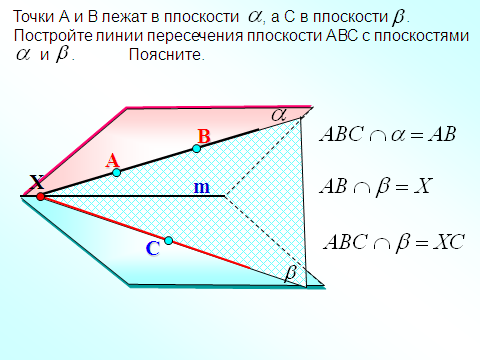
«25. параллельность плоскостей»
© 2021, Графова Татьяна Владимировна 2874 108




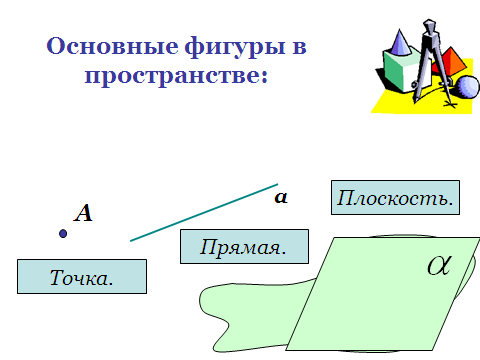
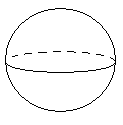
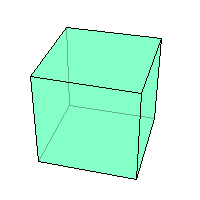
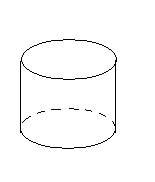 дним из простейших многогранников является куб (см. рис.1). Капли жидкости в невесомости принимают форму геометрического тела, называемого шаром (см. рис.2). Такую же форму имеет футбольный мяч. Консервная банка имеет форму геометрического тела, называемого цилиндром (см. рис. З).
дним из простейших многогранников является куб (см. рис.1). Капли жидкости в невесомости принимают форму геометрического тела, называемого шаром (см. рис.2). Такую же форму имеет футбольный мяч. Консервная банка имеет форму геометрического тела, называемого цилиндром (см. рис. З).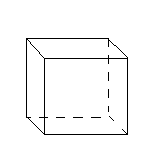
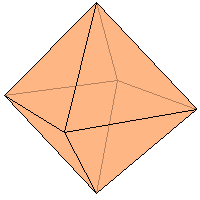
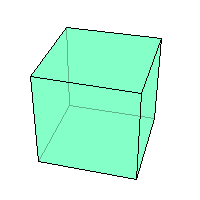
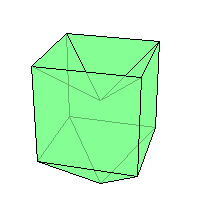 евыпуклый многогранник:
евыпуклый многогранник: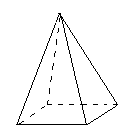
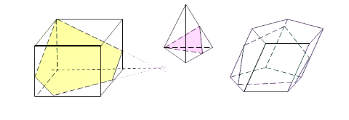
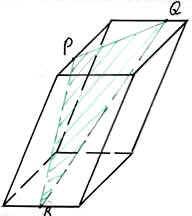
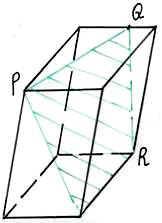
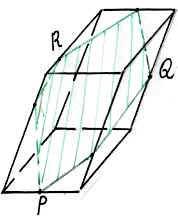
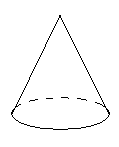 ри изучении пространственных фигур, в частности геометрических тел, пользуются их изображениями на чертеже. Как правило, изображением пространственной фигуры служит ее проекция на ту или иную плоскость. Одна и та же фигура допускает различные изображения. Обычно выбирается то из них, которое создает правильное представление о форме фигуры и наиболее удобное для исследования её свойств. На рисунках 4, 5, 6 изображены два многогранника - параллелепипед и пирамида, а так же фигура вращения – конус. При этом невидимые части этих фигур изображены штриховыми линиями.
ри изучении пространственных фигур, в частности геометрических тел, пользуются их изображениями на чертеже. Как правило, изображением пространственной фигуры служит ее проекция на ту или иную плоскость. Одна и та же фигура допускает различные изображения. Обычно выбирается то из них, которое создает правильное представление о форме фигуры и наиболее удобное для исследования её свойств. На рисунках 4, 5, 6 изображены два многогранника - параллелепипед и пирамида, а так же фигура вращения – конус. При этом невидимые части этих фигур изображены штриховыми линиями.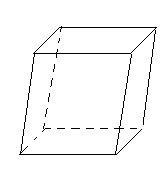
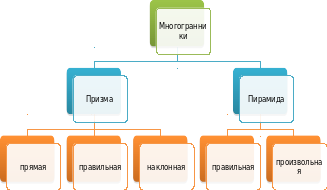
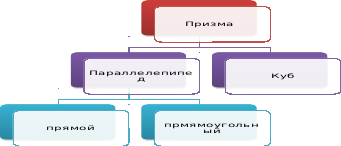
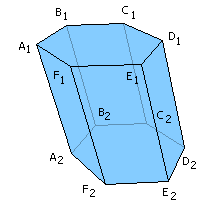
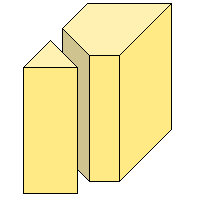 ризма
ризма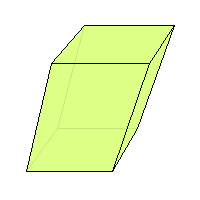
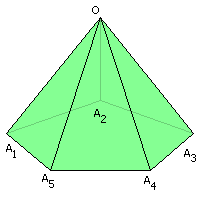 ятиугольная пирамида:
ятиугольная пирамида:
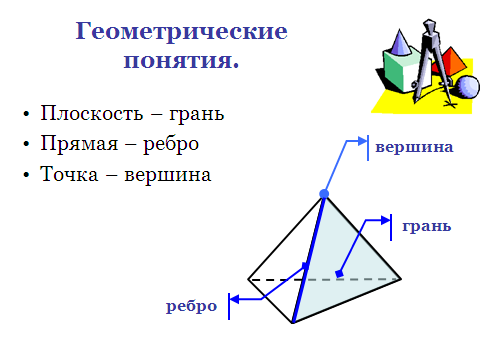
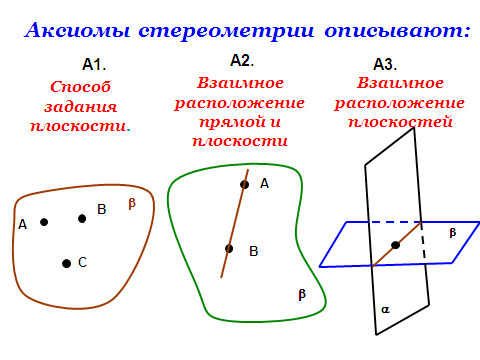
 редставление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.
редставление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.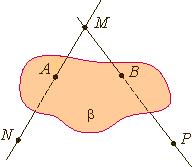

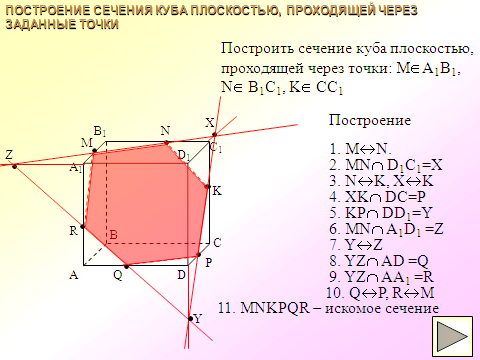

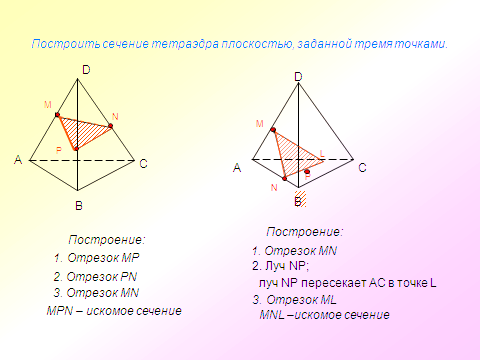
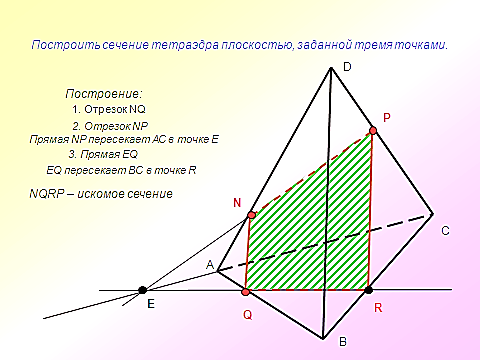
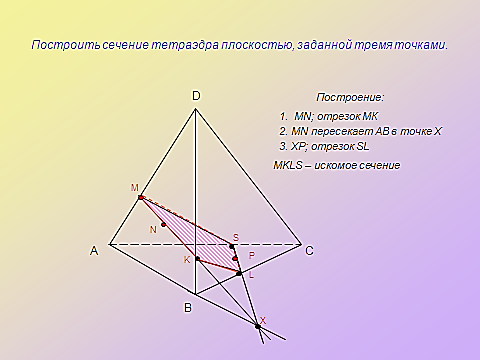
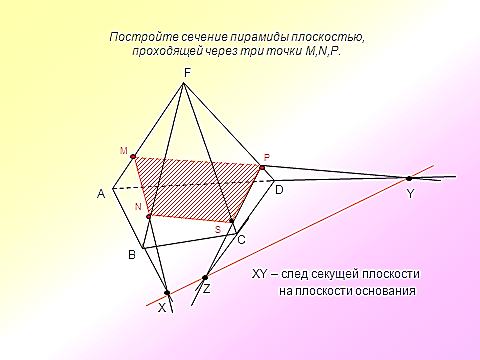
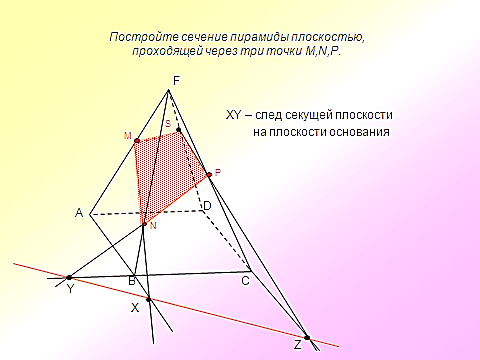
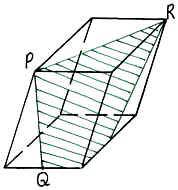
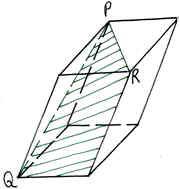
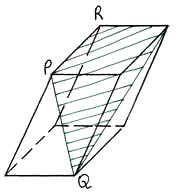
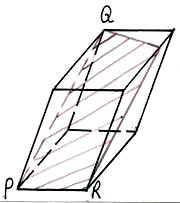
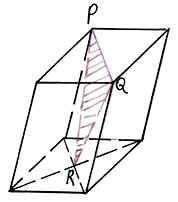
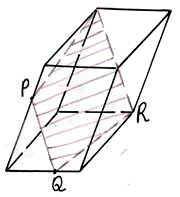
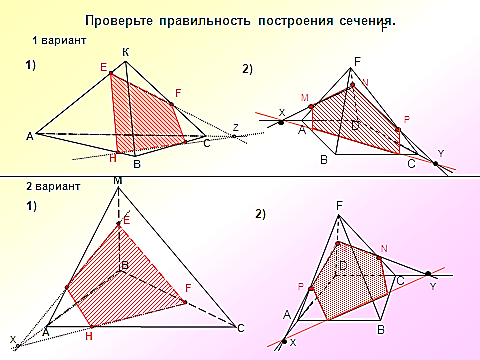
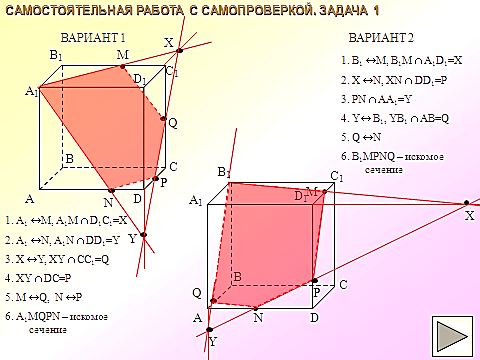 адача №1. Постройте сечение прямоугольного параллелепипеда, проходящее через точки А1, М, Р и
адача №1. Постройте сечение прямоугольного параллелепипеда, проходящее через точки А1, М, Р и 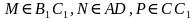
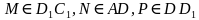
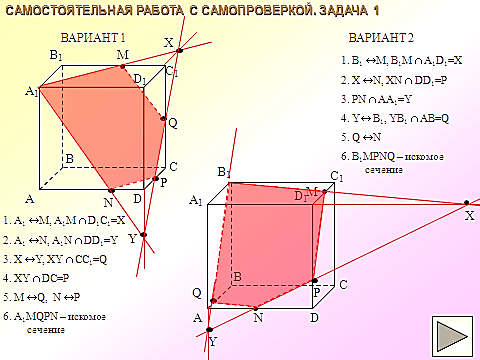 . X
. X 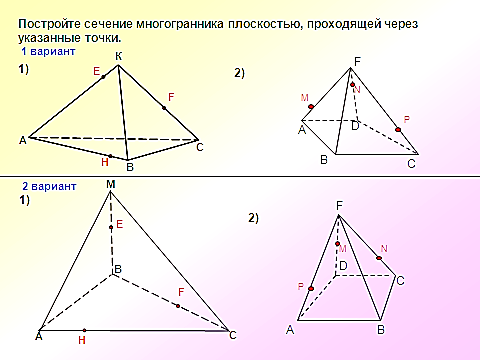

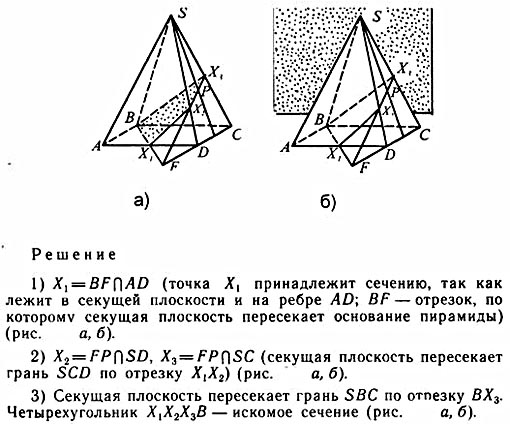

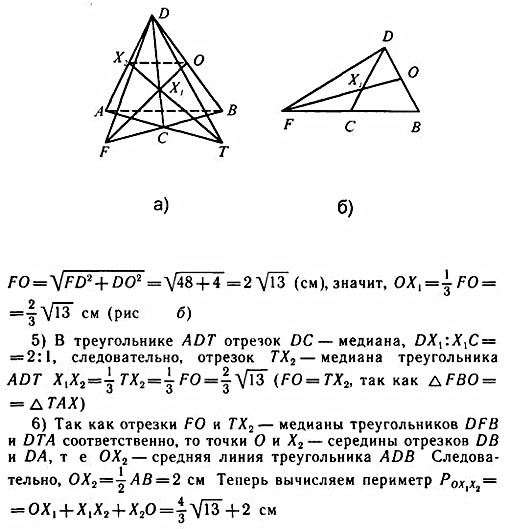

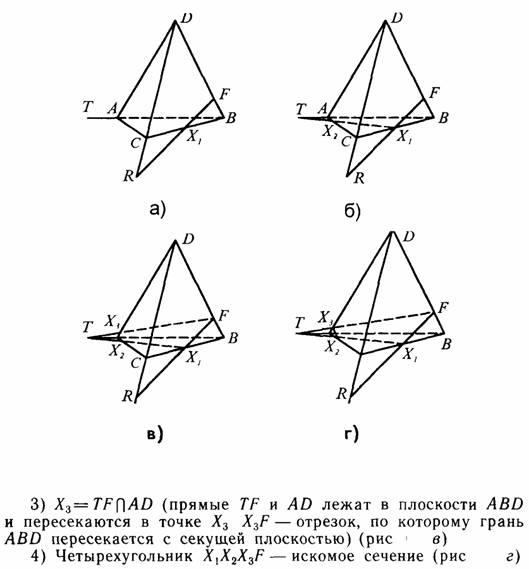

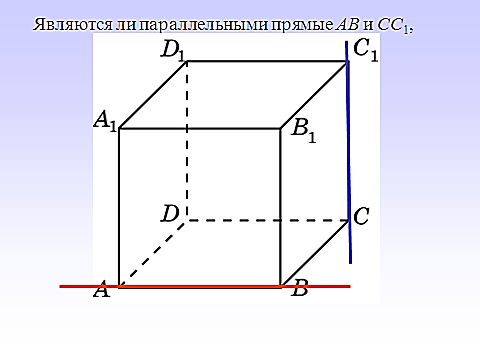
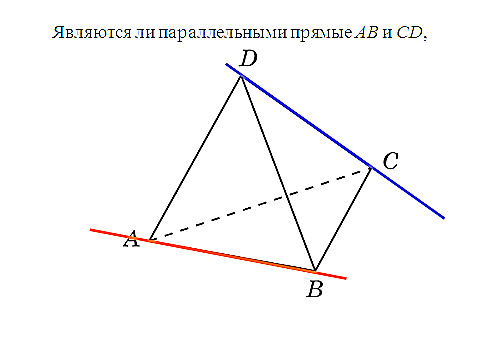
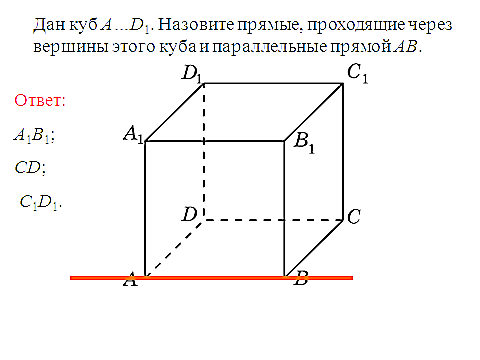
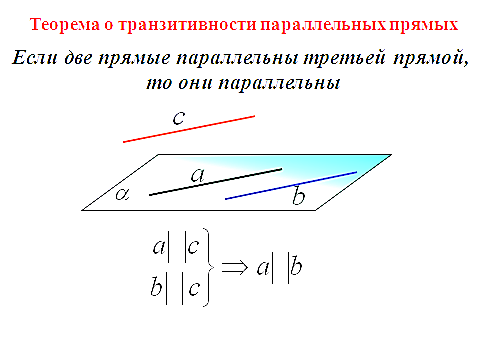

 ано:
ано: 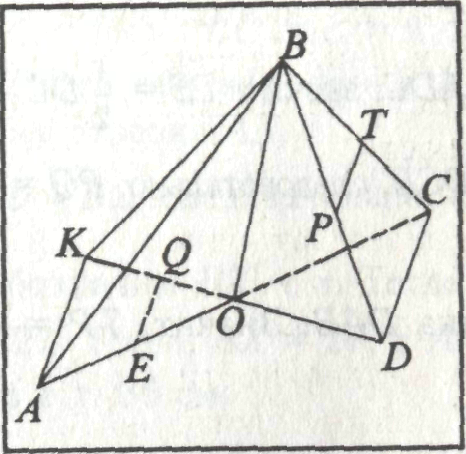 ано:
ано: 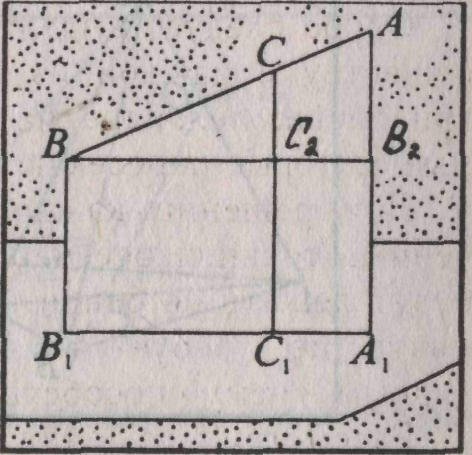 трезок АВ не пересекает плоскость α,
трезок АВ не пересекает плоскость α, 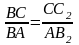
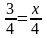 , следовательно х = 3, т.е. СС2 = 3см.
, следовательно х = 3, т.е. СС2 = 3см.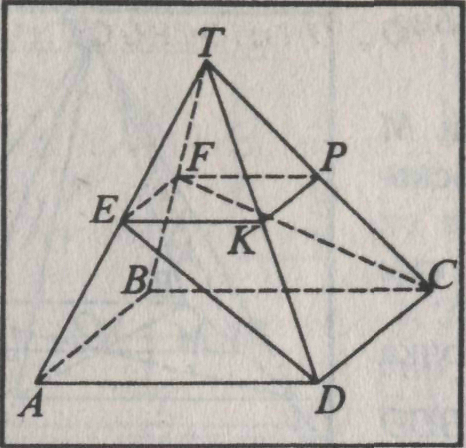 ано:
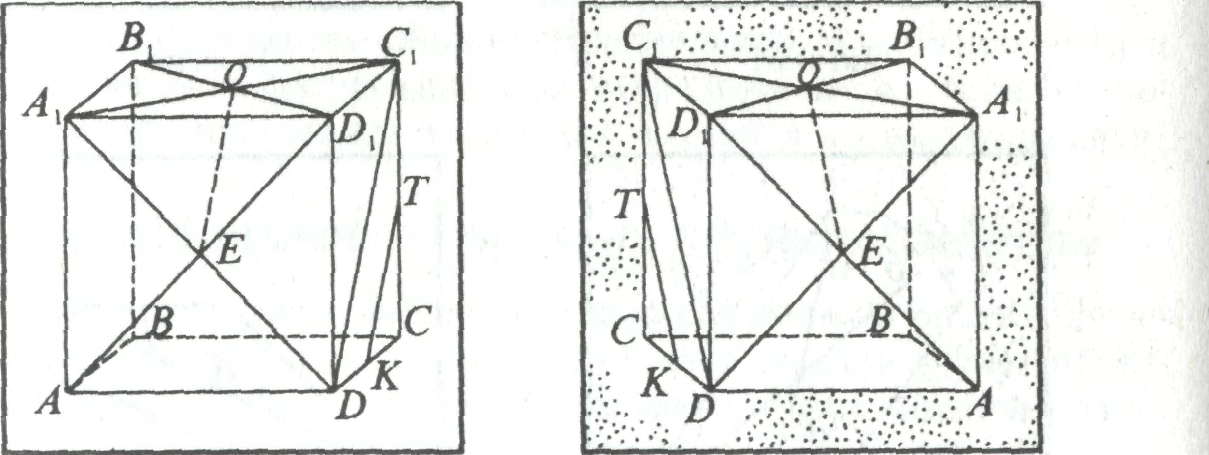
ано: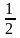 АВ =
АВ = 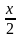 ;
; 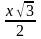 , как медианы правильных треугольников
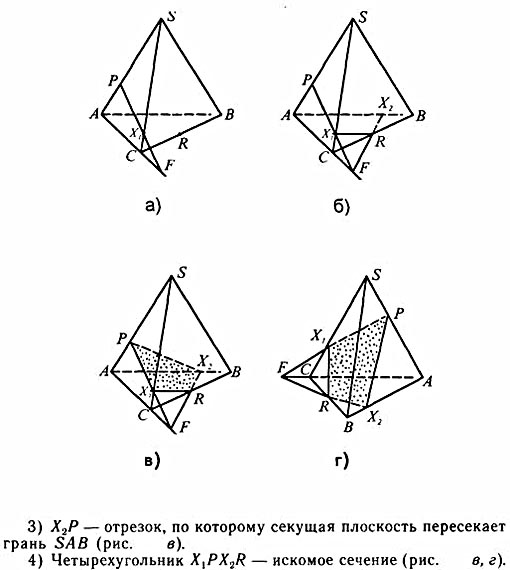
, как медианы правильных треугольников 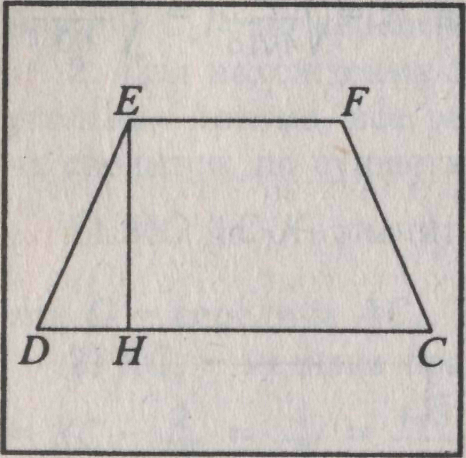 ) Сделаем выносной чертеж трапеции
) Сделаем выносной чертеж трапеции 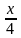 , где ЕН
, где ЕН 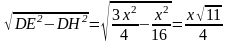
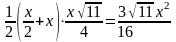
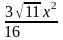
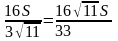
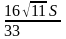
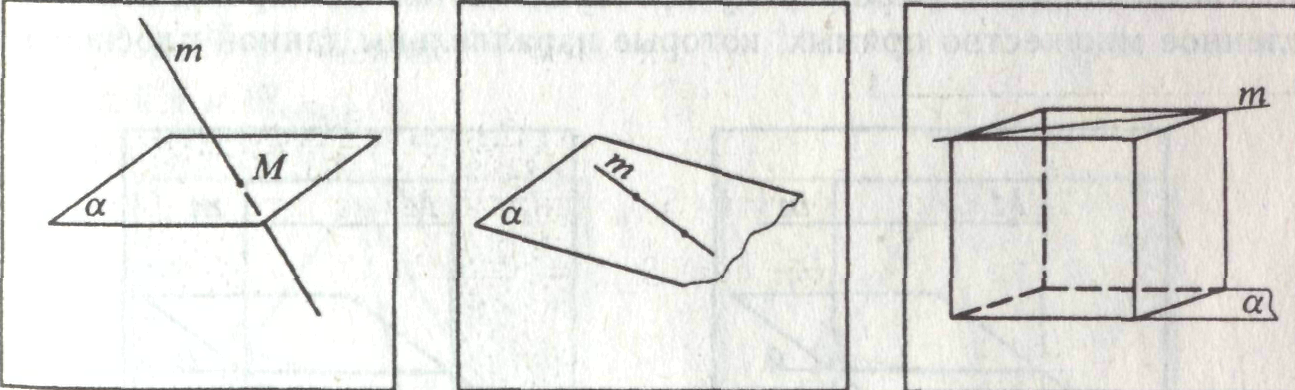
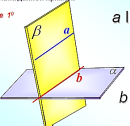
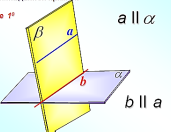
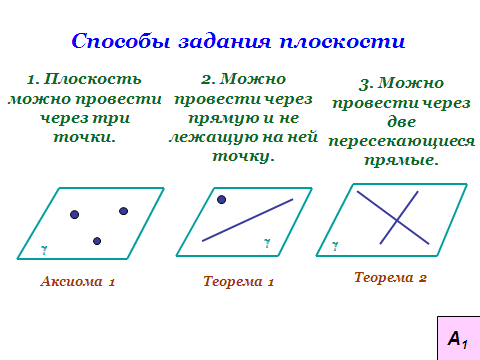
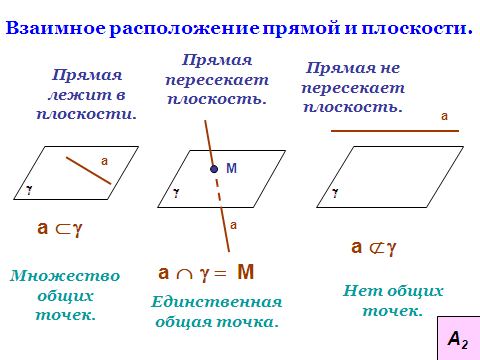
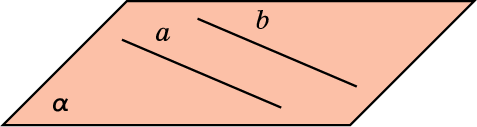
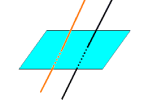
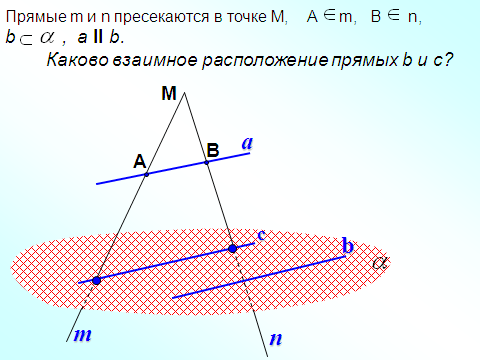
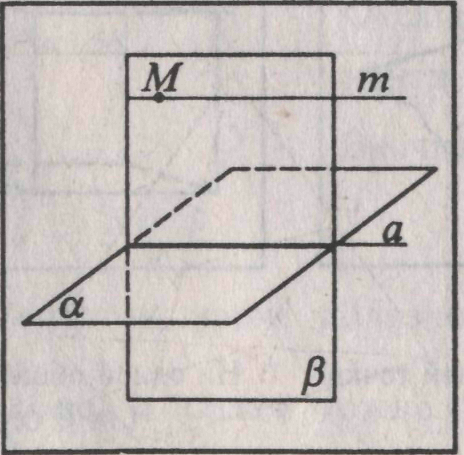 . Выберем произвольную прямую а в плоскости а.
. Выберем произвольную прямую а в плоскости а. 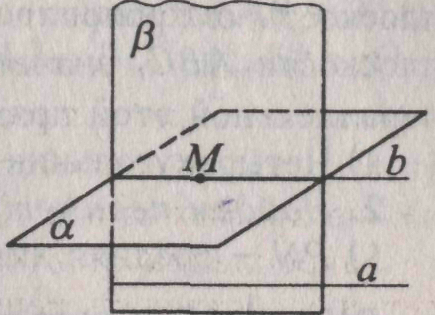 . Через точку М и прямую а проходит единственная плоскость β
. Через точку М и прямую а проходит единственная плоскость β 


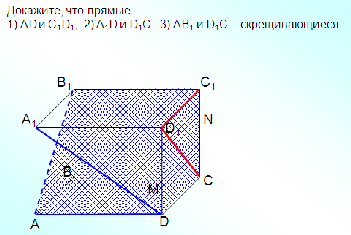
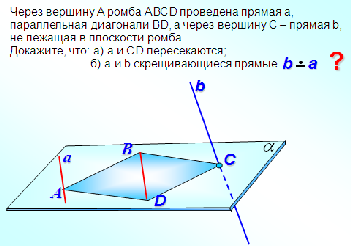
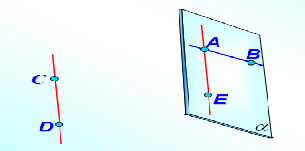
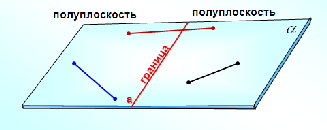
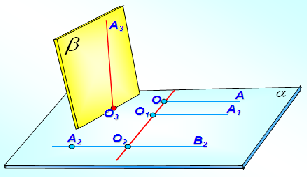
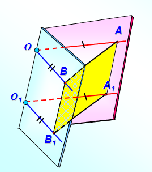
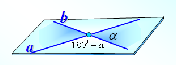
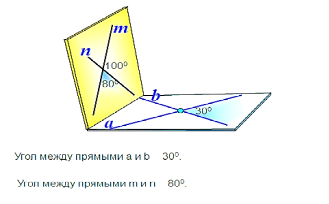
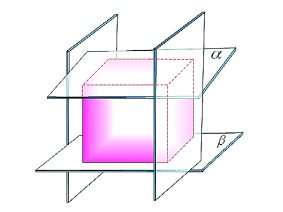
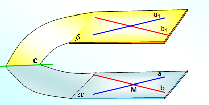
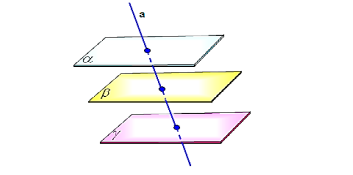
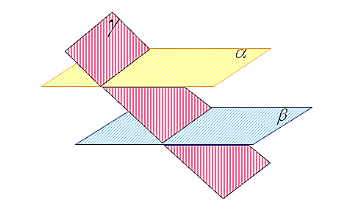
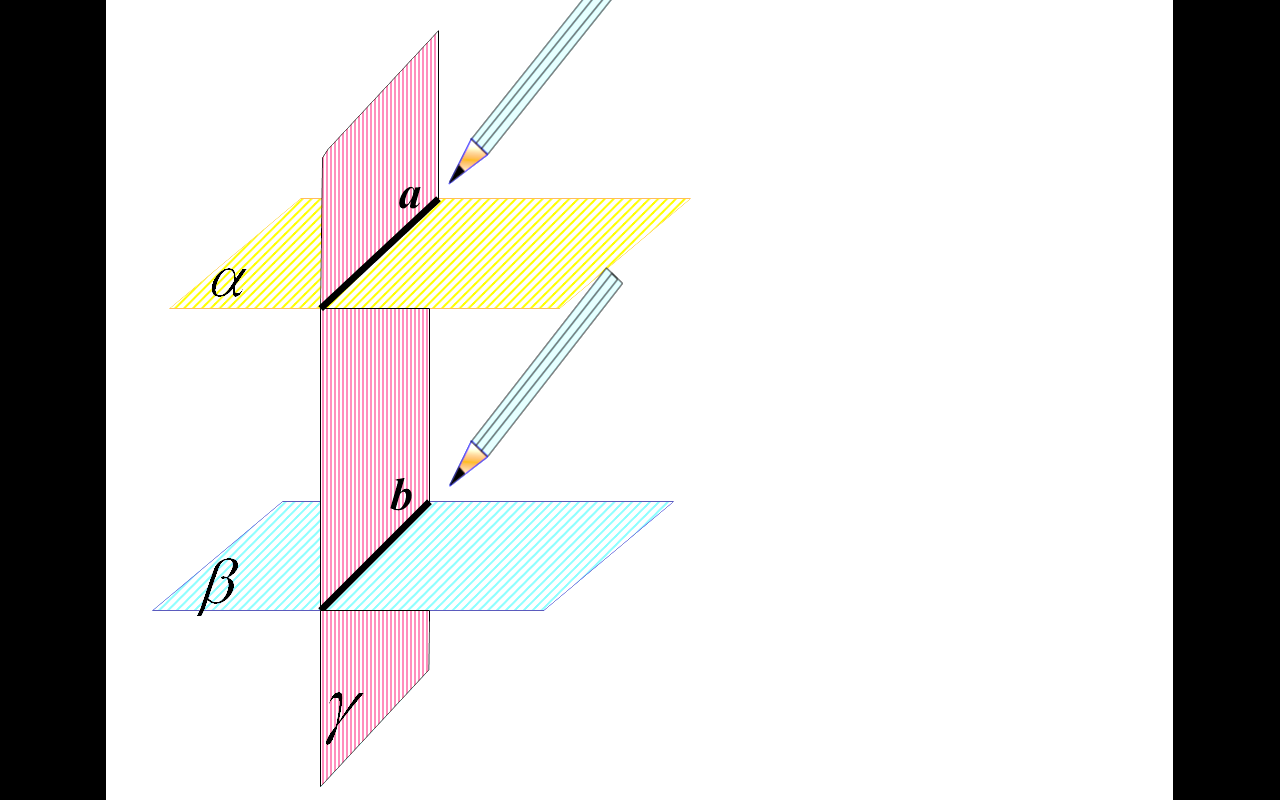
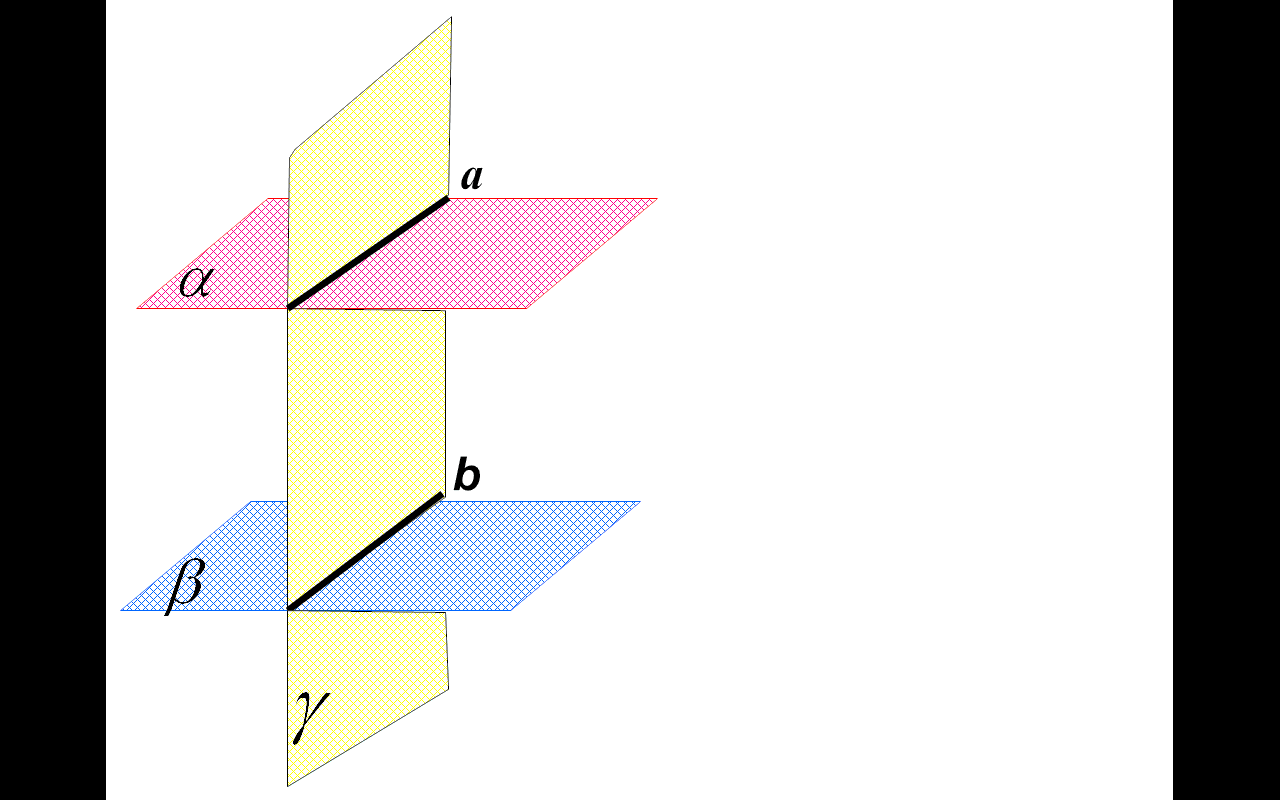
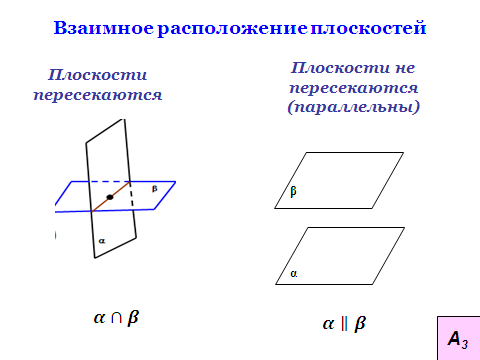
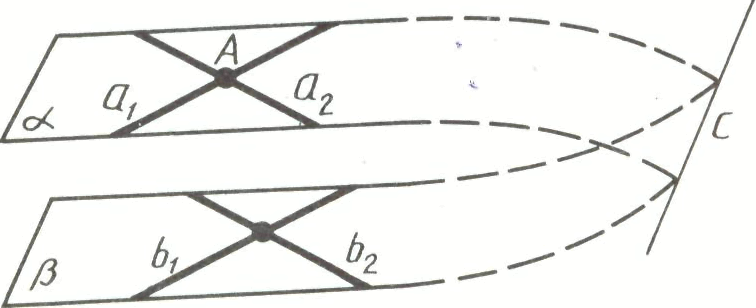 усть α и β — данные плоскости,
усть α и β — данные плоскости,