Бишкекский государственный
университет им. К. Карасаева
Абдалиева П.К.
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Сборник задач
Бишкек-2020
Абдалиева П.К.
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Для студентов экономических специальностей: сборник задач
Бишкек-2020
Абдалиева П.К.
Содержание
Введение…………………………………………………………….. 3
Элементы комбинаторики………………………………..
Кортежи. Прямые произведения…………….................
Размещения, перестановки, сочетания………………...
Число элементов и объединении множеств…………...
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ……………
Вариант 1…………………………………………………................
Вариант 2…………………………………………………................
Теория вероятностей и математическая
статистика ( обучающий модуль)……………………….
СЛУЧАЙНЫЕ СОБЫТИЯ…………………………………………
Алгебра событий……………………………………….
Классическая вероятность…………………………….
Относительная частота и статическая вероятность…
Геометрическая вероятность………………………….
Вероятность произведения событий……….................
Вероятность суммы совместных событий……………
Формула полной вероятности и формулы Бейеса…...
Классическая вероятность: типовые задачи…………
Повторение опытов. Формула Бернулли…………….
Предельные теоремы в системе Бернулли……………
Схема Бернулли: типовые задачи…………………….
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ……………
Вариант 1…………………………………………………................
Вариант 2…………………………………………………................
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ………………………………………
Ряд распределения дискретной случайной величины.
Числовые характеристики…………………………….
Функция распределения………………………………
Плотность распределения…………………………….
Случайные величины: типовые задачи………………
Специальные виды распределений……………………..
Нормальное распределение……………………………..
Типовые задачи на специальные распределения……...
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ……………...
Вариант 1…………………………………………………....................
Вариант 2…………………………………………………....................
Статическое распределение выборки………………….
Статические оценки параметров распределения……..
Математическая статистика: типовые задачи…………
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ………………
Вариант 1………………………………………………….....................
Вариант 2………………………………………………….....................
Комбинаторика ( контрольный модуль)………………….
Теоретическое упражнения……………………………..
Задания для итогового контроля……………………….
Теория вероятностей и математическая статистика
(контрольный модуль)………………………………………
СЛУЧАЙНЫЕ СОБЫТИЯ……………………………………………
Теоретические упражнения…………………………….
Задания для итогового контроля……………………….
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ ЭЛЕМЕНТЫ СТАТИСТИКИ……….
Теоретические упражнения…………………………….
Задания для итогового контроля……………………….
ЗАКЛЮЧЕНИЕ………………………………………………………
СПИСОК ЛИТЕРАТУРЫ…………………………………………..
ГЛОССАРИЙ…………………………………………………………
ПРИЛОЖЕНИЕ………………………………………………………
ВВЕДЕНИЕ
Начиная со второй половины прошлого века наблюдается всё более возрастающий интерес к теории вероятностей, математической статистике, теории случайных процессов и к применению вероятностно-статистических методов в самых разнообразных областях науки, техники, производства и экономики. Изучение различного рода случайных явлений, стохастических отклонений от нормы является важным средством предотвращения чрезвычайных ситуаций, техногенных катастроф, выпуска некачественной и ненадёжной продукции и т.п. С развитием современных средств вычислительной микропроцессорной техники расширяются возможности хранения, поиска и обработки больших массивов вероятностно-статистической информации о реальных объектах, выявления причинно-следственных связей между процессами и явлениями. Методы теории вероятностей и математической статистики находят всё большее применение, например, к анализу ошибок разного рода измерений, а также в физике, биологии, экологии, социологии, в телефонии и процессах обслуживания и т.д. Настоящее пособие представляет собой своеобразный курс теории вероятностей и математической статистики в задачах. На начальном этапе работы с книгой предполагается первичное ознакомление с основными понятиями (см. глоссарий). Следующий этап – обращение к обучающему модулю, в котором изложены основы комбинаторики, теории случайных событий и величин и начала математической статистики и в котором учебный материал иллюстрируется многочисленными примерами. Контрольный блок содержит теоретические упражнения, тренировочные задания, и проверочные задания двух типов: традиционного содержания в виде тестов со свободно конструируемыми ответами и подборку тестовых заданий, в которых предполагаются как выбор ответов (в том числе и свободный выбор), так и установление соответствий, и конструирование ответов. Результаты тестирования могут служить основанием для оценки уровня усвоения курса.
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
(ОБУЧАЮЩИЙ МОДУЛЬ)
1. Кортежи. Прямые произведения
1.1. Пусть даны множества G1, ..., Gn.
Кортежем длины n, составленным из элементов этих множеств, называется любая последовательность вида g = ( g1 ...,gn ),
Где gK ∈ Gk , 1≤k ≤n. Кортежи длины 2, т.е. кортежи вида ( g1, g2 ), называются упорядоченными парами;
кортежи длины 3 – упорядоченными тройками и т.д.
Декартовым произведением
G1 ×...×Gn множеств G1, ..., Gn, называется множество всех
G кортежей вида g= (g1 , ...gn, )
1.2.Пример. Брошены два игральных кубика. Найти количество всевозможных вариантов (всевозможных пар) очков на гранях.
Решение. Следует найти количество всех упорядоченных пар
( g1, g2 ), где gk – число очков, выпавших на k-й игрального кубика,
k = 1, 2 . Значение g1 – любое из чисел 1, 2, ..., 6 .
В паре с фиксированным (выбранным) g1 может оказаться любое g2 ∈ {1, 2, ..., 6}, т.е. таких пар будет 6, соответственно количеству возможных значений g2 . Учитывая, что выбор g1 возможен тоже шестью способами, имеем все упорядоченные пары в количестве 6⋅6 = 36 .
1.3. Обозначим через ν(M ) количество элементов конечного
множества М.
Теорема («принцип умножения»). Имеет место равенство
ν (G1 ×… ×Gn)= ν (G1)… ν (Gn)
В частности, если имеется k экземпляров одного и того же множества G и требуется найти число кортежей длины k, в которые входит по одному (и только одному) элементу из каждого экземпляра, то такие кортежи называются размещениями с повторениями; другими словами размещения с повторениями это кортежи вида )
g = ( g1 ...,gn ) ∈ G1 ×...×Gn
Число таких кортежей, согласно принципу умножения, очевидно, есть
v(Gk) = mk .
1.5. Пример. Какое максимальное число
шестизначных телефонных номеров может быть
в городской телефонной сети?
Решение. Имеем кортежи длины k = 6, в которых каждый элемент принадлежит множеству G = {0, 1, 2, ..., 9}, содержащему m = 10 элементов. Следовательно, число таких кортежей
v(G6) = 106 .
Однако телефонного номера, состоящего сплошь из нулей, обычно не бывает. Следовательно, искомое число номеров равно 106 – 1 = 999999.
2. Размещения, перестановки, сочетания
2.1. Если строить кортежи длины k из элементов одного и того же множества G так, чтобы элементы в кортеже не повторялись, то такие кортежи называются размещениями без повторений. Теорема. Количество размещений (из m элементов по k элементов) есть число
 = m(m-1) … (m-k+1)
= m(m-1) … (m-k+1)
Если использовать обозначение m!=1×2 … (m-1)m , считая 0! = 1! = 1, то легко проверить, что

2.2. В частности, размещения из m по т элементов называют перестановками; число всевозможных перестановок из m элементов есть
Pm = m!
Пример. Сколькими способами можно разложить в ряд на витрине магазина пять DVD-дисков?
Решение. Имеем кортежи длиной в пять элементов, составленные из элементов множества G, для которого
ν (G) = 5
Следовательно, ищем количество перестановок из пяти элементов
P5 = 5! = 120.
2.4 .Пример. Сколькими способами можно расставить на
полке шесть книг, если?
две определённые книги должны всегда стоять рядом;
эти две книги не должны стоять рядом?
Решение. а) Пару книг, которые должны стоять рядом, условимся пока рассматривать как одну книгу. Тогда нужно расставить пять книг по пяти местам, что можно сделать P5 = 5! способами. Учитывая теперь порядок расположения тех двух книг, которые мы посчитали за одну, имеем P2 перестановок между ними. Согласно принципу умножения, получаем окончательно число способов
P5 × P2 = 120 × 2 = 240.
б) Способов переставить шесть книг существует Р6 = 720, но из них, как установлено в п. а) существует 240 способов поставить определённые книги вместе. Следовательно, число способов поставить книги так, чтобы две заданные книги рядом не стояли, равно разности 720 – 240 = 480.
Пример. На заседании Думы из шести возможных кандидатов выбирают председателя комитета, его первого и второго заместителя. Сколько существует способов формирования руководящего состава этого комитета?
Решение. Имеем кортежи длиной в три элемента (упорядоченные тройки), составленные из элементов множества G, для которого
ν (G) = 6
Следовательно, ищем количество размещений  :
:
 =
=  =
=  =120
=120
Если теперь строить из элементов множества G, для которого
ν (G) = m,
неупорядоченные подмножества по k элементов, то такие подмножества называют сочетаниями из m по k элементов. Теорема. Количество всевозможных сочетаний из m по k элементов может быть вычислено по формуле
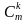 =
= 
Имеют место равенства:
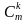 =
=  (2.1)
(2.1)
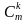 =
= 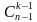 -
-  (2.2)
(2.2)
 +
+ 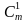 + … +
+ … +  = 2m (2.3)
= 2m (2.3)
Пример. Имеется 10 различных игрушек, из которых
формируют комплекты подарков по три игрушки в
каждом. Сколько таких различных комплектов можно
сформировать?
Решение. Имеем всевозможные неупорядоченные подмножества по три элемента из 10. Ищем количество сочетаний, т.е.
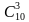 =
=  =
=  = 120
= 120
Итак, можно сформировать 120 различных комплектов подарков.
2.9. Пример. Найти n из уравнения 1 15 1 23 15 = C nCC n n n n + − − ++ . Решение. Воспользовавшись формулой (2.2), запишем уравнение в виде
14!1! 15!
15=
1)!2(1)!( 2)!(
)!3(! 3)!(
⋅
+
+−+⋅− +
−
−+⋅ +
n
nnn n
nnn n
или
.1)15(=
3!1)!( 2)1)((1)!(
3!! 3)2)(1)((!
+
⋅− ++⋅−
−
⋅ +++⋅
n
n nnnn
n nnnn
Сокращая дроби и сокращая обе части уравнения на 1 +n (что можно делать, так как n 0), имеем
(n + 2)(n + 3) – n(n + 2) = 3! 15⋅ , откуда n + 2 = 30, т.е. n = 28.
2.10. Размещения, перестановки, сочетания можно интерпретировать как всевозможные выбор
Задачи по комбинаторике с решениями онлайн
Задача 1. У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней подряд она выдает по одному фрукту. Сколькими способами это может быть сделано?
Решение задачи о выдаче фруктов
Задача 2. Предприятие может предоставить работу по одной специальности 4 женщинами, по другой - 6 мужчинам, по третьей - 3 работникам независимо от пола. Сколькими способами можно заполнить вакантные места, если имеются 14 претендентов: 6 женщин и 8 мужчин?
Решение задачи о работниках
Задача 3. В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человека, при условии, что все они должны ехать в различных вагонах?
Решение задачи по комбинаторике о пассажирах
Задача 4. В группе 9 человек. Сколько можно образовать разных подгрупп при условии, что в подгруппу входит не менее 2 человек?
Решение задачи о подгруппах
Задача 5. Группу из 20 студентов нужно разделить на 3 бригады, причем в первую бригаду должны входить 3 человека, во вторую — 5 и в третью — 12. Сколькими способами это можно сделать.
Решение задачи по комбинаторике о бригадах
Задача 6. Для участия в команде тренер отбирает 5 мальчиков из 10. Сколькими способами он может сформировать команду, если 2 определенных мальчика должны войти в команду?
Решение о командах
Задача 7. В шахматном турнире принимали участие 15 шахматистов, причем каждый из них сыграл только одну партию с каждым из остальных. Сколько всего партий было сыграно в этом турнире?
Задача о шахматном турнире с решением
Задача 8. Сколько различных дробей можно составить из чисел 3, 5, 7, 11, 13, 17 так, чтобы в каждую дробь входили 2 различных числа? Сколько среди них будет правильных дробей?
Задача по комбинаторике с решением
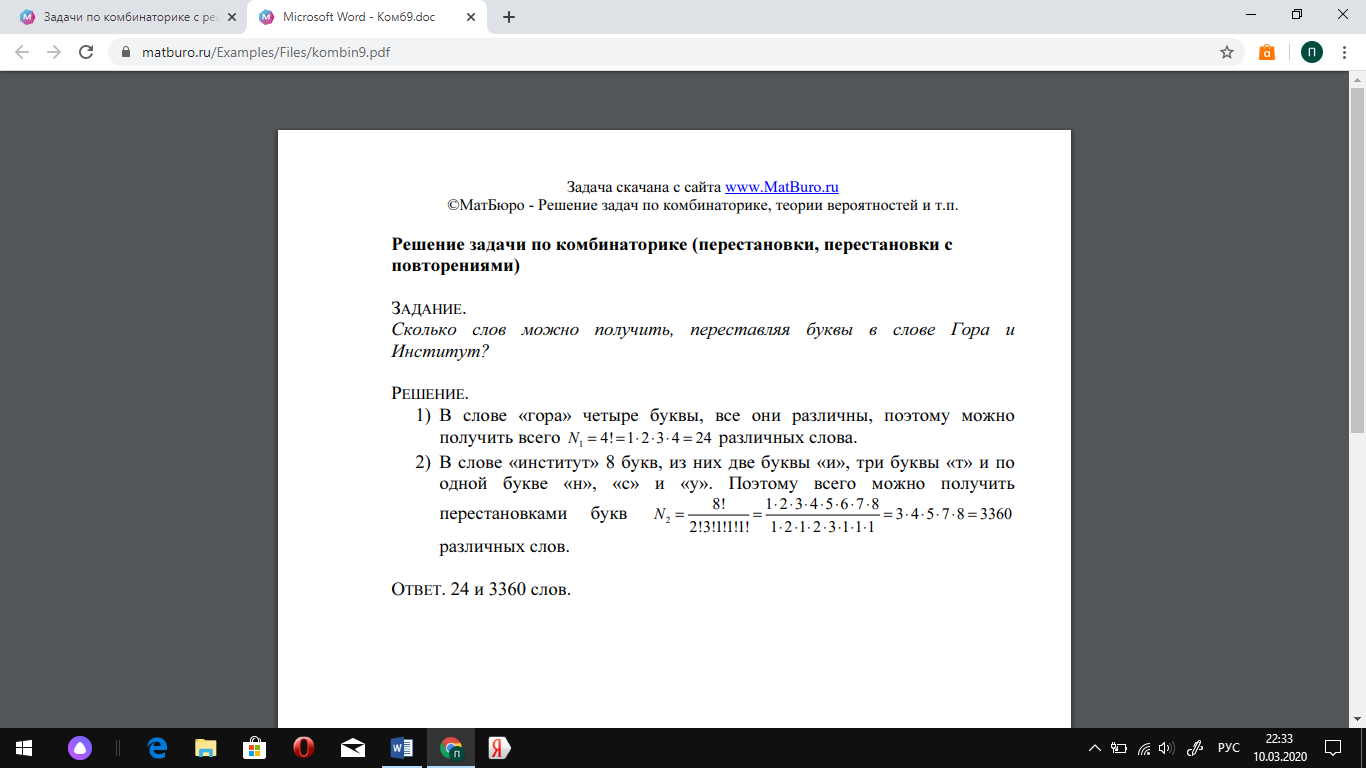
Задача 9. Сколько слов можно получить, переставляя буквы в слове Гора и Институт?
Задача по комбинаторике о перестановке букв
Задача 10. Каких чисел от 1 до 1 000 000 больше: тех, в записи которых встречается единица, или тех, в которых она не встречается?
Задача по комбинаторике с решением
№1Тема: Комбинаторика Задание. У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней подряд она выдает по одному фрукту. Сколькими способами это может быть сделано? Решение. Имеем набор {я, я, г, г, г}. Всего перестановок пятиэлементного множества 5!, но мы не должны учитывать перестановки, в которых объекты одного типа меняются местами несколько раз, поэтому нужно поделить на возможное число таких перестановок: 2! · 3!. Получаем в итоге 5! 2! · 3! = 3 · 4 · 5 2 · 3 = 10. Ответ: 10 способов.
№2Тема: Комбинаторика Задание. Предприятие может предоставить работу по одной специальности 4 женщинами, по другой - 6 мужчинам, по третьей - 3 работникам независимо от пола. Сколькими способами можно заполнить вакантные места, если имеются 14 претендентов: 6 женщин и 8 мужчин? Решение. Имеем 14 претендентов и 13 рабочих мест. Сначала выберем работников на первую специальность, то есть 4 женщин из 6: C4 6 = 6! 4! · 2! = 15. Далее независимо аналогичным образом выберем мужчин на вторую специальность: C6 8 = 8! 6! · 2! = 28. Осталось 2 женщины, 2 мужчин и 3 вакантных места, которые, по условию, могут занять любые из четырех оставшихся человек. Это может быть сделано 2 вариантами: 1. 1 женщина и 2 мужчин (выбираем женщину C1 2 = 2 способами) 2. 1 мужчина и 2 женщины (выбираем мужчину C1 2 = 2 способами). В итого получаем 15 · 28(2 + 2) = 1680 способов. Ответ: 1680 способов.
№3 Решение задачи по комбинаторике (размещения) ЗАДАНИЕ. В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человека, при условии, что все они должны ехать в различных вагонах? РЕШЕНИЕ. Т.к. все пассажиры должны ехать в разных вагонах, требуется отобрать 4 вагона из 9 с учетом порядка (вагоны отличаются №), эти выборки – размещения из n различных элементов по m элементов, где n=9, m=4. Число таких размещений находим по формуле: A = n ⋅(n − ⋅()1 n − ⋅...)2 ⋅(n − m + )1 m n . Получаем: 9 8 7 6 3024 4 A9 = ⋅⋅⋅ = . ОТВЕТ. 3024 способами можно рассадить в поезде 4 человека.
№4 Решение задачи по комбинаторике (правило сложения, сочетания) ЗАДАНИЕ. В группе 9 человек. Сколько можно образовать разных подгрупп при условии, что в подгруппу входит не менее 2 человек? РЕШЕНИЕ. Не менее 2-х человек, т.е 2+7 или 3+6 или 4+5 человек (5+4, 6+3, 7+2 – те же самые комбинации). В каждой выборке важен только состав, т.к. члены подгруппы не различаются по ролям, т.е. выборки − сочетания из n различных элементов по m элементов, их число: (! !) ! m n m n C m n ⋅ − = , где n!= 1⋅ 2 ⋅3⋅...⋅ n . Число выборок из 2-х человек: 36 1 2 8 9 !7!2 !9 9(!2 !)2 2 !9 9 = ⋅ ⋅ = ⋅ = ⋅ − C = . Число выборок из 3-х человек: 84 1 2 3 7 8 9 !6!3 !9 9(!3 !)3 3 !9 9 = ⋅⋅ ⋅ ⋅ = ⋅ = ⋅ − C = . Число выборок из 4-х человек: 126 1 2 3 4 6 7 8 9 !5!4 !9 9(!4 !)4 4 !9 9 = ⋅⋅⋅ ⋅ ⋅ ⋅ = ⋅ = ⋅ − C = . Применяем правило сложения: 36 84 126 246 4 9 3 9 2 C9 + C + C = + + = способов ОТВЕТ. 246 способов.
№5 Решение задачи по комбинаторике (сочетания, правило произведения)
ЗАДАНИЕ. Группу из 20 студентов нужно разделить на 3 бригады, причем в
первую бригаду должны входить 3 человека, во вторую — 5 и в третью —
12. Сколькими способами это можно сделать.
РЕШЕНИЕ.
Создавая первую бригаду, отбирают 3 человека из 20, создавая вторую – 5 из
оставшихся 17, создавая третью – 12 из оставшихся 12. Для выборок важен
только состав (роли членов бригады не различаются).
Эти выборки - сочетания из n различных элементов по m элементов, их
число:
(! !)
!
m n m
n
C
m
n
⋅ −
= .
Создавая сложную выборку (из 3-х бригад), воспользуемся правилом
умножения:
3 5 12
20 17 12
20! 17! 12! 20! 17! 12!
3! (20 3)! 5! (17 5)! 12! (12 12)! 3! 17! 5! 12! 12! 0!
13 14 15 16 17 18 19 20 7054320.
1 2 3 1 2 3 4 5
N C= ⋅ ⋅ = ⋅ ⋅ = ⋅ ⋅ = С С
⋅ − ⋅ − ⋅ − ⋅ ⋅ ⋅
⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅
= =
⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅
ОТВЕТ. 7054320 способов.
№6 Решение задачи по комбинаторике (сочетания) ЗАДАНИЕ. Для участия в команде тренер отбирает 5 мальчиков из 10. Сколькими способами он может сформировать команду, если 2 определенных мальчика должны войти в команду? РЕШЕНИЕ. Т.к. известно, что двое мальчиков войдут в команду, то остается отобрать 3 из 8. Для выборки важен только состав (по условию все члены команды не различаются по ролям). Следовательно, выборки – сочетания из n различных элементов по m элементов, их число: (! !) ! m n m n C m n ⋅ − = , где n!= 1⋅ 2 ⋅3⋅...⋅ n , при n=8, m=3. 56 1 2 3 6 7 8 !5!3 !8 8(!3 !)3 3 !8 8 = ⋅⋅ ⋅ ⋅ = ⋅ = ⋅ − C = . ОТВЕТ. 56 способов сформировать команду
№7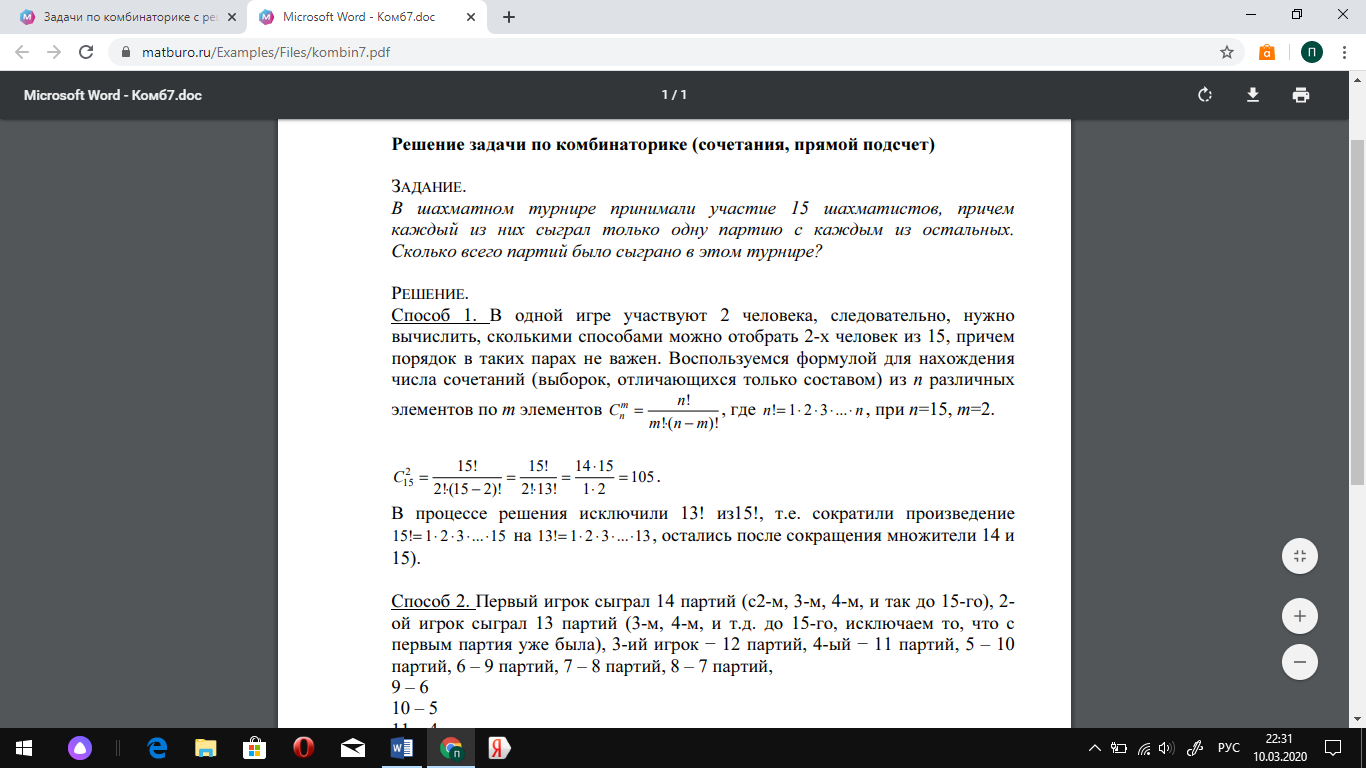
 №9
№9
№8









 = m(m-1) … (m-k+1)
= m(m-1) … (m-k+1)
 :
: =
=  =120
=120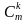 =
= 
 (2.1)
(2.1)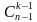 -
-  (2.2)
(2.2) +
+ 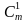 + … +
+ … +  = 2m (2.3)
= 2m (2.3)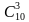 =
=  =
=  = 120
= 120
 №9
№9


















