Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №1 г. Нижний Ломов
имени Тархова Сергея Федоровича
Традиционный XVII Кикинский форум «Одаренные дети»
Информационно - исследовательский проект
«Метод интервалов на тригонометрической окружности»
Автор: Безбородова Анна,
ученица 10 «Б» класса
МБОУ СОШ №1
г. Нижний Ломов им. С.Ф.Тархова
Руководитель:
Бихтякова Галина Петровна,
учитель математики
МБОУ СОШ №1 г. Нижний Ломов им. С.Ф.Тархова
г. Нижний Ломов
2019г.
Слайд 1
В школьном курсе геометрии в 10 классе рассматриваются простейшие тригонометрические неравенства и неравенства, сводящиеся к ним, решаемые с помощью единичной окружности. При решении неравенств этим способом возникают ошибки при записи промежутков и в выборе границ. Я считаю, что их можно избежать, если научиться решать тригонометрические неравенства несколькими способами, в частности методом интервалов. Тема моего проекта «Метод интервалов на тригонометрической окружности»
Слайд 2
«Лучший способ изучить что-либо - это открыть самому» (Д. Пойя).
Слайд 3
Меня заинтересовал вопрос о способах решения более сложных тригонометрических неравенств.
Оказалось, что применение метода интервалов значительно украшает решение тригонометрических неравенств.
Слайд 4
Результаты работы над проектом помогут одноклассникам успешней
подготовиться к ЕГЭ
Слайд 5
Цель исследования
Изучить применение алгоритма метода интервалов при решении различных тригонометрических неравенств, в том числе в нестандартных ситуациях.
Задачи
- обобщить алгоритм метода интервалов для применения его к решению различных неравенств;
- отобрать материал для решения тригонометрических неравенств;
- создать презентацию исследования.
Слайд 6
Объектом изучения данной темы является практическая направленность школьного курса математики.
Вид проекта – информационно-исследовательский
Целевая аудитория
Проект направлен на аудиторию учащихся 10, 11 классов.
Слайд 7
Выбранные методики:
- изучение имеющейся литературы;
- получение фактических данных путем решения задач;
- анализ и классификация информации;
- сравнение, обобщение;
- изучение литературных и интернет - ресурсов;
- оформление полученных выводов.
Слайд 8
Практическая значимость проекта
В результате работы над проектом, я научилась сама и научила одноклассников решать тригонометрические неравенства методом интервалов на тригонометрической окружности.
Перспективы развития проекта
В следующем учебном году планирую познакомить с результатами проекта учащихся 11 классов.
Слайд 9
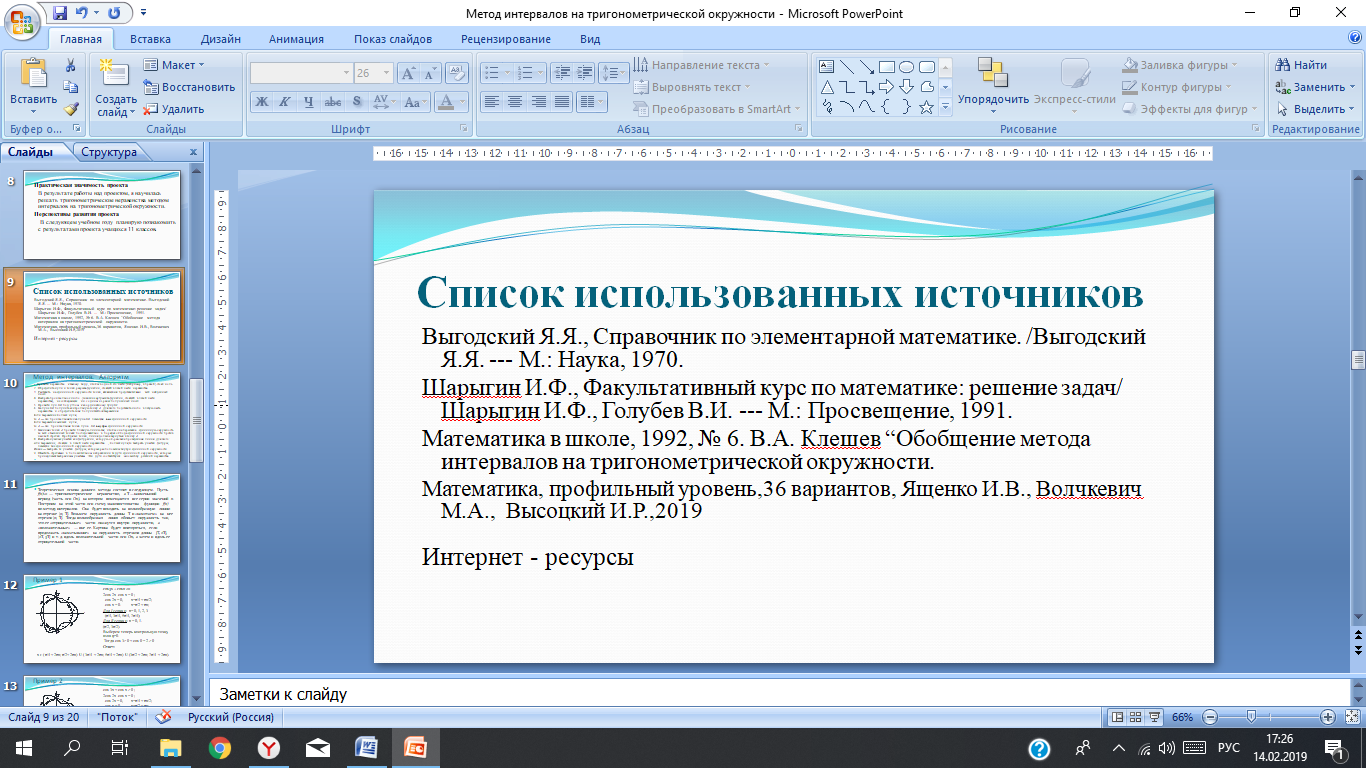
Слайд 10
Метод интервалов основан на свойстве непрерывных функций. Одним из важных свойств является свойство знакопостоянства непрерывной функции: если на интервале (a;b) функция f непрерывна и не обращается в 0, то она на этом интервале сохраняет постоянный знак.
При решении тригонометрических неравенств методом интервалов я следовала алгоритму:
1. Привести неравенство к такому виду, чтобы в одной его части (например, в правой) стоял нуль.
2. Определить нули и точки разрыва функции, стоящей в левой части неравенства.
3. Расставить на единичной окружности точки, являющиеся представителями всех найденных чисел.
4. Выбрать произвольное число (значение аргумента функции, стоящей в левой части неравенства), не совпадающее ни с одним из ранее полученных чисел.
5. Провести луч ОA под углом к координатному лучу Ох.
6. На луче ОA получить контрольную точку A. Для этого подставить число в левую часть неравенства и определить знак получившегося выражения.
Если выражение больше нуля, то A — это произвольная точка луча ОA, лежащая вне единичной окружности.
Если выражение меньше нуля, то A — это произвольная точка луча ОA внутри единичной окружности.
7. Начиная с точки A провести плавную линию так, чтобы она пересекала единичную окружность во всех отмеченных точках последовательно в порядке обхода единичной окружности против часовой стрелки. Пройдя все точки, линия должна вернуться в точку A.
8. Выбрать нужные участки конфигурации, которую образовала проведенная линия. Для этого:
если выражение, стоящее в левой части неравенства, больше нуля, то выбрать участки фигуры, лежащие вне единичной окружности.
Иначе — выбрать те участки фигуры, которые расположены внутри единичной окружности.
9. Отметить стрелками в положительном направлении те дуги единичной окружности, которые принадлежат выбранным участкам. Эти дуги соответствуют множеству решений неравенства.
Слайд 11
Теоретическая основа данного метода состоит в следующем. Пусть f(х)0 — тригонометрическое неравенство, а T —наименьший период (часть оси Ох), на котором помещаются все серии значений x. Построим на этой части оси схему знакопостоянства функции f(х) по методу интервалов. Она будет походить на волнообразную линию на отрезке [0; T]. Возьмем окружность длины T и «намотаем» на нее отрезок [0; T]. Тогда волнообразная линия обовьет окружность так, что ее «отрицательные» части окажутся внутри окружности, а «положительные» - вне ее. Картина будет повторяться, если продолжать «наматывание» на окружность отрезков длины [Т, 2T], [2T, 3T] и т. д. вдоль положительной части оси Ох, а затем и вдоль ее отрицательной части.
Слайд 12
Проиллюстрируем описанный способ.
Пример № 1. Решить неравенство cos3x + cosх
Решение:
Приведем левую часть неравенства к виду 2 cos 2х соsх и рассмотрим уравнение 2cos2хсоsх=0, которое равносильно совокупности уравнений:
cos2х =0 или соsх=0
Первое из уравнений этой совокупности дает I серию значений х:  Второе из уравнений cовокупности приводит ко II серии:
Второе из уравнений cовокупности приводит ко II серии: 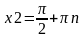 .
.
Заполним теперь единичную окружность соответствующими точками. Для I серии достаточно взять n= 0, 1, 2, 3. Тогда значения х1 соответственно равны 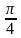 ,
,  ,
, 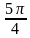 ,
, (при остальных значениях n точки будут повторяться). Значения из серии x2 на единичной окружности можно представить точками
(при остальных значениях n точки будут повторяться). Значения из серии x2 на единичной окружности можно представить точками 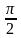 и
и  , которые получены при n = 0 и n= 1.
, которые получены при n = 0 и n= 1.
Выберем теперь контрольную точку, положив  =0. Тогда cos0 +соs0= 2.
=0. Тогда cos0 +соs0= 2.
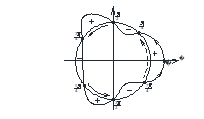
Значит, в данном случае луч ОA совпадает с координатным лучом Ох (угол между ними равен 0). Выберем на луче Оx произвольную точку A, находящуюся внe единичной окружности.
Соединяем точку A со всеми отмеченными точками на единичной окружности так, как показано на рисунке.
Решению исходного неравенства соответствуют дуги единичной окружности в тех областях, которые отмечены на рис. 1 знаком « - ». Итак, окончательное решение:

Слайд 13
Пример № 2. Решить неравенство cos3x + cos 0
Решение
Приведем левую часть неравенства к виду 2cos2хсоsх0 . Kорни выражения, стоящего в левой части исходного неравенства, такие же, как и в примере №1. Расположение контрольной точки А аналогичное, как на рис. 1 Решению исходного неравенства соответствуют дуги единичной окружности в тех областях, которые отмечены на рис. 1 знаком « + ». При записи окончательного ответа следует иметь в виду, что в одной из областей (она показана пунктирной стрелкой) нарушается переход от меньших значений х к большим. В таком случае следует к меньшему значению ( 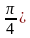 прибавить 2
прибавить 2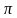 или от большего значения (
или от большего значения ( ) отнять 2
) отнять 2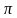 .
.
Итак, окончательное решение можно записать в виде совокупности промежутков:
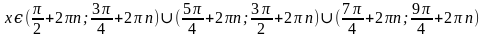
Примечание. Рассмотренные примеры имеют одну особенность. Серии х1 и х2 дают на единичной окружности несовпадающие точки. Если же некоторые точки разных серий совпадают, то будем называть их кратными. Точки, которые повторяются в четном числе серий, будем называть точками четной кратности, а те, что повторяются в нечетном числе серий,— точками нечетной кратности. Волнообразная линия, идущая от точки А, после встречи с точкой нечетной кратности обязана перейти в иную область, т. е. если она находилась вне единичной окружности, то теперь будет внутри нее, и наоборот. Но точка четной кратности не дает нашей линии возможности перейти в иную область. Поясним сказанное.
Слайд 14
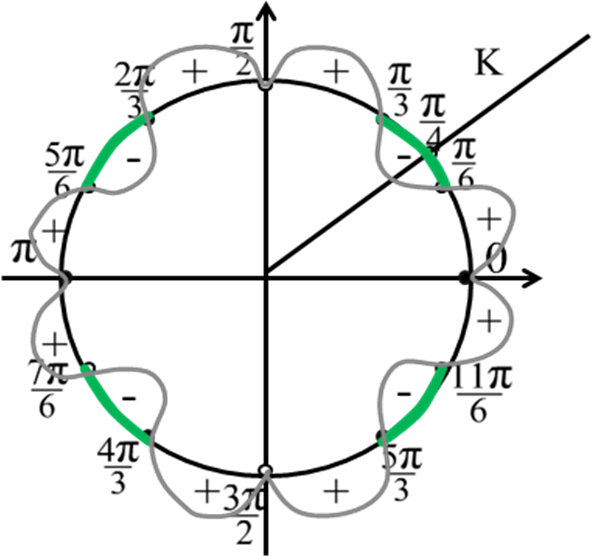
Пример № 3. Решить неравенство 
Решение:
Найдём нули выражения sin3x  sin2x
sin2x  sinx
sinx  cosx. Получaeм:
cosx. Получaeм:
sin3x = 0 , x1 =  ; sin2x = 0, x2 =
; sin2x = 0, x2 =  ;
;
sin x = 0, x3 =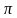 n; cos x = 0, x4 =
n; cos x = 0, x4 =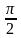 +
+ 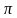 n.
n.
На единичной окружности значения серии х1 представлены точками 0, ,
,  ,
,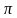 ,
, 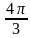 ,
, 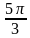 . Серия х2 дает точки 0,
. Серия х2 дает точки 0, 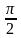 ,
,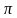 ,
, . Из серии х3 получаем две точки 0,
. Из серии х3 получаем две точки 0,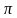 . Наконец, серию х4 будут представлять точки
. Наконец, серию х4 будут представлять точки 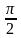 и
и  . Нанесем все эти точки на единичную окружность, указав в скобках рядом с каждой из них ее кратность.
. Нанесем все эти точки на единичную окружность, указав в скобках рядом с каждой из них ее кратность.
Пусть теперь число  будет равным
будет равным  . Делаем прикидку по знаку:
. Делаем прикидку по знаку:
sin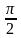 sin
sin sin
sin cos
cos =
= 0
0
Значит, точку A следует выбрать на луче, образующем угол  с лучом Ох, вне единичной окружности. (Заметим, что вспомогательный луч ОA совсем не обязательно изображать на рисунке. Точка A выбирается приблизительно.)
с лучом Ох, вне единичной окружности. (Заметим, что вспомогательный луч ОA совсем не обязательно изображать на рисунке. Точка A выбирается приблизительно.)
Теперь от точки A ведем волнообразную непрерывную линию последовательно ко всем отмеченным точкам. Причем в точках 0,  ,
,  ,
,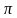 ,
, 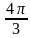 ,
, 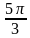 наша линия переходит из одной области в другую: если она находилась вне единичной окружности, то переходит внутрь нее. Подойдя к точке
наша линия переходит из одной области в другую: если она находилась вне единичной окружности, то переходит внутрь нее. Подойдя к точке 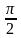 , линия возвращается во внутреннюю область, так как кратность этой точки четная. Аналогично в точке
, линия возвращается во внутреннюю область, так как кратность этой точки четная. Аналогично в точке  (с четной кратностью) линию приходится повернуть во внешнюю область. Итак, мы начертили некую экстравагантную картинку, изображенную на рисунке. Она помогает нам выделить на единичной окружности искомые области. Они обозначены знаком « + ».
(с четной кратностью) линию приходится повернуть во внешнюю область. Итак, мы начертили некую экстравагантную картинку, изображенную на рисунке. Она помогает нам выделить на единичной окружности искомые области. Они обозначены знаком « + ».
Окончательный ответ:
Примечание. Заметим, что если волнообразную линию после обхода ею всех отмеченных на единичной окружности точек не удается вернуть в точку A, не пересекая окружность в «незаконном» месте, то это означает, что в решении допущена ошибка, а именно пропущено нечетное количество корней.
Слайд 15
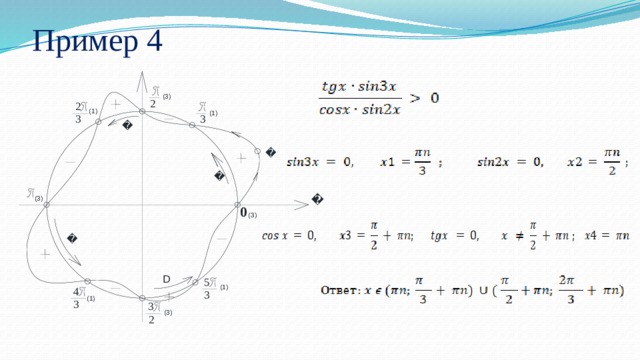
Пример 4. Решить неравенство
Решение:
Найдём нули числителя и знаменателя:
Мы видим, что корни выражения, стоящего в левой части исходного неравенства, такие же, как и в примере 3. Но в связи с ограничениями на значения независимой переменной в серии х4 кратность некоторых точек, соответствующих х2, изменилась.
Подбор значения  и прикидка по знаку происходят так же, как и в примере 3. Но картинка (см. рисунок) изменяется из-за иной кратности точек
и прикидка по знаку происходят так же, как и в примере 3. Но картинка (см. рисунок) изменяется из-за иной кратности точек 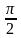 и
и  .
.
При записи ответа заметим, что интервалы M и С, В и D центрально симметричны. Это и отражено во вспомогательной картинке на рис. 3. Поэтому их можно объединить одной записью.
Слайд 16
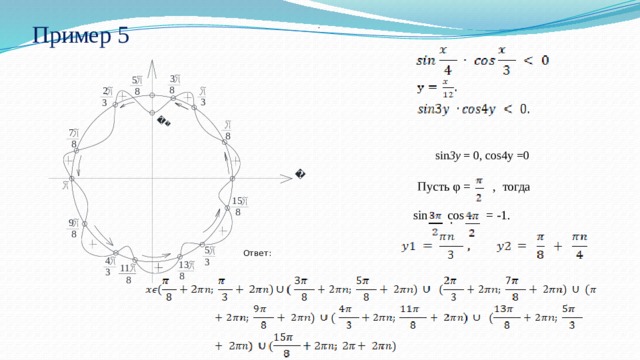
Пример№5. Решить неравенство
Решение. Найдем наименьшее общее кратное знаменателей дробей — число 12 — и сделаем в исходном неравенстве замену  Тогда оно примет вид Решение последнего неравенства проводится так же, как и предыдущих. Из уравнений
Тогда оно примет вид Решение последнего неравенства проводится так же, как и предыдущих. Из уравнений
sin3y = 0, cos4y =0 получаем
На тригонометрической окружности отметим все точки, которые представляют серии значений у1 и у2. Положим  =
= 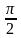 . Тогда sin
. Тогда sin cos
cos = — 1. Значит, точку A нужно взять на луче ОA внутри окружности. Линия, начинающаяся в точке A, перейдет из внутренней части окружности во внешнюю в каждой из отмеченных точек (см. рисунок). Все области, имеющие на рисунке знак « - », дают искомые значения у, из которых умножением на 12 получаем нужные интервалы для значений х.
= — 1. Значит, точку A нужно взять на луче ОA внутри окружности. Линия, начинающаяся в точке A, перейдет из внутренней части окружности во внешнюю в каждой из отмеченных точек (см. рисунок). Все области, имеющие на рисунке знак « - », дают искомые значения у, из которых умножением на 12 получаем нужные интервалы для значений х.
Ответ:
Слайд 17
Одноклассникам было предложено решить 5 неравенств методом интервалов
1 этап – решение предложенного
набора задач ( 5 мин)
2 этап –
объяснение
способов
решений ( 5 мин)
3 этап – решение нового
набора задач ( 20 мин)
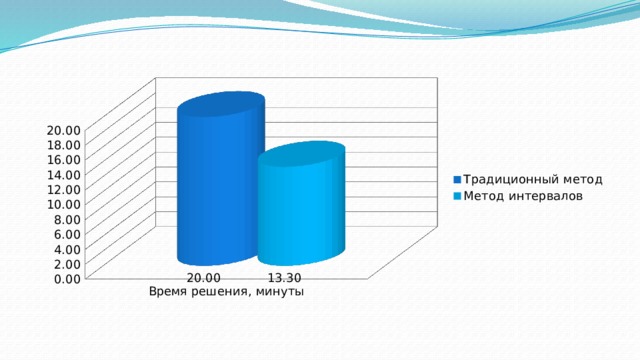
В ходе работы установлено: время решения сократилось на треть, ошибок стало меньше на 10%.
Слайд 18
Слайд 19
Преимущество метода интервалов по сравнению с другими, использующимися при решении такого же рода задач, следующие:
- простота и быстрота достижения цели;
- наглядность (и возможность контроля или перепроверки);
- экономность в вычислительных средствах и времени;
- широта охвата всей ситуации;
- формирование и развитие навыков обобщенного мышления и анализа, а также связанные с этим умения делать логические выводы.
Слайд 20
Заключение
Рассмотрев серию заданий, которые приводят к решению тригонометрических неравенств методом интервалов, можно сделать вывод, что метод интервалов является наиболее ценным и даже универсальным для решения различных неравенств как простого, так и сложного вида.
Слайд 21
Слайд 22








 Второе из уравнений
Второе из уравнений 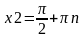 .
.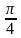 ,
,  ,
, 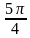 ,
, (при остальных значениях
(при остальных значениях 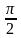 и
и  , которые получены при
, которые получены при  =0. Тогда
=0. Тогда 

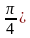 прибавить 2
прибавить 2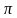 или от большего значения (
или от большего значения ( ) отнять 2
) отнять 2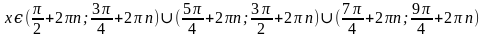




 ,
,  ,
,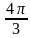 ,
, 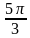 . Серия х2 дает точки 0,
. Серия х2 дает точки 0,  . Делаем прикидку по знаку:
. Делаем прикидку по знаку: 0
0








 0 - тригонометрическое неравенство, а T - наименьший период (часть оси Ох), на котором помещаются все серии значений x. Построим на этой части оси схему знакопостоянства функции f(х) по методу интервалов. Она будет походить на волнообразную линию на отрезке [0; T]. Возьмем окружность длины T и «намотаем» на нее отрезок [0; T]. Тогда волнообразная линия обовьет окружность так, что ее «отрицательные» части окажутся внутри окружности, а «положительные» - вне ее. Картина будет повторяться, если продолжать «наматывание» на окружность отрезков длины [Т, 2T], [2T, 3T] и т. д. вдоль положительной части оси Ох, а затем и вдоль ее отрицательной части." width="640"
0 - тригонометрическое неравенство, а T - наименьший период (часть оси Ох), на котором помещаются все серии значений x. Построим на этой части оси схему знакопостоянства функции f(х) по методу интервалов. Она будет походить на волнообразную линию на отрезке [0; T]. Возьмем окружность длины T и «намотаем» на нее отрезок [0; T]. Тогда волнообразная линия обовьет окружность так, что ее «отрицательные» части окажутся внутри окружности, а «положительные» - вне ее. Картина будет повторяться, если продолжать «наматывание» на окружность отрезков длины [Т, 2T], [2T, 3T] и т. д. вдоль положительной части оси Ох, а затем и вдоль ее отрицательной части." width="640"
 0 Ответ:" width="640"
0 Ответ:" width="640"
 0 ; 2cos 2x cos x = 0 ; cos 2x = 0, cos x = 0 Для I серии x : n= 0, 1, 2, 3 : Выберем теперь контрольную точку, взяв φ=0. Тогда сos0 + cos0 = 2 0 Для II серии x : n = 0, 1: Ответ:" width="640"
0 ; 2cos 2x cos x = 0 ; cos 2x = 0, cos x = 0 Для I серии x : n= 0, 1, 2, 3 : Выберем теперь контрольную точку, взяв φ=0. Тогда сos0 + cos0 = 2 0 Для II серии x : n = 0, 1: Ответ:" width="640"
 0 . Решение: sin3 x sin2 x sin x cosx =0 sin3 x = 0 , x 1 = sin2x = 0, x 2 = ; sin x = 0, x 3 = n , cos x = 0; x 4 = + n. х 1 : 0 , , , , , . х 2 : 0, , , . х 3 : 0, . х 4 : и . Ответ: ) +" width="640"
0 . Решение: sin3 x sin2 x sin x cosx =0 sin3 x = 0 , x 1 = sin2x = 0, x 2 = ; sin x = 0, x 3 = n , cos x = 0; x 4 = + n. х 1 : 0 , , , , , . х 2 : 0, , , . х 3 : 0, . х 4 : и . Ответ: ) +" width="640"