ПРОЕКТ на тему: «
Решение логарифмических уравнений и неравенств»
Яралиева Б.С. преподаватель математики «Дербентского профессионально- -педагогического колледжа»
-2016г.-
Содержание
Введение……………………………………………………………………3 Глава 1. Теоретические основы. 1.1. Основные понятия…………………………………………………….4
1.2. Методы решения логарифмических уравнений и неравенств…......7
Глава 2. Применение методов на практике.
2.1.Решение логарифмических уравнений…………………………..…..10
2.2.Решение логарифмических неравенств……………………………...13
Выводы……………………………………………………………….…….16
Заключение…………………………………………………………….…..17
Список литературы…………………………………………………….….18
Введение
Тема проекта: «Решение логарифмических уравнений и неравенств»
Актуальность: - учащиеся не обладают достаточными знаниями о методах решения логарифмических уравнений и неравенств;
- в материалах ЕГЭ встречаются задания, содержащие логарифмические уравнения и неравенства.
Цель: сформировать у учащихся умение решать различного типа логарифмические уравнения и неравенства для успешной сдачи ЕГЭ.
Задачи: собрать и изучить теоретический материал по способам решения логарифмических уравнений и неравенств; описать различные способы их решений и показать учащимся применение рассмотренных методов на примерах.
Объект исследования: процесс обучения учащихся решению логарифмических уравнений и неравенств на уроках математики.
Предмет исследования: методы решения логарифмических уравнений и неравенств.
Гипотеза исследования основана на предположении о том, что знание различных методов решения логарифмических уравнений и неравенств может повысить эффективность изучения данной темы и качество подготовки обучающихся к сдаче ЕГЭ.
Методы исследования: изучение специализированной литературы, анализ, сравнение, применение теоретических знаний при решении практических задач.
Выборка исследования: различные методы решений логарифмических уравнений и неравенств.
Глава 1. Теоретические основы. 1.1. Основные понятия.
- Логарифмы и их свойства
Рассмотрим уравнение 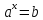 , при
, при 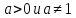 . При
. При 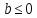 это уравнение не имеет решений и при
это уравнение не имеет решений и при 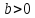 имеет единственное решение. Данное решение называют логарифмом
имеет единственное решение. Данное решение называют логарифмом 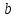 по основанию
по основанию 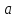 и обозначают
и обозначают 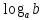 .
.
Логарифмом числа 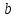 по основанию
по основанию 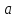 называется показатель степени, в которую необходимо возвести число
называется показатель степени, в которую необходимо возвести число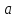 , чтобы получилось число
, чтобы получилось число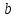 :
:
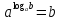 .
.
Это равенство называют основным логарифмическим тождеством
Свойства логарифмов
При 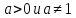 .
. 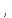
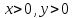 и действительном
и действительном 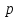 имеют место равенства:
имеют место равенства:
1. 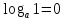 ;
;
2.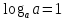 ;
;
3. 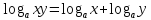 ;
;
4.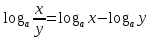 ;
;
5.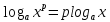 .
.
Формула перехода к новому основанию:
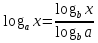
Имеет место тождество
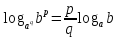 .
.
Из него следуют следующие равенства:
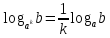 ,
, 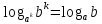 .
.
Так же имеет место равенство

Логарифм, основанием которого является число 10, называют десятичным логарифмом и обозначают  . Логарифм, основанием которого является число e, называют натуральным логарифмом и обозначают
. Логарифм, основанием которого является число e, называют натуральным логарифмом и обозначают  .
.
2.Логарифмическая функция
Определение
Функцию вида  , где
, где 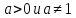 называют логарифмической функцией с основанием
называют логарифмической функцией с основанием 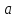 .
.
Основные свойства логарифмической функции:
1. Область определения логарифмической функции есть множество положительных вещественных чисел - R+.
2. Область значения логарифмической функции есть множество вещественных чисел.
3. Если основание логарифмической функции  , то функция возрастает на всей области определения. Если же для основания логарифмической функции имеет место неравенство
, то функция возрастает на всей области определения. Если же для основания логарифмической функции имеет место неравенство  , то логарифмическая функция убывает на всей области определения.
, то логарифмическая функция убывает на всей области определения.
4. График логарифмической функции всегда проходит через точку (1;0).
5. Возрастающая логарифмическая функция положительна при  и отрицательна при
и отрицательна при  .
.
6. Убывающая логарифмическая функция отрицательна при  и положительна при
и положительна при  .
.
График возрастающей логарифмической функции - ( ):
):
График убывающей логарифмической функции - ( ):
):
7. Функция не является четной или нечетной. Логарифмическая функция – функция общего вида.
8. У функции нет точек максимума и минимума.
Графики показательной и логарифмической функций с одинаковыми основаниями симметричны относительно прямой  .
.
Логарифмические уравнения и неравенства.
Определение.
Логарифмическим уравнением называется уравнение, содержащее неизвестное под знаком логарифма или (и) в его основании.
Простейшим логарифмическим уравнением является уравнение вида
 . Тогда
. Тогда  .
.
Определение.
Логарифмическим неравенством называется неравенство, содержащее неизвестное под знаком логарифма или (и) в его основании.
1.2. Методы решения логарифмических уравнений и неравенств.
При решении логарифмических уравнений используют различные методы. Выбор метода зависит от вида уравнения. Перечислим некоторые из них:
Использование определения логарифма
Потенцирование (переход от логарифма данного выражения к самому этому выражению).
Приведение к одному основанию.
Введение новой переменной.
Логарифмирование обеих частей уравнения.
Функционально-графический метод.
Для решения логарифмических неравенств часто используются следующие утверждения относительно равносильности неравенств и учитываются свойства монотонности логарифмической функции.
1. Если a 1, то неравенство равносильно системе неравенств
2. Если 0 a равносильно системе неравенств
| 
| f(x) , |
| f(x) 0. |
3. Неравенство равносильно совокупности систем неравенств
4. Знак  совпадает со знаком
совпадает со знаком  в ОДЗ.
в ОДЗ.
5. Знак разности совпадает со знаком произведения в ОДЗ.
В работе использовала следующие источники:
- И.В. Яковлев Логарифмические уравнения и неравенства. Материалы по математике. MathUs.ru
- Башмаков М.И. Математика 2012 г.
- В.Г. Рисберг, И.Ю.Чернилова Решение показательныч и логарифмических уравнений, неравенств и систем уравнений повышенного и высокого уровня сложности. Учебное пособие. 2015 г.
- Шувалова Э.З., Агафонов Б.Г., Богатырев Г.И. Повторим математику.
5.Эфендиев Э.И.- Практикум по элементарной математике-2015 г.
6. Колмогоров А.Н.- Алгебра и начала анализа.-2013 г. (учебник 10-11кл)
7. https://infourok.ru
В источниках [1], [3] очень хорошо раскрыт метод рационализации, суть которого высказана у нас в утверждениях 4 и 5.
В источниках [4], [5], [6] приведены задания, во всей полноте характеризующие тот или иной метод решения логарифмических уравнений и неравенств.
Из источника [3] взяты задания повышенного уровня.
Проанализировав материал школьных учебников по алгебре и началам математического анализа для 10 – 11 классов, могу сделать вывод о недостаточном освещении изучаемого вопроса в учебно-методической литературе. Это затрудняет работу учителя при изучении данной темы и подготовке к сдаче ЕГЭ.
В источниках [6], [2] при рассмотрении темы «Решение логарифмических уравнении и неравенств» приведены лишь методы решения уравнений с использованием определения логарифма, потенцирования и перехода к одному основанию. А ведь есть и другие методы. Знание различных методов облегчило бы учащимся выполнение заданий с логарифмическими уравнениями. Надо учитывать, что задания в материалах ЕГЭ сложнее заданий в школьных учебниках (задания С). Так же обстоит дело с решением логарифмических неравенств. Метод рационализации намного упростил бы их решение. Он позволяет в определённых случаях упростить неравенство и свести его к рациональному неравенству (которое решается методом интервалов).
Выводы: изучаемая нами тема в различных источниках преподносится в разной последовательности и форме.
Глава 2. Применение методов на практике.
2.1.Решение логарифмических уравнений.
Рассмотрим применение приведенных методов при решении логарифмических уравнений.
Используя определение логарифма
Решить уравнения: а) 
б) 
в) 
Решения: а) 


Проверка:  ,
,  является решением.
является решением.
Ответ: 15.
б) 




Сделав проверку, убеждаемся в том, что  наше решение.
наше решение.
Ответ:2.
в) 




После проверки остается корень  .
.
Ответ:0.
Потенцирование (переход от логарифма данного выражения к самому этому выражению).
Решить уравнения: а)
б)
Решения: а) log3 (x+1)+log3 (x+3)=log33
ОДЗ: 
 x
x
Используя свойство логарифмов, получаем:
log3 (x+1)(x+3)=log33
(x+1)(x+3)=3
x2 +4x+3=3
x2 +4x=0
x1 =0 x2 =-4
Учитывая ОДЗ, получаем решение x=0.
Ответ:0.
б)
ОДЗ: 
 x
x


x1=-3 , x2=2
С учетом ОДЗ получаем x=2.
Ответ:2.
В общем виде уравнение logaf(x)=logag(x) решается переходом к равносильной системе
.
Приведение к одному основанию.
Решить уравнение log25x+log5x=log0,2
ОДЗ: x0. Перейдем к основанию 5.
log52x+log5x=log5-1
 log5x+log5x=-log5
log5x+log5x=-log5
 log5x=-log523/2
log5x=-log523/2
log5x3/2 =log52-3/2
x=
Ответ: x= .
.
Введение новой переменной.
Решить уравнение log2 5x-log5x=2.
ОДЗ: x0. Введем новую переменную y=log5x , получим квадратное уравнение y2 -y -2=0.Оно имеет корни y1=-1, y2=2. Вернувшись к замене, получаем простейшие логарифмические уравнения:
log5x 1, x=5-1=
1, x=5-1=
log5x=2, x=52=25.
Оба корня входят в ОДЗ.
Ответ: x= , x=25.
, x=25.
Логарифмирование обеих частей уравнения.
Решить уравнение  .
.
ОДЗ: x
После подстановки полученного выражения наше уравнение примет вид: 

Прологарифмировав обе части уравнения по основанию 2, получим: 



Входит в ОДЗ.
Ответ:2.
Функционально-графический метод.
Если одна из функций у = f(x) возрастает, а другая y = g(x) убывает на промежутке Х, то уравнение f(x)= g(x) имеет не более одного корня на промежутке Х.
Решить уравнение log5(x+2)=4-x.
ОДЗ: x-2.
Очевидно, что x=3 является решением уравнения. Так как левая часть нашего уравнения есть строго возрастающая функция, а правая – строго убывающая, то других решений уравнение не имеет.
2.2.Решение логарифмических неравенств.
Рассмотрим применение приведенных утверждений при решении логарифмических неравенств.
Решить неравенства:
а)
Согласно утверждению 1 оно равносильно системе
Ответ: 
б)
Согласно утверждению 2 оно равносильно системе
Ответ: 
в) Решить неравенство .
Представим  . Тогда, используя утверждение 3, можем записать:
. Тогда, используя утверждение 3, можем записать:
Решая первую систему совокупности, получаем:
.
Решая вторую систему совокупности, получаем:
.
И решение нашего неравенства примет вид: .
Решим это неравенство используя утверждение 5.
Оно равносильно системе:
Ответ:
Мы видим, что это решение намного проще.
Решим этим же методом следующее неравенство
.
ОДЗ:
Наше неравенство с учетом утв. 5 примет вид
(
 ,
,
решением которого является множество .
С учетом ОДЗ получаем решение нашего неравенства:  .
.
Ответ:  .
.
Рассмотрим еще одно неравенство.

Решение
ОДЗ: 
т.к.  .
.
Это неравенство равносильно следующей системе:
Отсюда получаем решение: . Ответ:.
Выводы
В результате анализа использованной литературы и проведенного эмпирического исследования пришла к следующим выводам:
- о недостаточном освещении изучаемого вопроса в учебно-методической литературе;
- о необходимости внедрять в учебный процесс изучение методов, облегчающих выполнение заданий по данной теме;
- о необходимости научить учащихся правильному применению
изученных методов на практике.
Полностью согласна со следующим высказыванием Г.Цейтена: «Правильному применению методов можно научиться только применяя их на разнообразных примерах.»
Надеюсь, что результаты моей работы помогут учащимся в решении заданий по данной теме.
Заключение
В школьном курсе математике изучаются логарифмические уравнения и неравенства и способы их решения очень сжато. Потребности учебного процесса требуют от учеников больших знаний и умений.
В материалах ЕГЭ и на олимпиадах часто встречаются задания с логарифмическими уравнениями и неравенствами.
В своей работе мы рассмотрели различные методы решений логарифмических уравнений и неравенств: использования определения логарифма, потенцирования, перехода к одному основанию, логарифмирования, функционально - графический, рационализации, использования свойств логарифмической функции.
Результаты данной работа могут быть использованы при подготовке к выпускным и вступительным экзаменам, и на факультативных занятиях для расширения математического кругозора учащихся.
В дальнейшем планируя исследовать уравнения в целых числах, способы их решений.
Список литературы
Колмогоров А.Н.- Алгебра и начала анализа.-2013 г. (учебник 10-11кл)
- Рисберг В.Г., Чернилова И.Ю. Решение показательныч и логарифмических уравнений, неравенств и систем уравнений повышенного и высокого уровня сложности. Учебное пособие. 2015 г.
- Шувалова Э.З., Агафонов Б.Г., Богатырев Г.И. Повторим математику.
Эфендиев Э.И. Практикум по элементарной математике-2015 г.
- Яковлев И.В. Логарифмические уравнения и неравенства. Материалы по математике. MathUs.ru
https://infourok.ru






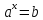 , при
, при 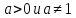 . При
. При 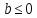 это уравнение не имеет решений и при
это уравнение не имеет решений и при 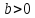 имеет единственное решение. Данное решение называют логарифмом
имеет единственное решение. Данное решение называют логарифмом 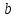 по основанию
по основанию 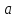 и обозначают
и обозначают 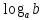 .
.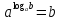 .
.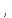
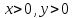 и действительном
и действительном 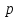 имеют место равенства:
имеют место равенства: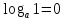 ;
; 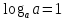 ;
;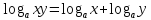 ;
;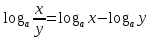 ;
;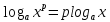 .
.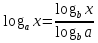
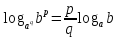 .
.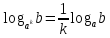 ,
, 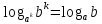 .
.


















