РЕФЕРАТ
на тему: «Теорема Виета и симметрические многочлены»
2021
Содержание
Введение…………………………………………………………….…………..…3
Биография Франсуа Виета………………………………….…………….4
Применение теоремы Виета……………………………………………….6
Симметрические многочлены……………………….………..………….12
Заключение……………………………………………………………………....18
Список использованных источников………………………………………….19
Введение
Проблемы с симметрическими многочленами часто встречаются на олимпиадах и различных тестах. Решить многие задачи элементарной алгебры намного проще, если использовать симметрию условия задачи. В этой работе показано, как использовать симметрию при решении систем уравнений, иррациональных уравнений, неравенств и т. д. Все эти задачи решаются единым методом, основанным на теории симметричных многочленов.
Не все знают, какие замены нужно сделать, чтобы свести эти задачи к более простым. Наша работа посвящена изучению этого вопроса, мы не только указываем на эти подстановки, но и доказываем теорему о том, что они всегда приводят к результату, этот факт школьники принимают как должное. Доказательство проводится элементарными методами.
1.Биография Франсуа Виета
Франсуа Виет - замечательный французский математик, заложивший основы алгебры как науки о преобразовании выражений, решении уравнений в общем виде, создатель алфавитных вычислений.
Виет был первым, кто использовал буквы для обозначения не только неизвестных, но и заранее определенных сумм. Так ему удалось внедрить в науку великую идею возможности выполнения алгебраических преобразований символов, то есть понятие математической формулы. Тем самым он внес решающий вклад в появление алфавитной алгебры, которая завершила развитие математики эпохи Возрождения и проложила путь к появлению результатов Ферма, Декарта и Ньютона.
Франсуа Виет родился в небольшом городке Фантине-ле-Конт на юге Франции в 1540 году. Отец Вита был прокурором. Традиционно сын выбрал профессию отца и стал юристом, окончив университет Пуату.
В 1671 году Виет поступил на государственную службу, стал советником парламента, а затем советником короля Генриха III. из Франции.
Находясь на государственной службе, Виет оставался ученым. Он прославился тем, что смог расшифровать код перехваченной переписки между королем Испании и его представителями в Нидерландах, благодаря чему король Франции полностью знал действия своих противников. Код был сложным и содержал до 600 различных символов, которые регулярно менялись. Испанцы не поверили расшифровке и обвинили французского короля в связях со злыми духами.
К этому времени относятся свидетельства современников Виета о его огромной трудоспособности. Поскольку ученый чем-то увлекался, он мог работать без сна три дня.
В 1584 году по настоянию догадок Виета был отстранен от должности и изгнан из Парижа. На это время приходится пик его творчества. Ученый обрел неожиданное спокойствие и расслабление и поставил перед собой цель создать всеобъемлющую математику, которая позволит ему решить любую задачу. Он развил убеждение, что должна существовать «общая, пока неизвестная наука, включающая как гениальные изобретения новейших алгебраистов, так и глубокие геометрические исследования древности».
Виет изложил программу своих исследований и перечислил трактаты, объединенные общей идеей и написанные на математическом языке новой алфавитной алгебры, в знаменитом «Введение в аналитическое искусство», опубликованном в 1591 году. Однако основная идея ученого оказалась на удивление успешной: началось преобразование алгебры в мощное математическое вычисление. Название «алгебра» Виет заменил в своих трудах слова «аналитическое искусство».
Виет назвал основу своего подхода видовой логистикой. Следуя примеру древних, он четко различал числа, размеры и отношения и собирал их в определенную систему «типов». В эту систему входили переменные, их их корни, квадраты, кубы, квадрато - квадраты и т. д., а также ряд скаляров, соответствующих реальным размерам - длине, площади или объему. Для этих видов Виет дал специальные символы и обозначил их заглавными буквами латинского алфавита. Гласные использовались для неизвестных величин, согласные - для переменных.
Виет показал, что, работая с символами, можно получить результат, применимый ко всем соответствующим величинам, то есть решить задачу в общем виде. Это положило начало радикальному повороту в развитии алгебры: стало возможным буквальное исчисление.
Чтобы продемонстрировать эффективность своего метода, ученый привел в своих работах ряд формул, с помощью которых можно было решить конкретные проблемы. Из знаков действия он использовал «+» и «-», радикальный знак и горизонтальную линию для разделения. Товар был обозначен словом «in». Виет был первым, кто использовал скобки, но они были не в скобках, а как линии над многочленом. Но он не использовал многие из представленных до него знаков. Итак, квадрат, куб и т. д. обозначаются словами или первыми буквами слов.
Знаменитая теорема, устанавливающая связь между коэффициентами многочлена и его корнями, была опубликована в 1591 году. Теперь это называется Виета, а сам автор формулировал ее так: «Если В + D, умноженное на А, минус А в квадрате равно ВD, то А равно В и равно D».
Теорема Виета стала самым известным утверждением школьной алгебры. Теорема Виета достойна восхищения, особенно потому, что ее можно обобщить на многочлены любой степени.
Глубокие знания алгебры давали Виету большие преимущества. Кроме того, его интерес к алгебре первоначально был вызван приложениями в тригонометрии и астрономии. Каждое новое применение алгебры не только давало толчок новым исследованиям в тригонометрии, но и полученные тригонометрические результаты были также источником важных достижений в алгебре. Виет особенно ответственен за вывод выражений для синусов (или аккордов) и косинусов нескольких дуг.
В последние годы жизни Виет ушел с государственной службы, но продолжал интересоваться наукой. Например, известно, что он вызвал споры по поводу введения нового григорианского календаря в Европе. И даже хотел создать свой собственный календарь.
2. Применение теоремы Виета
Теорема Виета в массовом школьном сознании ассоциируется с нахождением корней квадратного уравнения. Для одних это какое-то магическое заклинание, позволяющее решать задачу «не через дискриминант», для других действенный способ сэкономить время на решении.
Мы предполагаем, что большинство читающих умеют применять эту теорему для поиска корней квадратного уравнения, поэтому поговорим о некоторых тонкостях её использования.
Как на практике подбирать корни
Часть учеников, даже выписав соотношение между корнями и коэффициентами квадратного уравнения, всё равно испытывают трудности с подбором корней.
Дело в том, что многие школьники считают подбор неким бессистемным действием сродни хаотичной стрельбе с закрытыми глазами. Однако, любой подбор должен быть осознанным перебором, то есть в основе иметь какую-то логику.
Проблема состоит ещё и в том, что те, кто умеют быстро подбирать значения, сами порой не осознают, что делают это не интуитивно, а по некой системе. В итоге они не задумываются над своими действиями и не могут объяснить другим, как рассуждают, считая, что «всё очевидно». Тем самым для остальных практическое применение теоремы Виета становится магией для посвященных.
Хотя достаточно одной идеи, чтобы значительно ускорить перебор вариантов.
Итак, давайте рассмотрим квадратное уравнение x²-8x+15=0, которое даёт нам вот такие условия для корней:
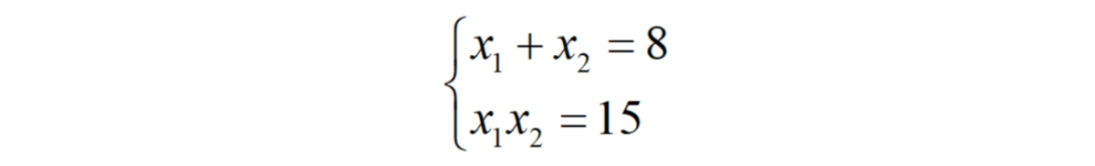
Обычно их выписывают именно в таком порядке: первым соотношением идёт сумма, а затем произведение. Это и играет злую шутку с учениками. Они начинают ориентироваться на первое равенство и перебирать варианты целых слагаемых, которые потом подставляют во второе соотношение. В итоге тратится много сил на лишние (хотя в данном случае и довольно быстрые) вычисления.
Cекрет же эффективного перебора прост: надо начинать со второго соотношения, то есть отталкиваться от произведения.
В предложенном примере возможны два варианта: 15 = 3 ⋅ 5 = 1 ⋅ 15. Конечно, здесь мы сразу учли поправку на знаки множителей. Так как произведение положительно, то знаки множителей совпадают, а так как сумма тоже положительна, то и сами числа тоже положительные. В итоге благодаря разложению на множители и последующей проверке суммы легко находим, что это числа 3 и 5.
Иногда, конечно, бывают неприятные числа, которые допускают больше вариантов разложения на множители. Например, 24, 36 или 48. Но такие случаи довольно редки и обычно грамотный перебор допускает не более 3-4 вариантов.
Отметим также, что хотя теорема Виета работает для любых действительных корней, её в таком виде лучше использовать, когда первый коэффициент a равен единице. В этом случае корни будут целыми и подбор будет эффективным. Иначе следует сразу честно считать через дискриминант.
И конечно, надо учитывать, что в некоторых ситуациях подбор корней бессмысленен. Например, в случае иррациональных корней или если действительных корней вообще нет. В таком случае мы советуем ученикам применять правило «10 секунд»: если за это время не удалось подобрать корни — считайте честно через дискриминант.
Полезные соотношения между коэффициентами (а+b+c=0 и а-b+c=0)
Теорема Виета позволяет не только подбирать корни, но даёт два интересных следствия, про которые мы писали в прошлом году. Они настолько важные, что повторим наши рассуждения и здесь.
Допустим, что вы столкнулись с квадратным уравнением, в котором сумма коэффициентов равна 0. То есть для уравнения аx²+bx+c=0 выполнено условие а+b+c=0.
Для удобства давайте сразу будем работать с конкретным уравнением. Например, для определённости возьмём такое уравнение: 4x²-5x+1=0. Очевидно, что 4-5+1=0. И это означает, что единица автоматически является решением. Действительно, подставим её в наше уравнение: 4⋅1²-5⋅1+1=4-5+1=0 и убедимся, что это так.
Далее используем теорему Виета: произведение корней равно с/а. А так как один и них равен 1, то легко получаем, что второй равен с/а. А в нашем конкретном примере второй корень равен 1/4.
Рассуждения для случая а-b+c=0 аналогичны. Там один из корней равен -1.
В итоге мы получаем вот такие интересные ситуации, при которых корни находятся мгновенно:
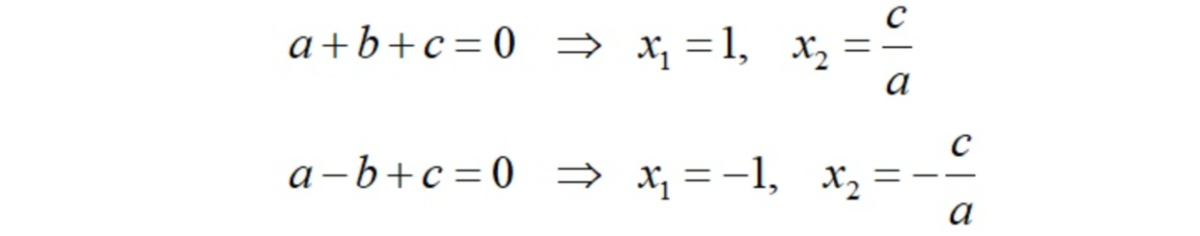
Уравнения с такими условиями на практике встречаются довольно часто. Составители задач ленятся придумывать новые квадратные уравнения и пользуются указанными соотношениями.
Удивительно, что этот приём знают далеко не все ученики физмат классов, хотя он позволяет существенно сократить время решения простых задач.
Быстрая проверка корней
Ещё одно применение теоремы Виета, про которое забывают многие ученики, — это проверка найденных корней. Она позволяет мгновенно проверить рациональные корни вашего квадратного уравнения, если вы их считали через дискриминант.
Например, есть уравнение 48x²-46x+5=0. После некоторых вычислений получаем корни 1/8 и 5/6. Можно сразу выписать их в ответ, а можно потратить 2-3 секунды и убедиться, что 1/8⋅5/6=5/48, то есть выполнено одно из соотношений в теореме Виета и x₁x₂=c/a.
Конечно, одна эта проверка не является абсолютной гарантией правильности найденных корней. Но как минимум в 95% случаев она вылавливает ошибки. Особенно хорошо она вылавливает случаи, когда ученики забывают что-то разделить или умножить (например, забывают указать двойку в знаменателе для корней).
Если же вы хотите стопроцентной уверенности в найденных корнях, можете проверить и другое условие — для суммы корней.
Формулы Виета для кубического уравнения
Теорема Виета работает не только для квадратного уравнения. Её можно использовать для многочленов любой степени.
Второй по распространённости применения этой теоремы идёт (правда с большим отрывом) многочлен третьей степени.
Пусть у нас есть кубическое уравнение ax³+bx²+cx+d=0, которое имеет три действительных корня. Тогда многочлен слева можно представить в виде:
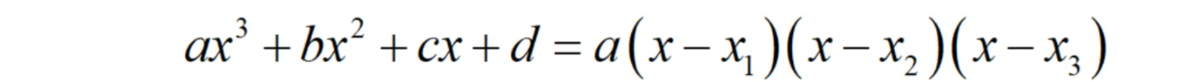
Раскрываем справа скобки и приводим подобные слагаемые. В итоге получаем следующую картину:
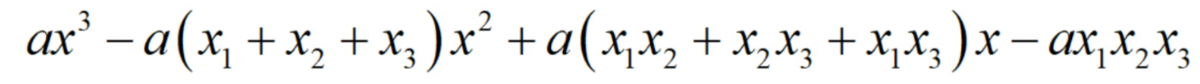
Приравниваем коэффициенты и получаем следующие соотношения:
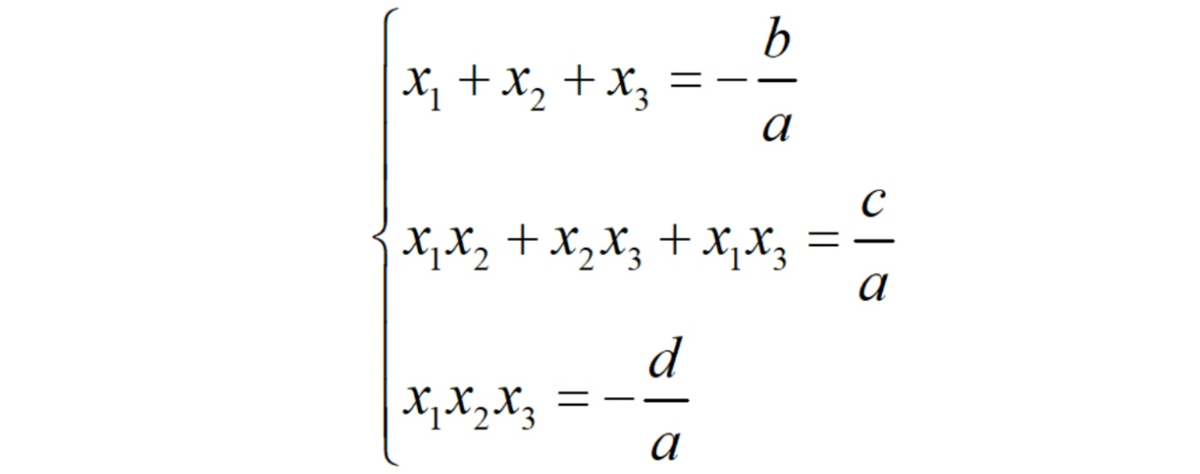
В школьных задачах и стандартных экзаменах формулы Виета для кубического уравнения не применяются, но на вступительных испытаниях более высокого уровня вполне могут пригодиться. Например, они дважды использовались вот в такой физтеховской задаче-монстре.
Неправильное употребление названия теоремы
Нужно понимать, что при поиске корней квадратного уравнения мы всё-таки используем не теорему Виета, а обратную теорему Виета. И правильно говорить, что мы ищем корни «методом подбора с проверкой по теореме, обратной теореме Виета». Вот здесь давний подписчик нашей группы указывает на отличия и призывает преподавателей к правильному произношению. Цель понятна — воспитать у учеников математическую грамотность и умение чётко проговаривать формулировки.
Однако, некоторые внимательные зрители заметили, что в наших видеоразборах задач мы всё равно говорим про «теорему Виета» и не испытываем при этом угрызений совести. Даже в этой статье мы очень вольно с ней обращаемся, не указывая её как прямую или обратную.
Мы считаем, что пусть так в строгом смысле говорить и не правильно, но при решении задач это допустимо. Тут, конечно, важен контекст. Когда мы говорим, что решаем КУ по теореме Виета, мы подразумеваем, что будем использовать некое стандартное соотношение, которое поможет нам с поиском корней. Это уже стало расхожим методом и на практике прямую теорему Виета для квадратного уравнения не используют (проще явно в уме перемножить два двучлена).
Конечно, когда были устные экзамены на какой-нибудь мехмат, то могли придраться к подобной формулировке. Но на письме всё же обычно хватает просто писать в скобках «т.Виета». А если есть опасения, то могут придраться, то можно где-то в стороне найти эти корни, а в решении просто их выписать в явном в виде без указания способа поиска. Может вас вообще просто озарило и вы их нашли, пристально вглядываясь в уравнение.
При том, что подобное вольное применение допустимо для теоремы Виета, это не значит, что мы можем использовать формулировки как хотим.
Например, теорему Пифагора и обратную теорему Пифагора важно чётко различать. Но в отличие от т.Виета, которая в реальных задачах чаще всего используется только в одну сторону, для теоремы Пифагора в реальных задачах применяется и прямая и обратная формулировка.
Вот, например, такое задание из задачника Гордина:

В решении прописана обратная теорема, хотя это и не сказано в явном виде:
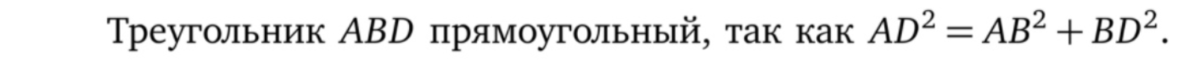
Прямая же теорема Пифагора встречается очень часто, и нет смысла иллюстрировать здесь её применение.
В общем, из-за массового употребления допустимо решать КУ не «методом подбора с проверкой по теореме, обратной теореме Виета», а просто «по теореме Виета». В остальных случаях подобные тонкие моменты надо стараться объяснять чётко.
Однако, если вы учитесь в математическом классе и вас интересует математика как наука, то желательно понимать различия между прямой и обратной теоремой и при необходимости пояснять их применение. В том числе и для теоремы Виета.
3.Симметрические многочлены
Среди многочленов от нескольких неизвестных выделяются те, которые не меняются ни при какой перестановке неизвестных. В такие многочлены все неизвестные входят, следовательно, вполне симметричным образом, и поэтому эти многочлены называются симметрическими многочленами (или симметрическими функциями). Простейшими примерами будут: сумма всех неизвестных x1+ х2 + ... + хn ,сумма квадратов неизвестных х12 + х22 + ... + хn2, произведение неизвестных х1х2...хn и т.д. Сумма, разность и произведение двух симметрических многочленов сами будут симметрическими. Следующие n симметрических многочленов от n неизвестных называются элементарными симметрическими многочленами:
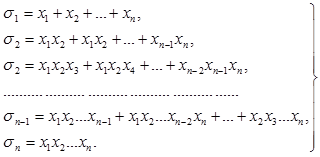 (1)
(1)
Эти многочлены, симметричность которых очевидна, играют в теории симметрических многочленов очень большую роль. Они подсказаны формулами Виета, и поэтому можно сказать, что коэффициенты многочлена от одного неизвестного, имеющего старшим коэффициентом единицу, будут, с точностью до знака, элементарными симметрическими многочленами от его корней.
Симметрическим многочленом будет всякая целая положительная степень любого из элементарных симметрических многочленов, а также произведение таких степеней и всякая сумма указанных произведений. Иными словами, всякий многочлен от элементарных симметрических многочленов 1,2,…, n , рассматриваемый как многочлен от неизвестных х1,х2,...,хn, будет симметрическим. Так, положим n = 3 и возьмем многочлен 12 + 23. Заменяя 1, 2 и 3 их выражениями, мы получим:
12 + 23 = x12x2 + x12x3 + x1x22 + x22x3 + x1x32 + x2x32 + 5x1x2x3;
справа стоит симметрический многочлен от х1, х2, х3.
Обращением этого результата является следующая основная теорема о симметрических многочленах:
Теорема 2.1
Всякий симметрический многочлен от неизвестных х1, х2, ... , хn, является многочленом от элементарных симметрических многочленов 1,2, … , n[2]
Доказательство
Упорядочим данный симметрический многочлен f(x1, x2, … , xn) лексикографически (как в словаре), т.е. таким образом, чтобы слагаемое х1 ... хnn предшествовало слагаемому х1'... хnn в том случае, если первая ненулевая разность i - i положительна. Пусть в его лексикографической записи будет член
а0х1к1х2к2 … хnkn. (2)
Показатели при неизвестных в этом члене должны удовлетворять неравенствам
k1 k2 … kn (3)
Действительно, пусть при некотором i будет ki ki+1. Многочлен f(x1, x2, … , xn), будучи симметрическим, должен содержать член
a0x1k1x2k2 … xiKi+1xi+1ki … xnkn, (4)
получающийся из члена (2) транспозицией неизвестных хi и хi+1.Это приводит нас к противоречию, так как член (4) в смысле лексикографического расположения выше члена (2): показатели при х1, х2, ... , хi-1 в обоих членах совпадают, но показатель при хi в члене (4) больше, чем в члене (2).
Возьмем теперь следующее произведение элементарных симметрических многочленов (ввиду неравенств (3) все показатели будут неотрицательными):
1 = a01k1-k22k2-k3 … n-1Kn-1-KnnKn. (5)
Это будет симметрический многочлен от неизвестных х1, х2, ... , хn , причем его высший член равен члену (2). Действительно, высшие члены многочленов 1,2, 3, … , n равны соответственно x1, x1x2 , x1x2x3 ,…, x1x2 … xn , а так как высший член произведения равен произведению высших членов сомножителей, то высшим членом многочлена 1 будет
a0x1k1-k2(x1x2)k1-k3(x1x2x3)k3-k4…(x1x2…xn-1)Kn-1-Kn(x1x2…xn)Kn = aox1k1x2k2…xnKn .
Отсюда следует, что при вычитании 1 из f высшие члены этих многочленов взаимно уничтожатся, т.е. высший член симметрического многочлена f-1 = f1 будет ниже члена (2), высшего в многочлене f. Повторяя для многочлена fi этот же прием, мы придем к равенству
f1 = 2+f2
где 2 есть произведение степеней элементарных симметрических многочленов, а f2 – симметрический многочлен , высший член которого ниже, чем высший член в f1. Отсюда вытекает равенство
f = 1+2+f2
Продолжая этот процесс, мы для некоторого s получим fs = 0 и поэтому придем к выражению для f в виде многочлена от 1,2,…,n:
s
f(x1,x2,…,xn) = I = (1,2,…,n ) .
I=1
В самом деле, если бы этот процесс был бесконечным, то мы получили бы бесконечную последовательность симметрических многочленов
f1,f2,…,fs,…, (6)
причем высший член каждого из них был бы ниже, чем высшие члены предшествующих многочленов, и тем более ниже, чем (2). Однако, если
bx1l1x2l2…xnln (7)
есть высший член многочлена fs то из симметричности этого многочлена следуют неравенства
l1 l2 … ln , (8)
подобные неравенствам (3). С другой стороны, так как член (2) выше члена (7), то
k1 l1 (9)
Легко заметить ,что системы целых неотрицательных чисел l1,l2, … ,ln удовлетворяющих неравенствам (8) и (9), можно выбрать лишь конечным числом способов.
Действительно, если даже отказаться от требования (8) и лишь предполагать, что все li будет возможен лишь (k1 + 1)n способами. Отсюда следует, что последовательность многочленов (6) со строго понижающимися высшими членами не может быть бесконечной . Теорема доказана.
Рассмотрим некоторые возможные применения этой теоремы.
Метод решения симметрических систем состоит в представлении симметрических многочленов через многочлены от основных симметрических многочленов.
x2 + y2 = (x + y)2 – 2xy ,
x3 + y3 = (x + y)3 - 3xy (x + y),
x2 + y2 + z2 = (x + y + z)2 – 2 (xy + yz +zx).
Заключение
Таким образом, чтобы понять всю силу теоремы Виета, стоит взглянуть на проблемы, представленные в работе. Для сравнения попробуйте решить их по старинке через дискриминант. Вы сразу почувствуете разницу. Я заметила практическое значение теоремы Виета при решении нестандартных уравнений и простейших квадратных уравнений; раскрыты способы «безформального» решения квадратных уравнений.
Мы часто сталкиваемся с уравнениями, для решения которых требуются длительные вычисления, а иногда даже эти вычисления оказываются безуспешными. И как следствие возникает вопрос: можно ли найти простое, рациональное, короткое и элегантное решение этого уравнения? Необходимо помнить, что каждая математическая задача требует индивидуального подхода. Не всегда имеет смысл следовать общим алгоритмам, отклонение от них иногда приводит к более рациональному решению.
Теорема Виета играет большую роль в решении квадратных уравнений. И все же у формул есть преимущество - системы уравнений, связывающие корни уравнений с их коэффициентами. Они там, потому что содержат «подсказку», которая поможет решить некоторые уравнения без формул (но не в вашей голове, это требует большой изобретательности и изобретательности). Полученные от Виета системы уравнений, связывающие корни уравнений любой (не только второй!) Степени с их коэффициентами, теперь называются теоремой Виета, и это имя сегодня знает каждый студент. Какая большая честь для ученого! Какая поистине вечная память и слава! Об этом стоит подумать ... Исследования Виета дали совершенно новое направление работе его современников, а его алгебраические идеи оказали сильное влияние на европейскую науку, он прославился обобщающей алгеброй.
Список использованной литературы
1.Гальперин Г.А., Толпыго А.К., “Московские математические олимпиады”, М., “Просвещение”, 1986 .- 376 с.
2.Готман Э.Г., Скопець З.А., “Задача одна – решения разные”, К., Родник 1938 .- 265 с.
3.Горнштейн П.И., “Задачи с параметрами”, К., 1999 .- 398 с.
4. Фирсова В.В., “Избранные вопросы математики”, М., “Просвещение”, 1990. - 187 с.







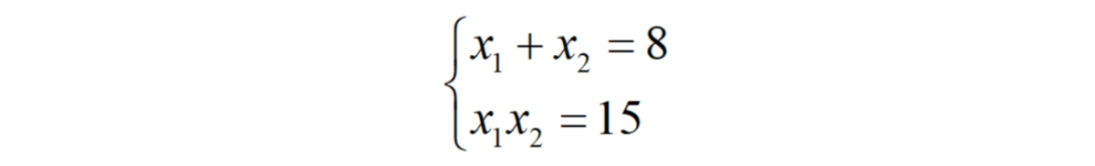
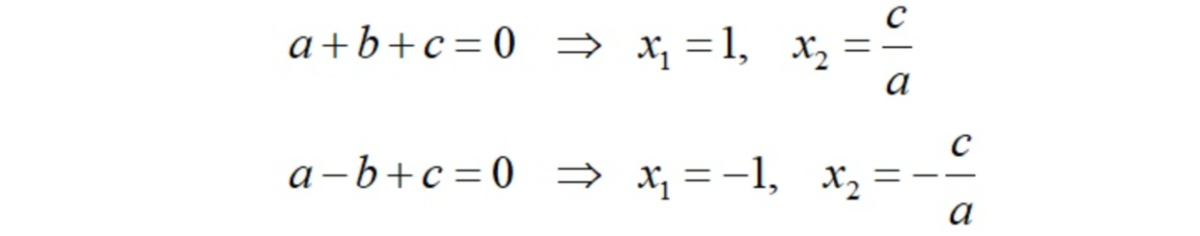
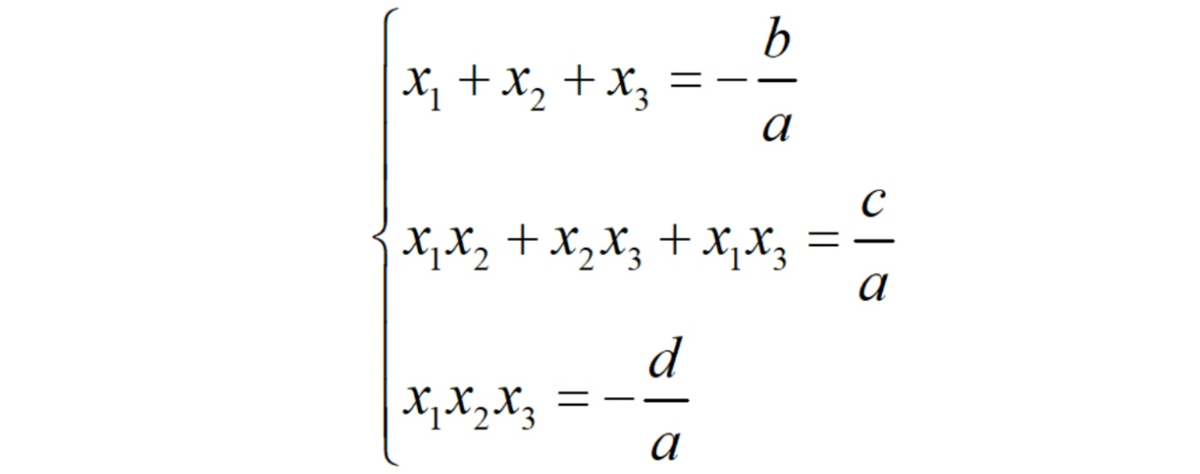
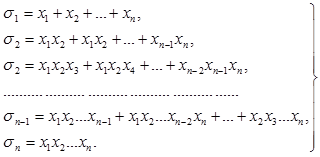 (1)
(1)
















