ОГБПОУ «НОВГОРОДСКИЙ АГРОТЕХНИЧЕСКИЙ ТЕХНИКУМ»
Инструкционная карта на выполнение
Практического занятия № 5 по дисциплине
«Математика»
Тема: Производная функции нескольких переменных
Наименование работы:. Нахождение частных производных функции нескольких переменных. Применение производной к исследованию функций нескольких переменных
| Наименование объектов контроля и оценки | Основные показатели оценки результата |
| Умения: Решать прикладные задачи в области профессиональной деятельности. Знания: Значение математики в профессиональной деятельн ости и при освоении ППССЗ; Основные математические методы решения прикладных задач в области профессиональной деятельности; Основы интегрального и дифференциального исчисления | Оценка результатов выполнения практических работ
|
Норма времени: 4 часа;
Условия выполнения: учебный кабинет;
Оснащение рабочего места: инструкционная карта, калькулятор
Правила по технике безопасности: С правилами техники безопасности на рабочем месте ознакомлены;
Литература: Хрипунова М.Б. Высшая математика. Учебник и практикум для спо М.:Юрайт.2018г.-474с
Уровни усвоения: 1 – 4 задания – 2 уровень
Домашнее, самостоятельное задание – 3 уровень
Теоретическая часть.
1.Частные производные первого порядка
Определение. Если существует конечный предел отношения частного приращения по х функции z=f(x;y) в точке М0(х0;у0) к приращению  , то этот предел называется частной производной по х функции z=f(x;y) в точке М0 и обозначается одним из символов:
, то этот предел называется частной производной по х функции z=f(x;y) в точке М0 и обозначается одним из символов: 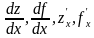
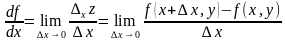
Аналогично частная производная по у от функции z=f(x;y) определяется как предел отношения частного приращения функции у к приращению 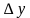 при стремлении
при стремлении 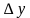 к нулю. Частная производная по у обозначается одним из символов:
к нулю. Частная производная по у обозначается одним из символов: 

Пример. Вычислить частные производные следующих функций: 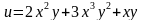




2. Частные производные высших порядков.
Определение. Частными производными второго порядка от функции z=f(x;y) называются частные производные от функций  Общее число вторых производных от функции двух переменных – четыре, так как каждую производную можно продифференцировать как по х, так и по у.
Общее число вторых производных от функции двух переменных – четыре, так как каждую производную можно продифференцировать как по х, так и по у.
Пример. Найти вторые частные производные от функции 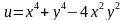
Сначала находим первые частные производные:


Находим вторые производные:




3. Экстремум функции нескольких переменных.
Теорема. (необходимое условие экстремума). Если функция u=f(M) непрерывна в некоторой области D и во внутренней точке М0 области D имеет экстремум, то в этой точке все ее частные производные первого порядка или не существуют, или обращаются в нуль.
Точки, в которых частные производные не существуют, или равны нулю, называются критическими точками функции.
Рассмотрим функцию двух переменных. Обозначим значения вторых частных производных в точке
М0(х0,у0) через А, В, С.

Достаточные условия экстремума. Пусть в некоторой области, содержащей точку М0(х0,у0), функция u=f(x,y) непрерывна со своими частными производными до третьего порядка включительно и пусть М0(х0,у0) - критическая точка функции f(x,y), т.е.  . Тогда в точке М0:
. Тогда в точке М0:
Функция u=f(x,y) имеет максимум, если АС-В20, А
Функция u=f(x,y) имеет минимум, если АС-В20, А0;
Функция u=f(x,y) не имеет экстремума, если АС-В2
Если АС-В2=0, то требуются дополнительные исследования, т.к. в этом случае функция может иметь, а может не иметь экстремума.
Пример. Исследовать на экстремум функцию 
Решение:
Находим первые частные производные и приравниваем их к нулю.


После решения уравнений мы нашли точки, подозреваемые на экстремум:
Вычисляем вторые частные производные в точках, подозреваемых на экстремум:
Проверяем выполнение достаточных условий экстремума:
В точке , - функция имеет минимум
В точке - функция не имеет экстремума
Практическая часть.
Найти частные производные первого порядка:
а) б)
Найти частные производные функции  в точке
в точке 
Найти частные производные второго порядка для функций. Покажите, что 
а)  б)
б)
Исследовать функции на экстремум.
а)  б)
б) 
Домашнее задание:
Найти частные производные второго порядка функции
Исследовать функцию на экстремум:
Самостоятельная работа:
1 вариант.
Найти частные производные второго порядка функции
Исследовать функцию на экстремум:
2 вариант.
Найти частные производные второго порядка функции
Исследовать функцию на экстремум:
Критерии оценки:
«5» - Правильно решены 2 задания.
«4» - Правильно решено 1-е задание, второе выполнено не до конца, либо допущена одна вычислительная ошибка.
«3» - Правильно решено 1 задание.
«2» - Одно задание выполнено, но с ошибками; либо не выполнено ничего







 , то этот предел называется частной производной по х функции z=f(x;y) в точке М0 и обозначается одним из символов:
, то этот предел называется частной производной по х функции z=f(x;y) в точке М0 и обозначается одним из символов: 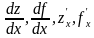
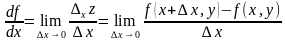
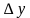 при стремлении
при стремлении 

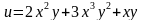




 Общее число вторых производных от функции двух переменных – четыре, так как каждую производную можно продифференцировать как по х, так и по у.
Общее число вторых производных от функции двух переменных – четыре, так как каждую производную можно продифференцировать как по х, так и по у.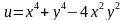







 . Тогда в точке М0:
. Тогда в точке М0:




















