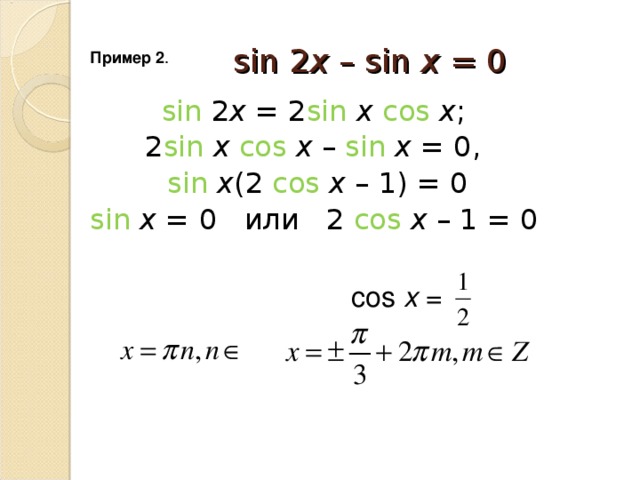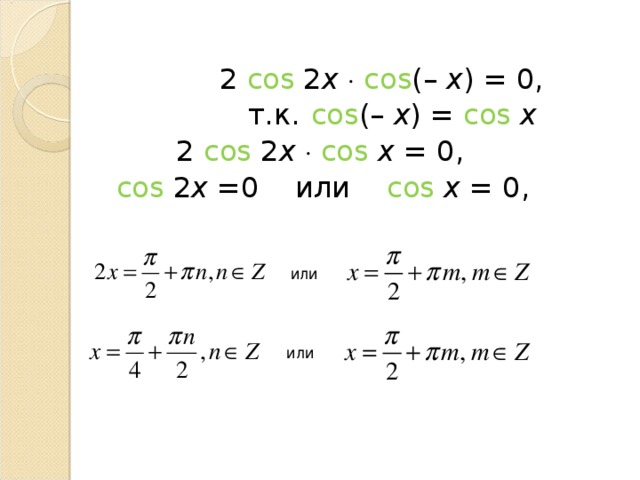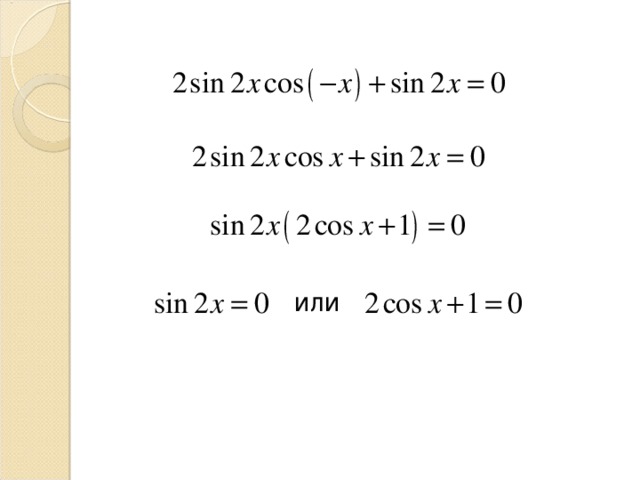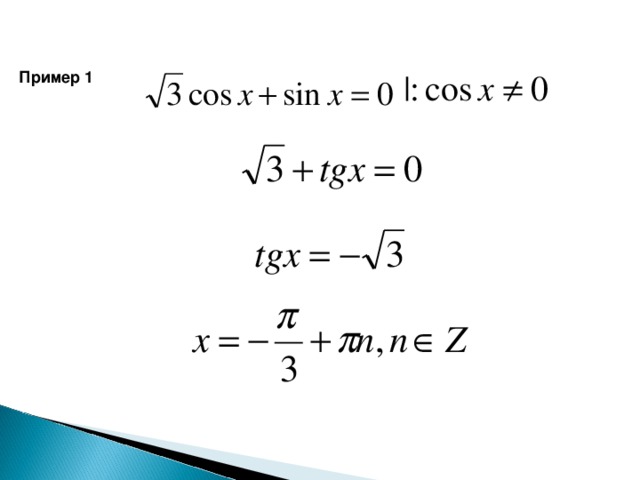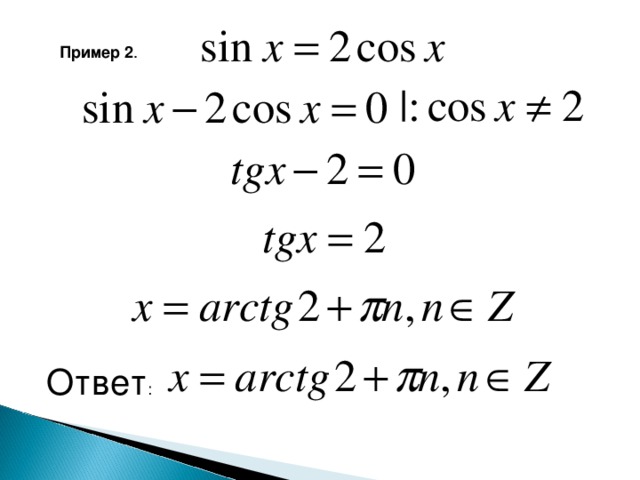Проект:"Методы решения тригонометрических уравнений"

МКОУ «СОШ» с.п. Светловодское

Исследовательский проект

Эпиграф:

Метод решения хорош, если с самого начала мы можем предвидеть – и впоследствии подтвердить это, – что следуя этому методу, мы достигнем цели.

Лейбниц

Немного истории…

На раннем этапе тригонометрия развивалась в тесной связи с астрономией и являлась её вспомогательным разделом.

Астрономы при нахождении расстояний до планет и звёзд использовали свойства треугольника.

Так возникла наука тригонометрия - наука об измерении треугольников, о выражении сторон через его углы.

Хотя название науки возникло сравнительно недавно, многие относимые сейчас к тригонометрии понятия и факты были известны ещё две тысячи лет назад.

Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом (2 в. до н. э.) и Клавдием Птолемеем (2 в. н. э.). Позднее зависимости между отношениями сторон треугольника и его углами начали называть тригонометрическими функциями .

Долгое время тригонометрия носила чисто геометрический характер, т. е. Факты, которые мы сейчас формулируем в терминах тригонометрических функций, формулировались и доказывались с помощью геометрических понятий и утверждений. Такою она была еще в средние века, хотя иногда в ней использовались и аналитические методы, особенно после появления логарифмов .

Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, электричества, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т. д. Поэтому тригонометрические функции всесторонне и глубоко исследовались, и приобрели важное значение для всей математики.

Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком XVIII веке Леонардом Эйлером (1707-1783) членом Петербургской Академии наук. Именно Эйлер первым ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения. После Эйлера тригонометрия приобрела форму исчисления: различные факты стали доказываться путем формального применения формул тригонометрии, доказательства стали намного компактнее, проще.

Таким образом, тригонометрия, возникшая как наука о решении треугольников, со временем развилась и в науку о тригонометрических функциях.

Тригонометрическим уравнением

называется уравнение, в котором

переменная является аргументом

одной или нескольких

тригонометрических функций.

простейшие тригонометрические уравнения

Метод решения

С помощью числовой

окружности

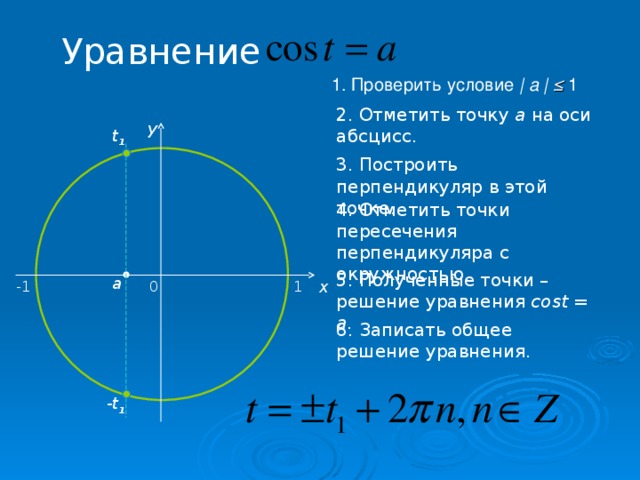
Уравнение

1 . Проверить условие | a | ≤ 1

2 . Отметить точку а на оси абсцисс .

y

t 1

3 . Построить перпендикуляр в этой точке .

4 . Отметить точки пересечения перпендикуляра с окружностью .

5 . Полученные точки – решение уравнения cost = a.

a

x

0

-1

1

6 . Записать общее решение уравнения .

-t 1

Частные случаи уравнения

Π 2

y

π

0

x

0

-1

1

π 2

Уравнение

1 . Проверить условие | a | ≤ 1

2 . Отметить точку а на оси ординат .

y

1

3 . Построить перпендикуляр в этой точке .

-t 1

t 1

4 . Отметить точки пересечения перпендикуляра с окружностью .

a

5 . Полученные точки – решение уравнения sint = a.

x

0

6 . Записать общее решение уравнения .

x=(-1) k arcsina+  k, k  Z

-1

Частные случаи уравнения

Π 2

y

1

π

0

x

0

П 2

-1

« Метод замены переменой»

При решении уравнений указанного типа в основном применяются следующие тригонометрические тождества:

Основное тригонометрическое тождество: следствия:

Косинус двойного аргумента :

Метод решения - замена переменной

• Сделайте замену переменной.
• Решите полученное алгебраическое уравнение относительно новой переменной.
• Сделайте обратную замену и получите совокупность простейших тригонометрических уравнений .

• Уравнения, сводящиеся к квадратным, относительно

cos х = t , sin х = t .

A sin 2 x + B cosx + C = 0

A cos 2 x + В sinx + C = 0

• A sin 2 x + B cosx + C = 0 A cos 2 x + В sinx + C = 0
• A sin 2 x + B cosx + C = 0 A cos 2 x + В sinx + C = 0

Решаются методом введения новой переменной.

Пример 1 .

Пусть

тогда

не удовлетворяет условию

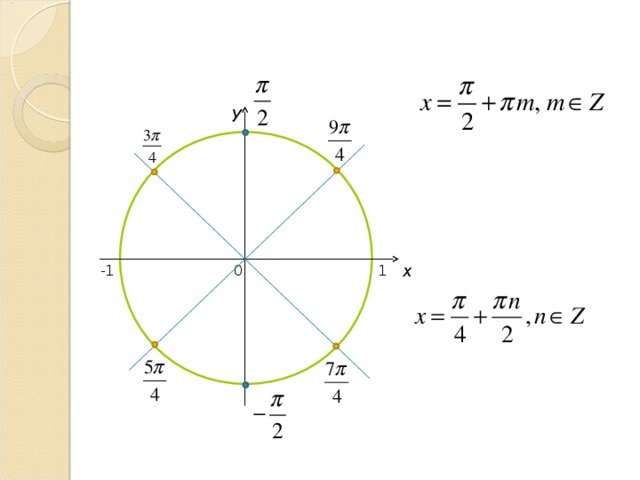
Пример 2 . Решить уравнение

2 sin 2 x + sinx - 1 = 0.

Решение.

Введём новую переменную t = sinx. Тогда данное уравнение примет вид 2 t 2 + t - 1 = 0.

Решим его: D = 1 + 8 = 9,

Cледовательно,

sinx = 1/2 или sinx = -1.

1) sinx = 1/2,

2) sinx = -1,

Пример 3 . Решить уравнение

6 sin 2 x + 5 cosx - 2 = 0.

Решение.

Заменяя sin 2 x на 1-с os 2 x , получим квадратное уравнение относительно с osx .

6 ( 1- cos 2 x ) + 5 cosx - 2 = 0,

-6 cos 2 x + 5cosx + 4 = 0,

6 cos 2 x - 5cosx - 4 = 0.

Пусть cos x = t , тогда 6t 2 - 5t - 4 = 0,

t 1 = - 1/2, t 2 = 4/3.

1." width="640"

Cледовательно, с os x = - 1/2 или cos x = 4/3 .

Решая уравнение с os x = -1/2 , находим:

Уравнение cos x = 4/3 не имеет решений, так как 4 /3 1.

Пример 4 . Решить уравнение

tgx + 2ctgx = 3.

Решение.

Поскольку ctgx =

то уравнение можно записать в виде:

Обозначим tgx через t . Получим уравнение

которое приводится к квадратному t 2 - 3t + 2 = 0,

t 2 - 3t + 2 = 0.

По теореме, обратной теореме Виета,

t 1 = 2, t 2 =1.

Желаю творческих успехов!

Спасибо за внимание!

МКОУ «СОШ» с.п. Светловодское

Исследовательский проект

Тригонометрические уравнения, решаемые разложением на множители

Эпиграф:

• «Уравнение – это золотой ключ, открывающий все

Математические сезамы».

С. Коваль.

Определение

• Уравнение, содержащее неизвестное под знаком тригонометрической функции, называется тригонометрическим . 

Формулы двойного аргумента

• sin 2 x = 2 sin x cos x ,
• cos 2 x = cos 2 x – sin 2 x

Формулы суммы и разности синусов и косинусов

Уравнения, допускающие разложение на множители

основной метод решения:

• основной метод решения:

• Используя метод группировки, разложить одночлены, входящие в состав уравнения, на множители. Используя условие равенства произведения нулю, получите и решите совокупность простейших тригонометрических уравнений.
• Используя метод группировки, разложить одночлены, входящие в состав уравнения, на множители.
• Используя условие равенства произведения нулю, получите и решите совокупность простейших тригонометрических уравнений.

Уравнения, решаемые разложением на множители

cos 2 x – cos x = 0

cos x ( cos x – 1) = 0

cos x = 0 или cos x – 1 =0

cos x = 0 или cos x =1

или

Пример 1 .

sin 2 x – sin x = 0

Пример 2 .

sin 2 x = 2 sin x cos x ;

2 sin x cos x – sin x = 0,

sin x (2 cos x – 1) = 0

sin x = 0 или 2 cos x – 1 = 0

cos x =

Если в уравнении встречаются тригонометрические функции с разными, но кратными аргументами х, 2х, 4х , … , то

• Приведите все аргументы к одинаковым, используя тождества двойного аргумента и / или тождества понижения степени.
• Решите полученное уравнение с одинаковыми функциями одинаковых аргументов

Пример 3 . cos x + cos 3 x = 0

Для решения этого уравнения необходимо вспомнить формулу суммы косинусов

 = х ,  = 3 х ,

2 cos 2 x  cos (– x ) = 0,

т.к. cos (– x ) = cos x

2 cos 2 x  cos x = 0,

cos 2 x =0 или cos x = 0,

или

или

y

x

0

1

-1

Нанесем эти решения единичную окружность и убедимся, что вторая серия корней полностью входит в первую, поэтому в ответе достаточно записать только первую серию корней.

Ответ

Пример 4 . sin x + sin 2 x + sin 3 x = 0

или

Ответ :

Пример 5 . sin 2 x = cos 3 x

или

или

Ответ:

Пример 6 . 2 sin x cos 2 x – 1 + sin x – 2 cos 2 x = 0

или

или

или

Ответ:

Пример 7 . sin 4 x + sin 2 2 x = 0

или

МКОУ «СОШ» с.п. Светловодское

Исследовательский проект

.

Тригонометрия (от греч. trigonon -треугольник и metrio- измеряю) – раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии. Возникла и развивалась в древности как один из разделов астрономии, как ее вычислительный аппарат, отвечающий практическим нуждам человека. С ее помощью можно определить расстояние до недоступных предметов и, вообще, существенно упрощать процесс геодезической съемки местности для составления географических карт. Общепринятые понятия тригонометрии, а также обозначения и определения тригонометрических функция сформировались в процессе долгого исторического развития.

Тригонометрические сведения были известны древним вавилонянам и египтянам, но основы этой науки заложены в Древней Греции встречающиеся уже в III веке до н.э. в работах великих математиков– Евклида, Архимеда, Апполония Пергского.. Древнегреческие астрономы успешно решали отдельные вопросы из тригонометрии, связанные с астрономией. Однако они рассматривали не линии синуса, косинуса и др., а хорды. Роль линии синусов угла a у них выполняла хорда, стягивающая дугу, равную 2 a .

В IV-V веках появился уже специальный термин в трудах по астрономии великого индийского учёного Ариабхаты. Отрезок CB он назвал ардхаджива (ардха –половина, джива – тетива лука, которую напоминает хорда). Позднее появилось более краткое название джива. Арабскими математиками в IX веке это слово было заменено на арабское слово джайб (выпуклость). При переводе арабских математических текстов в веке оно было заменено латинским синус (sinus –изгиб, кривизна). Известный Мухаммед ибн Муса ал-Хорезми ( IX в.) составил таблицы синусов и котангенсов. Ал-Хабаш вычислил таблицы для тангенса, котангенса и косеканса. Слово косинус намного моложе. Косинус – это сокращение латинского выражения completely sinus, т. е. “дополнительный синус” (или иначе “синус дополнительной дуги”).

• В IV-V веках появился уже специальный термин в трудах по астрономии великого индийского учёного Ариабхаты. Отрезок CB он назвал ардхаджива (ардха –половина, джива – тетива лука, которую напоминает хорда). Позднее появилось более краткое название джива. Арабскими математиками в IX веке это слово было заменено на арабское слово джайб (выпуклость). При переводе арабских математических текстов в веке оно было заменено латинским синус (sinus –изгиб, кривизна). Известный Мухаммед ибн Муса ал-Хорезми ( IX в.) составил таблицы синусов и котангенсов. Ал-Хабаш вычислил таблицы для тангенса, котангенса и косеканса. Слово косинус намного моложе. Косинус – это сокращение латинского выражения completely sinus, т. е. “дополнительный синус” (или иначе “синус дополнительной дуги”).

Название «тангенс», происходящее от латинского tanger (касаться), появилось в 1583 г. Tangens переводится как «касающийся» (линия тангенсов – касательная к единичной окружности). Тангенсы возникли в связи с решением задачи об определении длины тени. Тангенс (а также котангенс) введен в X веке Аль - Батани (850-929) и Абу-ль-Вефа Мухамед-бен Мухаммед (940-998), который составил таблицы синусов и тангенсов через 10’ с точностью до 1/604.

Однако эти открытия долгое время оставались неизвестными европейским ученым, и тангенсы были заново открыты лишь в XIV веке немецким математиком, астрономом Региомонтаном (1467 г.). Именно он доказал теорему тангенсов (латинизированное имя немецкого астронома и математика Иоганна Мюллера (1436-1476). Региомонтан составил также подробные тригонометрические таблицы; благодаря его трудам плоская и сферическая тригонометрия стала самостоятельной дисциплиной и в Европе. Региомонтан – самый видный европейский представитель этой эпохи в области тригонометрии. Его обширные таблицы синусов через 1 ’ с точностью до 7-й значащей цифры и его мастерски изложенный тригонометрический труд «пять книг о треугольниках всех видов» имели большое значение для дальнейшего развития тригонометрии в XVI – XVII веках.

• Название «тангенс», происходящее от латинского tanger (касаться), появилось в 1583 г. Tangens переводится как «касающийся» (линия тангенсов – касательная к единичной окружности). Тангенсы возникли в связи с решением задачи об определении длины тени. Тангенс (а также котангенс) введен в X веке Аль - Батани (850-929) и Абу-ль-Вефа Мухамед-бен Мухаммед (940-998), который составил таблицы синусов и тангенсов через 10’ с точностью до 1/604. Однако эти открытия долгое время оставались неизвестными европейским ученым, и тангенсы были заново открыты лишь в XIV веке немецким математиком, астрономом Региомонтаном (1467 г.). Именно он доказал теорему тангенсов (латинизированное имя немецкого астронома и математика Иоганна Мюллера (1436-1476). Региомонтан составил также подробные тригонометрические таблицы; благодаря его трудам плоская и сферическая тригонометрия стала самостоятельной дисциплиной и в Европе. Региомонтан – самый видный европейский представитель этой эпохи в области тригонометрии. Его обширные таблицы синусов через 1 ’ с точностью до 7-й значащей цифры и его мастерски изложенный тригонометрический труд «пять книг о треугольниках всех видов» имели большое значение для дальнейшего развития тригонометрии в XVI – XVII веках.

Однородные уравнения

Сумма показателей степеней при sin x и cos x

у всех слагаемых такого уравнения равна n.

Разделим на .

Получим:

• Уравнение вида asinx + bcosx = 0 называют однородным тригонометрическим уравнением первой степени.
• Уравнение вида a sin 2 x + b sinx cosx + c cos 2 x = 0 называют однородным тригонометрическим уравнением второй степени

Алгоритм решения однородного тригонометрического уравнения

первой степени:

• Деление обеих частей уравнения на cosx , cosx ≠ 0

Алгоритм решения однородного тригонометрического уравнения второй степени:

• Посмотреть, есть ли в уравнении член a sin 2 x .
• Если член a sin 2 x в уравнении содержится (т.е. а ≠ 0), то уравнение решается делением обеих частей уравнения на cos 2 x и последующим введение новой переменной.
• Если член a sin 2 x в уравнении не содержится (т.е. а = 0), то уравнение решается методом разложения на множители: за скобки выносят cosx .

Если тригонометрическое уравнение является однородным уравнением относительно синуса и косинуса одинаковых аргументов, то

1. Проверьте является ли решение

уравнения cosx = 0 решением

заданного уравнения.

Если является, то запишите это решение.

2. Разделите уравнение почленно на

косинус в степени уравнения.

3. Замените sin x/cos x = tgx.

4. Решите полученное уравнение с

одинаковыми функциями одинаковых аргументов

Заданное уравнение можно привести к однородному уравнению с помощью тригонометрического разложения единицы:

1 = sin 2 x + cos 2 x

1 = (sin 2 x + cos 2 x) 2

1 = (sin 2 x + cos 2 x) 3 ...

1. первой степени

|:cos x

a +b =0

tg x=

x= arctg ( ) + π k, k Z

Формулы двойного аргумента

sin 2 x = 2 sin x cos x

cos 2 x = cos 2 x – sin 2 x, или

cos 2 x = 1 – 2 sin 2 x и

cos 2 x = 2 cos 2 x – 1.

Пример 1

Пример 2 .

Ответ :

Пример 3 .

2. второй степени

|:

a +b +c =0

a +b +c =0

a + b +c =0

Пример 4 .

Пусть

тогда

или

или

Пример 5 .

Пусть

тогда

или

Пример 6 .

Пусть тогда

или

Пример 7 .

Пусть тогда

или

Пример 8 .

Пусть тогда

или

Методы решения тригонометрических уравнений

Методы решения тригонометрических уравнений

• Решение тригонометрического уравнения состоит из двух этапов:  преобразование уравнения для получения его простейшего вида ( см. выше ) и  решение полученного простейшего тригонометрического уравнения. Существует семь основных методов решения  тригонометрических уравнений.
•  
• 1. Алгебраический метод.   Этот метод нам хорошо известен из алгебры
•    ( метод замены переменной и подстановки ).

2. Разложение на множители.  Этот метод рассмотрим на примерах

П р и м е р  1.  Решить уравнение:  sin x + cos x = 1 .

Р е ш е н и е .   Перенесём все члены уравнения влево:

     sin x + cos x – 1 = 0 ,

преобразуем и разложим на множители выражение в

  левой части уравнения:

П р и м е р   2

•    Решить уравнение:  cos 2 x + sin x · cos x = 1.

Р е ш е н и е .     cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 ,

  sin x · cos x – sin 2 x = 0 ,

    sin x · ( cos x – sin x ) = 0 ,

П р и м е р   3

Решить уравнение:  cos 2 x – cos 8 x + cos 6 x = 1. 

  Р е ш е н и е .    cos 2 x + cos 6 x = 1 + cos 8 x ,

   2 cos 4 x cos 2 x = 2 cos ² 4 x ,

cos 4 x · ( cos 2 x –  cos 4 x ) = 0 ,

  cos 4 x · 2 sin 3 x · sin x = 0 ,

   1).  cos 4 x = 0 ,               2).  sin 3 x = 0 ,          3). sin x = 0 ,

3. Приведение к однородному уравнению

Уравнение называется однородным относительно  sin   и  cos , если все его члены одной и той же степени относительно sin   и cos   одного и того же угла . Чтобы решить однородное уравнение, надо:

•    а )  перенести все его члены в левую часть;
•     б )  вынести все общие множители за скобки;
•    в )  приравнять все множители и скобки нулю;
•    г )  скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на 
•          cos ( или sin ) в старшей степени; 
•     д )  решить полученное алгебраическое уравнение относительно tan .
•     П р и м е р .   Решить уравнение:  3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2.
•     Р е ш е н и е .  3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x ,
•                               sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 ,
•                              tan 2 x + 4 tan x + 3 = 0 ,  отсюда  y 2 + 4 y +3 = 0 ,
•                              корни этого уравнения:  y 1 = -1,  y 2 = -3,  отсюда
•                              1)   tan x = –1,                  2)   tan x = –3,

4. Переход к половинному углу

Рассмотрим этот метод на примере:

    П р и м е р .  Решить уравнение:  3 sin x – 5 cos x = 7. 

   Р е ш е н и е .

  6 sin ( x / 2 ) · cos ( x / 2 ) – 5 cos ² ( x / 2 ) + 5 sin ² ( x / 2 ) =  

= 7 sin ² ( x / 2 ) + 7 cos ² ( x / 2 ) ,

2 sin ² ( x / 2 ) – 6 sin ( x / 2 ) · cos ( x / 2 ) + 12 cos ² ( x / 2 ) = 0 ,

     tan ² ( x / 2 ) – 3 tan ( x / 2 ) + 6 = 0 ,

5. Введение вспомогательного угла.

Рассмотрим уравнение вида:

  a sin x + b cos x = c ,

где  a , b , c – коэффициенты;  x – неизвестное.

Теперь коэффициенты уравнения обладают свойствами синуса и косинуса, а именно: модуль ( абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1. Тогда можно обозначить их соответственно как cos и sin ( здесь - так называемый вспомогательный угол ), и наше уравнение принимает вид:

6. Преобразование произведения в сумму

Здесь используются соответствующие формулы.

    П р и м е р .  Решить уравнение:  2 sin x · sin 3 x = cos 4 x .

Р е ш е н и е .  Преобразуем левую часть в сумму:

•                                       cos 4 x – cos 8 x = cos 4 x ,
•  
•                                                  cos 8 x = 0 ,
•  
•                                                  8 x = p / 2 + p k ,
•  
•                                                   x = p / 16 + p k / 8 .

7. Универсальная подстановка

• Рассмотрим этот метод на примере.

Таким образом, решение даёт только первый случай

Учиться можно только

весело…

Чтобы переваривать

знания, надо поглощать

их с аппетитом.

Анатоль Франс

1844 - 1924

Методы р ешени я тригонометрических уравнений

Подготовила учитель математики

МКОУ «СОШ» с.п. Светловодское

Кокова И.В.

Цели урока:

образовательные:

обобщить, систематизировать и углубить имеющиеся у школьников знания о методах решения тригонометрических уравнений.

воспитательные:

- воспитание познавательного интереса к учебному процессу;

- формирование умения анализировать поставленную задачу;

развивающие:

- формировать навык проводить анализ ситуации с последующим выбором наиболее рационального выхода из нее.

Устные упражнения

1.Установите соответствие:

sin x = 0

1

cos x = -1

2

3

sin x = 1

cos x = 1

4

tg x = 1

5

sin x = - 1

6

7

cos x = 0

Установите соответствие:

1

sin x = 0

cos x = -1

2

sin x = 1

3

4

cos x = 1

5

tg x = 1

6

sin x = - 1

7

cos x = 0

Ответьте на вопросы

Какие частные случаи существуют при решении простейших тригонометрических уравнений?

Когда уравнение вида sin  x = a не имеет решений?

Какая из тригонометрических функций четная? Каким свойством обладает график четной функции?

Дайте определение арккосинуса числа x .

Дайте определение арксинуса числа x .

Защита групповых проектов

• 1 группа « Метод замены переменной»;
• 2 группа « Метод разложение на множители»;
• 3 группа « Однородные тригонометрические уравнения».
• Самостоятельная работа.
• Методы решения тригонометрических уравнений.

Три «закона» тригонометрии

• Увидел квадрат – понижай степень.

• Увидел произведение – делай сумму.

• Увидел сумму – делай произведение.

9

Перед вами общая схема решения тригонометрических уравнений.

№ № 164(в), 166(а), 169(а), 174(в), №174.

Домашнее задание: