Программа элективного курса
«Подготовка к ЕГЭ »
Учитель:
Карагаева Татьяна Петровна
Пояснительная записка
Целью профильного обучения, как одного из направлений модернизации математического образования является обеспечение углубленного изучения предмета и подготовка учащихся к продолжению образования. Основным направлением модернизации математического школьного образования является отработка механизмов итоговой аттестации через введение единого государственного экзамена. Появление таких заданий на экзаменах далеко не случайно, т.к. с их помощью проверяется техника владения формулами элементарной математики, методами решения уравнений и неравенств, умение выстраивать логическую цепочку рассуждений, уровень логического мышления учащегося и их математической культуры. Решению задач с параметрами в школьной программе уделяется мало внимания. Большинство учащихся либо вовсе не справляются с такими задачами, либо приводят громоздкие выкладки. Причиной этого является отсутствие системы заданий по данной теме в школьных учебниках. В связи с этим возникла необходимость в разработке и проведении элективного курса для старшеклассников по теме: «Решение задач с параметрами». Многообразие задач с параметрами охватывает весь курс школьной математики. Владение приемами решения задач с параметрами можно считать критерием знаний основных разделов школьной математики, уровня математического и логического мышления. Задачи с параметрами дают прекрасный материал для настоящей учебно-исследовательской работы.
Цель курса
Формировать у учащихся умения и навыки по решению задач с параметрами для подготовки к ЕГЭ и к обучению в ВУЗе.
Изучение курса предполагает формирование у учащихся интереса к предмету, развитие их математических способностей.
Развивать исследовательскую и познавательную деятельность учащихся.
Обеспечить условия для самостоятельной творческой работы.
В результате изучения курса учащийся должен:
усвоить основные приемы и методы решения уравнений, неравенств, систем уравнений с параметрами;
применять алгоритм решения уравнений, неравенств, содержащих параметр;
проводить полное обоснование при решении задач с параметрами;
овладеть исследовательской деятельностью.
Структура курса планирования учебного материала
Темы:
Первоначальные сведения. 2ч
Решения линейных уравнений, содержащих параметры. 2ч
Решения линейных неравенств, содержащих параметры. 2ч
Модуль и параметр. 2ч.
Квадратные уравнения и неравенства, содержащие параметры. 7ч
Свойства квадратичной функции в задачах с параметрами. 4ч
Рациональные уравнения. 2ч
Рациональные неравенства. 2 ч
Иррациональные уравнения. 2ч
Иррациональные неравенства. 2ч
Показательные и логарифмические уравнения, содержащие параметры. 4 ч
Показательные и логарифмические неравенства, содержащие параметры . 4ч
Производная и ее применения. 4ч
Тригонометрия и параметры. 4ч
Графические приемы решения. 4ч
Нестандартные задачи с параметрами. 6ч
количество решений уравнений;
уравнения и неравенства с параметрами с некоторыми условиями.
Текстовые задачи с использованием параметра. 4 ч
Краткое содержание курса
Первоначальные сведения.
Определение параметра. Виды уравнений и неравенств, содержащие параметр.
Основные приемы решения задач с параметрам.
Решение простейших уравнений с параметрами.
Цель: Дать первоначальное представление учащемуся о параметре и помочь привыкнуть к параметру, к необычной форме ответов при решении уравнений.
II. Решение линейных уравнений (и уравнений, приводимых к линейным), содержащих параметр.
Общие подходы к решению линейных уравнений. Решение линейных уравнений, содержащих параметр.
Решение уравнений, приводимых к линейным.
Решение линейно-кусочных уравнений.
Применение алгоритма решения линейных уравнений, содержащих параметр.
Геометрическая интерпретация.
Решение систем уравнений.
Цель: Поиск решения линейных уравнений в общем виде; исследование количества корней в зависимости от значений параметра.
III. Решение линейных неравенств, содержащих параметр.
Определение линейного неравенства.
Алгоритм решения неравенств.
Решение стандартных линейных неравенств, простейших неравенств с параметрами.
Исследование полученного ответа.
Обработка результатов, полученных при решении.
Цель: Выработать навыки решения стандартных неравенств и приводимых к ним, углубленное изучение методов решения линейных неравенств.
IV. Модуль и параметр.
Определение модуля.
Алгоритм решения уравнений и неравенств с модулем.
Раскрытие разных модулей.
Графический способ решения.
Цель: Выработать навыки решения уравнений и неравенств с модулем, содержащих параметр.
V. Квадратные уравнения, содержащие параметр.
Актуализация знаний о квадратном уравнении. Исследования количества корней, в зависимости от дискриминанта. Использование теоремы Виета.
Исследование трехчлена.
Алгоритм решения уравнений.
Графический способ. Аналитический способ решения.
Классификация задач, с позиций применения к ним методов исследования.
Цель: Формировать умение и навыки решения квадратных уравнений с параметрами.
VI. Свойства квадратичной функции в задачах с параметрами.
Область значений функции.
Область определения функции.
Монотонность. Координаты вершины параболы.
Цель: Познакомить с многообразием задач с параметрами, решаемых с помощью свойств квадратичной функции.
VII. Рациональные уравнения.
Общая схема решения целых и дробно-рациональных уравнений.
Решение соответствующих уравнений, содержащих параметр.
Различные способы решения.
Цель: Сформировать умение решать рациональные уравнения с параметром.
Исследование дробно-рациональных уравнений, содержащих параметр.
VIII. Рациональные неравенства.
Общая схема решения, «метод областей».
Различные способы решений.
Цель: Формировать умение и навыки решения рациональных неравенств с параметром.
Иррациональные уравнения.
Схемы решения иррациональных уравнений.
Область определения уравнения.
Решение соответствующих уравнений, содержащих параметр.
Цель: Сформировать умение решать иррациональные уравнения с параметром.
Исследование иррациональных уравнений, содержащих параметр.
Х. Иррациональные неравенства.
Схемы решения иррациональных неравенств.
Решение соответствующих неравенств, содержащих параметр.
Цель: Формировать умение и навыки решения иррациональных неравенств с параметром.
XI. Показательные и логарифмические уравнения, содержащие параметры.
Свойства степеней и показательной функции. Решение показательных уравнений, содержащих параметры.
Свойства логарифмов и логарифмической функции. Решение логарифмических уравнений с параметрами.
Цель: Сформировать умение решать показательные и логарифмические уравнения с параметрами.
XII. Показательные и логарифмические неравенства, содержащие параметры.
Свойства показательной функции. Решение показательных неравенств, содержащих параметры.
Свойства логарифмической функции. Решение логарифмических неравенств с параметрами.
Цель: Формировать умение и навыки решения показательных и логарифмических неравенств с параметром.
XIII. Производная и ее применения.
Касательная к функции.
Критические точки.
Монотонность.
Наибольшие и наименьшие значения функции.
Построение графиков функций.
Цель: Познакомить учащихся с типом задач с параметрами на применение методов дифференциального исчисления.
XIV. Тригонометрия и параметры.
Использование основных свойств тригонометрических функций в задачах с параметрами. Тригонометрические уравнения, содержащие параметр.
Тригонометрические неравенства, содержащие параметр.
Область значений тригонометрических функций.
Цель: Сформировать умение использования свойств тригонометрических функций при решении тригонометрических уравнений и неравенств с параметрами.
XV. Графические приемы решения.
Использование свойств различных функций при решении заданий с параметром.
Специфика решений графическим способом.
Преимущества и недостатки графического способа.
Цель: Научить графическим приемам решения задач с параметром.
XVI. Нестандартные задачи с параметрами.
Использование различных свойств при решении задач с параметрами.
Умение проводить анализ задачи, находить алгоритм решения.
Цель: Формировать навыки исследовательской деятельности, развивать логическое и математическое мышление.
XII. Текстовые задачи с использованием параметра.
Использование различных свойств при решении задач с параметрами.
Умение проводить анализ задачи, находить алгоритм решения.
Цель: Формировать навыки исследовательской деятельности, развивать логическое и математическое мышление.
Планирование (64 часа)
| № урока | Тема | Дата проведения |
| 1 | Основные понятия уравнений с параметрами |
|
| 2 | Основные понятия неравенств с параметрами |
|
| 3 | Решение линейных уравнений с параметрами |
|
| 4 | Решение линейных уравнений с параметрами |
|
| 5 | Решение линейных неравенств с параметрами |
|
| 6 | Решение линейных неравенств с параметрами |
|
| 7 | Модуль и параметр |
|
| 8 | Модуль и параметр |
|
| 9 | Квадратные уравнения, содержащие параметр |
|
| 10 | Квадратные уравнения, содержащие параметр |
|
| 11 | Квадратные уравнения, содержащие параметр |
|
| 12 | Квадратные уравнения, содержащие параметр |
|
| 13 | Квадратные неравенства, содержащие параметр |
|
| 14 | Квадратные неравенства, содержащие параметр |
|
| 15 | Квадратные неравенства, содержащие параметр |
|
| 16 | Свойства квадратичной функции |
|
| 17 | Свойства квадратичной функции |
|
| 18 | Свойства квадратичной функции |
|
| 19 | Свойства квадратичной функции |
|
| 20 | Рациональные уравнения с параметром |
|
| 21 | Рациональные уравнения с параметром |
|
| 22 | Рациональные неравенства с параметрами |
|
| 23 | Рациональные неравенства с параметрами |
|
| 24 | Иррациональные уравнения с параметром |
|
| 25 | Иррациональные уравнения с параметром |
|
| 26 | Иррациональные неравенства с параметрами |
|
| 27 | Иррациональные неравенства с параметрами |
|
| 28 | Показательные уравнения с параметром |
|
| 29 | Показательные уравнения с параметром |
|
| 30 | Логарифмические уравнения с параметром |
|
| 31 | Логарифмические уравнения с параметром |
|
| 32 | Показательные неравенства с параметром |
|
| 33 | Показательные неравенства с параметром |
|
| 34 | Логарифмические неравенства с параметром |
|
| 35 | Логарифмические неравенства с параметром |
|
| 36 | Производная и ее применения |
|
| 37 | Производная и ее применения |
|
| 38 | Производная и ее применения |
|
| 39 | Производная и ее применения |
|
| 40 | Параметры в тригонометрии |
|
| 41 | Параметры в тригонометрии |
|
| 42 | Параметры в тригонометрии |
|
| 43 | Параметры в тригонометрии |
|
| 44 | Графические приемы решения |
|
| 45 | Графические приемы решения |
|
| 46 | Графические приемы решения |
|
| 47 | Графические приемы решения |
|
| 48 | Количество решений уравнений |
|
| 49 | Количество решений уравнений |
|
| 50 | Уравнения и неравенства с параметрами с различными условиями |
|
| 51 | Уравнения и неравенства с параметрами с различными условиями |
|
| 52 | Уравнения и неравенства с параметрами с различными условиями |
|
| 53 | Уравнения и неравенства с параметрами с различными условиями |
|
| 5 | Текстовые задачи с использованием параметра |
|
| 55 | Текстовые задачи с использованием параметра |
|
| 56 | Текстовые задачи с использованием параметра |
|
| 57 | Текстовые задачи с использованием параметра |
|
| 58 | Итоговая контрольная работа по курсу |
|
| 59 | Итоговая контрольная работа по курсу |
|
| 60 – 64 | Защита индивидуальных проектов |
|
Методические рекомендации при изучении некоторых тем
Линейные и квадратные уравнения
Линейное уравнение, записанное в общем виде, можно рассматривать как уравнение с параметрами: ах = b, где х – неизвестное, а, b – параметры. Для этого уравнения особым или контрольным значением параметра является то, при котором обращается в нуль коэффициент при неизвестном.
При решении линейного уравнения с параметром рассматриваются случаи, когда параметр равен своему особому значению и отличен от него.
Особым значением параметра а является значение а = 0.
1. Если а ≠ 0 , то при любой паре параметров а и b оно имеет единственное решение х = 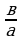 .
.
2. Если а = 0, то уравнение принимает вид: 0 х = b. В этом случае значение b = 0 является особым значением параметра b.
2.1. При b ≠ 0 уравнение решений не имеет.
2.2. При b = 0 уравнение примет вид: 0 х = 0. Решением данного уравнения является любое действительное число.
Пример. Решить уравнение
2а(а — 2) х = а — 2. (1)
Решение. Здесь контрольными будут те значения параметра, при которых коэффициент при х обращается в 0. Такими значениями являются а=0 и а=2. При этих значениях а невозможно деление обеих частей уравнения на коэффициент при х. В то же время при значениях параметра а≠0, а≠2 это деление возможно. Таким образом, целесообразно множество всех действительных значений параметра разбить на подмножества
A1={0}, А2={2} и А3= {а≠0, а≠2}
и решить уравнение (1) на каждом из этих подмножеств, т. е. решить уравнение (1) как семейство уравнений, получающихся из него при следующих значениях параметра:
1) а=0 ; 2) а=2 ; 3) а≠0, а≠2.
Рассмотрим эти случаи.
1) При а=0 уравнение (1) принимает вид 0 х = - 2. Это уравнение не имеет корней.
2) При а=2 уравнение (1) принимает вид 0 х=0. Корнем этого уравнения является любое действительное число.
3) При а≠0, а≠2 из уравнения (1) получаем, х = 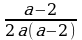 ,
,
откуда х = 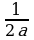 .
.
0твет: 1) Если а=0,то корней нет;
2)если а=2, то х – любое действительное число;
3) если а≠0, а≠2 , то х =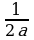 .
.
Свойства квадратичной функции в задачах с параметрами
При решении различных задач часто используются не только свойства квадратного уравнения, но и свойства квадратичной функции. Полезно дать учащимся таблицу, позволяющую составлять систему неравенств для нахождения решений задачи. Обратить внимание, что тогда неравенства составляются в виде  аf(A)или аf(A) 0 (а- старший коэффициент).
аf(A)или аf(A) 0 (а- старший коэффициент).
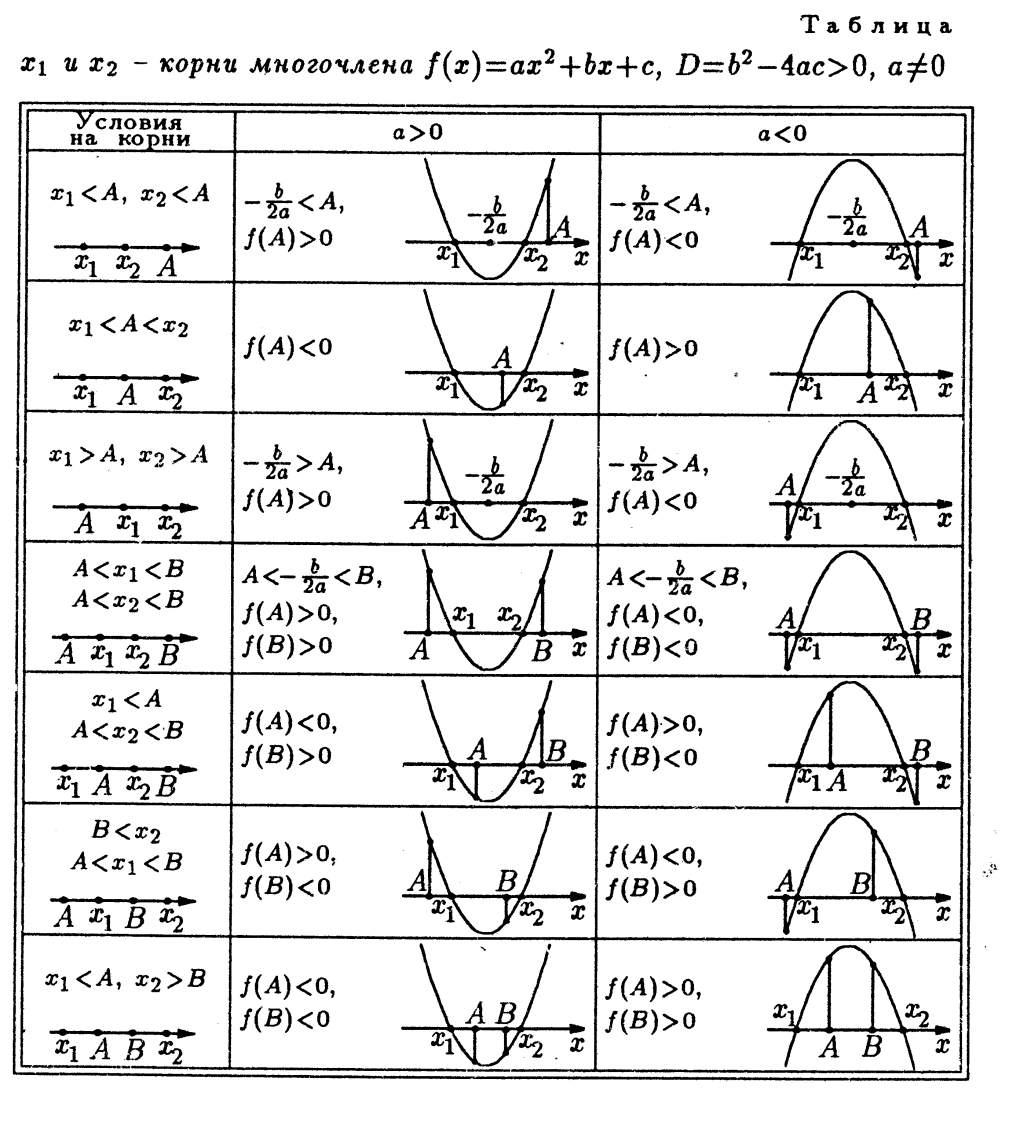
Пример. При каких значениях параметра а один из корней уравнения
(а2-2)х2+(а2+а-1)х-а3+а=0
больше числа а, а другой меньше числа а?
Решение. Задача равносильна следующей: при каких значениях параметра а нули квадратичной функции
g(х)= (а2-2)х2+(а2+а-1)х-а3+а
лежат на вещественной оси по разные стороны от точки х = а?
Исходя из таблицы, имеем условие: аf(A)
В нашем случае это условие принимает вид
(а2-2) g(а)0.
Следовательно, требованию задачи удовлетворяют решения неравенства
(а2-2)((а2-2)а2+(а2+а-1)а-а3+а)а2-2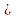 0 (а =
0 (а =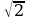 , а =-
, а =-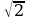 требованию задачи не удовлетворяют).
требованию задачи не удовлетворяют).
Решая полученное неравенство,
находим, что а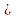 (-
(-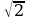 ; -1)
; -1)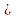 (1;
(1; 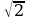 ).
).
Ответ: При а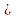 (-
(-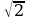 ; -1)
; -1)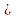 (1;
(1; 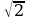 ).
).
Иррациональные уравнения с параметрами
Существует несколько способов решения иррациональных уравнений с параметрами. Познакомимся с ними, разобрав следующий пример.
Пример. В зависимости от значений параметра  решить уравнение
решить уравнение
 (1)
(1)
Решение. Решим уравнение (1) пятью способами, которые необходимо знать, ибо наряду с другими подходами они могут быть использованы и при решении иных типов уравнений.
1.Уравнение (1) равносильно системе
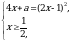
или системе
 (2)
(2)
Решая уравнение из системы (2), находим
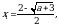
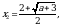 (3)
(3)
откуда следует, что при 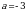 уравнение (1) имеет одно решение
уравнение (1) имеет одно решение  . Если
. Если 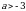 , то
, то  , и тогда уравнение (1) будет иметь два решения при тех значениях параметра
, и тогда уравнение (1) будет иметь два решения при тех значениях параметра  , при которых совместна система
, при которых совместна система
 ,
,
т.е. при 
Уравнение (1) будет иметь только один корень 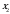 , если
, если 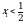 , а
, а  . В этом случае решая систему
. В этом случае решая систему
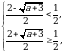
приходим к выводу, что 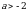 .
.
Замечая теперь, что при  дискриминант уравнения системы (2) отрицателен, получаем
дискриминант уравнения системы (2) отрицателен, получаем
Ответ: если  , то решений нет;
, то решений нет;
если 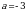 , то
, то  ;
;
если  , то
, то  ;
;
если 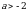 , то
, то  .
.
Заключение
Введение элективного курса «Решение задач с параметрами» необходимо учащимся в наше время как при подготовке к ЕГЭ, так и к вступительным экзаменам в ВУЗы. Владение приемами решения задач с параметрами можно считать критерием знаний основных разделов школьной математики.
Поэтому учащиеся, владеющие методами решения задач с параметрами, успешно справляются (и опыт это подтверждает) с другими задачами. Решение задач, уравнений с параметрами открывает перед учащимися значительное число эвристических приемов общего характера, ценных для математического развития личности, применяемых в исследованиях и на любом другом математическом материале.
При решении задач с параметрами одновременно активно реализуются основные методические принципы:
принцип параллельности – следует постоянно держать в поле зрения несколько тем, постепенно продвигаясь по ним вперед и вглубь;
принцип вариативности – рассматриваются различные приемы и методы решения с различных точек зрения: стандартность и оригинальность, объем вычислительной и исследовательской работы;
принцип самоконтроля – невозможность подстроиться под ответ вынуждает делать регулярный и систематический анализ своих ошибок и неудач;
принцип регулярности – увлеченные математикой дети с удовольствием дома индивидуально исследуют задачи, т. е. занятия математикой становятся регулярными, а не от случая к случаю на уроках.
Разработанный элективный курс может быть использован учителями математики при подготовке к ЕГЭ, вступительным экзаменам в ВУЗы, на занятиях математического кружка.
Список литературы.
Амелькин. В. В., Рабцевич В. Л. Задачи с параметрами. Справочное пособие по математике. – 2-е изд. - Мн. ООО «Асар», 2012. – 464 с.; ил.
Галицкий М. Л. и др. Сборник задач по алгебре для учащихся шк. и кл. с углубл. изуч. математики. – 4-е изд. – Просвещение, 2007. – 271 с.; ил.
Горнштейн П. И., Полонский В. Б., Якир М. С. Задачи с параметрами. – 3-е изд. – М.; Илекса, Харьков: Гимназия, 2008, - 336 с.
Дорофеев Г. В. и др. Математика: Для поступающих в вузы: Пособие. – 5-е изд. – М.: Дрофа, 2010. – 672 с.; ил.
Сканави М. И. и др. Сборник задач по математике для поступающих во втузы. – 7-е изд. – М. 1996. – 528 с.; ил.
Подбор задач с параметрами 7-11 классы.
7 класс
1. При каком значении параметра 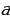 ,
,  является корнем уравнения
является корнем уравнения 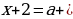 7?
7?
Решение: Так как корень уравнения
корень уравнения 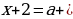 7 , то при подстановке
7 , то при подстановке  в уравнение получим верное равенство
в уравнение получим верное равенство 7 , откуда находим
7 , откуда находим 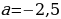 .
.
Ответ: при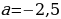 .
.
2. Решить уравнение 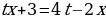
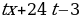
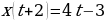
Если 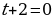 ,
, 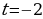 , то уравнение примет следующий вид
, то уравнение примет следующий вид
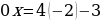 ,
,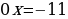 , это уравнение не имеет корней.
, это уравнение не имеет корней.
Если 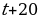 ,
,
Ответ: при 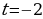 , корней нет;
, корней нет;
при 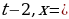
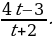
3. Решить уравнение  относительно переменной
относительно переменной 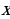 .
.
Решение: Раскроем скобки: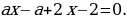
Запишем уравнение в стандартном виде: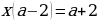 .
.
В случае, если выражение а + 2 не нуль , т. е. если 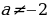 , имеем решение
, имеем решение
 .
.
Если 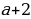 равно нулю, т.е.
равно нулю, т.е. , то имеем равенство
, то имеем равенство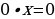 , поэтому
, поэтому
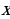 – любое число.
– любое число.
Ответ: при 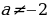
 ;
;
при 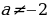
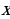 - любое число.
- любое число.
4.Найдите значение коэффициента а в уравнении ах + 5у – 40 = 0, если известно, что решением уравнения является пара чисел:
а) (3; 2); б) (9; -1)
5. Найдите значение коэффициента b в уравнении 6х + bу – 35 = 0, если известно, что решением уравнения является пара чисел:
а) (0; 1); б) (3; 8,5)
6. Найдите значение коэффициента с в уравнении 8х + 3у – с = 0, если известно, что решением уравнения является пара чисел: а) (2; -1); б) (3; 0)
7. При каком значении m решением уравнения mх + 4у – 12 m = 0 является пара чисел: а) (0; 3); б) (12; 0)
8. Дана система уравнений х + ау = 35,bх + 2у = 27.Известно, что пара чисел (5; 6) является её решением, найдите значения а и b.
9. При каком значении р график функции у = рх + 1 пройдёт через точку пересечения прямых 6х – у = 13 и 5х + у = 20 ?
10. При каких значениях р график функции у = р2 – 2рх проходит через точку (-1; 0) ?
8класс
1. При каких значениях параметра а уравнение а(а + 3)х2+2(а + 3) – 3(а + 3) = 0
имеет более одного корня?
Решение.
Рассмотрим три случая.
1). а и а-3
При таких значениях параметра а уравнение будет квадратным. Квадратное уравнение имеет более одного корня ( 2 различных ), когда дискриминант Д0.
Д = 4 ( а +3 )2 + 12а ( а + 3 )2 = 4 ( а + 3 )2( 1 + 3а ) 0.
Решая данное неравенство методом интервалов получаем ано так как а, то получаем, что а.
2). а = 0. Тогда данное уравнение принимает вид 6х – 9 = 0 и имеет только один корень, что не удовлетворяет условию задачи.
3). а= -3. Получаем уравнение 0х2 + 0х + 0 = 0, которое имеет бесконечное множество решений, что удовлетворяет условию задачи.
Ответ: при а ; а = - 3.
2. При каких значениях a уравнение ax2—x+3=0 имеет единственное решение?
Решение.
Ошибочно считать данное уравнение квадратным. На самом деле это уравнение степени не выше второй. Исходя из этого соображения, рассмотрим следующие случаи:
а) a=0. При этом уравнении принимает вид –x+3=0, откуда x=3, т.е. решение единственно.
б) a≠0, тогда ax2—x+3=0 – квадратное уравнение, дискриминант D=1-12a. для того, чтобы уравнение имело единственное решение, нужно чтобы D=0, откуда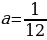
ответ:  или
или 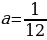
3. при каких значениях a уравнение (a-2)x²+(4-2a)x+3=0 имеет единственное решение?
Решение.
1)При a=2 исходное уравнение не имеет решения.
2) a≠2, тогда данное уравнение является квадратным и принимает вид
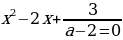
Искомые значения параметра- это корни дискриминанта, который обращается в нуль при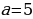
Ответ: 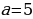
4. Решить уравнение при всех значениях параметра.
c - 2 = x + 2 (Какое значение будет иметь корень уравнения при ?
Ответ: х = с - 4,
5. Решить уравнение при всех значениях параметра.
x + 4 = a - 3 (Выяснить, при каких значениях параметра а корень уравнения равен -7)
Ответ: х = а - 7, х ≠ -7 ⇒ а ≠ 0.
6. Решить уравнение при всех значениях параметра.
b - 8 + 2x = 2b (Выяснить, при каких значениях параметра корень уравнения не равен 4,5)
Ответ:
7. При каких значениях параметра а уравнение (а2 - 6а + 5) = а - 1 имеет
1) один корень;
2) ни одного корня;
3) бесконечно много корней?
Ответ: 1) а ≠ 1; а ≠ 5;
2) а = 5;
3) а = 1.
Решить уравнения при всех значениях параметра (№5 - 6).
8. (2 - х)а = х + 1.
Ответ: а ≠ -1 ⇒x = (2a - 1)/(1+a).
9. (а2 - 1)х = а + 1.
Ответ: а ≠ 1 ⇒ х = 1/(а - 1).
10*. |3x - c| = |x + 2|.
Ответ: с = -6 ⇒x = -2;c ≠ -6 ⇒x1 = 0,5(c + 2), x2 = 0,25(c - 2).
9 класс
1. Найдите все значения параметра а, при которых график функции
у=ах2+2х-а+2 пересекает ось Ох в одной точке.
Решение:1)Если а =0,то у=2х+2—линейная функции, графиком которой является прямая, пересекающая ось Ох в одной точке, т.к. к=2≠0
2)Если а≠0, то у=ах2+2х-а+2 - квадратичная функция, графиком которой является парабола, и пересекающая ось Ох в одной точке, если ув=0
Итак, ув= -(4-4а(-а+2))/4а, ув=0
-(4+4а2-8а)/4а=0,
(4а2-8а+4)/4а=0
Т.к. а ≠ 0, то 4а2-8а+4=0,
а2-2а+1=0,
(а-1)2=0,
а=1.
2. Найдите все значения m, при которых парабола у=х2- х+1 имеет с прямой х + my - 1= 0 одну единственную общую точку.
Решение: Парабола и прямая имеют единственную общую точку, если система y=x2-x+1,x+my -1=0 имеет единственное решение.
Выясним, при каких m это возможно:
y=x2-x+1,
x+my-1=0;
x=1-my,
y=(1-my)2-(1-my)+1.
Преобразуем второе уравнение системы:
у=1-2my+m2y2 - 1+my+1,
m2y2 – (1+m)y+1=0.
Очевидно, что рассматриваемая система имеет единственное решение, если полученное квадратное уравнение имеет единственное решение.
Если m=0, то уравнение примет вид: у+1=0, которое имеет единственное решение и условие задачи выполняется.
Если m ≠ 0, то квадратное уравнение имеет 1 решение, если его D=0
D = (1+m)2- 4m2= 1+2m+m2- 4m2= 1+2m-3m2,
3m2- 2m -1 = 0
Ответ: 0; 1.
3. Найдите все значения а, при которых уравнение |3|x| - a2| =x – a имеет ровно три различных решения. (Ответ: а=-3, а=-1)
4. Найдите все значения а, при каждом из которых уравнение ||x – a| - 2| =x+4 имеет бесконечное число корней. (Ответ: а=-2, а=-6)
Найдите все значения k, при которых прямая y=kx пересекает график функции у= ||2x – 10|-4| в четырех различных точках. (Ответ: 0k
5. Найдите все положительные значения k, при которых прямая y=kx пересекает в двух различных точках ломаную, заданную условиями:
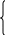 1, если |x|≤ 3
1, если |x|≤ 3
у= -2x-5, если х
2x-5, если x3
(Ответ: 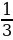 k
k
6.Найдите все значения m, при котором точки А(-3;15), В(9;-5) и С(24;m) лежат на одной прямой. (Ответ: m=-30)
7. Найдите все значения а, при которых точка пересечения прямых у=2х+1 и у=а-5х находится в первой координатной четверти. (Ответ:а1)
8. Парабола у=х2+bx+c, симметричная относительно прямой х=-2, касается прямой у= х+3. Найдите коэффициенты b, c. (Ответ: b=4,c=4)
9. При каких значениях а парабола у=3х2-2ах+4 и прямая у=а-2 не имеют общих точек? (Ответ: -6a
10. Постройте график функции y=f(x), где
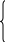 2x2+8x+8, если x
2x2+8x+8, если x
f(x) = |x|+1, если -1≤x≤3
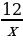 , если x3.
, если x3.
При каких значениях m прямая у=m имеет с графиком этой функции три общих точки. (Ответ: m (0;1)∪(2;4))
10-11 класс
1. При каких значениях a сумма квадратов корней уравнения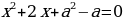 больше чем 12?
больше чем 12?
Решение: Дискриминант уравнения 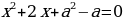 равен 4a. Поэтому действительные корни этого уравнения существуют, если a і 0. Применяя к данному уравнению теорему Виета получаем x1+x2 = 2a и
равен 4a. Поэтому действительные корни этого уравнения существуют, если a і 0. Применяя к данному уравнению теорему Виета получаем x1+x2 = 2a и 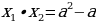 . Отсюда
. Отсюда  . Решениями неравенства
. Решениями неравенства 12, удовлетворяющими условию a і 0, являются числа a 2.
12, удовлетворяющими условию a і 0, являются числа a 2.
Ответ: a 2.
2. Для каждого значения параметра a определите количество решений уравнения |x²-7|x|+6| =а .
Решение:
Заметим, что количество решений уравнения
|x²-7|x|+6| =а .
равно количеству точек пересечения графиков функций
y= |x²-7|x|+6| и y = a.
График функции y=x²-7x+6=(x )²-
)²- 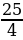 показан на рис.1.
показан на рис.1.
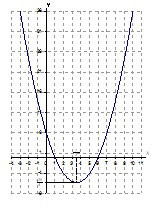
Рис.1
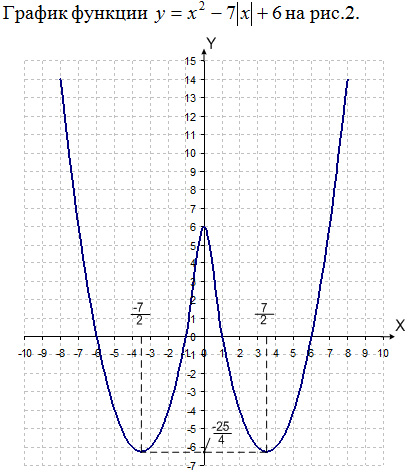
Рис. 2

Рис. 3
y = a – это горизонтальная прямая. По графику несложно установить количество точек пересечения в зависимости от a (например, при a = 11 – две точки пересечения; при a = 2 – восемь точек пересечения).
Ответ: при a a = 0 и a = 25/4 – четыре решения; при 0 a a = 6 – семь решений; при
6 a a 25/4 – два решения.
Метод симметрии.
Довольно часто среди задач с параметрами встречаются такие, в которых требуется единственность решения. В ряде случаев необходимо обратить внимание на внешний вид условия задачи. Различного рода симметрии (симметрия областей значений, областей определения; симметрия относительно переменных) могут значительно упростить поиск искомых значений параметра.
Для решения задач данным методом можно воспользоваться следующим алгоритмом:
1.Изучить условие задачи.
2. Выполнить преобразования.
3. Решить задачу в данном виде.
3.Выбрать достаточное условие для даной задачи .
3. Найти все значения параметра b, при которых уравнение
 имеет единственное решение. [1]
имеет единственное решение. [1]
Решение:
Уравнение не меняет своего вида при замене x на (−x) (ведь x ² и cos x это чётные функции).
не меняет своего вида при замене x на (−x) (ведь x ² и cos x это чётные функции).
Уравнение  симметрично относительно преобразования x → (−x) (по другому относительно отражения в начале координат). Значит, данной симметрией будут обладать и решения данного уравнения. Если x₀ — корень уравнения
симметрично относительно преобразования x → (−x) (по другому относительно отражения в начале координат). Значит, данной симметрией будут обладать и решения данного уравнения. Если x₀ — корень уравнения  , то и число (−x₀) будет его корнем. Однако, условию задачи решение должно быть одно. Соответственно, корнем уравнения
, то и число (−x₀) будет его корнем. Однако, условию задачи решение должно быть одно. Соответственно, корнем уравнения  является ноль. Если уравнение имеет ненулевое решение, то всего решений будет как минимум два.
является ноль. Если уравнение имеет ненулевое решение, то всего решений будет как минимум два.
Подставляя x = 0 в уравнение  , получаем
, получаем
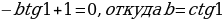 .
.
Это — необходимое условие на b (только при таком b уравнение может иметь нулевое решение).
Является ли это условие достаточным; то есть, окажется ли при b = ctg 1 нулевое решение и в самом деле единственным, или же уравнение  будет иметь и другие корни помимо нуля.
будет иметь и другие корни помимо нуля.
Для выяснения условия достаточности значение b подставляется в уравнение :
:
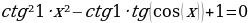

Тангенс является возрастающей функцией на интервале (–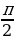 ;
;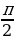 ) . Косинус, являющийся аргументом тангенса, принимает значения из отрезка [−1; 1], а этот отрезок находится внутри интервала (–
) . Косинус, являющийся аргументом тангенса, принимает значения из отрезка [−1; 1], а этот отрезок находится внутри интервала (–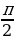 ;
;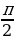 )
)
Тогда, справедливо неравенство tg(cos (x))
Итак, при b = ctg 1 уравнение  имеет единственное (нулевое) решение. Ответ: b = ctg 1.
имеет единственное (нулевое) решение. Ответ: b = ctg 1.
Метод изменения ролей переменных.
Достаточно часто бывает необходимым поменять роли искомой переменной и одного из параметров, чтобы, по крайней мере, получить возможность проведения анализа представленного условия. Достаточно часто бывает, что степень искомой переменной гораздо выше, чем степень входящего в условие параметра. Изменение ролей в этом случае приводит к реальному упрощению процесса решения.
Для решения задач данным методом можно воспользоваться следующим алгоритмом:
1. Выполнить преобразования исходя из условия задачи.
3. Решить задачу в данном виде.
3.вернуться к первоначальному варианту и завершить решение.
4. Указать все значения параметра а , для которых уравнение имеет решение: [4]
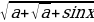 =sinx
=sinx
Sinx = t
│t│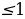
 =t
=t
│t│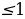
Решение: Обозначим исходное уравнение равносильно системе
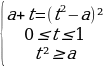

рассмотрим квадратное уравнение относительно параметра, найдём дискриминант данного уравнения :
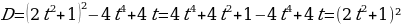 (2
(2
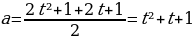 или
или
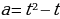
Последняя система равносильна
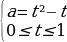
y= t²-t (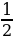
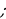
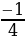 )[
)[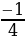 ;0]
;0]
Ответ 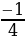
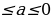
5. При каких значениях параметра 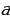 уравнение
уравнение имеет единственный корень?
имеет единственный корень?
Ответ:  ) .
) .
6. При каких значениях параметра 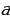 уравнение
уравнение 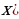 имеет ровно три корня?
имеет ровно три корня?
ответ: .
.
7. При каких 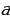 уравнение
уравнение 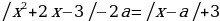 имеет ровно три корня?
имеет ровно три корня?
Ответ: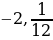 .
.
8. Найдите все значения параметра 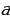 , при каждом из которых система уравнений
, при каждом из которых система уравнений
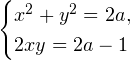
имеет ровно два решения.
ответ:  .
.
9. Найти все значения параметра 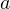 , при которых система
, при которых система

имеет ровно два решения.
ответ: 
10. Найдите все значения 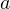 , при каждом из которых уравнение
, при каждом из которых уравнение 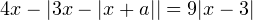 имеет два корня.
имеет два корня.
ответ: 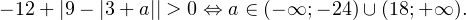







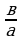 .
.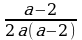 ,
,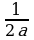 .
. аf(A)или аf(A) 0 (а- старший коэффициент).
аf(A)или аf(A) 0 (а- старший коэффициент).
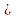 0 (а =
0 (а =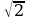 , а =-
, а =- решить уравнение
решить уравнение (1)
(1) 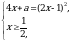
 (2)
(2) 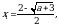
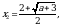 (3)
(3)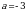 уравнение (1) имеет одно решение
уравнение (1) имеет одно решение  . Если
. Если 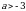 , то
, то  , и тогда уравнение (1) будет иметь два решения при тех значениях параметра
, и тогда уравнение (1) будет иметь два решения при тех значениях параметра  ,
,
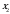 , если
, если 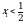 , а
, а  . В этом случае решая систему
. В этом случае решая систему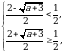
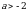 .
. дискриминант уравнения системы (2) отрицателен, получаем
дискриминант уравнения системы (2) отрицателен, получаем ;
; .
.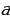 ,
,  является корнем уравнения
является корнем уравнения 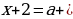 7?
7? 7 , откуда находим
7 , откуда находим 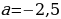 .
.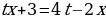
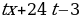
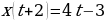
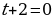 ,
, 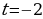 , то уравнение примет следующий вид
, то уравнение примет следующий вид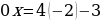 ,
,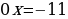 , это уравнение не имеет корней.
, это уравнение не имеет корней.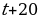 ,
,
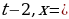
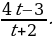
 относительно переменной
относительно переменной 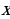 .
.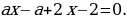
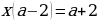 .
. 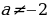 , имеем решение
, имеем решение .
.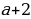 равно нулю, т.е.
равно нулю, т.е. , то имеем равенство
, то имеем равенство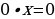 , поэтому
, поэтому ;
;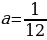
 или
или 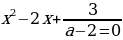
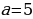
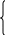 1, если |x|≤ 3
1, если |x|≤ 3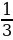 k
k 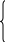 2x2+8x+8, если x
2x2+8x+8, если x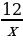 , если x3.
, если x3.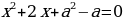 больше чем 12?
больше чем 12? 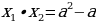 . Отсюда
. Отсюда  . Решениями неравенства
. Решениями неравенства 12, удовлетворяющими условию a і 0, являются числа a 2.
12, удовлетворяющими условию a і 0, являются числа a 2.  )²-
)²- 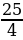 показан на рис.1.
показан на рис.1.


 имеет единственное решение. [1]
имеет единственное решение. [1] 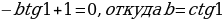 .
. 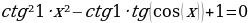

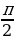 ;
;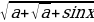 =sinx
=sinx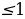
 =t
=t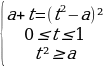

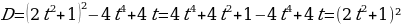 (2
(2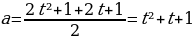 или
или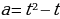
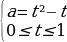
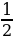
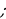
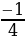 )[
)[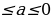
 имеет единственный корень?
имеет единственный корень? ) .
) .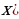 имеет ровно три корня?
имеет ровно три корня? .
.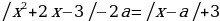 имеет ровно три корня?
имеет ровно три корня?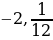 .
.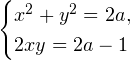
 .
.


















