Презентация по теме "Конус"

Содержание :

• История изучения геометрического тела
• Конус и его элементы
• Усеченный конус. Развертка усеченного конуса.
• Теоремы о площади боковой поверхности конуса и усеченного конуса
• Полная поверхность конуса и усеченного конуса
• Объем конуса
• Объем усеченного конуса
• Вписанные в конус и описанные около него фигуры
• Применение конуса в быту
• Применение конуса в архитектуре
• Нахождение конуса в природе
• Результаты проделанной работы

История изучения геометрического тела ( конуса )

ЕВКЛИД (330-275гг. до н.э.)

В своей XI книге «Начал» дается следующее определение: если вращающийся около одного из своих катетов прямоугольный треугольник слева вернется в то же самое положение, из которого он начал двигаться, то описанная фигура будет конусом.

Неподвижный катет, вокруг которого поворачивается треугольник, называется осью конуса, а круг, описываемый вращающимся катетом, называется основанием конуса. Евклид рассматривает только прямые конусы,

т.е. такие, у которых ось перпендикулярна к основанию, лишь Аполлоний различает прямые и косые конусы, у которых ось образует с основанием угол, отличный от прямого.

В XII книге «Начал» Евклида содержится следующие теоремы.

Объём конуса равен одной трети объёма цилиндра с равным основанием и равной высотой; доказательство этой теоремы принадлежит Евдоксу Книдскому.

Отношение объёмов двух конусов с равными основаниями равно отношению соответствующих высот.

Если два конуса равновелики, то площади их оснований обратно пропорциональны соответствующим высотам и наоборот.

История изучения геометрического тела ( конуса )

Строгое доказательство теорем, служащих для вывода формулы объема конуса и изложенных в пяти предложениях 12 книги “Начал” Евклида, дал ЕВДОКС КНИДСКИЙ. В первом из них методом исчерпывания доказывается, что объем конуса равен 1/3 объема цилиндра, имеющего то же основание и ту же высоту. В следующем предложении тем же методом доказывается, что отношение объемов конусов с равными высотами равно отношению площадей их оснований. В третьем из упомянутых предложений доказывается, что объемы 2 подобных конусов, т. е. таких, у которых оси и диаметры оснований пропорциональны, относятся как кубы диаметров. Наконец, в последних 2 предложениях устанавливается, что отношение объемов 2 конусов, площади оснований которых равны, равно отношению высот. По определению Евклида, конус образуется от вращения прямоугольного треугольника, вокруг одного из катетов.

История изучения геометрического тела ( конуса )

У Евклида нет понятия конической поверхности , оно было введено Аполлонием в его “Конических сечениях”, при этом он имел в виду обе плоскости конуса. Вот что пишет АПОЛЛОНИЙ : «Если от какой-либо точки окружности круга, который не находится в одной плоскости с некоторой точкой, проводить прямые, соединяющие эту точку с окружностью, и при неподвижности точки перемещать прямую по окружности, возвращая ее туда, откуда началось движение, то поверхность, описанную прямой и составленную из 2 поверхностей, лежащих в вершине друг против друга, из которых каждая бесконечно увеличивается, если бесконечно продолжать описывающую прямую, я называю конической поверхностью , неподвижную же точку - её вершиной , а осью - прямую, проведённую через эту точку и центр круга». Определение конической поверхности Аполлония воспроизведено в современных школьных учебниках с существенной заменой круга на любую линию, так называемую направляющую.

История изучения геометрического тела (конуса)

Площадь боковой поверхности была найдена Архимедом . В14-м предложении его произведения «О шаре и цилиндре» он доказал следующую теорему: «Поверхность всякого равнобедренного (т.е. прямого кругового) конуса, за вычетом основания, равна кругу, радиус которого есть средняя пропорциональная между стороной (т.е. образующей) конуса и радиуса круга, являющегося основанием конуса». Площадь S боковой поверхности дается таким образом (в современных символах) формулой S = Pi *( lr )^2= Pirl , где l – длина образующей, r – радиус основания конуса. «Равнобедренным» прямой круговой конус называется потому, что он имел в осевом сечении равнобедренный треугольник.

Конус и его элементы

Прямым круговым конусом называется тело, полученное вращением прямоугольного треугольника вокруг оси, содержащей один из его катетов.

На рисунке 1 вы видите прямоугольный треугольник АОВ, ÐО=90 0 , в результате вращения которого вокруг оси s,содержащей катет АО, получим конус.

Точка А называется вершиной конуса ; круг радиусом ОВ=r с центром в точке О называется основанием конуса , при этом окружность радиуса ОВ с центром в точке О, ограничивающая основание конуса, называется окружностью основания конуса . Отрезок АО=h называется высотой конуса , а прямая, содержащая высоту конуса, называется осью конуса . Ось конуса также как и его высота перпендикулярны основания конуса.

Гипотенуза АВ при своем вращении вокруг оси s образует поверхность, которая называется боковой поверхностью конуса .

Отрезок, один конец которого находится в вершине А конуса, а другой – в некоторой произвольной точке L окружности основания, называется образующей конуса . Все образующие конуса равны между собой.

Конус и его элементы

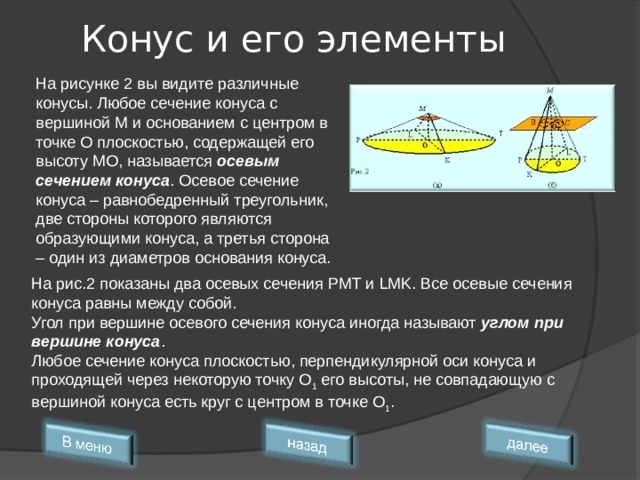
На рисунке 2 вы видите различные конусы. Любое сечение конуса с вершиной М и основанием с центром в точке О плоскостью, содержащей его высоту МО, называется осевым сечением конуса . Осевое сечение конуса – равнобедренный треугольник, две стороны которого являются образующими конуса, а третья сторона – один из диаметров основания конуса.

На рис.2 показаны два осевых сечения PMT и LMK. Все осевые сечения конуса равны между собой.

Угол при вершине осевого сечения конуса иногда называют углом при вершине конуса .

Любое сечение конуса плоскостью, перпендикулярной оси конуса и проходящей через некоторую точку О 1 его высоты, не совпадающую с вершиной конуса есть круг с центром в точке О 1 .

Конус и его элементы

Теорема :

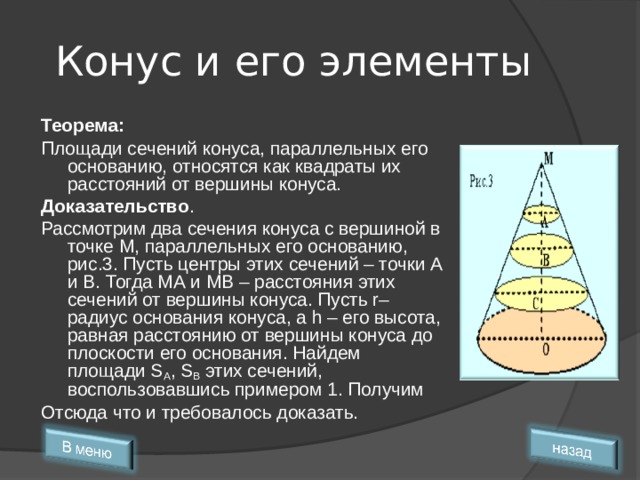
Площади сечений конуса, параллельных его основанию, относятся как квадраты их расстояний от вершины конуса.

Доказательство .

Рассмотрим два сечения конуса с вершиной в точке М, параллельных его основанию, рис.3. Пусть центры этих сечений – точки А и В. Тогда МА и МВ – расстояния этих сечений от вершины конуса. Пусть r– радиус основания конуса, а h – его высота, равная расстоянию от вершины конуса до плоскости его основания. Найдем площади S A , S B этих сечений, воспользовавшись примером 1. Получим

Отсюда что и требовалось доказать.

Усеченный конус. Развертка усеченного конуса.

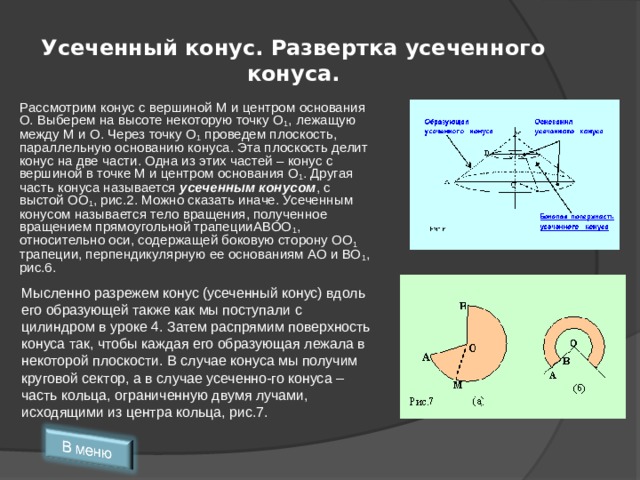
Рассмотрим конус с вершиной М и центром основания О. Выберем на высоте некоторую точку О 1 , лежащую между М и О. Через точку О 1 проведем плоскость, параллельную основанию конуса. Эта плоскость делит конус на две части. Одна из этих частей – конус с вершиной в точке М и центром основания О 1 . Другая часть конуса называется усеченным конусом , с выстой ОО 1 , рис.2. Можно сказать иначе. Усеченным конусом называется тело вращения, полученное вращением прямоугольной трапецииАВОО 1 , относительно оси, содержащей боковую сторону ОО 1 трапеции, перпендикулярную ее основаниям АО и ВО 1 , рис.6.

Мысленно разрежем конус (усеченный конус) вдоль его образующей также как мы поступали с цилиндром в уроке 4. Затем распрямим поверхность конуса так, чтобы каждая его образующая лежала в некоторой плоскости. В случае конуса мы получим круговой сектор, а в случае усеченно-го конуса – часть кольца, ограниченную двумя лучами, исходящими из центра кольца, рис.7.

Теоремы

Теорема 1 :

Площадь боковой поверхности конуса с радиусом основания R и образующей, равной l, может быть найдена по формуле

Теорема 2

Площадь боковой поверхности усеченного конуса с образующей l и радиусами оснований R и R 1 может быть найдена по формуле

Доказательство теоремы о площади боковой поверхности конуса

За площадь боковой поверхности конуса или усеченного конуса принимается площадь развертки конуса или, соответственно, площадь развертки усеченного конуса. Получим соответствующие формулы для площади S K боковой поверхности конуса и площади S УК боковой поверхности усеченного конуса.

Пусть радиус основания конуса равен R, а образующая равна l, рис.7а. Центральный угол, соответствующий дуге АМВ называется углом в развертке конуса . Пусть угол в развертке конуса равен φ. Тогда, по формуле для площади кругового сектора радиусом ОА=l и углом φ получим

Поскольку длина дуги АМВ равна длине окружности основания конуса, то получим

где φ – угол в развертке конуса, выраженный в радианах.

с другой стороны

Имеем равенство

Отсюда

Получим

Таким образом мы доказали теорему о площади боковой поверхности конуса.

Доказательство теоремы о площади боковой поверхности усеченного конуса

Действительно, пусть OA=R; ОВ=R 1 ; AB=l, рис.6 и 7б. Пусть М – точка пересечения образующих усеченного конуса. Тогда М – вершина конуса, из которого получен данный усеченный конус. Следовательно, площадь поверхности усеченного конуса может быть найдена как разность площадей поверхностей двух конусов с общей вершиной М и радиусами оснований R и R 1 . Имеем

Полная поверхность конуса и усеченного конуса

Кроме боковой поверхности конуса и усеченного конуса иногда встречаются понятия полной поверхности конуса и полной поверхности усеченного конуса.

Полной поверхностью конуса называется объединение его боковой поверхности и основания. Поэтому площадь S OK полной поверхности конуса равна сумме площадей основания конуса и боковой поверхности:

Аналогично, полной поверхностью усеченного конуса называется объединение его боковой поверхности и оснований. Поэтому площадь S ОУК полной поверхности усеченного конуса равна сумме площадей оснований усеченного конуса и боковой поверхности:

Объем конуса

Пирамида называется вписанной в конус, если ее основание вписано в основание конуса, а вершина совпадает с основанием конуса.

Объем конуса равен одной трети произведения площади его основания на высоту.

Доказательство.

Впишем в данный конус, радиус основания которого равен R, а высота равна h, правильную n-угольную пирамиду. Объем конуса есть, по определению, предел, к которому стремится объем вписанной правильной n-угольной пирамиды, когда n неограниченно возрастает.

Объем вписанной пирамиды равен одной трети произведения площади ее основания на высоту пирамиды. Последняя будет в то же время и высотой конуса, тогда как площади оснований призм стремятся к площади основания цилиндра. Следовательно, объем конуса

где R – радиус основания цилиндра, а h – его высота

Объем усеченного конуса

Усеченный конус представляется как сумма двух тел вращения, первое из которых получено вращением прямоугольника, со стороной, равной радиуса меньшего основания, а второе – вращением прямоугольного треугольника с катетом, равным разности оснований усеченного конуса.

Центр тяжести прямоугольника удален от оси вращения на расстояние, равное половине длины меньшего основания, т.е. R 1 /2 . Центр тяжести треугольника удален от оси вращения на расстояние, равное R 1 /2 .

По теореме Гюльдена получим, что:

Приводя подобные члены, имеем:

Вписанные в конус и описанные около него фигуры

Конус вписан в сферу (сфера описана около конуса), если его вершина принадлежит сфере, а основание является сечением шара, ограниченного данной сферой (рис. 72, а). Сфера вписана в конус (конус описан около сферы), если сфера касается основания конуса и каждой его образующей (рис. 72,6). Конус вписан в пирамиду (пирамида описана около конуса), если основание конуса вписано в основание пирамиды, а каждая грань пирамиды содержит одну его образующую. На рисунке 73, а изображен конус, вписанный в треугольную пирамиду SABC.

Пирамида вписана в конус (конус описан около пирамиды), если ее основание вписано в основание конуса, а боковые ребра являются образующими конуса. Например, на рисунке 73, 6 изображена четырехугольная пирамида SABCD, вписанная в конус.

Вписанные в конус и описанные около него фигуры

Цилиндр называется вписанным в конус , если одно его основание принадлежит основанию конуса, а второе совпадает с сечением конуса плоскостью, параллельной основанию.

      Основание цилиндра и основание конуса – концентрические круги.

      Во всякий конус можно вписать цилиндр. Его высота меньше высоты конуса.

      Цилиндр называется вписанным в усеченный конус , если одно его основание принадлежит основанию конуса, а другое совпадает со вторым основанием конуса. Высота такого цилиндра равна высоте усеченного конуса.

      Так как цилиндр и конус однозначно определяются двумя независимыми параметрами, то, задав два независимых параметра одной фигуры и один параметр другой (вписанной или описанной), можно найти остальные параметры.

Применение конуса в быту

Знания о конусе широко применяются в жизни - в быту, на производстве, в науке. Например, в быту мы часто используем вёдра, имеющие форму усечённого конуса, служащие нам ёмкостью для различных жидкостей и сыпучих веществ. Наши растения, благоприятно развиваются в цветочных горшках. А эти предметы чаще всего имеют форму либо прямого кругового конуса, либо форму усечённого конуса.

Для переливания жидкостей из более крупной посуды, в более мелкую мы используем воронку. Если присмотреться к её форме, мы заметим, что она похожа на усечённый конус.

Идя по улице, мы можем увидеть человека с интересным приспособлением в руках. Это рупор. Он служит для усиления звука, то есть он является громкоговорителем.

Применение конуса в быту

Многие музыкальные инструменты имеют конические элементы. Например, карнай среднеазиатский, зурна армянская, продольная флейта. А если мы вспомним древнего музыканта, который однажды подул в кость, и превратил её в духовный инструмент. Назовём его флейтой, гобоем, кларнетом, дудкой, фаготом. Это деревянные духовные инструменты. Но есть так же группа медных духовных – валторна, труба, тромбон, туба и их разновидности.

В жизни мы нередко встречаемся с конусами. Лампа с металлическим абажуром отбрасывает пучок света в виде конуса. Причём если абажур не расположен параллельно к земле, то конус не будет являться круговым. Его основание образует вытянутая фигура, называемая эллипсом. Если из круга вырезать сектор, а затем склеить его, получиться конус.

Одной из самых распространённых канцелярских принадлежностей является ручка. Она имеет конический элемент на конце. Этим элементом является зауженный конец ручки.

Применение конуса в архитектуре

При построении различных зданий и сооружений очень требуются познания в области геометрии, а особенно в таком её разделе, как стереометрия. А, в свою очередь, рассматриваемая нами, фигура относится именно к этому разделу.

Очень часто мы встречаем конус в элементах архитектуры. Ярким примером этого наблюдения является конус, который лежит в основании крыш домов

Нахождение конуса в природе

В природе мы часто встречаем конус. Например, в песчаной пустыне Сахаре, где сами холмы представляют собой конус.

А так же в космическом пространстве.

Результаты проделанной работы

При подготовке к этой работе я узнала много нового о геометрической фигуре конус. Например, я стала внимательнее относиться к предметам, окружающим нас в повседневной жизни. Я обнаружила, что вокруг очень много различных геометрических фигур, в том числе и конусы. Они очень широко применяется нами в быту. Так же мы часто сталкиваемся с этой геометрической фигурой в природе. Они широко применяются в промышленности, так как большинство ёмкостей для растворов имеет конусовидную форму.

Если мы пройдёмся по улице какого-либо города, то, наверняка, заметим, что элементы конуса встречаются в архитектуре. Примером этого служат крыши различных зданий и сооружений, где мы с лёгкостью можем увидеть конус.

Так же знания о конусе и его элементов иногда очень требуется в жизни. Например, при подсчёте объёма жидкости, находящейся в ведре, которое имеет форму прямого кругового конуса или усечённого конуса.