Презентация на тему: "Первообразная"

Тема Урока:

Первообразная

Содержание урока:

F'(x) = f(x)

Определение первообразной

F(x)+C = ∫ f(x)dx

Неоднозначность первообразной

Нахождение первообразных в простейших случаях

Проверка первообразной на заданном промежутке

Устные упражнения

C

ln x

sin x

+tg x

а) ( )' = 2x

б) ( )' = 0

в) ( )' =

г) ( )' = cos x

д) ( )' = e x

е) ( )' = x +

Взаимно-обратные операции в математике

Прямая

Обратная

x 2

Возведение в квадрат

Извлечение из корня

sin α = a

Синус угла

arcsin a = α a ∈ [-1;1]

Арксинус числа

(x n )' = nx n-1

Дифференцирование

∫ nx n-1 dx = x n + C

Интегрирование

Пояснение в сравнении

Первообразная

Производная

"Производит" новую ф-ию

Первичный образ

дифференцирование

вычисление производной

интегрирование

восстановление функции из производной

Определение первообразной

y = F(x) называют первообразной для y = f(x) на промежутке X, если при x ∈ X

F'(x) = f(x)

Неоднозначность первообразной

F 1 ' (x) = 2x

F 1 (x) = x 2

F 2 ' (x) = 2x

f(x) = 2x

F 2 (x) = x 2 + 1

F 3 ' (x) = 2x

F 3 (x) = x 2 + 5

y = f(x) имеет бесконечно много первообразных вида y = F(x)+C, где

C - произвольное число

Определение интеграла

Если у функции y = f(x) на промежутке X есть первообразная y = F(x) , то все множества функций вида y = F(x)+C называют

неопределенным интегралом от функции

y = f(x)

Обозначается как ∫ f(x)dx

неопределенный интеграл f (эф) от x (икс) d (дэ) x (икс)

Правила интегрирования

1) F + G первообразная для f + g

2) kF первообразная для kf

3) первообразная для

f(x)

f(x)

F(x)

1

F(x)

1

, n≠1

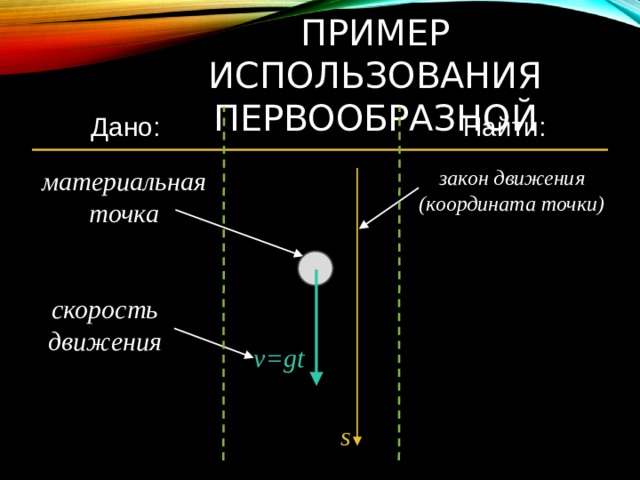
Пример использования первообразной

Найти:

Дано:

закон движения

материальная точка

(координата точки)

скорость

движения

v=gt

s

Пример использования первообразной

Решение:

(s)' = v

v = gt

(s)' = ( + C) ' = gt

s(t) = + C

s(0) = C

s(t) = +

C - координата начала

Отработка материала

Практические задания

Найти одну из первообразных для следующих функций

1) f(x) = 4

1) F(x) = 4x

2) f(x) = -1

2) F(x) = -x

3) f(x) = x 3

3) F(x) =

4) f(x) = sin x

4) F(x) = -cos x

5) f(x) = x 2 + 3cos x

5) F(x) = + 3sin x

Док-ть, что F(x) первообразная для f(x) на заданном промежутке

Доказательство

Условия

Дано: F(x) = 3x 4

Найдем производную F(x) : F'(x) = (3x 4 )' = 12x 3 = f(x)

F'(x) = f(x), значит

Док-ть: f(x) = 12x 3

при x ∈ (-∞;+∞)

F(x) = 3x 4 первообразная для f(x) = 12x 3

Задачи на доказательство:

1) F(x) = ; f(x) = ; x ∈ [0;+∞)

2) F(x) = 2(sin2x) - 3; f(x) = 4cos2x; x ∈ (-∞;+∞)

3) F(x) = ln(-x); f(x) = ; x ∈ (-∞;0)

4) F(x) = ln x; f(x) = ; x ∈ (0;+∞)

Домашнее задание

Теория:

§20, определение наизусть

Практика:

№ 20.1

№ 20.4 (в,г)

№ 20.5 (в,г)