Презентация: "Элементы теории вероятностей"

ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ

достоверное

случайное

невозможное

После 5-го мая наступит 6-е мая.

Вечером пойдет дождь.

Ученику 7 класса 11 месяцев от роду.

невозможное

случайное

случайное

достоверное

Пример 1.

События:

Эксперимент Бросание монеты

4040 2048

12000 6019

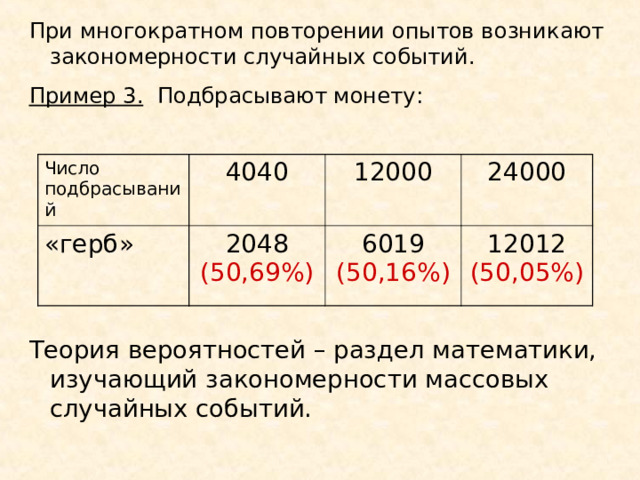
При многократном повторении опытов возникают закономерности случайных событий.

Пример 3. Подбрасывают монету:

Число подбрасываний

4040

«герб»

2048 (50,69%)

12000

24000

6019 (50,16%)

12012 (50,05%)

Теория вероятностей – раздел математики, изучающий закономерности массовых случайных событий.

противоположными

События А и B называются несовместными , если появление события А исключает появление события B .

Например, при бросании игральной кости:

А – выпало более 4 очков,

В – выпало менее 3 очков.

Случайное событие может произойти в результате некоторых условий или действий (эксперимента, опыта).

В результате эксперимента возможно некоторое множество U исходов (элементарных событий) .

Пример 1. Бросают игральную кость.

U={1, 2, 3, 4, 5, 6} , n=6.

Пример 2 . Бросают монету.

U={ герб , решка }, n=2.

Пример 3. Проводится экзамен.

U={“2”, “3”, “4”, “5”}, n=4.

Пример 1. Бросают игральную кость.

Исходы (элементарные события):

U={1, 2, 3, 4, 5, 6} , n=6.

События:

А: “ выпало четное число очков ”.

Благоприятные исходы:

Х= {2, 4, 6} , m=3

B : “ выпало более двух очков ”.

Благоприятные исходы:

Х= { 3 , 4, 5, 6}, m=4.

Классическое определение вероятности

Вероятность P(A) события A :

Формула Лапласа

m – число благоприятных для А событий,

n – общее число исходов

Пример 1. Бросают игральную кость. Исходы: U={1, 2, 3, 4, 5, 6} , n=6.

B : “ выпало более двух очков ”.

Благоприятные исходы:

Х= { 3 , 4, 5, 6}, m=4.

А: “ выпало четное число очков ”.

Благоприятные исходы:

Х= {2, 4, 6} , m=3

Пример 2 . Бросают две монеты.

U={ ГГ , ГР, РГ, РР }, n= 4 .

Г - герб , Р – решка

События:

А: “ обе монеты выпали одной стороной ”.

Благоприятные исходы:

Х= { ГГ , РР } , m= 2.

B : “ первая монета выпала гербом, вторая - решкой ”.

Благоприятные исходы:

Х= { ГР }, m= 1 .

Пример 3. Проводится экзамен.

Исходы (элементарные события):

U={“2”, “3”, “4”, “5”}, n=4.

События:

А: “ экзамен сдан на положительную оценку ”.

Благоприятные исходы:

Х= { “3”, “4”, “5” } , m= 3.

B : “ сдал на “ хорошо ” или “ отлично ” .

Благоприятные исходы:

Х= { “4”, “5” }, m= 2 .

С: “ получил неудовлетворительную оценку .

Благоприятные исходы:

Х= { “ 2 ” }, m= 1 .

ВЕРОЯТНОСТЬ СОБЫТИЙ

Пусть U - исходы (элементарные события):

U={A 1 , A 2 , …, A n },

Каждому событию A i поставим в соответствие число P(A i ) – вероятность элементарного события A i .

P(A 1 ) + P(A 2 ) +…+ P(A n )=1.

Если

P(A 1 ) = P(A 2 ) =…= P(A n )=1 / n,

то A 1 , A 2 , …, A n – равновозможные события

Пример 1. Бросают игральную кость. Вычислить вероятности всех возможных исходов.

Значения суммы очков

1

Вероятности этих значений

2

1/6

3

1/6

4

1/6

5

1/6

6

1/6

1/6

А: “ выпало четное число очков ”.

Благоприятные исходы:

Х= {2, 4, 6} , m=3

P(A) = P(A 2 ) + P(A 4 ) + P(A 6 )= 1/6+ 1/6+ 1/6=3/6=1/2 .

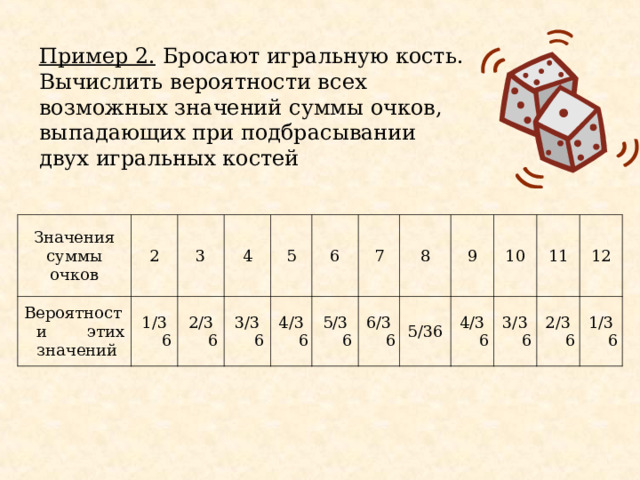
Пример 2. Бросают игральную кость. Вычислить вероятности всех возможных значений суммы очков, выпадающих при подбрасывании двух игральных костей

Значения суммы очков

2

Вероятности этих значений

3

1/36

4

2/36

5

3/36

4/36

6

7

5/36

8

6/36

9

5/36

10

4/36

11

3/36

12

2/36

1/36

СЛОЖЕНИЕ ВЕРОЯТНОСТЕЙ

Суммой (объединением) событий А и В называют событие А+В (А U В), которому благоприятны все исходы, благоприятные хотя бы одному из событий А и В.

Например, при бросании кубика:

А – «выпало более 4 очков» Х= {5,6}

В – «выпало менее 2 очков» Х= {1}

А+В – «выпало более 4 или менее 2 очков» Х= {1,5,6}

СЛОЖЕНИЕ ВЕРОЯТНОСТЕЙ

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:

P(A+B)=P(A)+P(B)

Например,

А – «выпало более 4 очков» Х= {5,6}

P(A)=2/6=1/3

В – «выпало менее 2 очков» Х= {1}

P(B)=1/6

А+В – «выпало более 4 или менее 2 очков» Х= {1,5,6}

P(A+B) = P(A)+P(B) = 1/3+1/6 = 1/2

СЛОЖЕНИЕ ВЕРОЯТНОСТЕЙ

Пример . В урне 10 белых, 15 черных, 20 синих,12 красных шаров. Найти вероятность того, что вынутый шар:

1)белый (А): 2)черный (В): 3)синий (С): 4 )красный ( D ):

5) белый или черный (А+В):

6) красный, синий или черный:

СЛОЖЕНИЕ ВЕРОЯТНОСТЕЙ

Пример . В урне 10 белых, 15 черных, 20 синих,12 красных шаров. Найти вероятность того, что вынутый шар:

1)белый (А): 2)черный (В): 3)синий (С): 4 )красный ( D ):

6) красный, синий или черный:

Заметим:



УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ

Произведением (пересечением) событий А и В называют событие А · В (А ∩ В), которому благоприятны исходы, одновременно благоприятные и событию А и событию В.

Например, при бросании кубика:

А – «выпало более 1 очка» Х= { 2,3,4, 5,6}

В – «выпало менее 5 очков» Х= {1 ,2,3,4 }

А · В – «выпало более 1 и менее 5 очков» Х= { 2,3 , 4 }

УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ

Вероятность произведения двух независимых событий равна произведению вероятностей этих событий:

P(A · B)=P(A) · P(B)

Например, бросаем кубик два раза:

А – «в первый раз выпало более 4 очков» Х= {5,6}

P(A)=2/6=1/3

В – «во второй раз выпало менее 2 очков» Х= {1}

P(B)=1/6

А · В – «в первый раз выпало более 4 , а во второй - менее 2 очков» Х= {5,6} × {1} = { (5, 1 ) , (6 , 1) }

P(A · B)=P(A) · P(B) = 1/3 × 1/6 = 1/ 18

УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ

Пример . В урне 10 белых и 15 черных шаров. Вынимают один шар, затем возвращают его в урну и вынимают шар еще раз. Найти вероятность того, что:

1) первый шар – белый, второй – черный.

первый шар – белый, второй – черный:

Обозначим события:

А: первый шар – белый, В: первый шар – черный,

С: второй шар – белый, D : второй шар – черный,

УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ

Пример . В урне 10 белых и 15 черных шаров. Вынимают один шар, затем возвращают его в урну и вынимают еще раз шар. Найти вероятность того, что:

2) оба шара - белые:

А: первый шар – белый, В: первый шар – черный,

С: второй шар – белый, D : второй шар – черный.

3) шары разного цвета:

СЛОЖЕНИЕ И УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ

Задача 1. Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания в цель для первого, второго и третьего стрелков равна 0.75, 0.8, 0.9. Определить вероятность того, что

1)одновременно три стрелка попадут в цель:

2)все стрелки промахнутся:

СЛОЖЕНИЕ И УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ

Задача 2 . В ящике лежат шары: 4 белых, 10 красных, 8 зеленых, 9 коричневых. Из ящика вынимают один шар. Определить, какова вероятность, что шар окажется цветным (не белым)?

Задача 3. В вопросах к зачету имеются 75% вопросов, на которые студенты знают ответы. Преподаватель выбирает из них два вопроса и задает их студенту. Определить вероятность того, что среди полученных студентом вопросов есть хотя бы один, на который он знает ответ.

Источники

• Виленкин Н.Я. и др. Алгебра и математический анализ для 11 кл.: Учеб.пособие для классов с углубл. изуч. курса математики. М.:Просвещение, 1990.
• Студенецкая В.Н. и др. Математика. 10-11 классы: элективный курс «В мире закономерных случайностей». Волгоград: Учитель, 2007.
• Бунимович Е. А., Булычев В. А. Вероятность и статистика в курсе математики общеобразовательной школы. - М.: Педагогический университет «Первое сентября», 2005.
• Бунимович Е. А., Булычев В. А. Учебное пособие для 5-9 классов общеобразовательных учреждений. - М.: Дрофа, 2002.
• Лютикас В. С. Факультативный курс по математике. Теория вероятностей. - М.: Просвещение, 1990.