Практическое занятие
Тема: «Производная и ее приложения».
Наименование работы: «Вычисление производных высших порядков, обратной функции и частных производных функции нескольких переменных».
Цель: формирование умений вычислять производные высших порядков, обратной функции и частных производных функции нескольких переменных
Содержание
Часть 1. Теоретическая
Производные высших порядков
Производная f '(х) от функции f(х) называется также производной первого порядка. В свою очередь производная от функции f '(х) называется производной второго порядка от функции f(х) и обозначается f ''(х). Аналогично определяется производная третьего порядка, обозначаема f '''(х) и так далее, производная n-го порядка обозначается f(n)(х).
Понятие дифференциала
Пусть функция у=f(х) определена в некоторой окрестности точки х0. Тогда если существует такое число А, что приращению ∆у этой функции в точке х0, соответствующее приращение ∆х аргумента, представимо в виде:
∆у=А∙∆х + L(∆х)∙∆х,
где lim L (∆х) = 0, то функция f(х) называется дифференцируемой в
∆х→0
точке х0. При этом главная, линейная относительно ∆х, часть этого приращения, т.е. А∙ ∆х, называется дифференциалом функции в точке х0 и обозначается dy или df (х0).
Пример. Найти производные функций.
1) f(х) = 2х5+3х+6;
f '(х)'=(2х5+3х+6)'=(2х5)'+(3х)'+(6)'=10х4+3.
2) f(х) = ℓ2+4х;
f(х)'=(ℓ2+4х)'=(ℓ2)'+(4х)'=0+4х ∙ ln 4=4х ln4.
3) f(х)=2х ∙ х4;
f '(х)=( 2х ∙ х4)'=(2х)' ∙ х4 + 2х ∙ (х4)' = 2х ln 2 ∙ х4 +2х ∙ 4х3 = 2хх3 (х ln 2+4).
4) f(х) = 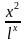 ;
;
f '(х) =(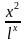 )=
)=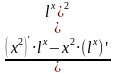 =
=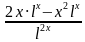 =
=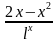 .
.
5) f(х)=5sin х + log 6х;
f '(х) = (5sin х - log 6х)'=(5sin х)' – (log 6х)= 5 cos х - 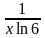 .
.
6) f(х)=(2-х3)5;
f '(х) =((2-х3)5)'=5∙(2-х3)4 ∙ (2-х3)'=5∙(2-х3)4 ∙(-3х2)=-15х2∙(2-х3)4.
7) f(х)=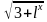 ;
;
f '(х)=(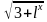 )'=
)'=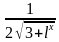 ∙ (
∙ (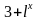 )'=
)'=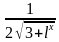 ∙
∙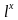 =
=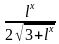 .
.
Пример. Найти производные функций при заданном значении аргумента.
1) f (х) = 2х3-5х2+4, у'(2);
f '(х) = 2∙3х2 - 5∙2х = 6х2 – 10х; у'(2) = 6∙22 -10∙2 = 6∙4 – 20=4.
2) f (х) = 2ℓх + 3 cosх, у'(0);
f '(х) = 2ℓх + 3∙ (- sin х) = 2ℓх - 3 sin х; у'(0)= 2ℓ0 - 3 sin 0 = 2∙1 - 3∙0=2.
Пример. Найти производные указанных порядков для заданных функций.
f (х) = sin 3 х, f'''(х);
f '(х) = (sin 3 х)' = 3cos 3х; f''(х)= (3cos 3х)' = -9 sin 3 х;
f'''(х) = (- 9 sin 3 х)' = -27cos 3х.
Пример. Найти дифференциал функции.
f (х) =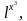 df(х); так как df(х) = f '(х) dх, то в нашем случае
df(х); так как df(х) = f '(х) dх, то в нашем случае
df(х) = (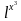 ) dх=3х2
) dх=3х2 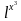 dх.
dх.
Обратная функция.
Пусть функция 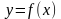 непрерывна и строго монотонна в некоторой окрестности точки
непрерывна и строго монотонна в некоторой окрестности точки 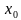 , и пусть в этой точке существует производная
, и пусть в этой точке существует производная 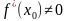 . Тогда обратная функция в точке имеет производную, которая может быть найдена по формуле(
. Тогда обратная функция в точке имеет производную, которая может быть найдена по формуле( 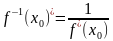 .
.
Функции нескольких переменных
Если каждой паре значений переменных х и у (из некоторого множества) соответствует одно и только одно число z (действительное), то z называют функцией двух переменных.
Обозначение: z = f(x,y), где x,y – аргументы.
Аналогично для определения функции трех и более переменных.
Обозначение: u = f(x,y, z).
Частной производной функции Z = f(x,y) по переменной х называется выражение: Z 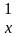 =
= 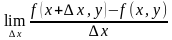 =
= 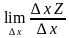 .
.
Обозначение: 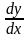 ,
, 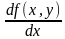 ,
,  х(х,у).
х(х,у).
Аналогично определяется и обозначается частная производная по переменной у.
Частные производные от функции нескольких переменных являются также функциями нескольких переменных, для которых можно найти частные производные, которые называются частными производными высшего порядка.
Пример.
Найти частные производные для функции Z =  .
.
Решение.  = 2х
= 2х ,
,  =
=  ,
,  = 2
= 2 ,
,  = -
= -  ,
,
 = 2х
= 2х .
.
Пример.
Найти частные производные для функции Z = 
Решение.  = 4 = 2
= 4 = 2 ,
,  = 12
= 12
 = 2
= 2
 = 6
= 6
Часть 2. Практическая.
Задание 1. Найти производные второго и третьего порядков, обратной функции для следующих функций:
| № | Задание | № | Задание |
| 1 | 
| 6 | 
|
| 2 | 
| 7 | 
|
| 3 | | 8 | 
|
| 4 | 
| 9 | 
|
| 5 | | 10 | 
|
Задание 2. Найти частные производные от функции, градиент и полный дифференциал функции:
| № | Задание | № | Задание |
| 1 | u= | 6 | |
| 2 | | 7 | 
|
| 3 | 
| 8 | 
|
| 4 | 
| 9 | |
| 5 | 
| 10 | |
Вопросы к практическому занятию
Что называется производной n-ого порядка?
Что называется дифференциалом функции в точке
Как обозначается дифференциал функции?
Что называется функцией нескольких переменных?
Что называется производной функции Z = f(x,y) по переменной х?
Что называется производной функции Z = f(x,y) по переменной y?







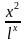 ;
;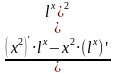 =
=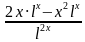 =
=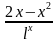 .
.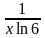 .
.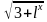 ;
;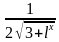 ∙ (
∙ (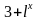 )'=
)'=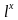 =
=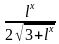 .
.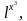 df(х); так как df(х) = f '(х) dх, то в нашем случае
df(х); так как df(х) = f '(х) dх, то в нашем случае 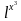 ) dх=3х2
) dх=3х2 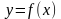 непрерывна и строго монотонна в некоторой окрестности точки
непрерывна и строго монотонна в некоторой окрестности точки 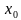 , и пусть в этой точке существует производная
, и пусть в этой точке существует производная 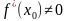 . Тогда обратная функция в точке имеет производную, которая может быть найдена по формуле(
. Тогда обратная функция в точке имеет производную, которая может быть найдена по формуле( 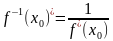 .
.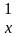 =
= 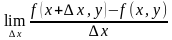 =
= 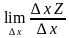 .
.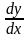 ,
, 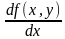 ,
, 

















