Практическое занятие
Тема: «Математический анализ».
Наименование работы: «Вычисление неопределенных интегралов различными методами».
Цель: Закрепить навыки интегрирования рациональных функций, интегрирования методом замены переменной и интегрирования по частям.
Содержание
Часть 1. Теоретическая
Интегрирование - это действие, обратное дифференцированию. С помощью интегрирования по данной производной или дифференциалу функций находится сама функция.
Дифференцируемая функция F(x), a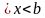 называется первообразной для функции f(x) на интервале a
называется первообразной для функции f(x) на интервале a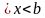 , если
, если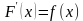 для каждого a
для каждого a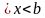 .
.
Так, для функции f(x) = cosx первообразной служит функция F(x) = sinx, поскольку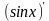 = cosx.
= cosx.
Для заданной функции ее первообразная определяется неоднозначно. Если F(x) – первообразная для f(x) на некотором промежутке, то и функция F(x) + C, где C – любая постоянная, также является первообразной для функции f(x) на этом промежутке. Обратно: каждая функция, являющаяся первообразной для f(x) в данном промежутке, может быть записана в виде F(x) + C.
Совокупность F(x) + Cвсех первообразных функции f(x) на интервале a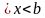 называют неопределенным интегралом от функции f(x) на этом интервале и пишут
называют неопределенным интегралом от функции f(x) на этом интервале и пишут 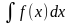 = F(x) + C. Здесь
= F(x) + C. Здесь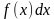 – подынтегральное выражение; f(x) – подынтегральная функция; x – переменная интегрирования; C – произвольная постоянная.
– подынтегральное выражение; f(x) – подынтегральная функция; x – переменная интегрирования; C – произвольная постоянная.
Пример:
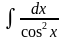 =tgx + C, так как
=tgx + C, так как 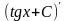 =
= 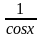 .
.
Если функция f(x) имеет на некотором промежутке хотя бы одну первообразную, то ее называют интегрируемой на этом промежутке. Можно доказать, что любая функция, непрерывная на отрезке a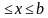 , интегрируема на этом отрезке.
, интегрируема на этом отрезке.
Свойства неопределенного интеграла
1.Дифференциал неопределенного интеграла равен подынтегральному выражению:
d ∫ f(x)dx=f(x) dx.
2.Неопределенный интеграл от дифференциала функции равен этой функции, сложной с произвольной постоянной, т. е.
∫dF(x)=F(x)+C.
3.Постоянный множитель можно выносить за знак неопределенного интеграла:
∫af(x)dx=a∫(x)dx.
4.Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме неопределенных интегралов от каждой функции:
∫(f1(x)±f2(x))dx=∫f1(x)dx±∫f2(x)dx.
Способы интегрирования
Под непосредственным интегрированием понимают такой способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.
Основные формулы интегрирования (табличные интегралы)
1.∫dx=x+C/
2.∫xndx=(xn+1/n+1)+C (n≠-1).
3.∫x-1dx=∫dx/x=ln׀x׀+C.
4.∫exdx=ex+C.
5.∫axdx=ax/lna+C.
6.∫sinxdx=-cosx+C.
7.∫cosxdx=sinx+C.
8.∫dx/cos2x = tgx+C.
9.∫dx/sin2x = -ctgx+C.
10.∫dx/√1-x2 = arcsinx+C.
11.∫dx/1+x2 = arctgx+C.
Если интеграл затруднительно привести к табличному с помощью элементарных преобразований, то в этом случае пользуются методом подстановки.
Пример.
Найти∫xdx/√2-3x2.
Решение. Проведем подстановку 2-3x2=t; тогда -6xdx=dt, xdx=-(1/6)dt. Далее, получаем∫xdx/√2-3x2=∫-(1/6)dt/√t=-1/6∫t-1/2dt=-1/6∙t-1/2+1/(-1/2+1)+C=-1/6∙t1/2/1/2+C=-1/3√t+C=-1/3√2-3x2+C.
Пример.
Найти ∫(2+cosx)2sinxdx.
Решение. Сначала положим 2+cosx=t; тогда –sinxdx=dt,откуда sinxdx=-dt. Далее, получаем
∫(2+cosx)2sinxdx=∫t2(-dt)=-∫t2dt=-t2+1/(2+1)+C=-1/3t3+C=-1/3(2+cosx)3+C.
Пример.
Найти ∫sin10xdx.
Решение. Положим 10x=t;тогда10dx=dt, откуда dt=(1/10)dt. Далее получаем
∫sin10xdx=∫sint1/10dt=1/10∫sintdt=1/10(-cost)+C=-1/10cost+C=-1/10cos10x+C.
В практике интегрирования часто встречаются интегралы, для нахождения которых можно использовать следующие формулы (k≠0, n≠0-постоянные):
1.∫ekxdx=(1/k)ekx+C.
2.∫akxdx=(1/k)(akx/lna+C.
3.∫sinkxdx=(-1/k)coskx+C.
4.∫coskxdx=(1/k)sinkx+C.
5.∫dx/cos2kx=(1/k)tgkx+C.
6.∫dx/sin2kx=(-1/k)ctgkx+C.
7.∫dx/k2+n2x2=(1/nk)arctg (n/k)x+C.
8∫dx/√k2-n2x2=(1/n)arcsin(n/k)x+C.
Так, при вычислении ∫sin10xdx можно использовать формулу ∫sinkxdx=-(1/k)coskx+C, где k=10. Тогда ∫sin10xdx=(-1/10)cos10x+C.
Интегрирование по частям. Общая формула интегрирования по частям имеет вид: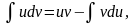 где
где 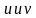 – некоторые функции от х.
– некоторые функции от х.
Пример.
Вычислить интеграл 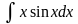 .
.
Решение. Обозначим х = 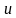 ,
, 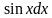 =
= 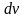 , находим
, находим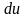 и
и 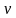 .
. 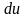 =
= 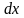 ,
,
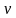 =
= 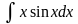 = -
= - 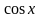 , найдем
, найдем 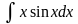 = -х
= -х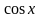 +
+  = -х
= -х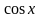 +
+  + С.
+ С.
Часть 2. Практическая
| № | Задание |
| 1 | , ,  , , |
| 2 | , ,  , , |
| 3 | , ,  , , |
| 4 | , ,  , , |
| 5 | , ,  , , |
| 6 | , ,  , , |
| 7 | , ,  , ,  |
| 8 | , ,  , ,  |
| 9 | , ,  , , |
| 10 |  , , , ,  , , 
|
Вопросы к практическому занятию
1.Какое действие называется интегрированием?
2.Какая функция называется первообразной для функции f(x)?
3.Дайте определение неопределенного интеграла?
4.Перечислите основные свойства неопределенного интеграла.
5.Каким действием можно проверить интегрирование?
6.Напишите основные формулы интегрирования (табличные интегралы).







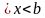 называется первообразной для функции f(x) на интервале a
называется первообразной для функции f(x) на интервале a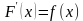 для каждого a
для каждого a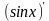 = cosx.
= cosx.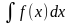 = F(x) + C. Здесь
= F(x) + C. Здесь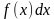 – подынтегральное выражение; f(x) – подынтегральная функция; x – переменная интегрирования; C – произвольная постоянная.
– подынтегральное выражение; f(x) – подынтегральная функция; x – переменная интегрирования; C – произвольная постоянная.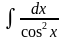 =tgx + C, так как
=tgx + C, так как 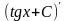 =
= 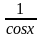 .
.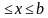 , интегрируема на этом отрезке.
, интегрируема на этом отрезке.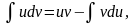 где
где 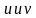 – некоторые функции от х.
– некоторые функции от х.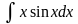 .
.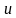 ,
, 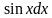 =
= 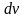 , находим
, находим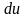 и
и 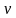 .
. 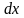 ,
,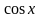 , найдем
, найдем 


















