Практическое занятие
Тема: «Математический анализ».
Наименование работы: «Техника вычисления определенных интегралов».
Цель: научиться вычислять определенные интегралы, используя непосредственное интегрирование, метод подстановки, интегрирование по частям.
Содержание
Часть 1. Теоретическая
Пусть функция f(x) определена на отрезке a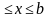 . Допустим, что функция f(x) в указанном промежутке неотрицательна и a
. Допустим, что функция f(x) в указанном промежутке неотрицательна и a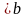 . Разобьем этот отрезок на nчастей точками a =
. Разобьем этот отрезок на nчастей точками a = 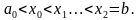 На каждом из частичных отрезков
На каждом из частичных отрезков 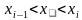 (i = 1, 2, 3, …, n) возьмем произвольную точку
(i = 1, 2, 3, …, n) возьмем произвольную точку 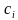 и составим сумму: f(
и составим сумму: f(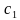 )
)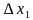 + f(
+ f(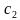 )
)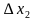 + f(
+ f(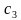 )
)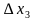 + … + f(
+ … + f(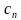 )
)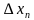 =
= 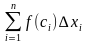 , где
, где 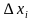 =
= 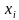 -
- 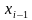 . Эта сумма носит название интегральной суммы функции f(x) на отрезке a
. Эта сумма носит название интегральной суммы функции f(x) на отрезке a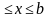 .
.
Геометрически каждое слагаемое интегральной суммы равно площади прямоугольника с основанием 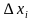 и высотой
и высотой 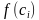 , а вся сумма равна площади «ступенчатой фигуры», получающейся объединением всех указанных выше прямоугольников.
, а вся сумма равна площади «ступенчатой фигуры», получающейся объединением всех указанных выше прямоугольников.
Будем увеличивать число точек разбиения так, чтобы длина наибольшего из отрезков 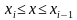 стремилась к нулю. Во многих случаях при таком разбиении интегральная сумма будет стремиться к некоторому конечному пределу, не зависящему ни от способа, каким выбираются точки деления
стремилась к нулю. Во многих случаях при таком разбиении интегральная сумма будет стремиться к некоторому конечному пределу, не зависящему ни от способа, каким выбираются точки деления 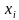 , ни от того, как выбираются промежуточные точки
, ни от того, как выбираются промежуточные точки 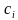 .
.
Определенным интегралом от функции f(x) на отрезке a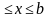 называется предел, к которому стремится интегральная сумма при стремлении к нулю длины наибольшего частичного интервала. Он обозначается символом
называется предел, к которому стремится интегральная сумма при стремлении к нулю длины наибольшего частичного интервала. Он обозначается символом 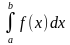 и читается «интеграл от aдо bот функции f(x)по
и читается «интеграл от aдо bот функции f(x)по ».
».
По определению, 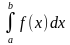 = .
= .
Числоaназывается нижним пределом интегрирования, число  – верхним; отрезок a
– верхним; отрезок a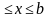 – отрезком интегрирования.
– отрезком интегрирования.
Всякая непрерывная на отрезке a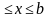 функцияf(x) интегрируема на этом отрезке.
функцияf(x) интегрируема на этом отрезке.
Если интегрируемая на отрезке a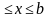 функцияf(x)неотрицательна, то определенный интеграл
функцияf(x)неотрицательна, то определенный интеграл 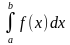 численно равен площади Sкриволинейной трапеции, ограниченной графиком функции у =f(x), осью абсцисс и прямымиx = a, x= b, то есть S =
численно равен площади Sкриволинейной трапеции, ограниченной графиком функции у =f(x), осью абсцисс и прямымиx = a, x= b, то есть S = 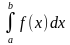 . В этом заключается геометрический смысл определенного интеграла.
. В этом заключается геометрический смысл определенного интеграла.
Основные свойства определённого интеграла
Определенный интеграл с одинаковыми пределами равен нулю:
 = 0.
= 0.
При перестановке пределов интегрирования знак интеграла меняется на противоположный:
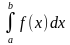 = -
= -  .
.
Отрезок интегрирования можно разбивать на части:
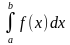 =
=  +
+  .
.
Постоянный множитель можно выносить за знак интеграла:
= с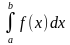 .
.
Интеграл от алгебраической суммы функций равен сумме интегралов от всех слагаемых:
=  +
+
Способы интегрирования
Непосредственное вычисление определенного интеграла. Для вычисления неопределенного интеграла, когда можно найти соответствующий неопределенный интеграл, служит формула Ньютона – Лейбница
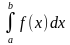 =
=  |
| = F
= F = F(b) – F(a),
= F(b) – F(a),
то есть определенный интеграл равен разности значений любой преобразованной функции при верхнем и нижнем пределах интегрирования.
Из этой формулы виден порядок вычисления определенного интеграла:
найти неопределенный интеграл от данной функции;
в полученную первообразную подставить вместо аргумента сначала верхний, затем нижний пределы интегрирования;
из результата подстановки верхнего предела вычесть результат подстановки нижнего предела.
Пример.
Вычислить интеграл òdx/3Öx2.
Решение. Воспользуемся определением степени с дробным и отрицательным показателем и вычислим определённый интеграл:
 =
=  =
=  = 3
= 3 = 3(
= 3( )=3(2-1)=3.
)=3(2-1)=3.
Пример.
Вычислить интеграл 
Решение. Применив указанное правило, вычислим данный определенный интеграл: =
=  |
| =
=
Часть 2. Практическая
| № | Задание |
| 1 |  |
| 2 | |
| 3 | , |
| 4 | |
| 5 | , ,  |
| 6 | , |
| 7 |  , , , , |
| 8 |  |
| 9 | |
| 10 | |
Вопросы к практическому занятию
Дайте определение определенного интеграла.
Укажите геометрический смысл определенного интеграла.
Перечислите основные свойства определенного интеграла.
Запишите формулу Ньютона-Лейбница.
Перечислите основные методы интегрирования.







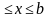 . Допустим, что функция f(x) в указанном промежутке неотрицательна и a
. Допустим, что функция f(x) в указанном промежутке неотрицательна и a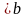 . Разобьем этот отрезок на nчастей точками a =
. Разобьем этот отрезок на nчастей точками a = 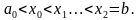 На каждом из частичных отрезков
На каждом из частичных отрезков 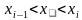 (i = 1, 2, 3, …, n) возьмем произвольную точку
(i = 1, 2, 3, …, n) возьмем произвольную точку 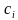 и составим сумму: f(
и составим сумму: f(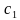 )
)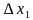 + f(
+ f(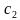 )
)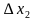 + f(
+ f(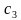 )
)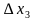 + … + f(
+ … + f(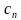 )
)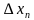 =
= 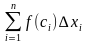 , где
, где 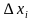 =
= 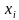 -
- 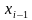 . Эта сумма носит название интегральной суммы функции f(x) на отрезке a
. Эта сумма носит название интегральной суммы функции f(x) на отрезке a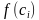 , а вся сумма равна площади «ступенчатой фигуры», получающейся объединением всех указанных выше прямоугольников.
, а вся сумма равна площади «ступенчатой фигуры», получающейся объединением всех указанных выше прямоугольников.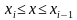 стремилась к нулю. Во многих случаях при таком разбиении интегральная сумма будет стремиться к некоторому конечному пределу, не зависящему ни от способа, каким выбираются точки деления
стремилась к нулю. Во многих случаях при таком разбиении интегральная сумма будет стремиться к некоторому конечному пределу, не зависящему ни от способа, каким выбираются точки деления 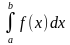 и читается «интеграл от aдо bот функции f(x)по
и читается «интеграл от aдо bот функции f(x)по
















