Просмотр содержимого документа
«Практическое занятие «Применение определенного интеграла».»
Практическое занятие
Тема: «Математический анализ».
Наименование работы: «Применения определенного интеграла».
Цель: научиться определять форму полученной фигуры в сравнении с криволинейной трапецией, аналитически выражать и вычислять площадь полученной фигуры.
Содержание
Часть 1. Теоретическая
Пример.
Вычислить площадь земельного участка, если на плоскости он ограничен линиями: у = 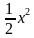 + 1; у = 0; х = -2; х = 3.
+ 1; у = 0; х = -2; х = 3.
Решение.S = 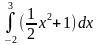 = (
= (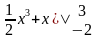 = (
= (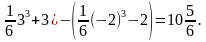
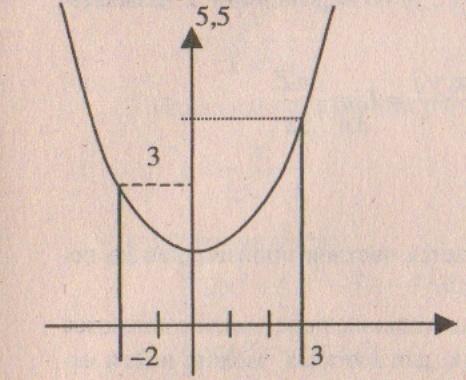
Таким образом, площадь земельного участка составляет 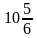 единиц.
единиц.
Пример.
Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями 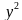 = 4х; у = 0; х = 0; х = 4.
= 4х; у = 0; х = 0; х = 4.
Решение.V =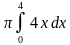 = 2
= 2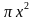 |
|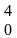 = 32
= 32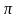 . В решении использована формула V =
. В решении использована формула V =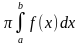 .
.
Пример.
Вычислить массу стержня, расположенного на отрезке 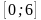 , если плотность задается функцией p(x) = 2
, если плотность задается функцией p(x) = 2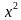 + 3.
+ 3.
Решение. Используем формулу m = 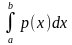 , где
, где 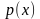 - плотность стержня.
- плотность стержня.
m = 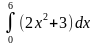 = (
= (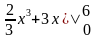 =
= 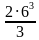 + 3
+ 3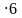 = 162.
= 162.
Часть 2. Практическая
Задание 1. Воспользовавшись соответствующим приложением определенного интеграла к задачам геометрии, найти площадь фигуры, ограниченной линиями:
| № | Задание | № | Задание |
| 1 | y = 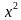 , y = 7x – 12 , y = 7x – 12 | 6 | y = lnx, y = 1 y = 4 |
| 2 | y = 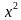 , y = , y = 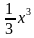 | 7 | y = 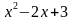 , y = 3x - 1 , y = 3x - 1 |
| 3 | y = lnx, x = 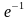 , x = e , x = e | 8 | y =  , y = x , y = x |
| 4 | y =  , x = 0, x = e , x = 0, x = e | 9 | y = -  , y = -9x , y = -9x |
| 5 | y = 9 - 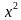 , y = 0 , y = 0 | 10 | y = 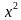 , y = , y =  |
Задание 2. Решите задачу.
| № | Задание | № | Задание |
| 1 | Скорость движения точки определяется по закону v= . Найдите путь S, пройденный точкой за 3-ю секунду . Найдите путь S, пройденный точкой за 3-ю секунду | 6 | Скорость движения точки определяется по закону v= . Найдите путь S, . Найдите путь S, пройденный точкой за 2-ю секунду |
| 2 | Скорость движения точки определяется по закону v= . Найдите путь S, пройденный точкой за 4-ю секунду . Найдите путь S, пройденный точкой за 4-ю секунду | 7 | Скорость движения точки определяется по закону v= . Найдите . Найдите путь S, пройденный точкой за 10-ю секунду |
| 3 | Скорость движения точки определяется по закону v= . Найдите путь S, пройденный точкой за 4-ю секунду . Найдите путь S, пройденный точкой за 4-ю секунду | 8 | Скорость движения точки определяется по закону v= . Найдите путь S, . Найдите путь S, пройденный точкой за 4-ю секунду |
| 4 | Скорость движения точки определяется по закону v= . Найдите путь S, пройденный точкой за 2-ю секунду . Найдите путь S, пройденный точкой за 2-ю секунду | 9 | Скорость движения точки определяется по закону v= . Найдите путь S, . Найдите путь S, пройденный точкой за 4-ю секунду |
| 5 | Скорость движения точки определяется по закону v= . Найдите путь S, пройденный точкой за 3-ю секунду . Найдите путь S, пройденный точкой за 3-ю секунду | 10 | Скорость движения точки определяется по закону v= . Найдите путь S, . Найдите путь S, пройденный точкой за 4-ю секунду |
Задание 3. Найдите объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями. Сделайте чертеж.
| № | Задание | № | Задание |
| 1 | у=  , у=0, х=9 , у=0, х=9 | 6 | у=х+1, х=0, х=2, у=0 |
| 2 | у=2+х, х=1, х=2, у=0 | 7 | у=3х, х=2, у=0 |
| 3 | у=2х, х=1, х=4, у=0 | 8 | у=  , у=0, х=1, х=4 , у=0, х=1, х=4 |
| 4 | у=2-х, х=0, у=0 | 9 | у= 2х, х=3, у=0 |
| 5 | у=х, х=5, у=0 | 10 | у= , у=0, х=4 , у=0, х=4 |
Вопросы к практическому занятию
Сформулируйте определение криволинейной трапеции.
Сформулируйте определение первообразной.
Сколько первообразных может иметь каждая функция?
Каков алгоритм вычисления площади криволинейной трапеции?
Какие известны правила вычисления первообразных?
По какой формуле вычисляется площадь криволинейной трапеции?
Перечислите виды задач, решаемые с помощью определенного интеграла.







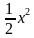 + 1; у = 0; х = -2; х = 3.
+ 1; у = 0; х = -2; х = 3.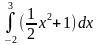 = (
= (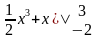 = (
= (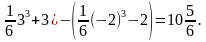
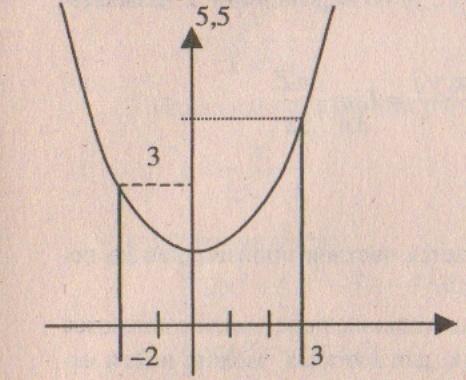
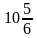 единиц.
единиц.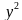 = 4х; у = 0; х = 0; х = 4.
= 4х; у = 0; х = 0; х = 4.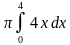 = 2
= 2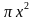 |
|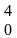 = 32
= 32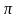 . В решении использована формула V =
. В решении использована формула V =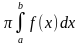 .
.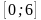 , если плотность задается функцией p(x) = 2
, если плотность задается функцией p(x) = 2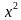 + 3.
+ 3.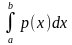 , где
, где 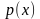 - плотность стержня.
- плотность стержня. 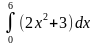 = (
= (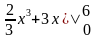 =
= 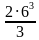 + 3
+ 3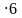 = 162.
= 162.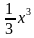
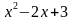 , y = 3x - 1
, y = 3x - 1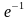 , x = e
, x = e
















